Задача про стеклянные шары — решение в общем случае

Задача про стоэтажный дом и два стеклянных шара давно будоражит интернет-сообщество (Хабрахабр, ЖЖ, форумы). Пытливые умы непременно задаются вопросом: что делать в общем случае, когда у нас n этажей и k шаров?

Скажем, сколько бросков (хотя бы примерно), потребуется в случае n = 2⁴⁰, k = 10?

Объединив найденные на просторах сети сведения и собственные наработки, хочу представить вам пост о ключевых идеях решения этой задачи, а также об основных результатах и интересных наблюдениях, полученных в ходе исследования.

Итак, сформулируем условие: у нас есть k одинаковых стеклянных шаров. При падении с «x»-го или более высокого этажа «n»-этажного дома они разбиваются, при падении с «x – 1»-го или более низкого этажа – остаются целыми. Значение x неизвестно и может быть любым натуральным числом от 1 до n. Требуется:
1. Определить наименьшее число испытаний (бросков шара), за которое можно гарантированно найти x (вне зависимости от его значения, в худшем для нас случае).
2. Разработать алгоритм, позволяющий гарантированно найти x за не более чем указанное выше число испытаний.

Грубая оценка наименьшего числа испытаний

Легко выделить два крайних случая:
А) у нас только 1 шар. Тогда мы вынуждены бросать его по очереди с каждого этажа, начиная с первого, пока он не разобьется или пока мы не дойдем до «n – 1»-го этажа. Если шар разбился на «a»-ом этаже (1 ≤ a ≤ n – 1), то x = a. Если не разбился на «n – 1»-ом, то x = n. В худшем случае понадобится n – 1 испытание.
Б) у нас много шаров (а именно, k ≥ log₂n). Тогда можно применить

В худшем случае понадобится ⌈log₂n⌉ испытаний и такое же количество шаров (вдруг они каждый бросок будут разбиваться).

Таким образом, наименьшее число испытаний находится в диапазоне от ⌈log₂n⌉ до n – 1 включительно. Обозначим это число через функцию f(n, k).

Например, для случая стоэтажного дома и k шаров ⌈log₂100⌉ = 7, 100 – 1 = 99, значит 7 ≤ f(100, k) ≤ 99. Вообще говоря, значение f(n, k) довольно быстро падает с увеличением k. Так, f(100, 1) = 99, f(100, 2) = 14,
f(100, 3) = 9, f(100, 4) = 8, f(100, 5) = f(100, 6) = f(100, 7) = … = 7.

Примечательный факт: в случае стоэтажного дома найти x за семь попыток можно, имея всего пять шаров! То есть метод поиска «делением отрезка пополам» не панацея – он быстрый, но не всегда самый оптимальный с точки зрения требуемого числа шаров.

Рекуррентная формула подсчета наименьшего числа испытаний

Итак, как же найти точное значение f(n, k)?
В простейших ситуациях все ясно: f(n, 1) = n – 1 (см. случай А), f(n, k) = ⌈log₂n⌉ при k ≥ log₂n (см. случай Б), в том числе f(1, k) = 0 (если этаж всего один, то он же и является искомым по условию задачи).

Рассмотрим случай n ≥ 2 и k ≥ 2. Предположим, что первым испытанием мы бросили шар с «a»-го этажа, a может быть от 1 до n – 1 включительно (бросать шар с «n»-го этажа бессмысленно). Возможны два исхода:
Исход 1: шар разбился. Это означает, что 1 ≤ x ≤ a. У нас a неисследованных этажей, k – 1 шаров, т.е. чтобы гарантированно найти x нужно ещё f(a, k – 1) испытаний.
Исход 2: шар не разбился. Это означает, что a + 1 ≤ x ≤ n. У нас n – a неисследованных этажей, k шаров, т.е. чтобы гарантированно найти x нужно ещё f(n – a, k) испытаний.
В итоге, после броска шара с «a»-го этажа может понадобиться ещё max{f(a, k – 1), f(n – a, k)} испытаний для гарантированного нахождения x.
Мы хотим минимизировать число испытаний, поэтому берем a таким, чтобы max{f(a, k – 1), f(n – a, k)} было наименьшим, а именно min_a{max{f(a, k – 1), f(n – a, k)}}.

Таким образом, наименьшее число испытаний равно:
f(n, k) = 1 + min_a{max{f(a, k – 1), f(n – a, k)}} (формула 1).

Этой формулы достаточно, для того чтобы вычислить f(n, k) для любых заданных n и k, а также номер этажа a(n, k) = a, с которого нужно бросать шар – он может быть любым из тех, для которых значение max{f(a, k – 1), f(n – a, k)} достигает минимума.
Вычисление легко реализовать, например, в Excel.

Кому интересно

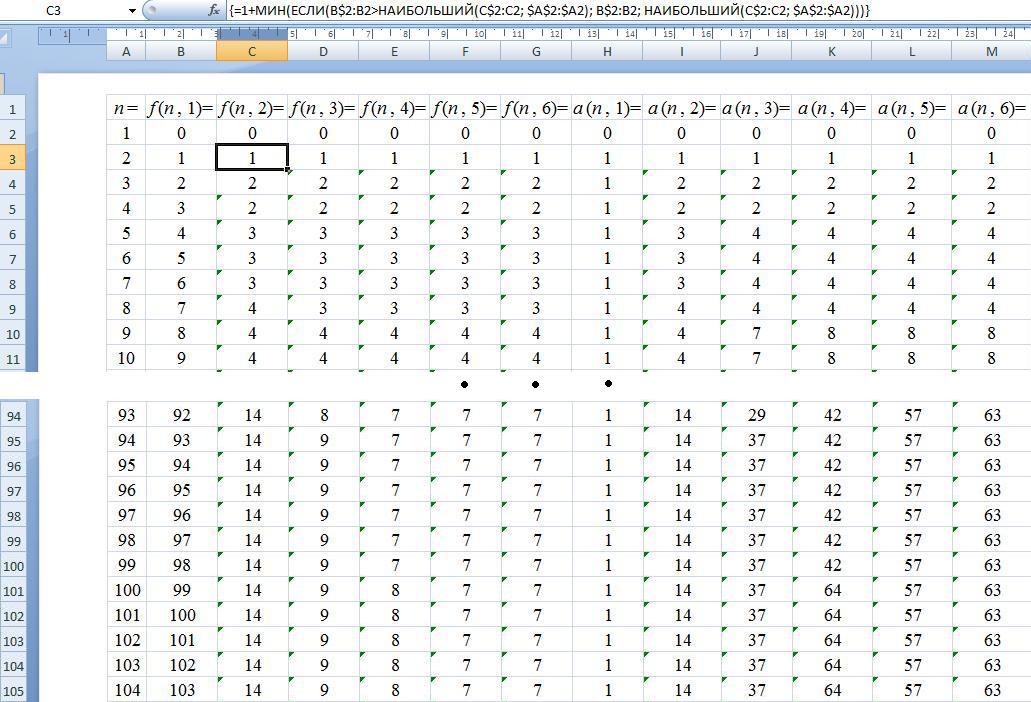
В столбце A, начиная со второй строки, будем записывать значения n по порядку от 1 до требуемого. В столбце B в соответствующих строках будем записывать значения f(n, 1), в столбце C – значения f(n, 2) и так далее, сдвиг на один столбец вправо означает увеличение на один числа шаров.
При n = 1 значение функции f(n, k) равно нулю, поэтому заполняем соответствующую строку нулями.
В ячейку B3 записываем формулу =A3 – 1, так как f(n, 1) = n – 1. Копируем (или растягиваем) её на нужное число строк вниз.
В ячейку C3 записываем формулу:
=1+МИН(ЕСЛИ(B$2:B2>НАИБОЛЬШИЙ(C$2:C2; $A$2:$A2); B$2:B2; НАИБОЛЬШИЙ(C$2:C2; $A$2:$A2)))
и нажимаем CTRL+SHIFT+ENTER, т.е. вводим формулу массива. Копируем (или растягиваем) её на нужное число строк вниз и столбцов вправо.

Значения a(n, k) будем вычислять в столбцах правее тех, которые использованы для вычисления f(n, k), по тому же принципу: строки соответствуют значению n, сдвиг на один столбец вправо означает увеличение на один числа шаров.
В ситуации как на скриншоте, столбец H, начиная с третьей строки, заполняется единицами, так как a(n, 1) = 1 (см. случай А, единственный шар всегда кидаем с первого этажа).
В ячейку I3 записываем формулу:
=МАКС((B$2:B2<C3)*(НАИБОЛЬШИЙ(C$2:C2; $A$2:$A2)<C3)*$A$2:$A2)
и нажимаем CTRL+SHIFT+ENTER, т.е. вводим формулу массива. Копируем (или растягиваем) её на нужное число строк вниз и столбцов вправо.

Алгоритм поиска x

Если мы знаем значения a(n, k), то легко описать алгоритм поиска x за не более чем f(n, k) испытаний.
Вход: n – число этажей дома, k – число шаров.
Выход: x – номер искомого этажа.
Начало алгоритма.
Шаг 1. Инициализируем переменную: x := 1. Переход на шаг 2.
Шаг 2. Условие останова: если n = 1, то вывод x и СТОП, иначе переход на шаг 3.
Шаг 3. Бросим шар с этажа с номером x – 1 + a(n, k). Если шар разбился, то обновляем значения переменных: n := a(n, k), k := k – 1.
Если шар не разбился, то обновляем значения переменных: x := x + a(n, k), n := n – a(n, k). Переход на шаг 2.
Конец алгоритма.

Рассмотрим пример, как найти x за семь испытаний, если у нас сто этажей и пять шаров. Пользуясь значениями a(n, k) из построенной в Excel таблицы, напишем номера этажей, с которых бросаем шар,
в случае если они все время разбиваются:
57 -> 26 -> 11 -> 4 -> 1 (если не разбился, то далее) -> 2 (если не разбился, то далее) -> 3.
Если, например, после броска шара с 26-го этажа он не разбился, оказываемся в ситуации n = 31, k = 4. Тогда последовательность бросков выглядит как:
57 -> 26 -> 26 + 15 = 41 -> 26 + 7 = 33 -> 26 + 3 = 29 -> 26 + 1 = 27 (если не разбился, то далее) -> 27 + 1 = 28.

Все возможные варианты рассматривать не буду. Видно, что алгоритм отличается от метода поиска «делением отрезка пополам».

«Явная» формула подсчета наименьшего числа испытаний

Главный недостаток формулы 1 в том, что на её вычисление нужно довольно много ресурсов. Разрешить эту рекуррентную формулу в явном виде самостоятельно мне удалось только для k = 2 и k = 3 путем поиска и обоснования закономерностей в таблице значений функции. В частности, в первом случае результат такой:
f(n, 2) = ⌈⌉.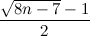

Аналогичные результаты люди получали из других соображений: статья. Правда в ней ответ 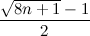, что вызвано немного другим условием задачи – шар не обязан разбиваться при броске с самого верхнего этажа. Если мы хотим учесть такую возможность, то в наш ответ надо подставить вместо n выражение n + 1 (т.е. добавить этаж), и получим формулу из статьи.

Однако постепенно я зашел в тупик, так как общую формулу найти не удавалось, рекуррентное соотношение слишком сложное. Именно в этот момент я обнаружил замечательные идеи пользователей irishoak, Bert, mikhail_vs и других, которые позволяют свести вычисление f(n, k) к решению интересного неравенства.

Для этого нужно рассмотреть еще одну функцию: g(m, k) – наибольшее число этажей, среди которых можно гарантированно найти x за не более чем m испытаний при наличии k шаров.
В простейших ситуациях функция принимает следующие значения: g(m, 1) = m + 1 (см. случай А), g(m, k) = g(m, m) при k > m (так как за m испытаний можно разбить максимум m шаров, то остальные k – m шаров лишние и на значение функции не влияют).
При m ≥ 2, k ≥ 2 можно вывести рекуррентную формулу:
g(m, k) = g(m – 1, k – 1) + g(m – 1, k) (формула 2).

Рекуррентную формулу 2, в отличие от формулы 1, легко разрешить, т.е. выразить g(m, k) в явном виде:
g(m, k) = C_m⁰ + C_m¹ + C_m² + … + C_m^k,
где C_mⁱ – это число сочетаний из m по i, C_mⁱ = m!/(i!(m — i)!).
Это равенство можно вывести «конструктивно», а можно «угадать» и доказать его по индукции, что значительно проще (здесь доказательство не привожу).
Теперь для нахождения наименьшего числа испытаний требуется вычислить:
f(n, k) = ⌈log₂n⌉ при k ≥ log₂n,
f(n, k) = min{натуральное m | C_m⁰ + C_m¹ + C_m² + … + C_m^k ≥ n} при k < log₂n.
Кстати, при выводе рекуррентной формулы для g(m, k) еще одним способом определяется номер этажа, с которого можно бросать шар, чтобы найти x за не более чем f(n, k) испытаний: a(n, k) = g(m – 1, k – 1),
где m = f(n, k), т.е.
a(n, k) = C_{f(n, k) – 1}⁰ + C_{f(n, k) – 1}¹ + C_{f(n, k) – 1}² + … + C_{f(n, k) – 1}^{k – 1} при k < f(n, k) (формула 3),
a(n, k) = 2^{f(n, k) – 1} при k ≥ f(n, k) (формула 4).

Выводы и авантюрная оценка наименьшего числа испытаний

Приступая к задаче, я интуитивно наметил себе план решения – вначале понять принцип поиска нужного этажа (т.е. разработать алгоритм), затем найти, сколько бросков он потребует в худшем случае.
К моему удивлению путь оказался иным – довольно простой алгоритм легко следовал из формул вычисления наименьшего числа испытаний, которое мы обозначили через f(n, k).

Практически ничего не зная о функции f, мы грубо оценили ее как:
log₂n ≤ f(n, k) ≤ n – 1.

Нам известно, что левая граница заведомо достигается при «больших» k, а именно при k ≥ log₂n, а правая – при k = 1. Мы также узнали, что для промежуточных значений k поиск f(n, k) сводится к нахождению наименьшего натурального m (обозначим его m₀), удовлетворяющего неравенству:
C_m⁰ + C_m¹ + C_m² + … + C_m^k ≥ n (неравенство 1).
Однако решить его, чтобы получить по-настоящему явную формулу для f(n, k), представляется нетривиальной задачей. Было бы интересно услышать ваши предложения.

Но даже если неравенство не решается, можно оценить диапазон, в котором находится искомый m₀, он же – значение функции f(n, k).

Вообще говоря, представленную сумму биномиальных коэффициентов можно рассматривать как многочлен степени k от переменной m. Тогда нахождение m₀ из неравенства 1 сводится, по сути, к нахождению положительных корней полинома C_m⁰ + C_m¹ + C_m² + … + C_m^k – n.
Есть методы, которые позволяют оценить корни многочлена, но для этого надо знать его коэффициенты, а в нашем случае они выглядят страшновато (выражаются через жуткие суммы, которые не факт что сворачиваются). Поэтому поступим иначе.

Подберем две функции h₁(m, k) и h₂(m, k) так, чтобы, во-первых, выполнялись неравенства h₁(m, k) ≤ C_m⁰ + C_m¹ + C_m² + … + C_m^k ≤ h₂(m, k), во-вторых, чтобы при фиксированном k легко решались неравенства h₁(m, k) ≥ n и h₂(m, k) ≥ n.
Легко понять, что решение h₂(m, k) ≥ n даст нам оценку искомого m₀ снизу, а решение h₁(m, k) ≥ n – сверху.

Что касается верхней оценки суммы биномиальных коэффициентов (т.е. функции h₂), то лучшее из найденного – неравенство Чернова:
C_m⁰ + C_m¹ + C_m² + … + C_m^k ≤ .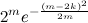
Решение 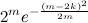≥ n даёт следующую оценку наименьшего числа испытаний снизу:
f(n, k) ≥ 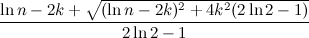при k < .

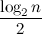Честно, эта формула мне не очень нравится – громоздкая и работает только для «маленьких» k. Но всё же она бывает лучше, чем наша первая – грубая – оценка, хотя и не всегда.
Вообще говоря, нижняя граница диапазона нам не так важна ввиду того, что значение функции довольно быстро падает при увеличении k.

Гораздо интереснее уточнить верхнюю границу. Для этого нужно подобрать h₁. Никаких приемлемых результатов по нижней оценке суммы биномиальных коэффициентов мне найти не удалось. Собственные попытки что-то изобрести привели к забавной ситуации.
Размышляя, я пришел к выводу, что C_mⁱ ≥ 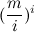при m ≥ i ≥ 1.
В дальнейшем я обнаружил в рассуждениях ошибку, но неравенство по-прежнему кажется мне верным, причем с приличным запасом (что показывают численные эксперименты).
Важнее даже, чтобы выполнялось не само неравенство, а 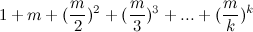≤ C_m⁰ + C_m¹ + C_m² + … + C_m^k, что ещё более вероятно.
К сожалению, формально это пока не доказано, буду благодарен за наводящие мысли или ссылки, а возможно и контрпримеры.

В итоге, я решил продолжить исследование, исходя из предположения, что моя гипотеза верна, поэтому называю полученную оценку авантюрной.
Итак, h₁(m, k) = .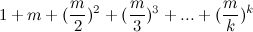

Неравенство h₁(m, k) ≥ n тоже не обязательно решать. Мы знаем коэффициенты при степенях m, поэтому можем оценить корни многочлена h₁ (m, k) – n. Воспользовавшись оценкой Маклорена, получим, что все его положительные корни не превосходят .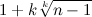

Это означает, что искомое нами m₀ ≤ 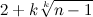(оценка 2).
На мой взгляд, весьма красивая формула – компактная, интересным образом зависит от обеих переменных и, что главное, хорошо сужает диапазон.
Еще один способ оценить f(n, k) сверху – ограничить его значением f(n, 2) = ⌈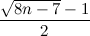⌉. Несмотря на то, что число шаров в этой формуле не учитывается, иногда она всё же дает лучший результат по сравнению с оценкой 2.
Для уверенности можем записать следующую оценку наименьшего числа испытаний сверху:
f(n, k) ≤ min{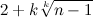, 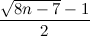+ 1}.

Применив полученные формулы на практике, получим, например, что f(400, 4) лежит в диапазоне от 9 до 19, при реальном значении равном 11. Причем правую границу диапазона даёт именно оценка 2, в то время как f(400, 2) = 28.
Для более экстремальных значений, например, n = 2⁴⁰, k = 10, получим левую границу – 58, правую – 162. Для сравнения: log₂n = 40, f(n, 2) = 1482910, то есть оценки 1 и особенно 2 сработали весьма хорошо. Точное значение можно найти, решая неравенство 1, перебор даёт ответ 76.

Заключение

С учетом всего изложенного можно констатировать, что задача про два стеклянных шара в общем виде, в целом, решена.
Хотя явной формулы для наименьшего числа испытаний не получено, его можно определить, решая перебором или иными методами неравенство 1.
С учетом формул 3 и 4 этого также достаточно для работы несложного алгоритма по поиску нужного этажа.
Аналитические выкладки (оценки 1 и 2) позволяют значительно сузить диапазон, в котором находится наименьшее число испытаний, что может быть полезно в случаях, если вычисление точного значения слишком трудоёмко или не требуется.

P.S.: к моменту опубликования поста мне удалось доказать гипотезу, которую я использовал для оценки 2, а именно:
C_mⁱ ≥ 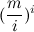при m ≥ i ≥ 1.
Поэтому оценка теперь полноценная, а не авантюрная.

Вместе с тем по-прежнему буду благодарен за ссылки на литературу, где рассматриваются нижние оценки для биномиальных коэффициентов или их суммы.

Автор: LerTush

Источник