Добрый день! Недавно здесь проскакивал пост про уравнение Кеплера и я был слегка поражен тем, что ничего не написано про то, каким образом оно вообще выводится и откуда, как исторически, так и математически. Как известно, Кеплер вывел его из наблюдения движения планет, а Ландау и Лифшиц вывели движение планет из…
Никакая теоретическая механика невозможна без функции Лагранжа. Ее вывод я приводить не буду, скажу лишь, что вся соль в принципе наименьшего действия Гамильтона,
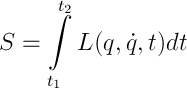
согласно которому, механическая система движется так, что вышеуказанный интеграл, который, кстати, называется действием, имеет наименьшее возможное значение. Возможно, «варьирование функционала» что-то вам говорит — если да, то уравнение Лагранжа (УЛ) (1), оно же уравнение Эйлера, для свободной частицы следует именно оттуда — это один из вариантов его вывода. Если нет, то все чуточку хуже, а именно: мы бы разобрали второй закон Ньютона, потратили около двух страниц на выкладки, ввели понятия обобщенных координат и сил и связей и в конечном итоге пришли бы к тому же варианту. Кстати, именно вторым способом функция Лагранжа (ФЛ) (2) вводится естественным образом, как разница кинетической и потенциальной энергий.
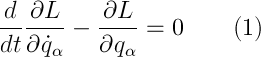
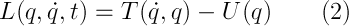
Касательно обозначений, q — обобщенная координата, точка — производная по времени. Важно! Согласно Лагранжева формализма, обобщенные координаты и скорости — независимые величины! В случае свободной частицы (или замкнутой системы, то есть системы, на которую не действуют внешние силы):
Индексы у обобщенных координат обозначают, что вообще это система дифференциальных уравнений для каждой координаты в отдельности.
Если коротко и в обратную сторону, заменив обобщенные координаты на радиус-векторы и скорости:
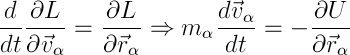
мы получаем уравнение Ньютона из уравнения Лагранжа (помня о том, что производная радиус-вектора по времени равна скорости).
Тут стоит еще добавить, что ФЛ аддитивна, что значит ФЛ системы есть сумма ФЛ ее частей:
Отлично, у нас есть фундамент. Теперь, чтобы дойти до уравнения Кеплера, необходимо построить стены — обобщенные энергию, импульс и момент импульса. Здесь важно сделать маленькое утверждение, которое на самом деле очень большое и имеет название «Теорема Нётер»: наше пространство, по крайней в масштабах тех тел, которые мы описываем:
- однородно,
- изотропно,
- обладает однородным временем.
Таким образом мы можем ввести три закона сохранения, три интеграла движения, то есть величины, сохраняющейся при движении, зависящей исключительно от начальных условий.
Начнем с обобщенной энергии. Самое очевидное, что я могу сделать — вывести ее. Воспользуемся однородностью времени, а именно: ФЛ не зависит явно от времени, возьмем полную производную ФЛ и преобразуем, подставляя УЛ:
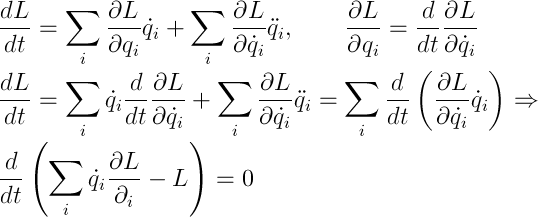
Откуда следует
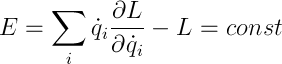
Готово. Кстати, механические системы с сохраняющейся энергией называются консервативными.
Сохранение обобщенного импульса следует из однородности пространства, а конкретно из свободы параллельного переноса системы в пространстве. Рассмотрим бесконечно малый перенос системы в пространстве на эпсилон, т.е. радиус-векторы частей системы изменятся как (1). Изменение ФЛ запишется как (2), что в силу произвольности эпсилон можно переписать так в виде равной нулю суммы частных производных. Дальше просто, (3) и мы видим, что суммарный импульс (4) не изменяется при движении.
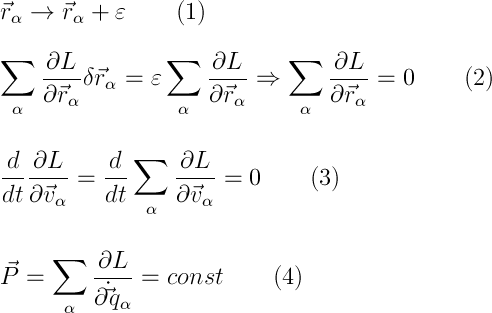
Здесь же введем понятие центра инерции. Вообще механическая система интуитивно представима в виде некоторой точки, движущейся по прямой и остальных тел, которые каким-то образом движутся уже относительно этой точки. Так вот эта точка и есть центр инерции, то есть мы замкнутую механическую систему представим в виде некоторой точки с суммарной массой, а все остальное засунем во внутреннюю энергию системы.
С моментом импульса, он же момент количества движения, все получается подобным образом, поэтому я просто выпишу результат:
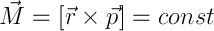
Подытожим: у нас есть УЛ, ФЛ и три интеграла движения: энергия, импульс и момент количества движения.
Можем переходить наконец к тому, из-за чего я отнимаю ваше время :) То, из чего следует в частном случае уравнение Кеплера, называется «задача двух тел». Для начала упростим ее. Напишем ФЛ двух тел (1) и введем вектор их взаимного расстояния (2). Заодно поместим начало координат в центре инерции, что даст (3). Из второго и третьего уравнений найдем радиус-векторы обоих точек (4) и подставим в первое (5). Здесь введена приведенная масса (6).
Таким образом задача двух тел сведена к задаче одного тела в некотором центральном поле.
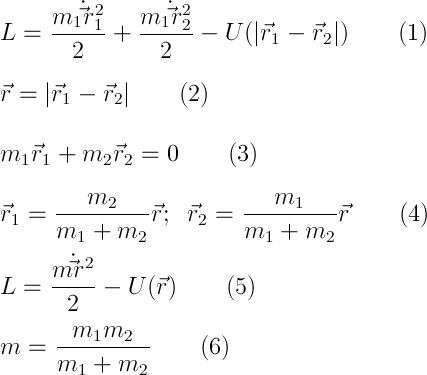
Рассмотрим момент импульса в центральном поле M=[rp]. Отсюда М и r перпендикулярны, а из постоянства М (интеграл движения, помните?) видно, что радиус-вектор системы лежит всегда в одной плоскости — у нас плоское движение, а значит самое время ввести цилиндрическую систему координат с центром в силовом центре (простите за тавтологию) и осью z, перпендикулярной плоскости движения — по сути полярную. Перепишем ФЛ:
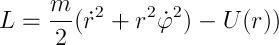
и посмотрим на координату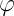 
— ее нет! Есть только ее производная по времени, что дает нам право обозвать ее циклической и сказать, что соответствующий ей обобщенный импульс сохраняется, а решение задачи упрощается. В данном случае он совпадает с моментом количества движения
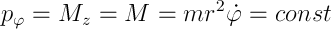
Также в ФЛ не входит явно время, значит сохраняется заодно и энергия системы. Проведя серию выкладок
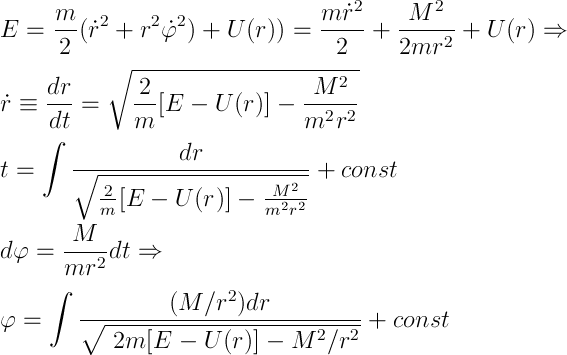
получим решение задачи в квадратурах, то есть в интегралах. Заодно введем эффективную потенциальную энергию
А при чем тут уравнение Кеплера, слышно вопрос с задних рядов. Хорошо-хорошо, уговорили, я и сам как раз собирался…
Давайте рассмотрим задачу о движении в центральном потенциальном поле
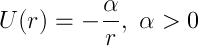
Знак минус обозначает притяжение (а знак плюс означал бы отталкивание, что в данном случае нам не интересно — частица отразится и уйдет на бесконечность). Эта задача даже имеет собственное имя — да, задача Кеплера. Построим эффективную потенциальную энергию и ее график. Очевидно, что при стремлении r к нулю, она стремится к бесконечности, а при стремлении радиус-вектора к бесконечности, соответственно, к нулю.
Из графика очевидно, что при энергии Е > 0 движение будет инфинитным, то есть частица уйдет на бесконечность, а при E < 0 — финитным. Форма траектории будет определяться общей формулой
которая после подстановки в нее вида потенциала, введения пары обозначений
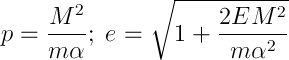
преобразования и выбора начала отсчета угла так, что const=0, станет
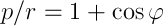
где р и е — параметр и эксцентриситет орбиты соответственно. Вот оно, уравнение Кеплера.
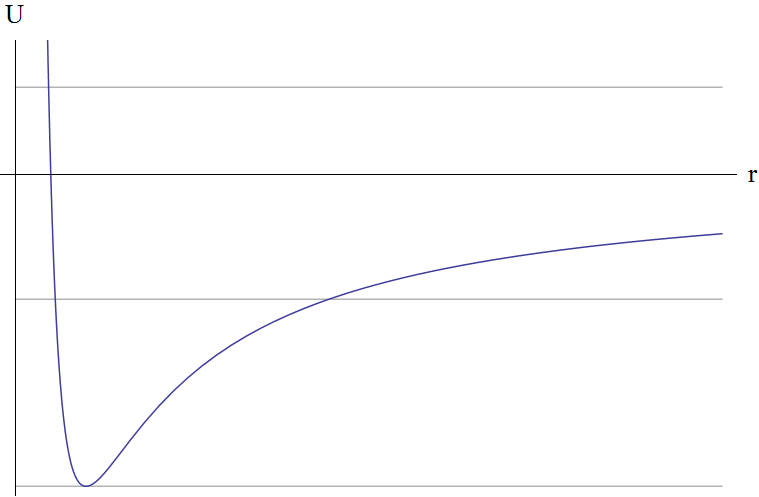
Проанализируем полученные результаты. Для этого еще раз посмотрим на график эффективной потенциальной энергии.
Серые линии — возможные значения энергии системы. То есть, они, конечно, возможны все, кроме меньших 
, но рассмотрим мы эти. Снизу вверх:
- самая нижняя точка — точка минимума. E<0, e=0 — траектория движения — окружность. Случай редкий и очень простой.
- чуть выше. Е<0, 0<e<1 — эллипс.
Движение финитно, также можно определить большую и малую полуоси эллипса как
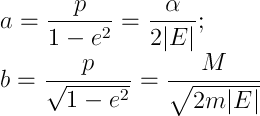
что следует непосредственно из формул аналитической геометрии (здесь я, пожалуй, отправлю вас к Выгодскому или ближе, к Вики). Наименьшее и наибольшее расстояния до фокуса эллипса, перигелий и афелий, соответственно
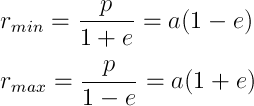
что можно было, вообще говоря, получить в лоб из
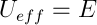. Время обращения по орбите получим из второго закона Кеплера 
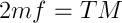. Для эллипса секторная скорость 
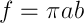, а значит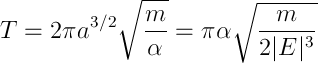 
Так мы получили третий закон Кеплера
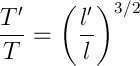. Здесь следует отметить, что период зависит только от энергии частицы.
- Е=0, е=1. Траектория инфинитна, это парабола с
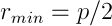. Такая траектория будет у частицы, движущейся с бесконечности из состояния покоя.
- E>0, e>1. Траектория опять инфинитна, но на этот раз это гипербола, с перигелием
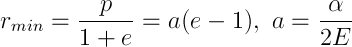
Пожалуй, это все, что я хотел бы рассказать про одну из фундаментальных задач механики. Задача Кеплера часто используется для проверки систем математического моделирования, как очень хорошо изученная и вместе с тем простая. Вместе с задачей о гармоническом осцилляторе это одна из двух задач о движении тела по замкнутой траектории, когда тело возвращается в исходную точку с той же самой скоростью. Задача Кеплера используется для построения новых методов классической механики, в частности Гамильтонова формализма, уравнения Гамильтона-Якоби и системы переменных «действие-угол».
Автор: xtotdam
