Введение
Добрый день, уважаемые читатели.
В прошлых статьях, на практических примерах, мной были показаны способы решения задач классификации (задача кредитного скоринга) и основ анализа текстовой информации (задача о паспортах). Сегодня же мне бы хотелось коснуться другого класса задач, а именно восстановления регрессии. Задачи данного класса, как правило, используются при прогнозировании.
Для примера решения задачи прогнозирования, я взял набор данных Energy efficiency из крупнейшего репозитория UCI. В качестве инструментов по традиции будем использовать Python c аналитическими пакетами pandas и scikit-learn.
Описание набора данных и постановка задачи
Дан набор данных, котором описаны следующие атрибуты помещения:
| Поле | Описание | Тип |
|---|---|---|
| X1 | Относительная компактность | FLOAT |
| X2 | Площадь | FLOAT |
| X3 | Площадь стены | FLOAT |
| X4 | Площадь потолка | FLOAT |
| X5 | Общая высота | FLOAT |
| X6 | Ориентация | INT |
| X7 | Площадь остекления | FLOAT |
| X8 | Распределенная площадь остекления | INT |
| y1 | Нагрузка при обогреве | FLOAT |
| y2 | Нагрузка при охлаждении | FLOAT |
В нем 

Предварительный анализ данных
Для начала загрузим наши данные и посмотрим на них:
from pandas import read_csv, DataFrame
from sklearn.neighbors import KNeighborsRegressor
from sklearn.linear_model import LinearRegression, LogisticRegression
from sklearn.svm import SVR
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.cross_validation import train_test_split
dataset = read_csv('EnergyEfficiency/ENB2012_data.csv',';')
dataset.head()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | Y1 | Y2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 2 | 0 | 0 | 15.55 | 21.33 |
| 1 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 3 | 0 | 0 | 15.55 | 21.33 |
| 2 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 4 | 0 | 0 | 15.55 | 21.33 |
| 3 | 0.98 | 514.5 | 294.0 | 110.25 | 7 | 5 | 0 | 0 | 15.55 | 21.33 |
| 4 | 0.90 | 563.5 | 318.5 | 122.50 | 7 | 2 | 0 | 0 | 20.84 | 28.28 |
Теперь давайте посмотрим не связаны ли между собой какие-либо атрибуты. Сделать это можно рассчитав коэффициенты корреляции для всех столбцов. Как это сделать было описано в предыдущей статье:
dataset.corr()
| X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | Y1 | Y2 | |
|---|---|---|---|---|---|---|---|---|---|---|
| X1 | 1.000000e+00 | -9.919015e-01 | -2.037817e-01 | -8.688234e-01 | 8.277473e-01 | 0.000000 | 1.283986e-17 | 1.764620e-17 | 0.622272 | 0.634339 |
| X2 | -9.919015e-01 | 1.000000e+00 | 1.955016e-01 | 8.807195e-01 | -8.581477e-01 | 0.000000 | 1.318356e-16 | -3.558613e-16 | -0.658120 | -0.672999 |
| X3 | -2.037817e-01 | 1.955016e-01 | 1.000000e+00 | -2.923165e-01 | 2.809757e-01 | 0.000000 | -7.969726e-19 | 0.000000e+00 | 0.455671 | 0.427117 |
| X4 | -8.688234e-01 | 8.807195e-01 | -2.923165e-01 | 1.000000e+00 | -9.725122e-01 | 0.000000 | -1.381805e-16 | -1.079129e-16 | -0.861828 | -0.862547 |
| X5 | 8.277473e-01 | -8.581477e-01 | 2.809757e-01 | -9.725122e-01 | 1.000000e+00 | 0.000000 | 1.861418e-18 | 0.000000e+00 | 0.889431 | 0.895785 |
| X6 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 0.000000e+00 | 1.000000 | 0.000000e+00 | 0.000000e+00 | -0.002587 | 0.014290 |
| X7 | 1.283986e-17 | 1.318356e-16 | -7.969726e-19 | -1.381805e-16 | 1.861418e-18 | 0.000000 | 1.000000e+00 | 2.129642e-01 | 0.269841 | 0.207505 |
| X8 | 1.764620e-17 | -3.558613e-16 | 0.000000e+00 | -1.079129e-16 | 0.000000e+00 | 0.000000 | 2.129642e-01 | 1.000000e+00 | 0.087368 | 0.050525 |
| Y1 | 6.222722e-01 | -6.581202e-01 | 4.556712e-01 | -8.618283e-01 | 8.894307e-01 | -0.002587 | 2.698410e-01 | 8.736759e-02 | 1.000000 | 0.975862 |
| Y2 | 6.343391e-01 | -6.729989e-01 | 4.271170e-01 | -8.625466e-01 | 8.957852e-01 | 0.014290 | 2.075050e-01 | 5.052512e-02 | 0.975862 | 1.000000 |
Как можно заметить из нашей матрицы, коррелируют между собой следующие столбы (Значение коэффициента корреляции больше 95%):
- y1 --> y2
- x1 --> x2
- x4 --> x5
Теперь давайте выберем, какие столбцы их наших пар мы можем убрать из нашей выборки. Для этого, в каждой паре, выберем столбцы, которые в большей степени оказывают влияние на прогнозные значения Y1 и Y2 и оставим их, а остальные удалим.
Как можно заметить и матрицы с коэффициентами корреляции на y1,y2 больше значения оказывают X2 и X5, нежели X1 и X4, таким образом мы можем последние столбцы мы можем удалить.
dataset = dataset.drop(['X1','X4'], axis=1)
dataset.head()
Помимо этого, можно заметить, что поля Y1 и Y2 очень тесно коррелируют между собой. Но, т. к. нам надо спрогнозировать оба значения мы их оставляем «как есть».
Выбор модели
Отделим от нашей выборки прогнозные значения:
trg = dataset[['Y1','Y2']]
trn = dataset.drop(['Y1','Y2'], axis=1)
После обработки данных можно перейти к построению модели. Для построения модели будем использовать следующие методы:
- Метод наименьших квадратов
- Случайный лес
- Логистическую регрессию
- Метод опорных векторов
- Метод ближайших соседей
Теорию о данным методам можно почитать в курсе лекций К.В.Воронцова по машинному обучению.
Оценку будем производить с помощью коэффициента детерминации (R-квадрат). Данный коэффициент определяется следующим образом:
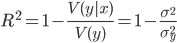
, где 
Коэффициент принимает значение на промежутке 
Ну что же теперь можно перейти непосредственно к построению модели и выбору модели. Давайте поместим все наши модели в один список для удобства дальнейшего анализа:
models = [LinearRegression(), # метод наименьших квадратов
RandomForestRegressor(n_estimators=100, max_features ='sqrt'), # случайный лес
KNeighborsRegressor(n_neighbors=6), # метод ближайших соседей
SVR(kernel='linear'), # метод опорных векторов с линейным ядром
LogisticRegression() # логистическая регрессия
]
Итак модели готовы, теперь мы разобьем наши исходные данные на 2 подвыборки: тестовую и обучающую. Кто читал мои предыдущие статьи знает, что сделать это можно с помощью функции train_test_split() из пакета scikit-learn:
Xtrn, Xtest, Ytrn, Ytest = train_test_split(trn, trg, test_size=0.4)
Теперь, т. к. нам надо спрогнозировать 2 параметра 
#создаем временные структуры
TestModels = DataFrame()
tmp = {}
#для каждой модели из списка
for model in models:
#получаем имя модели
m = str(model)
tmp['Model'] = m[:m.index('(')]
#для каждого столбцам результирующего набора
for i in xrange(Ytrn.shape[1]):
#обучаем модель
model.fit(Xtrn, Ytrn[:,i])
#вычисляем коэффициент детерминации
tmp['R2_Y%s'%str(i+1)] = r2_score(Ytest[:,0], model.predict(Xtest))
#записываем данные и итоговый DataFrame
TestModels = TestModels.append([tmp])
#делаем индекс по названию модели
TestModels.set_index('Model', inplace=True)
Как можно заметить из кода выше, для роасчета коэффициента  используется функция r2_score().
используется функция r2_score().
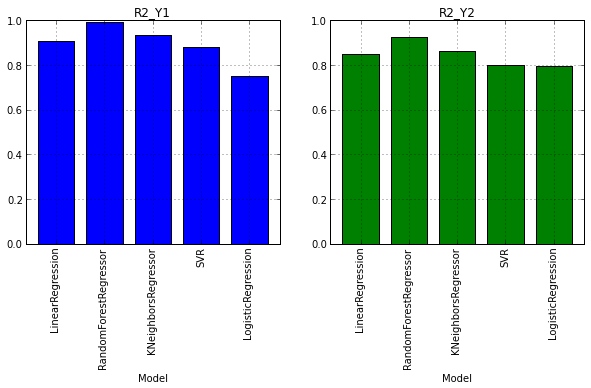
Итак, данные для анализа получены. Давайте теперь построим графики и посмотрим какая модель показала лучший результат:
fig, axes = plt.subplots(ncols=2, figsize=(10,4))
TestModels.R2_Y1.plot(ax=axes[0], kind='bar', title='R2_Y1')
TestModels.R2_Y2.plot(ax=axes[1], kind='bar', color='green', title='R2_Y2')
Анализ результатов и выводы
Из графиков, приведенных выше, можно сделать вывод, что лучше других с задачей справился метод RandomForest (случайный лес). Его коэффициенты детерминации выше остальных по обоим переменным:
ля дальнейшего анализа давайте заново обучим нашу модель:
model = models[1]
model.fit(Xtrn, Ytrn)
При внимательном рассмотрении, может возникнуть вопрос, почему в предыдущий раз и делили зависимую выборку Ytrn на переменные(по столбцам), а теперь мы этого не делаем.
При внимательном рассмотрении, может возникнуть вопрос, почему в предыдущий раз и делили зависимую выборку Ytrn на переменные(по столбцам), а теперь мы этого не делаем.
Дело в том, что некоторые методы, такие как RandomForestRegressor, может работать с несколькими прогнозируемыми переменными, а другие (например SVR) могут работать только с одной переменной. Поэтому на при предыдущем обучении мы использовали разбиение по столбцам, чтобы избежать ошибки в процессе построения некоторых моделей.
Выбрать модель это, конечно же, хорошо, но еще неплохо бы обладать информацией, как каждый фактор влиет на прогнозное значение. Для этого у модели есть свойство feature_importances_.
С помощью него, можно посмотреть вес каждого фактора в итоговой моделей:
model.feature_importances_
array([ 0.40717901, 0.11394948, 0.34984766, 0.00751686, 0.09158358,
0.02992342])
В нашем случае видно, что больше всего на нагрузку при обогреве и охлаждении влияют общая высота и площадь. Их общий вклад в прогнозной модели около 72%.
Также необходимо отметить, что по вышеуказанной схеме можно посмотреть влияние каждого фактора отдельно на обогрев и отдельно на охлаждение, но т. к. эти факторы у нас очень тесно коррелируют между собой (
Заключение
В статье я постарался показать основные этапы при регрессионном анализе данных с помощью Python и аналитческих пакетов pandas и scikit-learn.
Необходимо отметить, что набор данных специально выбирался таким образом чтобы быть максимально формализованым и первичная обработка входных данных была бы минимальна. На мой взгляд статья будет полезна тем, кто только начинает свой путь в анализе данных, а также тем кто имеет хорошую теоретическую базу, но выбирает инструментарий для работы.
Файл консоли IPython Notebook: EnergyEfficiency.ipynb
Автор: kuznetsovin







![Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс] Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2024%2F05%2F10%2Fkak-obhitrit-mozg-i-zastavit-ego-polyubit-slojnye-zadachi-dofaminovyi-detoks-9.jpg&w=100&h=100&zc=1&q=75)