Привет всем. Недавно на Хабре появилась статья, расписывающая взлом crackme от лаборатории Касперского с конференции ZeroNights 2013. У меня тоже получилось взломать этот crackme, но я использовал несколько иной подход для создания ключей, чем Дарвин, потому что заметил, что в crackme используются матричные операции. В отличие от Дарвина я использовал только дебаггинг при помощи OllyDbg.
Вводим случайные значения. Получаем MessageBox с Fail:
Открывем окно Modules( большая M) в олли. Нажимаем Ctrl + B (Search). Вводим в поле ASCII значение fail. Хит на поиск — нашли:
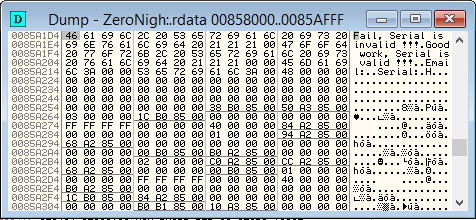
Правой кнопкой мыши на первый байт сообщения, Breakpoit -> Memory -> On Access.
Запускаем отладку. Вводим те же значения в поля crackme. Попадаем на передачу параметров MessageBox:
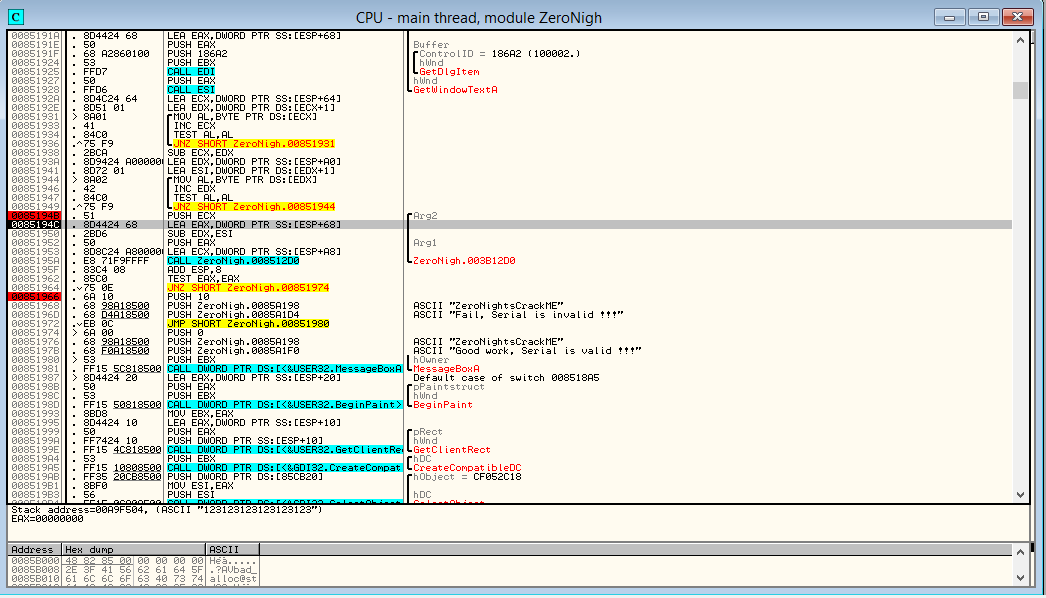
Перед push с нашей строчкой виден условный переход JNZ. Перед ним TEST EAX,EAX. То есть, если EAX не равен нулю, то вылетает MessageBox со строкой
Good work, serial is valid!
. Смотрим, откуда получаем EAX. Перед сравнением есть CALL. Видимо, в этой функции и происходит проверка ключа. Посмотрим, что ей передается. Через стэк происходит передача длины пароля и указатель на строку с почтой. В регистре ECX передается указатель на строку с паролем. Входим в функцию:
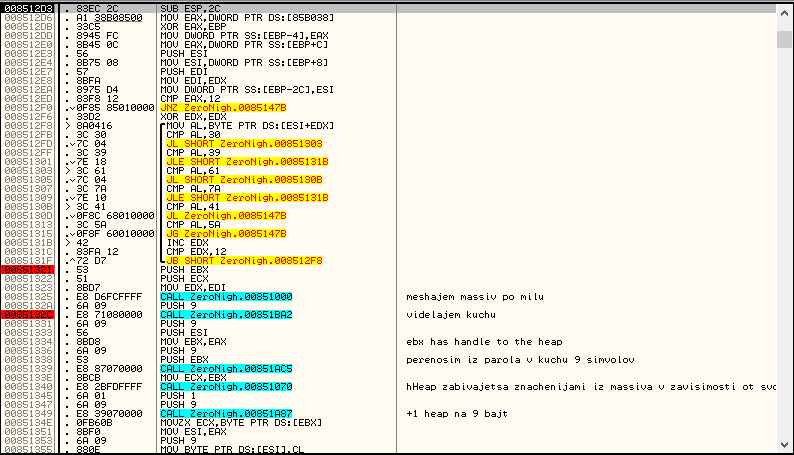
Смотрим на первый JNZ. Перед ним длина пароля сравнивается с 0x12 (18 в десятеричной). Если не соответствует — Fail. Дальше идет цикл (он выделен черной скобой слева), в котором идет проверка символов пароля. Они должны принадлежать множествам 0-9 и a-z, причем заглавные буквы не принимаются. По комментариям справа можно понять, что не все функции важны для реверса. Некоторые — это просто функции копирования или выделения массивов и не представляют особого интереса. Первая функция после цикла очень важна, поэтому подробно ее рассмотрим:
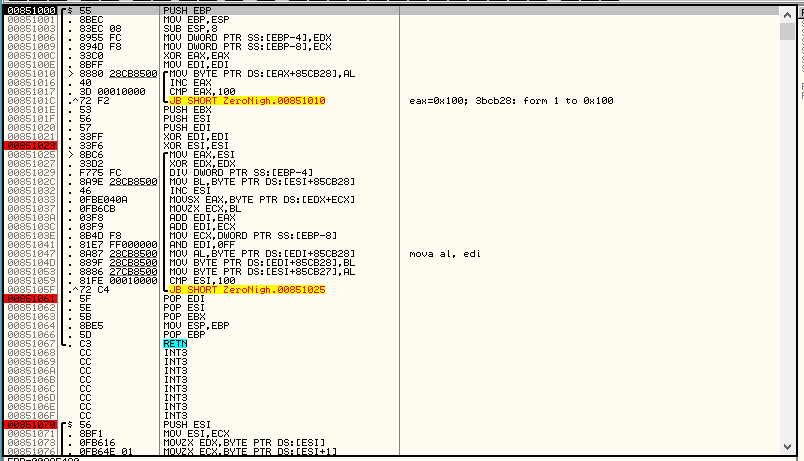
Сразу заметны два цикла. Что же в них происходит? В первом мы заполняем массив в памяти значениями от 0 до 255.
Во втором цикле все не так просто. Взяты два указателя: на массив, заполненный в первом цикле, и на строку с почтой. Берется элемент массива по номеру цикла и символ из почты по номеру цикла по модулю длины почты. Эти байты суммируются по модулю 256 (операция AND EDI, 0xFF эквивалентна __edi % 0x100 в синтаксисе С). Получаются 2 номера элемента по шагу цикла и полученный за счет почты. Эти 2 элемента меняются местами. Почта — это ключ, при помощи которого осуществляется подстановка элементов от 0 до 256. Попросту перемешали массив. Выходим из этой функции назад в общую. Далее происходит выделение массива на 9 байт и копирование в него первых 9-ти символов пароля. Не будем рассматривать эти функции. Зайдем в функцию с комментарием на транслите, начинающимся с «hHeap zabivajetsa»:
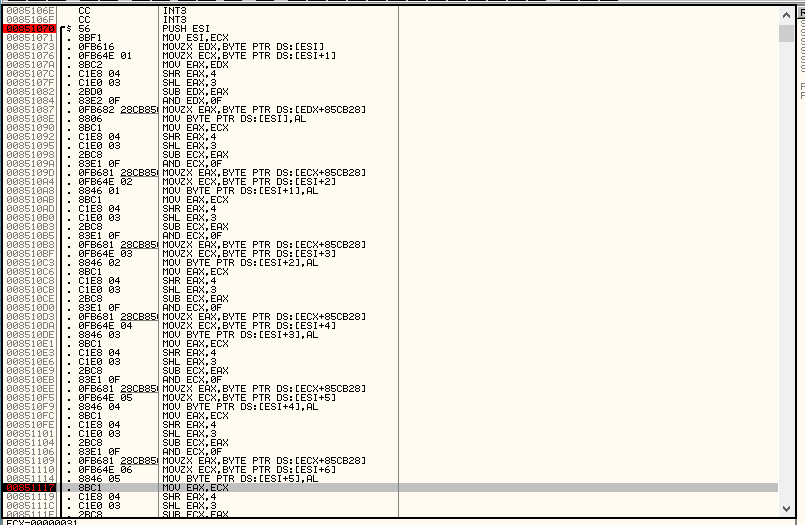
Выглядит страшно, но если присмотреться, можно увидеть, что действия повторяются, а значит перед нами развернутый цикл. Достаточно рассмотреть лишь одну итерацию, все остальное происходит идентично.
В EDX помещается первый символ массива из 9-ти байт. То есть первый символ пароля. Дальше магия:
MOV EAX,EDX
SHR EAX,4
SHL EAX,3
SUB EDX,EAX
AND EDX, 0F
На C это будет:
EDX=(EDX- ((EDX >>4 )<<3))%16
Заменяем символ пароля в hHeap на значение из нашего замешанного массива по номеру EDX. Для остальных символов аналогично. Выходим из функции.
Выделяется еще один массив на 9 байт и в него переносятся значения из первого массива, но по определенным правилам:
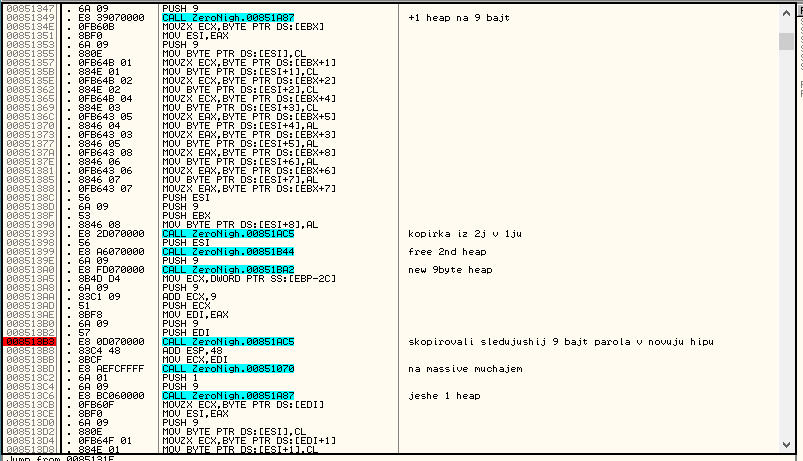
Перемещение -это блок из MOV и MOVZX. Пусть первый массив A, а второй — B. На С:
b[0]=a[0];
b[1]=a[1];
b[2]=a[2];
b[3]=a[5];
b[4]=a[3];
b[5]=a[4];
b[6]=a[8];
b[7]=a[6];
b[8]=a[7];
После этого копируем из второго в первый. Получается, просто перемешали.
Все действия с массивом из девяти байт повторяются для второй части пароля. Получаем два массива:
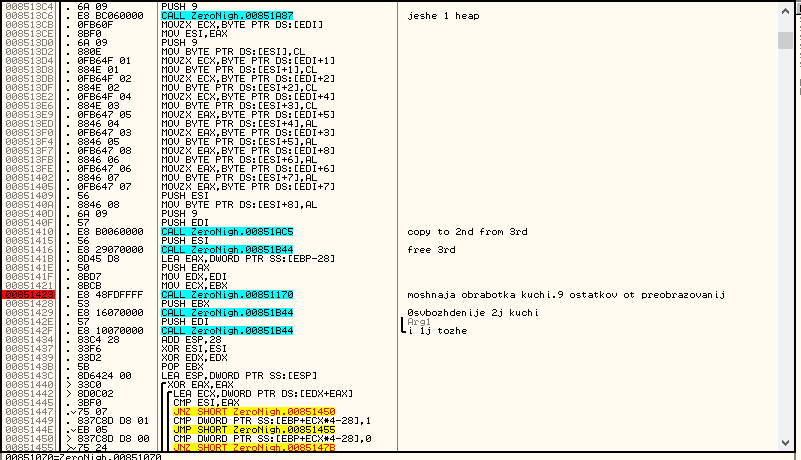
Заходим в функцию «moshnaja obrabotka kuchi»:

Видим перенос второго массива в стэк. Массив обозначим B, а начало области, в которую переносим — D. На С:
D[0]=B[0];
D[1]=B[3];
D[2]=B[6];
D[3]=B[1];
D[4]=B[4];
D[5]=B[7];
D[6]=B[2];
D[7]=B[5];
D[8]=B[8];
Дальше длинный цикл, который проходит 3 раза:
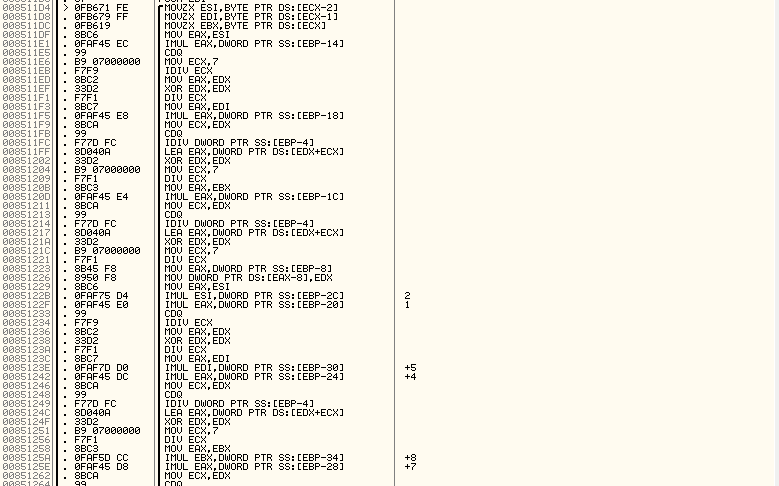
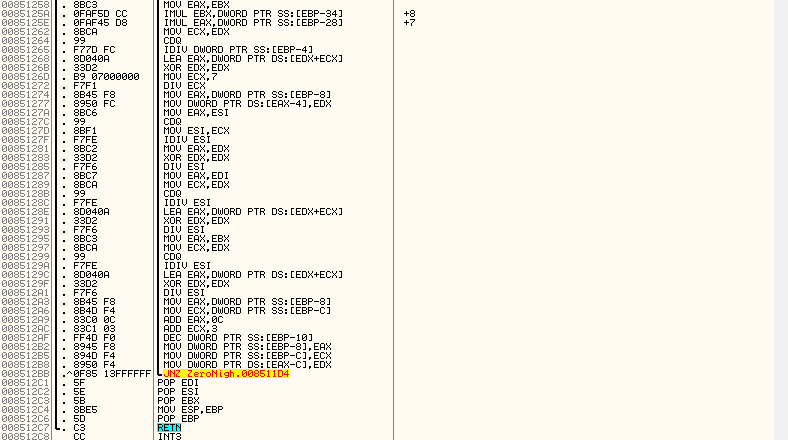
Не у всех хватит терпения, поэтому просто заменим его на алгоритм на С. Пусть A — первый массив, D — массив в стэке, а E — новый массив на вывод все остальное — промежуточные переменные, а я — декомпилятор. Тогда:
for(int i=0;i<3;i++){
X[0]=A[0+i*3];
X[1]=A[1+i*3];
X[2]=A[2+i*3];
E[0+i*3]=((X[0]*D[0])%7+(X[1]*D[1])%7+(X[2]*D[2])%7)%7;
E[1+i*3]=((X[0]*D[3])%7+(X[1]*D[4])%7+(X[2]*D[5])%7)%7;
E[2+i*3]=((X[0]*D[6])%7+(X[1]*D[7])%7+(X[2]*D[8])%7)%7;
}
Выходим из функции, и массив значений в E сравнивается с массивом [1,0,0,0,1,0,0,0,1]:
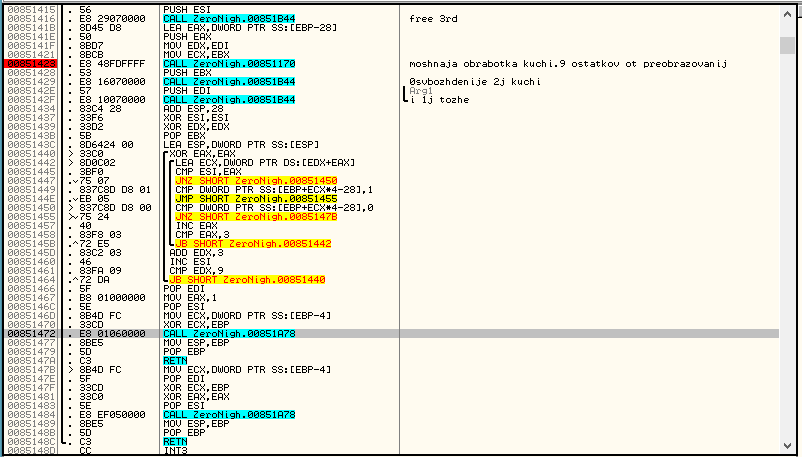
Если совпал, то серийник правильный.
Так пр чем же здесь матрицы. Во-первых, любой массив из девяти элементов можно представить как матрицу 3 на 3. Воспользуемся этим предположением. Получается, что две части пароля — это две матрицы. Помните ту странную перетасовку:
b[0]=a[0];
b[1]=a[1];
b[2]=a[2];
b[3]=a[5];
b[4]=a[3];
b[5]=a[4];
b[6]=a[8];
b[7]=a[6];
b[8]=a[7];
Каждая строчка матрицы сдвигается на свой номер.
Теперь внимательнее посмотрим на перенос второго массива в стэк:
D[0]=B[0];
D[1]=B[3];
D[2]=B[6];
D[3]=B[1];
D[4]=B[4];
D[5]=B[7];
D[6]=B[2];
D[7]=B[5];
D[8]=B[8];
А это интерполяция матрицы. Зачем нужна интерполяция? Да потому что функция, принимающая на вход два массива по девять байт, перемножает их как матрицы. А при чем здесь % 7? Все просто. В ячейках матрицы используется модульная арифметика в поле по модулю 7.
Тогда понятен и массив [1,0,0,0,1,0,0,0,1]. В матричном представлении — это единичная матрица.
Итак, как же нам найти ключ под свою почту? Кейген я не писал, потому что не под любую почту существует ключ, и сейчас вы поймете почему.
После перемешивания массива почтой мы получаем 16 элементов, которые можем использовать. То есть мы можем поставить любой из этих элементов в любую ячейку двух наших матриц. Поскольку дальше будет использоваться только модульная арифметика, то можно установить эквивалентность этих элементов членам поля по модулю 7. Из этих элементов нам нужно подобрать две противоположные матрицы, чтобы при перемножении получилась единичная матрица. Пробуем:
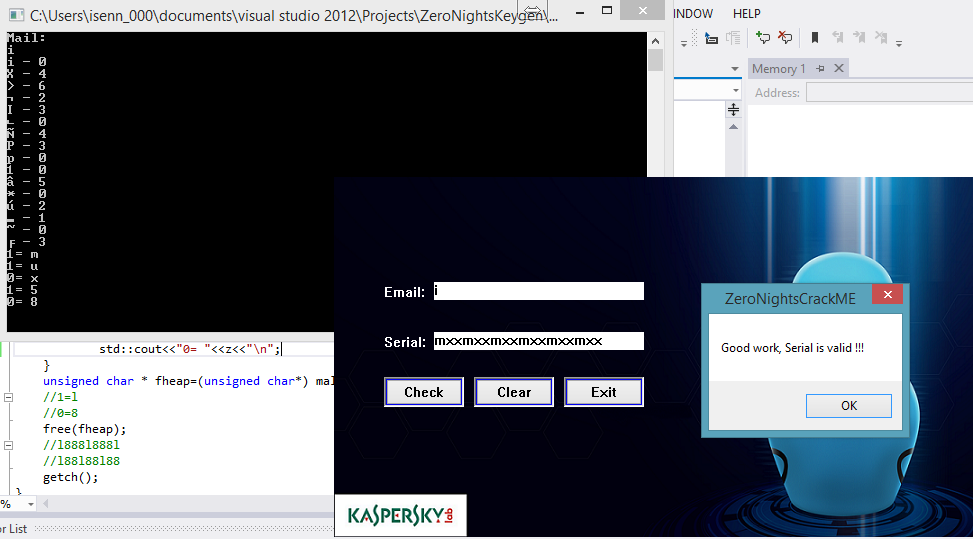
Главное — не забыть про смещение на номер строки.
Как мы подбираем противоположные матрицы:
Находим символ, превращающийся в 0 и находим два символа, превращающиеся в противоположные элементы (например 4 и 2).
Если у нас есть 1 — нам повезло.
Проблема Кейгена в том, что не всегда у нас есть элемент, который переходит в ноль. В таком случае найти две противоположные матрицы невозможно.
Любые советы и комментарии приветствуются. Спасибо, что дочитали до конца.
Автор: Rumata888






