Это достаточно вольный перевод статьи. Дело в том, что несмотря на конструкции в одну строчку, материал сложен для понимания.
Беря во внимание то, что в комментариях Прелюдия или как полюбить Haskell просили, чтобы код был понятный, я внёс достаточно ремарок, и, надеюсь, код будет понятен и тем, кто далёк от Хаскеля.
Давайте начнём с самого трудного — с самого заголовка: многим непонятны все его слова.
Хаскель — это чистый и ленивый функциональный язык.
Лёб — это немецкий математик, о котором мы поговорим чуть позже.
Ну, и наконец, самое интересное — странные петли.
Странные петли — это запутанные категории, когда двигаясь вверх или вниз в иерархической системе, находишь то же самое, откуда начал движение.
Зачастую такие петли содержат само-референтные ссылки.
Например, подобной странной петлёй обладает рекурсивные акронимы: «PHP — PHP: Hypertext Preprocessor».
Ну, и на сегодняшний день наиболее загадочным словом, содержащим странные петли, является понятие «я».
Странные петли будоражат людей своей красотой. И очень приятно, когда находишь их в самых неожиданных местах. Очень интересные функции со странными петлями можно написать на Хаскеле.
Немецкий математик Лёб мигрировал в 39-м году ХХ-го столетия в Великобританию. Лёб, в частности, развивал математическую логику и миру прежде всего известен Теоремой Лёба. Это теорема развивала труды Гёделя о неполноте математики. Теорема Лёба о взаимосвязи между доказуемостью утверждения и самим утверждением, она гласит, что
во всякой теории, включающей аксиоматику Пеано (аксиоматика о натуральных числах), для любого высказывания P доказуемость высказывания «если доказуемо P, тогда P истинно» возможна только в случае доказуемости самого высказывания P.
Всю эту сложность высказывания можно записать символически:
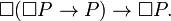
Можно ли такую функцию написать на Хаскеле?! Можно! И всего в одну строчку!
Loeb
loeb — одна из тех функций на Хаскеле, которая выглядит обворожительно, сумасшедшая, простая и сложная одновременно.
- Функцию очень лего написать
- Функцию сложно понять
- Функцию легко использовать
- Функция объяснима
Реализация
Чувствуете себя умными? Давайте изменим это, представляю вам функцию loeb:
loeb :: Functor f => f (f a -> a) -> f a
loeb x = go where go = fmap ($ go) x
Чувствуете всю красоту?! Тогда переходите к следующему разделу.
Нет? Хм… может вы просто не знаете хорошо Хаскеля? Тогда я объясню подробнее.
Некоторые догадливые спросят, почему тут две строчки, а не одна, и будут правы. Но лишь частично. Дело в том, что первая строчка — это подпись: объявление, с какими типами, со сколькими параметрами работает функция. Однако, это сточка является необязательной — если её не писать, интерпретатор (и компилятор) сами выведут типы:
loeb :: Functor f => f (f a -> a) -> f a
Подпись делится на три части — вначале пишем имя функции, далее говорим, что мы хотим объявить тип, ставим ::, далее до жирной стрелочки (=>) мы пишем ограничения на параметры — объясню чуть ниже, пока это не важно. Ну и напоследок — собственно, типы:
f (f a -> a) -> f a, посмотрите, насколько запись близка к теореме Лёба: 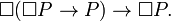 — да один в один!
— да один в один!
Замечу, функция записана без использования библиотечных функций!
Прежде чем объяснить, что подпись означает, пока пройдёмся по самой функции, давайте не мелочиться, и запишем функцию в 3 строчки, как это сделает любой порядочный хаскелист:
loeb :: Functor f => f (f a -> a) -> f a
loeb x = go
where
go = fmap ($ go) x
Тут видно, что слово where — служебное и даёт определить внутреннюю функцию.
Как читать?… Ах да, надо сказать, что в Хаскеле нет лишних скобок, и там где в большинстве языков запишут
f (x, y, z) = ..., в Хаскеле напишут всего лишь f x y z = ...
Из кода видно, что функция loeb — функция от одного аргумента х и определяется она через функцию go.
Функция go определяется через Функтор и функцию fmap. Сама же функция fmap является обобщением функции map для списков и определяется следующим образом:
class Functor f where
fmap :: (a -> b) -> f a -> f b
Тут всего лишь декларация. Классы ООП никак не связаны с классами типов. В нашем случае особо понимать не надо первую строчку, там просто говорится, что f будет полиморфным в функции fmap.
Итак посмотрим внимательно на подпись, чтобы понять, что она означает.
Сказано, что функция fmap — функция от двух аргументов — (a -> b) и f a, на выходе получается тип f b.
Легко понять, что (a -> b) — это функция от одного аргумента, берущая на вход какое-либо значение (обобщённо назовём этот тип a, он может быть любым — например строкой, числом или файлом) и на выходе получается тоже какой-либо тип (обозначим его b, помня, что b в частности может быть и a).
f a — можно понимать как некое сложное значение, зависящее от a и проще будет понять, если читать как f(a)
Если вы откроете определения функтора в математике, увидите удивительную схожесть.
То есть, если отвлечься от полного понимания, и перейти к интуитивному, то видно, что функция fmap применяет функцию к значению сквозь f, и, как правило, так оно и есть.
Для наших нужд не надо полностью понимать всю силу функторов, давайте рассмотрим всего лишь списки:
instance Functor [] where
fmap = map
Тут полегче вышло — для списков, функция fmap полностью аналогична функции map. Ну а функцию map уже все императивщики знают, это применение функции ко всем членам списка. В Хаскеле она определяется очень просто:
map :: (a -> b) -> [a] -> [b]
map _ [] = []
map f (x:xs) = f x : map f xs
Смотрим на подпись: тут уже всё знакомо — функция от двух аргументов — функции одного параметра и списка. В результате получаем изменённый список.
Вторая строчка говорит, что для пустого списка, вне зависимости от функции ("_" — этим мы говорим, что нам не надо знать её значение) будет пустой список.
Для остальных случаев мы может список разделить на голову и остальную часть (x : xs, заметьте букву s, в английском это означает множественное число, мол много x-ов в xs) и вернуть другой список, где для головы мы применим функцию, а к хвосту мы рекурсивно применим нашу описываемую функцию.
map, но не до конца понимает, как можно сделать fmap = map — всё достаточно просто, замените f на []
fmap :: (a -> b) -> [] a -> [] b
Ну а это то же самое, что и
fmap :: (a -> b) -> [a] -> [b]
Что ж, переходим к нашему определению снова:
go = fmap ($ go) x
Что за функция с долларом? Неужели без Дяди Сэма и тут не обошлось? Ну что вы, это же чистый язык! $ — это обычная функция-оператор, называется аппликативная функция и определяется элементарно:
($) :: (a -> b) -> a -> b
f $ x = f x
Нет, вам не показалось, аппликативная функция ничего не делает, но зачастую её используют вместо скобок.
Хорошо, чтобы вас не смущать, перепишем функцию loeb, используя лямбда-выражения:
loeb :: Functor f => f (f a -> a) -> f a
loeb x = go
where
go = fmap (z -> z go) x
Читать лямбда выражения легко: z -> z go означает, что лямбда функция (слеш напоминает греческую букву лямбда — λ) от одной переменной z, ну а стрелочку -> читать как =
Отлично, мы смогли прочитать! Теперь осталось её понять!
Что loeb делает?
Короткая версия: loeb вычисляет результат в терминах самого себя, но это более сумашедше, чем то, что вы чувствовали, когда впервые услышали о рекурсии.
Подробная версия: А для чего loeb использовать? Где она пригодится? Например, можно сделать электронную таблицу (подобно Exel) для функтора списков — []:
xs :: [a]
xs = [...]
fs :: [[a] -> a]
fs = [...]
rs :: [a]
rs = [ f xs | f <- fs ] -- r = f xs
Пусть мы имеем список xs :: [a]. И имеем список функций, которые сворачивают списки к значениям, fs :: [[a] -> a]. Мы берём и для каждой функции из списка применяем к списку элементов, получая таким образом новое значение r. Соберём все r в список rs.
[ f xs | f <- fs ]
понять сложно, но всё же — мы в каждую ячейку списка применяем функцию (из списка) к списку значений, читается справа налево.
По этим действиям мы вычислили rs из списка значений xs и списка функций fs.
А теперь самая главная вещь — можно не брать список значений xs, а использовать rs вместо него. Другими словами, функция f применяется к списку результатов, которую сама и порождает!
fs :: [[a] -> a]
fs = [...]
rs :: [a]
rs = [ f rs | f <- fs ]
Конечно, это всё опирается на сильнейшую ленивость, пока вычисляется rs в терминах самого себя. Можно обе функции объединить, чтобы не иметь собственных определений fs, а они будут всего лишь параметром rs:
rs fs = [ f (rs fs) | f <- fs ]
Если присмотреться, то для списков rs = loeb
Таким образом, функция loeb берёт список функций, и вычисляет список результатов, которые он порождает, и применяет себя на только что порождённый список. Странно? Проверим? Закольцовано? Держу пари, нет!
Примеры с loeb
Пример, который поможет понять, как работать с этой функцией:
fs = [ const 1
, succ . (!! 0)
, succ . (!! 1)
, succ . (!! 2)
]
Тут const a _ = a — функция от двух переменных, которая всегда возвращает значение первого, succ x = inc инкремент для чисел (более точно, это обобщение инкремента для любых перечислимых значений), (!!) — функция вытаскивания n-элемента из списка, (.) — функциональная композиция 2-х функций, вначале применяет правую функцию, потом левую, в нашем случае, вначале вытаскивает элемент из списка, потом инкрементирует.
Тут мы описали список элементов в терминах предыдущих результатов. const 1 у нас первый элемент, и он всегда вернёт 1, после этого можно получить значение второго элемента — succ . (!! 0), и далее по цепочке — третий, четвёртый и пятый.
> loeb fs
[1,2,3,4]
Интересная часть состоит в том, что порядок совершенно необязательно должен быть с лева на право. Порядок можно вывернуть, главное, не достичь круговой рекурсии (в этом случае функция не сможет закончить вычисления).
fs = [ succ . (!! 1)
, succ . (!! 3)
, succ . (!! 0)
, const 1
]
> loeb fs
[3,2,4,1]
Правда же выглядит как электронная таблица?! Одно значение в ячейке известно, а остальные зависят друг от друга как-либо. Когда вычисление заканчивается, каждая ячейка имеет определённое значение. Это выглядит как обобщение комбинатора фиксированной точки.
Электронные таблицы!
Приведённый выше пример похож на одномерную таблицу. Но можно взять и другие функторы, которые ближе к реальности, массивы, например!
import Data.Array
import Data.List
import Control.Monad
import Text.Printf
loeb :: Functor f => f (f a -> a) -> f a
loeb x = go where go = fmap ($ go) x
-- Пустая клетка
e = val 0
-- Просто значение в клетке
val = const
-- Функция, которая возвращает (10 %) от выбранной клетки
vat ix = (* 0.1) . (! ix)
-- Сумма списка значений
sum' ixs = arr -> foldl' (acc ix -> acc + arr ! ix) 0 ixs
spreadsheet = listArray ((0,0), (4,4))
-- Prices | VAT | Effective prices + total
[ val 1, vat (0,0), sum' [(0,i) | i <- [0..1]], e, e
, val 3, vat (1,0), sum' [(1,i) | i <- [0..1]], e, e
, val 5, vat (2,0), sum' [(2,i) | i <- [0..1]], e, e
, val 2, vat (3,0), sum' [(3,i) | i <- [0..1]], e, e
, e, e, sum' [(i,2) | i <- [0..3]], e, e
]
printArr :: Array (Int, Int) Double -> IO ()
printArr arr =
forM_ [0..4] $ i -> do
forM_ [0..4] $ j ->
printf "%4.1f " (arr ! (i,j))
printf "n"
main = printArr $ loeb spreadsheet
Давайте запустим!
На выходе получим:
1.0 0.1 1.1 0.0 0.0
3.0 0.3 3.3 0.0 0.0
5.0 0.5 5.5 0.0 0.0
2.0 0.2 2.2 0.0 0.0
0.0 0.0 12.1 0.0 0.0
где в первой коленке у нас цены (используя val), во второй колонке у нас налоги того, что слева, в третьей колонке — эффективная цена, и ниже полная сумма всех эффективных цен. Теперь вы можете посмотреть, заказать и купить всё! Магия! :-)
Функция moeb
moeb — это результат игры с определением функции loeb: что если мы захотим абстрагироваться и от фукнции fmap. Для начала, это сделает подпись под функцией просто сумашедшей!
-- [m]oeb = multi-loeb :-)
moeb :: (((a -> b) -> b) -> c -> a) -> c -> a
moeb f x = go
where
go = f ($ go) x
И в новых терминах можно переопределить loeb, она будет лишь частным случаем moeb:
loeb = moeb fmap
А какие ещё можно использовать функции для параметра функции moeb, что бы её можно было использовать?
Ну например, если у нас есть фукнция
id :: a -> a
id x = x
Тогда:
moeb id x = id ($ moeb id x) x
= ($ moeb id x) x
= x (moeb id x)
-- Это то же самое, что и fix
-- fix f = f (fix f)
fix = moeb id
Как видим, moeb — это обобщение функции fix.
Есть и другие функции, которые можно применять в качестве параметров moeb, такие как traverse и foldMap, но я ещё не знаю для чего полезного можно это использовать.
Автор: Vitter