В булевой алгебре, используемой для моделирования работы цифровых схем, не учитывается время перехода (или инертность) логических элементов (например, «И», «ИЛИ») из одного состояния в другое (например, из 0 в 1). В случаях, когда время распространения сигнала внутри элемента достаточно мало, задержку перехода можно не учитывать. Но с повышением частоты изменения входных сигналов в реальных схемах начинает сказываться влияние времени распространения сигнала внутри ее элементов. Такие задержки могут порождать неустойчивую работу устройств (т.е. в сигналах после последовательного прохождения через узлы схемы появляются не учитываемые моделью схемы переходы, называемые сбоями). Многие производители современных процессоров держат в тайне, как они борются со сбоями, порождаемыми задержками, на частотах порядка ГГц. Ведь обычный проводник с множеством близких изгибов на плате в таком режиме работы уже превращается в индуктивность.
Чтобы проанализировать простейшие схемы на риски сбоя, обычно применяют метод временных диаграмм, ставший уже классическим. Сигналы в каждом узле прочерчиваются строго друг под другом; где нужно, производится искусственная задержка перехода из одного состояния в другое, а далее по булевому представлению строятся выходные сигналы. Данный метод не хорош тем, что требует работы с графиками, что может внести погрешность в получаемые сигналы. А нам нужно знать, возникнет ли сбой, и какой он будет иметь вид.
В 2005-м году я касался этой темы и изложил свои мысли в данной заметке на английском языке. Однако мой хороший знакомый посоветовал написать в Хабрахабр для обсуждения с пользователями.
В данном топике процедура анализа схем переведена из графического представления в математическое представление. При этом вводится в булеву алгебру параметр «время» посредством замены логических операций арифметическими. Для простоты анализа рассматриваются асинхронные, т.е. неуправляемые внешним (синхронизирующим или тактирующим) сигналом, цифровые схемы.
Начнем…
1. Переход от логического представления булевых функций к арифметическому представлению
Рассмотрим числовое множество 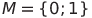 . На нем определены операции отрицания, конъюнкции, дизъюнкции и производимые от них (например, импликация, альтернативная дизъюнкция и др.). Выразим эти логические операции через арифметические на множестве M:
. На нем определены операции отрицания, конъюнкции, дизъюнкции и производимые от них (например, импликация, альтернативная дизъюнкция и др.). Выразим эти логические операции через арифметические на множестве M:
(1) 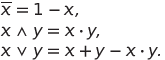
Покажем справедливость закона де Моргана 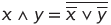 :
:
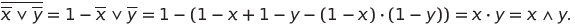
К выражениям (1) добавим правило
(2) 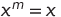
для всех натуральных значений m, справедливость которого очевидна.
Выражение для булевой функции, являющейся функцией входных сигналов схемы, теперь можно упростить по законам арифметических действий и правила (2). После упрощений перейти назад — к булевому представлению. При этом сам процесс минимизации можно автоматизировать, перейдя к символьным вычислениям.
2. Ввод в булеву алгебру параметра «время»
Как известно, единичная ступенчатая функция или функция Хевисайда определена на множестве действительных чисел и возвращает число, принадлежащее множеству M:
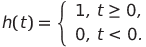
Обозначим через t текущее время. Заметим, что функцию h еще называют выключательной функцией. Очевидно следующее утверждение: любой сигнал в логической схеме, включающий переход из одного логического состояния в другое, можно представить как сумму-разность функций Хевисайда, взятых с соответствующим аргументом.
Для функции h имеет место очевидное правило
(3) 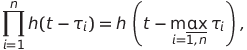
где 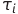 — момент времени, когда происходит изменение сигнала. Добавим правило (3) к (1) и (2).
— момент времени, когда происходит изменение сигнала. Добавим правило (3) к (1) и (2).
Теперь, зная аналитическое выражение для входных сигналов логической схемы, можно найти вид функции выходного сигнала.
3. Задержки в логических элементах схемы
Задержку сигнала в логическом элементе удобно моделировать как разность аргумента функции Хевисайда и длительности задержки (т.к. для существующих логических элементов в основном задержки по фронту (переход из 0 в 1) и спаду (переход из 1 в 0) примерно одинаковы). Таким образом, любой реальный логический элемент схемы можно моделировать как последовательное соединение звена «чистого» запаздывания по каждому входу и идеального логического элемента (здесь запаздывание равно длительности задержки). Например, уравнение выходного сигнала конъюнктора с задержкой 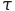 по входу имеет вид
по входу имеет вид
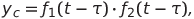
где 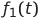 и
и 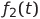 — функции, описывающие соответствующие входные сигналы.
— функции, описывающие соответствующие входные сигналы.
4. Алгоритм поиска сбойных состояний
Предлагаемый алгоритм поиска сбойных состояний аналогичен методу временных диаграмм; преимущество метода в том, что мы работаем не с графическими изображениями сигналов, а с их аналитическими выражениями (при этом появляется возможность аналитической оценки временных характеристик сбоя):
1. Пусть исследуемая схема функционирует в соответствии с некоторым логическим выражением, задаваемым ДНФ;
2. Задаемся функциями входных сигналов, представляющие собой переходы в таблице истинности, выражаемые через функцию Хевисайда;
3. Идем по пути следования сигналов в логической схеме с целью поиска выражения для выходного сигнала схемы, применяя правила (1) и (3);
4. Если в полученном выражении присутствует разность функций Хевисайда, то мы имеем статический сбой; если присутствует функция Хевисайда с задерживающим аргументом, то сбой динамический.
5. Пример анализа логической схемы.
Исследуем переход из набора 1111 в набор 1001 таблицы истинности для схемы, показанной на рис. 1.
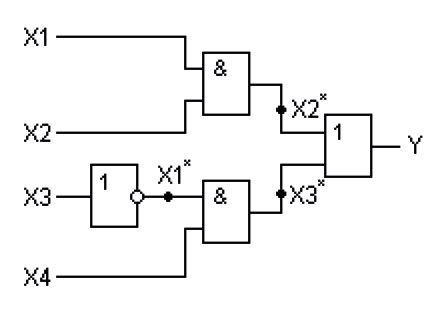
Рис. 1. Схема, реализующая булеву функцию 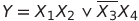 .
.
Представим входные сигналы следующим образом (для простоты будем рассматривать изменение состояний в момент времени, равный 5 временным единицам):
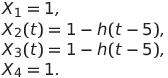
Предположим, что все элементы имеют одинаковые задержки, равные 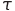 . Тогда
. Тогда
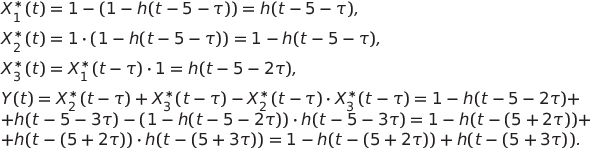
Таким образом, мы получили статический сбой — в результирующее выражение входит разность функций Хевисайда (рис. 2).
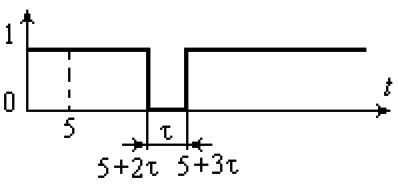
Рис. 2. График сигнала Y(t).
Заключение
В топике был рассмотрен метод анализа цифровых схем на риски сбоя, используя аналитическое представление сигналов внутри схемы. При этом пришлось произвести замену логических операций арифметическими. Переходы из одного состояния сигнала в другое описывались функцией Хевисайда. Достоинством описанной модификации метода временных диаграмм является то, что имеется возможность аналитического анализа характеристик сбоя.
Автор: pchelintsev_an