В далеком (а может и не очень далеком) 1975 году Альфред Ахо и Маргарет Корасик опубликовали статью, в которой был подробно описан алгоритм эффективного поиска всех вхождений всех строк-образцов в заданную строку. В дальнейшем этот алгоритм и получил название «алгоритм Ахо-Корасик». Неудивительно, что через некоторое время появились технические и «художественные» переводы данной статьи на русский язык. Порой мне даже встречались вольные изложения сути алгоритма в том виде, в котором его понимает автор. Причем последний, судя по тексту, узнал об алгоритме далеко не из первоисточника. Я не знаю существовал ли перевод, который послужил первоисточником проблемы, но мне всё больше и больше попадаются статьи с описанием алгоритма Ахо-Корасик, в котором допущена одна и та же кардинальная ошибка. Последней каплей была статья на хабре, которую данная ошибка не миновала. Собственно об этой ошибке мне и хотелось бы рассказать общественности в своей статье.
Перед началом, еще пара слов о целевой аудитории: Скорее всего, тем, кто давно знаком с алгоритмом Ахо-Корасик, моя статья будет не интересна, так как о его особенностях они давно уже знают. По крайней мере, все мои знакомые программисты не один раз применявшие данный алгоритм знают о существовании его неверных интерпретаций не понаслышке. А вот новичкам и тем, кому не довелось часто применять его на практике, эта статья может оказаться довольно полезной.
Итак, начнем.
Чтобы не тратить время читателей я упущу подробное описания алгоритма (это можно прочитать в оригинальной статье) и начну с примера и рисунка, дабы быстро пробежаться по терминам и разговаривать дальше «на одном языке».
Пусть мы будем искать следующий список строк-образцов: {«HE», «SHE», «HIS», «HER»}. Первым делом нам надо построить автомат. Тот самый конечный автомат с состояниями и переходами, на базе которого строится алгоритм Ахо-Корасик. Черным кружком обозначим начальное состояние автомата. Синими кружками будем обозначать очередное состояние автомата, достижение которого не означает факт обнаружения строки-образца. И, наконец, синие кружки с перекрестием – это очередное состояния автомата, достижение которого означает факт обнаружения строки-образца. Естественно между ними тянуться переходы – черные стрелки подписанные буквами, которые являются условием перехода. Их будем называть главными переходами. При отсутствии главного перехода для очередного входного символа автомат переходит в начальное состояние. Назовем их нулевыми переходами. Эти переходы я специально не указываю, чтобы не загромождать рисунок. Про нулевые переходы стоить отметить то, что при переходе по ним входной символ не поглощается, то есть остается во входной строке и после перехода снова будет использован. Исключением является нулевой переход из начального состояния, где, по сути, состояние не меняется, а входной символ поглощается.
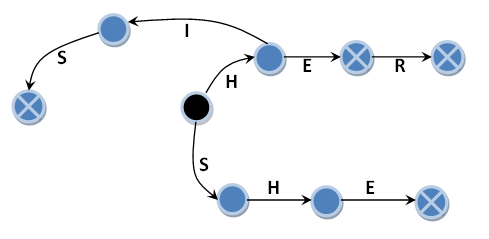
На рисунке изображены четыре синих кружка с перекрестием, каждый из которых соответствует одной из строк образцов. На самом деле уже в этом примере заложена та самая ошибка. Оригинальный алгоритм описывает автомат немного иначе. Но обо всем по порядку.
Вспомним о так называемых суффиксных ссылках. Это такие переходы, которые указывают, в какое состояние необходимо перейти, если для очередного символа входной строки нет главного перехода. На следующем рисунке они указаны пунктирными черными стрелками. Будем называть их суффиксными переходами или суффиксными ссылками. Переход по суффиксным ссылкам по аналогии с нулевым переходом не поглощает входной символ. Как и в первом случае, переходы, ведущие на начальное состояние при отсутствии главного перехода, я не изображаю.

В примере без суффиксных ссылок, но с нулевыми переходами, в строке “HERHEHIS” будут найдены все вхождения (“HE”, “HER”, “HE”, “HIS”). Но во входной строке “HISHER” будут найдены лишь три вхождения (“HIS”, “HE”, “HER”) и автомат не обнаружит вхождения строки-образца “SHE”, в чём легко убедиться. В случае же с суффиксными ссылками для строки “HERHEHIS” результат будет тот же, а для строки “HISHER” результатом станет список из четырех найденных вхождений: (“HIS”, “SHE”, “HE”, “HER”). То есть в последнем случае были найдены все вхождения. Нет, нет, это не та ошибка, о которой я хотел рассказать. Ни в коем случае так не подумайте. Чтобы кто-то забыл о суффиксных ссылках, такого я еще не видел. Всё еще впереди.
Я не стал в подробностях описывать алгоритм построения автомата, но алгоритм поиска для описанных выше случаев рассмотрим подробнее. Для этого с целью удобства приведем для начала автомат без суффиксных ссылок, в котором пронумеруем его состояния (синие цифры возле соответствующих кружков).
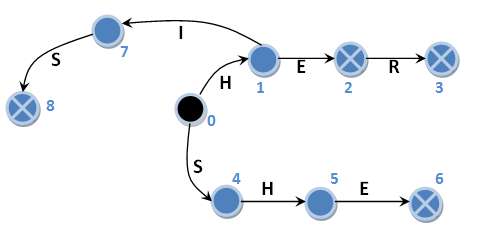
Да, кстати, напомню, что, не смотря на отсутствие суффиксных ссылок, этот автомат переходит в начальное состояние при отсутствии главного направления с сохранением входного символа. На рисунке эти переходы не изображены. Приступим. Начальное состояние 0, входная строка “HERHEHIS”:
0 H -> 1 ERHEHIS
1 E -> 2 RHEHIS (“HE”)
2 R -> 3 HEHIS (“HER”)
3 H -> 0 HEHIS //главного направления нет, переходим в начальное состояние с сохранением входного символа
0 H -> 1 EHIS
1 E -> 2 HIS (“HE”)
2 H -> 0 HIS //главного направления снова нет
0 H -> 1 IS
1 I -> 7 S
7 S -> 8 (“HIS”)
Вот и они — все четыре вхождения. Проделаем теперь аналогичное со строкой “HISHER”:
0 H -> 1 ISHER
1 I -> 7 SHER
7 S -> 8 HER (“HIS”)
8 H -> 0 HER
0 H -> 1 ER
1 E -> 2 R (“HE”)
2 R -> 3 (“HER”)
Как и ожидалось, были найдены лишь три вхождения. Теперь можно вникнув в суть примеров и сформулировать следующее утверждение: «В автомате без суффиксных ссылок для входной строки содержащих перекрывающиеся строки-образцы будут найдены не все вхождения». Речь идет именно о перекрывающихся (“HIS” и “SHE” в “HISHE”), а не входящих одна в другую (“HE” и “HER” в “HER”).
В автомате с суффиксными ссылками такого, конечно же, не происходит. Проверим на тех же примерах. Пронумеруем состояния автомата с суффиксными ссылками:
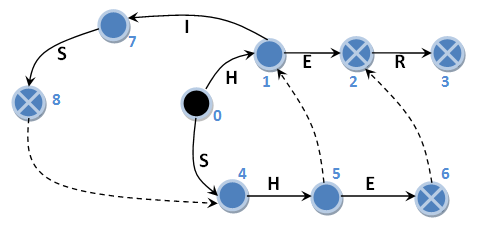
Берем входную строку “HERHEHIS”:
0 H -> 1 ERHEHIS
1 E -> 2 RHEHIS (“HE”)
2 R -> 3 HEHIS (“HER”)
3 H -> 0 HEHIS //главного направления и суффиксных ссылок нет
0 H -> 1 EHIS
1 E -> 2 HIS (“HE”)
2 H -> 0 HIS //главного направления и суффиксных ссылок нет
0 H -> 1 IS
1 I -> 7 S
7 S -> 8 (“HIS”)
Для данной входной строки ход работы автомата точно такой же, как и для автомата без суффиксных ссылок. Теперь подсунем автомату строку “HISHER”:
0 H -> 1 ISHER
1 I -> 7 SHER
7 S -> 8 HER (“HIS”)
8 H -> 4 HER //переход по суффиксной ссылке
4 H -> 5 ER
5 E -> 6 R (“SHE”)
6 R -> 2 R (“HE”) //переход по суффиксной ссылке
2 R -> 3 (“HER”)
Действительно, были обнаружены все четыре вхождения. Что здесь можно сформулировать: «Без суффиксных ссылок надежда найти все вхождения строк-образцов стремиться к нулю».
Нередко я встречал описания алгоритма Ахо-Корасик, которое заканчивалось именно на этом. Подробно расписывался алгоритм построения дерева, а про алгоритм поиска писалось: «он элементарен – ходим по состояниям и выдаем результат». И авторы этих произведений были бы абсолютно правы, если бы не ошибались. Для начала покажу пример, с которым не справится даже автомат с суффиксными ссылками. Построим аналогичный автомат, но введём в него две дополнительных строки-образца: “I” и “IS”. Схематично такой автомат с его главными и суффиксными переходами можно изобразить следующим образом:
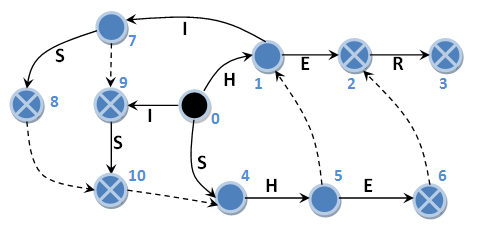
В качестве входной строки возьмем всю ту же известную нам “HISHER”. Итак, поехали:
0 H -> 1 ISHER
1 I -> 7 SHER
7 S -> 8 HER (“HIS”)
8 H -> 10 HER (“IS”)
10 H -> 4 HER
4 H -> 5 ER
5 E -> 6 R (“SHE”)
6 R -> 2 R (“HE”)
2 R -> 3 (“HER”)
Итого имеем пять найденных вхождений. Но среди них нет строки-образца “I”. В чем же дело? Как так получилось? На самом деле всё элементарно. При переходе по суффиксной ссылке мы миновали состояние 9, которое могли посетить только из состояний 7 и 0. Следовательно, везде, где есть подстрока “HIS”, строка-образец “I” найдена не будет. Аналогично, во входной строке “HISHER” мы бы нашли строку-образец “Н” только один раз, предварительно добавив её в список и построив соответствующий автомат. И дело здесь не в том, что строки “I” и “H” состоят из одного символа. Проверьте сами: замените в списке “HIS” на “HIPS”, “IS” на “IPS”, “I” на “IP”, и подайте на автомат входную строку “HIPSHER”. Строка-образец “IP” найдена не будет по тем же самым причинам. Так что же было не так: строение автомата или алгоритм поиска?
У вариантов решения данной проблемы выделяется один явный фаворит. Столкнувшись с похожим примером и разобравшись в чем причина, разработчики выбирают наиболее очевидное лобовое решение: «после перехода по суффиксной ссылке пробегать обратно по главным переходам до начального состояния». Действительно, это избавляет нас от проблемы, и такая реализация вполне имеет право на жизнь. Здесь можно отметить только два но:
- Оценка сложности алгоритма (его временных затрат) меняется в худшую сторону;
- Никакой проблемы на самом деле не было.
Для тех, кто знаком с оригинальной статьей или хотя бы с корректным её переводом, могли обнаружить ошибку еще в самом первом автомате. Если для некоторого состояния записывать факт обнаружения не только полной (от начального состояния) найденной строки-образца, но и все её суффиксы которые тоже являются строками-образцами, то все будет работать корректно.
Приведу еще раз схему последнего рассмотренного автомата с некоторыми изменениями.
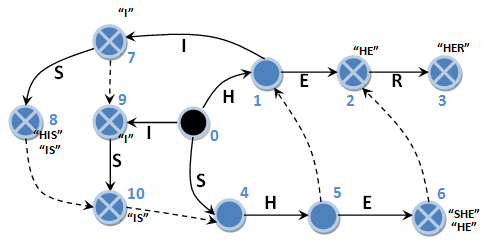
При достижении состояния 6 мы фиксируем вхождения “SHE” и “HE”. Именно на состоянии 6, а не после перехода по суффиксной ссылке. Аналогично, состояние 7 будет фиксировать вхождение строки-образца “I”, а состояние 8 – “HIS” и “IS”. В алгоритме поиска придется в таком случае убрать фиксацию вхождения после перехода по суффиксной ссылке, иначе одно и то же вхождение будет зафиксировано дважды. Например, после перехода с 6-го состояния на 2-е фиксировать вхождение “HE” не нужно, мы это сделали ранее после перехода с 5-го состояния на 6-е. Теперь не нужен никакой обратный проход до начального состояния. Поиск действительно прост и незамысловат. Разбор входной строки “HISHER” теперь будет выглядеть так:
0 H -> 1 ISHER
1 I -> 7 SHER (“I”)
7 S -> 8 HER (“HIS”, “IS”)
8 H -> 10 HER
10 H -> 4 HER
4 H -> 5 ER
5 E -> 6 R (“SHE”, “HE”)
6 R -> 2 R
2 R -> 3 (“HER”)
Отлично, теперь все 6 вхождений обнаружены. Кому-то может показаться, что это усложняет построение автомата, но это совсем не так. Будет не сложнее чем предыдущий наш пример. Я не описывал алгоритм построения автомата с самого начала, поэтому и сейчас его приводить не буду. Он прекрасно описан в оригинальной статье Альфреда Ахо и Маргарет Корасик, которую, возможно, кому-то стоит прочесть.
В заключении, хотелось бы посоветовать тем, кто читает что-то не из первоисточника всё же отдавать себе отчет в его возможной некорректности. И по возможности добираться до истины, прежде чем допустить очередную ошибку в реализации. А тем, кто пишет «адаптированные» изложения – относитесь к своему труду более ответственно, не вводя в заблуждение остальных.
Автор: leshiysoft

