Мне всегда нравилось, когда заголовок однозначно говорит о том, что будет дальше, например, «Техасская резня бензопилой». Поэтому под катом мы действительно будем добавлять пространственный поиск к СУБД, в которой его изначально не было.
Вводная
Попробуем обойтись без общих слов про важность и полезность пространственного поиска.
На вопрос, почему было не взять открытую СУБД с уже встроенным пространственным поиском, ответ будет такой: «хочешь сделать что-то хорошо, делай это сам»(С). А если серьезно, мы попробуем показать, что большинство практических пространственных задач может быть решено на на вполне рядовом десктопе без перенапряжения и особых затрат.
В качестве подопытной СУБД будем использовать открытую редакцию OpenLink Virtuoso. В её платной версии доступна пространственная индексация, но это совсем другая история. Почему именно эта СУБД? Автору она нравится. Быстрая, легкая, мощная. Скопировал-запустил-все работает. Будем пользоваться только штатными средствами, никаких С-плагинов или специальных сборок, лишь официальная сборка и текстовый редактор.
Тип индекса
Будем индексировать точки с помощью pixel-code (блочного) индекса.
Что за pixel-code индекс? Это компромиссный вариант заметающей кривой, позволяющий работать с неточечными объектами в 2-мерном поисковом пространстве. Объединим в данный класс все методы, которые:
- Некоторым образом делят пространство поиска на блоки
- Все блоки нумеруются
- Каждому индексируемому объекту присваивается один или несколько номеров блоков, в которых он расположен
- При поиске экстент расщепляется на блоки и для каждого блока или непрерывной цепочки блоков из обычного целочисленного индекса (B-дерево) достаются все объекты, которые им принадлежат.
Наиболее известными методами являются:
- Старый добрый Igloo (или другая заметающая кривая) ограниченной точности. Пространство разрезается решеткой, шагом которой (обычно) является характерный размер индексируемого объекта. Ячейки нумеруются как X…xY…yZ…z… т.е. склеиванием номеров ячеек по нормалям.
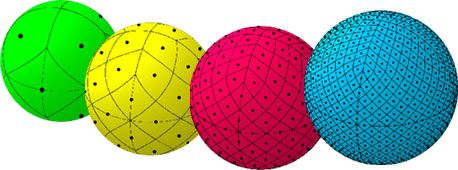
- HEALPix. Название происходит от Hierarchical Equal Area iso-Latitude Pixelisation. Этот метод предназначен для разбиения сферической поверхности с целью избежать основного недостатка Igloo – разной площади под ячейками на разной широте. Сфера разделяется на 12 равных по площади участков, каждый из которых в дальнейшем иерархически делится на 4 под — участка. Иллюстрация к этому методу вынесена в шапку статьи
- Hierarchical Triangular Mesh (HTM).Это схема последовательного приближения к сфере с помощью треугольников, начиная с 8 стартовых, каждый из которых иерархически разбивается на 4 под — треугольника
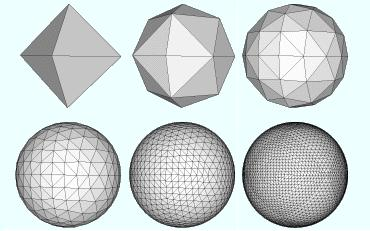
- Одной из наиболее известных схем блочных индексов, является GRID. Пространственные данные рассматриваются как частный случай многомерного индекса. При этом:
- пространство режется на части с помощью решетки
- получившиеся ячейки некоторым образом нумеруются
- данные, попавшие в конкретную ячейку, хранятся вместе
- значения атрибутов переводятся в номера ячеек по осям с помощью “директории”, предполагается, что она невелика и размещается в памяти
- если “директория” велика, она разбивается на уровни a la дерево
- при изменении, решетка может адаптироваться, ячейки или столбцы расщепляться или, наоборот, сливаться
3-уровневый GRID, основанный на Z-order используется DB2, 4-уровневый GRID, основанный на варианте кривой Гильберта использован в MS SQLServer 2008
При всех минусах, главным из которых, пожалуй, является неадаптивность, необходимость настраивать индекс под конкретную задачу, у блочных индексов есть и плюсы: простота и всеядность. В сущности это это обычное дерево с дополнительной семантической нагрузкой. Мы каким-то образом преобразуем геометрию в числа при индексации и тем же самым способом получаем ключи для поиска в индексе.
В данной работе мы будем использовать Igloo из-за простоты: координаты в номер можно дешево преобразовать средствами PL/SQL. Использовать HTM или кривую Гильберта без привлечения С-плагинов было бы затруднительно.
Тип данных
Почему точки? Как уже отмечалось, Блочным индексам всё равно, что индексировать. При этом растеризатор для точек тривиален, а для полигонов его пришлось бы писать, причем это совершенно не важно для раскрытия темы.
Собственно данные
Не мудрствуя лукаво,
- посадим точки на узлы решетки 4000Х4000 с началом в (0,0) и шагом 1.
- получим квадрат из 16 млн точек.
- ячейку блочного индекса примем за 10Х10,
- таким образом у нас 400Х400 ячеек в каждой по 100 точек.
Для индекса не важно, как точки расположены внутри ячейки, а нам такая регулярность позволит контролировать корректность результатов.
Для генерации данных будем использовать вот такой скрипт на AWK(пусть, будет 'data.awk'):
BEGIN {
cnt = 1; sz = 4000;
# Set the checkpoint interval to 100 hours -- enough to complete most of experiments.
print"checkpoint_interval (6000);";
print"SET AUTOCOMMIT MANUAL;";
for (i=0; i < sz; i++) {
for (j=0; j < sz; j++) {
print "insert into "xxx"."YYY"."_POINTS"";
print " ("oid_","x_", "y_") values ("cnt","i","j");";
cnt++;
}
print"commit work;"
}
print"checkpoint;"
print"checkpoint_interval (60);";
exit;
}
Сервер
- Возьмем официальный билд с сайта компании.
Автор использовал последнюю версию 7.0.0 (x86_64), но это не принципиально, можно взять любую другую. - Устанавливаем, если нет, Microsoft Visual C++ 2010 Redistributable Package (x64)
- Выбираем директорию для опытов и копируем туда libeay32.dll, ssleay32.dll, isql.exe, virtuoso-t.exe из архивной 'bin' и virtuoso.ini из архивной 'database '
- Запускаем сервер с помощью 'start virtuoso-t.exe +foreground', разрешаем файерволу открыть порты
- Тестируем доступность сервера командой 'isql localhost:1111 dba dba'. После установления соединения вводим, например. 'select 1;' и убеждаемся, что сервер жив.
Схема данных
Для начала создадим таблицу точек, ничего лишнего:
create user "YYY";
create table "xxx"."YYY"."_POINTS" (
"oid_" integer,
"x_" double precision,
"y_" double precision,
primary key ("oid_")
);
Теперь собственно индекс:
create table "xxx"."YYY"."_POINTS_spx" (
"node_" integer,
"oid_" integer references "xxx"."YYY"."_POINTS",
primary key ("node_", "oid_")
);
где node_ — идентификатор ячейки пространства. Обратим внимание, что, хотя, индекс создается как таблица, оба поля присутствуют в первичном ключе и, следовательно, упакованы в дерево.
Настраиваем параметры индекса:
registry_set ('__spx_startx', '0');
registry_set ('__spx_starty', '0');
registry_set ('__spx_nx', '4000');
registry_set ('__spx_ny', '4000');
registry_set ('__spx_stepx', '10');
registry_set ('__spx_stepy', '10');
Системная функция registry_set позволяет записывать строковые пары имя/значение в системный реестр — это намного быстрее, чем держать их во вспомогательной таблице и все еще покрыто транзакциями.
Триггер на запись:
create trigger "xxx_YYY__POINTS_insert_trigger" after insert
on "xxx"."YYY"."_POINTS"
referencing new as n
{
declare nx, ny integer;
nx := atoi (registry_get ('__spx_nx'));
declare startx, starty double precision;
startx := atof (registry_get ('__spx_startx'));
starty := atof (registry_get ('__spx_starty'));
declare stepx, stepy double precision;
stepx := atof (registry_get ('__spx_stepx'));
stepy := atof (registry_get ('__spx_stepy'));
declare sx, sy integer;
sx := floor ((n.x_ - startx)/stepx);
sy := floor ((n.y_ - starty)/stepy);
declare ixf integer;
ixf := (nx / stepx) * sy + sx;
insert into "xxx"."YYY"."_POINTS_spx" ("oid_","node_")
values (n.oid_,ixf);
};
Кладем все это в, например, 'sch.sql' и исполняем посредством
isql.exe localhost:1111 dba dba <sch.sql
Загрузка данных
После того, как схема готова, можно заливать данные.
gawk -f data.awk | isql.exe localhost:1111 dba dba >log 2>errlog
Заняло это у автора 45 минут (~6000 в секунду) на Intel i7-3612QM 2.1GHz c 8Gb памяти.
Размер памяти, занятый при этом сервером, был около 1 Gb, размер базы на диске — 540Mb, т.е. ~34 байт на точку и ее индекс.
Теперь следует убедиться, что результат корректен, вводим в isql
select count(*) from "xxx"."YYY"."_POINTS";
select count(*) from "xxx"."YYY"."_POINTS_spx";
Оба запроса должны выдать 16 000 000.
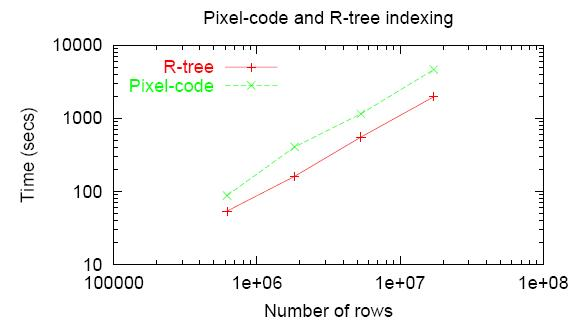
Как ориентир можно использовать данные, опубликованные здесь:
 .
.
Получены они на PostgreSQL(Linux), 2.2GHz Xeon.
С одной стороны, данные получены 9 лет назад. С другой, в данном случае, узким местом являются дисковые операции, а случайный доступ к диску за истекший период ускорился не столь уж значительно.
А вот здесь мы можем почерпнуть, что время пространственной индексации соизмеримо с временем заливки собственно данных.
Следует отметить, что заливка данных с последующей индексацией происходит (по очевидным причинам) существенно быстрее, нежели индексация на лету. Но нас более будет интересовать именно индексация на лету т.к. для практических целей более интересна пространственная СУБД, а не пространственная поисковая система.
И еще, нельзя не отметить, что при заливке пространственных данных очень важен порядок их заливки.
И в данной работе и в упомянутой выше порядок подачи точек был идеальным (или близким к нему) с точки зрения пространственного индекса. Если данные перемешать, производительность упадет весьма драматично вне зависимости от выбранной СУБД.
Если данные приходят произвольно, можно порекомендовать накапливать их в отстойнике, по мере его переполнения сортировать и заливать порциями.
Налаживаем поиск
Для этого воспользуемся такой замечательной особенностью Virtuoso, как процедурные view.
create procedure "xxx"."YYY"."_POINTS_spx_enum_items_in_box" (
in minx double precision,
in miny double precision,
in maxx double precision,
in maxy double precision)
{
declare nx, ny integer;
nx := atoi (registry_get ('__spx_nx'));
ny := atoi (registry_get ('__spx_ny'));
declare startx, starty double precision;
startx := atof (registry_get ('__spx_startx'));
starty := atof (registry_get ('__spx_starty'));
declare stepx, stepy double precision;
stepx := atof (registry_get ('__spx_stepx'));
stepy := atof (registry_get ('__spx_stepy'));
declare sx, sy, fx, fy integer;
sx := floor ((minx - startx)/stepx);
fx := floor (1 + (maxx - startx - 1)/stepx);
sy := floor ((miny - starty)/stepy);
fy := floor (1 + (maxy - starty - 1)/stepy);
declare mulx, muly integer;
mulx := nx / stepx;
muly := ny / stepy;
declare res any;
res := dict_new ();
declare cnt integer;
for (declare iy integer, iy := sy; iy < fy; iy := iy + 1)
{
declare ixf, ixt integer;
ixf := mulx * iy + sx;
ixt := mulx * iy + fx;
for select "node_", "oid_" from "xxx"."YYY"."_POINTS_spx"
where "node_" >= ixf and "node_" < ixt do
{
dict_put (res, "oid_", 0);
cnt := cnt + 1;
}
}
declare arr any;
arr := dict_list_keys (res, 1);
gvector_digit_sort (arr, 1, 0, 1);
result_names(sx);
foreach (integer oid in arr) do
{
result (oid);
}
};
create procedure view "xxx"."YYY"."v_POINTS_spx_enum_items_in_box" as
"xxx"."YYY"."_POINTS_spx_enum_items_in_box" (minx, miny, maxx, maxy) ("oid" integer);
В сущности эта процедура устроена очень просто, она выясняет, в какие ячейки блочного индекса попадает поисковый экстент и для каждой строчки этих ячеек делает под-запрос, записывает идентификаторы записей в хэш-мапу, устраняя при этом дубликаты и отдает получившийся набор идентификаторов как результат.
Как же воспользоваться пространственным индексом? Например, так:
select count(*), avg(x.x_), avg(x.y_) from
"xxx"."YYY"."_POINTS" as x, "xxx"."YYY"."v_POINTS_spx_enum_items_in_box" as a
where a.minx = 91. and a.miny = 228. and a.maxx = 139. and a.maxy = 295.
and x."oid_" = a.oid
and x.x_ >= 91. and x.x_ < 139. and x.y_ >= 228. and x.y_ < 295.;
Здесь делается join между таблицей точек и синтетическим рекордсетом из процедурного view по идентификаторам. Здесь процедурное view выполняет роль грубого фильтра, который работает с точностью до ячейки. Поэтому в последней строке мы поместили тонкий фильтр.
Ожидаемый результат:
- Число: (139 — 91) * (295 — 228) = 3216
- Среднее по X: (139 + 91 — 1) / 2 = 114.5 (-1 т.к. правая граница исключена)
- Среднее по Y: (295 + 228 — 1) / 2 = 261 (...)
Вот так вот одним запросом в пределах одной транзакции мы и выполнили пространственный поиск.
Benchmark
Для приготовления потока запросов воспользуемся следующим скриптом на AWK:
BEGIN {
srand();
for (i=0; i < 100; i++) {
for (j=0; j < 100; j++) {
startx = int(rand() * 3900);
finx = int(startx + rand() * 100);
starty = int(rand() * 3900);
finy = int(starty + rand() * 100);
print "select count(*), avg(x.x_), avg(x.y_) from";
print ""xxx"."YYY"."_POINTS" as x, "
print ""xxx"."YYY"."v_POINTS_spx_enum_items_in_box" as a"
print "where a.minx = "startx". and a.miny = "starty"."
print " and a.maxx = "finx". and a.maxy = "finy". and"
print "x."oid_" = a.oid and x.x_ >= "startx". and x.x_ < "finx"."
print " and x.y_ >= "starty". and x.y_ < "finy".;"
}
}
exit;
}
Как видим, получается 10 000 запросов в случайных местах случайного размера (0...100). Приготовим 4 таких набора и выполним три серии тестов — запускаем один isql с тестами, 2 параллельно и 4 параллельно. На восьмиядерном процессоре больше распараллеливать смысла нет. Замерим производительность.
- 1 поток: 151 sec = ~66 запросов в секунду на поток
- 2 потока: 159 sec = ~63…
- 4 потока: 182 sec = ~55…
Можно попробовать сравнить эти времена с оными, полученными спинномозговым путем посредством двух обычных индексов — по x_&y_. Проиндексируем таблицу по этим полям и запустим аналогичную серию тестов с запросами типа
select count(*), avg(x.x_), avg(x.y_) from
"xxx"."YYY"."_POINTS" as x
where x.x_ >= 91. and x.x_ < 139. and x.y_ >= 228. and x.y_ < 295.;
Результат таков: серия из 10 000 запросов выполняется за 417 секунд, имеем 24 запроса в секунду.
Заключение
Представленный метод имеет ряд недостатков, главным из которых, как уже отмечалось, является необходимость настраивать его на конкретную задачу. Его производительность сильно зависит от параметров настройки, которые уже нельзя поменять после создания индекса. Впрочем, это справедливо для большинства пространственных индексов вообще.
Но даже такой написанный на коленке индекс дает сносную производительность. Кроме того, раз уж мы полностью контролируем процесс, на этой основе можно делать белее сложные конструкции, например, много-табличные индексы, построить которые штатными методами затруднительно. Но об этом как-нибудь в следующий раз.
Автор: zzeng






