Меня давно занимал вопрос: «а что, если попробовать прогнать цифровую запись песни через преобразование Фурье, посмотреть зависимость спектра от времени и попытаться вытащить из полученной информации аккорды песни?». Вот, наконец, нашел время попробовать…
Итак, постановка задачи:
Есть файл с оцифрованной музыкой (не MIDI!), для определенности mp3. Надо определить последовательность смены аккордов, образующую гармонию произведения. Под «музыкой» будем подразумевать типичную европейскую музыку — 12 полутонов в октаве, гармония в основном на основе мажорных/минорных трезвучий, допустимы также уменьшенные и увеличенные трезвучия и *sus2/*sus4 (аккорды со 2-й/4-й ступенью вместо 3-й).
Немного теории
Ноты в европейской музыке представляют собой звуки с частотами из фиксированного набора (об этом чуть ниже), при этом звуки, отличающиеся частотой в 2, 4, 8… раз обозначаются одной нотой. Музыкальные интервалы являются фиксированными соотношениями частот двух нот. Устроена эта интервальная система так:
- интервал f1 / f2 == 2 называется октавой
- октава делится на 12 равных (в «логарифмическом» смысле) минимальных интервалов, называемых малыми секундами или полутонами. Если ноты n1 и n2 составляют малую секунду, то их частоты f1 и f2 соотносятся как
f2 / f1 = 21/12. Две малых секунды составляют большую секунду, три — малую терцию, четыре — большую терцию, семь – квинту. Остальные интервалы нам не понадобятся.
Буквенные обозначения нот в принятой у нас в России нотации такие:
A — ля, B — си-бемоль, H — си, C — до, D — ре, E — ми, F — фа, G — соль.
# (диез) обозначает повышение частоты на 1/2 тона, b (бемоль) — понижение на 1/2 тона. На октаву из 12 полутонов ноты отображаются так:
A B H C C#/Db D D#/Eb E F F#/Gb G G#/Ab
Октавы имеют хитрые названия и номера, но нам это не интересно, достаточно знать что частота ноты «ля» первой октавы равна 440 Гц. Частоты остальных нот легко посчитать, исходя из написанного выше.
Аккорд представляет собой несколько одновременно звучащих нот. При этом они могут извлекаться последовательно (арпеджио, оно же «перебор» на жаргоне дворовых гитаристов), но, поскольку звук затихает не сразу, ноты успевают какое-то время позвучать вместе. В европейской традиции наиболее распространены аккорды из трех звуков (собственно трезвучия). Обычно используются мажорные и минорные трезвучия. В мажорных аккордах 1-я (начиная с самой низкой) и 2-я ноты образуют большую терцию, а 2-я и 3-я — малую, в минорных, наоборот, 1-я и 2-я — малую, 2-я и 3-я — большую. 1-я и 3-я ноты в обоих случаях образуют квинту. Так же встречаются уменьшенные (две малых терции) и увеличенные (две больших терции) трезвучия, а в рок-музыке достаточно распространены sustained-аккорды (не знаю, как они по-русски) — sus2 со 2-й нотой на 1/2 тона ниже, чем у минорного и sus4 со 2-й нотой на 1/2 тона выше, чем у мажорного. 3-я нота в обоих вариантах sustained-аккорда образует с 1-й обычную квинту.
В одном музыкальном произведении редко когда в одинаковой мере используются все 12 нот. Как правило, существует «базовое» подмножество из 7 нот, и ноты берутся в основном из него. Такое подмножество можно определить при помощи маски из 0 и 1, накладываемой на вектор из 12 нот. Если утрировать, такое подмножество называется тональностью, а множество всех возможных циклических сдвигов маски тональности — ладом. В европейской музыке в основном используются два лада:
- мажор с маской 1 0 1 0 1 1 0 1 0 1 0 1
- минор с маской 1 0 1 1 0 1 0 1 1 0 1 0
Аккорды, используемые в конкретной тональности, строятся по возможности из нот этой тональности.
Можно заметить, что маски мажора и минора отличаются с точностью до сдвига. Соответственно, аккорды, например в до-мажоре и соответствующем ему ля-миноре используются одни и те же (это мы так ненавязчиво вернулись к нашей задаче).
Нота, «начиная с которой» накладывалась маска, называется тоникой. Номер ноты, входящей в тональность, начиная с тоники, называется ступенью. Когда говорят о структуре конкретного аккорда, ступени считают от его 1-й ноты (т.н. основного тона).
Аккорды традиционно обозначаются символом его основного тона, к которому справа без пробела приписывается суффикс типа аккорда. На примере ноты A (ля):
- A — мажорное трезвучие
- Am — минорное трезвучие
- A5+ — увеличенное трезвучие (у него есть другое, официальное обозначение, но мне чаще попадалось такое)
- Am5- — уменьшенное трезвучие (опять же, есть другие обозначения)
- Asus2 — sustained со второй ступенью
- Asus4 — sustained с четвертой ступенью
[Оффтопик для тех, кто учился в «музыкалке»] Я слыхал про отличия мелодического и гармонического миноров и про проблемы темперации (возвращаясь назад к корням 12-й степени) тоже. Но, как мне кажется, в рамках данной статьи достаточно вышеприведенного упрощенного описания предметной области.
Переходим к практике
Итак, нам надо:
- распаковать mp3 в массив чисел, представляющий собой график зависимости амплитуды звука от времени
- определить, какие ноты звучат в каждый конкретный момент времени
- определить, какие аккорды образуют эти ноты
С первой задачей я возиться не стал — взял готовый конвертер звука sox, поддерживающий и mp3, и «сырые» форматы, где звук хранится как раз как график зависимости амплитуды от времени. В *nix-системах он ставится тривиально с помощью пакетного менеджера — у меня на Ubuntu это выглядит так:
$ sudo apt-get install sox
$ sudo apt-get install lame
Вторая строчка ставит LAME mp3 encoder.
Под виндой sox можно скачать с официального сайта, но потом придется несколько помучиться с поиском в интернете подходящих DLL-ек LAME.
Со второй задачей, в принципе, все просто. Для того, чтобы понять, какие ноты звучат в конкретный момент времени, необходимо выполнить спектральный анализ кусочка нашего массива с амплитудами в диапазоне индексов, соответствующем небольшой окрестности этого момента. В результате спектрального анализа мы получим амплитуды для множества частот, «составляющих» анализируемый кусочек звука. Надо отфильтровать частоты, выделив те из них, которые близки к частотам нот, и отобрать из них самые большие — они соответствуют самым громким нотам. Я говорю «близки», а не «равны», потому что в природе не бывает идеально настроенных музыкальных инструментов; особенно это относится к гитарам.
Для спектрального анализа дискретного представления изменяющегося во времени сигнала можно воспользоваться оконным быстрым преобразованием Фурье. Я содрал с просторов интернета простейшую не оптимизированную реализацию БПФ, перевел ее с C++ на Scala, в качестве оконной функции взял функцию Ханна. Подробнее об этом всем можно почитать в соответствующих статьях Википедии.
После получения массива амплитуд по частотам отбираем частоты в окрестности (по умолчанию ее размер 1/4 полутона) вокруг частоты каждой ноты в некотором диапазоне октав (опыт показывает, что лучше всего анализировать октавы с большой по вторую или третью). В каждой такой окрестности вычисляем максимум амплитуды и считаем его громкостью соответствующей ноты. После этого суммируем «громкости» каждой ноты по всем октавам и, наконец, делим все элементы полученного массива из 12 «громкостей» на значение его максимального элемента. Полученный вектор из 12 элементов в разных источниках называется хромограммой (chromagram).
Тут нельзя не упомянуть о паре тонкостей. Во-первых, для разных произведений удобный диапазон октав для анализа разный — например, вступление к My Friend Of Misery Металлики играется, судя по всему, на бас-гитаре и звучит довольно низко; в верхних октавах там присутствуют большей частью обертона и левые частоты от дисторшена, которые только мешают.
Во-вторых, в природе не бывает идеально настроенных гитар. Вероятно, это связано с тем, что струны в зависимости от лада по-разному удлиняются при зажимании (ну и вообще, пальцы давят на них неравномерно). Кроме того, инструмент сей быстро расстраивается в процессе игры на оном. Например, в акустических записях Летова с настройкой полный финиш — ну это-то можно понять. А вот почему в той же My Friend Of Misery одна не-помню-какая нота стабильно звучит ровно на четверть тона не то выше, не то ниже — загадка. И даже у хорошо настроенных гитар на записях всевозможных квартирников строй обычно не совпадает с каноническим по общей высоте — т.е. «ля» первой октавы может быть не совсем 440 герц.
Для нейтрализации таких косяков пришлось предусмотреть в программе возможность компенсации общего сдвига строя. А вот с расстроенностью отдельных струн и в целом неотъемлемой «нестроимостью» гитар ничего не поделаешь. Так что засада с главным рок-инструментом.
[Еще оффтопик] Набор композиций, которые будут упомянуты в этом, так сказать, «эссе», может показаться несколько диким. Однако критерии отбора были очень простыми:
- произведение должно начинаться с вступления «на одних аккордах» (без сложной мелодии)
- желательно, чтобы основным инструментом в аранжировке было фортепиано или, еще лучше, электронные клавиши. Если аранжировка гитарная, запись должна быть студийной (см. выше насчет особенностей этого замечательного инструмента)
То есть я пытался упростить себе жизнь, хотя бы в начале мучений с подбором каждой песни.
Но вернемся к нашим трем задачам.
Оставшаяся, третья, задача кажется тривиальной — отбираем три самых громких ноты и складываем из них аккорд. Но в реальности так ничего не получится (ну не совсем ничего — см. ниже, но толку от такого подхода очень мало). И вообще, эта задача оказалась самой сложной из всех.
Теперь обо всем по порядку.
Наивный метод определения аккордов
Сначала я сделал именно так, как написано выше — после анализа каждого «окошка» звукового файла отбирал три самых громких ноты и пытался слепить из них аккорд.
Первая композиция, на которой я пытался испытать магическое действие своей чудо-проги, была «Иуда будет в раю» Летова в варианте с Тюменского бутлега aka «Русское поле экспериментов (акустика)». Встуление к этой песне представляет собой долбеж на ми-минорном трезвучии в течение примерно десятка секунд.
Однако, прогнав по началу этой песни свою программу, я не обнаружил в выводе ни одного (!) аккорда Em. В основном не определялось ничего, изредка лезла всякая совсем «левая» чепуха. В чем дело, было непонятно. Пришлось реализовать почастотный дамп каждого окна в виде гистограммы из символов '*'. Из гистограммы первым делом выяснилось, что строй гитары отличается примерно на четверть тона от номинала. ОК, вводим поправку. Ура! Начали определяться ноты E и H — 1-я и 3-я в аккорде. А вот где G?
Дальнейшее исследование дампа показало следующее:
- спектр басовой «ми» размазан от D до F# с несколькими локальными максимумами, в итоге второй по громкости нотой иногда оказывается D#
- Откуда-то настойчиво лезет «ля» (может, это квинтовый унтертон от «ми»?). И когда D# куда-то пропадает, она занимает его место. В этом случае есть шанс получить в выводе Asus2, что то же самое, что Esus4, с точностью до выбора басовой ноты (в музыке это называется «обращение»). Уже что-то, но мне-то нужен Em!
- «Соль» в аккорде Em в его станадартной аппликатуре (в первой позиции) звучит только на одной струне — на третьей (для сравнения, «ми» — на трех). А еще в этой подпольной записи, видимо, из-за плохого качества оборудования, сильно порезана большая часть частот.
Видимо, поэтому G редко когда оказывается даже на 4-м месте
В общем, забил я на подбор Летова. И вообще, стало понятно, что нужно искать другой способ анализа хромограммы. Но, справедливости ради, надо сказать, что существует в природе как минимум один фрагмент, который нормально подбирается таким способом. Это вступление к песне Ольги Пулатовой «Розовый слон», представляющее собой арпеджио на электронных клавишах. Программа на нем выдала следующий результат (после ручной вычистки артефактов, образующихся «на стыках» аккордов и убирания подряд идущих повторов): Fm Cm (c db f) Ab Abm Eb Ebm B. ((c db f) — нестандартное созвучие, которое без особого ущерба может быть заменено на Db). Независимая проверка показывает, что аккорды правильные.
Вот она, сила тупой железки! Руками Олин изыск с тремя тональностями на 8 аккордов можно подбирать долго и безуспешно… Но, увы, повторюсь, это единственная известная мне композиция, которая успешно анализируется таким способом. Причины провала понятны — с одной стороны, мешают обертона и «левые» частоты гитарных «примочек», с другой — аккорды редко звучат сами по себе, поверх них с большей, причем, громкостью обычно идет мелодия — вокал, гитарное/клавишное соло и т.п. Мелодия редко когда полностью вписывается по нотам в гармонию — это слишком уныло, в итоге в потоке звука постоянно образуются «временные» созвучия, не соответствующие никаким каноническим аккордам, и все ломается.
Чуть менее наивный способ
Пришлось лезть в гугль и копать. Тема оказалась довольно популярной в научной и околонаучной среде, и в природе есть что по ней почитать, если не пугаться терминов типа hidden Markov model, naive bayesian classifier, gaussian mix, expectation maximization etc. Я поначалу боялся лезть во все эти дебри. Потом разобрался потихоньку.
Вот тут лежит статья, которая оказалась для меня наиболее полезной:
http://academia.edu/1026470/Enhancing_chord_classification_through_neighbourhood_histograms
Для начала авторы предлагают не искать точные совпадения с аккордами, а оценивать степень «близости» хромограммы к аккорду. Они предлагают три способа оценки такой близости:
- максимальное скалярное произведение хромограммы на шаблон аккорда
- наивный байесовский классификатор
- оценка параметров гауссовой смеси при помощи метода expectation maximization и использование расстояния Махаланобиса в качестве меры близости хромограмм
Третий способ после несколько более детального изучения по другим источникам я откинул – он, судя по выводам из вышеупомянутой статьи, дает результаты немногим лучше тривиального первого способа, а геморроя с матричной арифметикой, вычислением определителей и т.п. много.
А вот два первых я реализовал.
Первый способ суперпростой. Пусть у нас есть аккорд (для определенности Am) и хромограмма. Как определить, насколько хромограмма «похожа» на аккорд?
Берем маску нот, звучащих в аккорде — типа той, что мы рисовали для тональности. Для Am это будет 1 0 0 1 0 0 0 1 0 0 0 0. Умножаем эту маску скалярно на хромограмму, как будто это 12-мерные вектора (ну то есть тупо суммируем элементы хромограммы с теми индексами, по которым в маске стоит единичка). Вуаля – вот она, мера «похожести». Перебираем все аккорды, какие знаем, находим тот, у которого «похожесть» самая большая — считаем, что он и звучит.
Второй способ в реализации немногим сложнее, но требует обучающих данных. Основан он на теореме Байеса. «На пальцах» это выглядит так.
Есть понятие условной вероятности: условная вероятность P(A|B) — это вероятность события A при условии, что событие B наступило. Эта величина определяется вот таким тождеством: P(AB) == P(A|B) * P(B), гдеP(AB) — вероятность совместного наступления событий A и B.
Отсюда:
P(AB) == P(A|B) * P(B)
P(AB) == P(B|A) * P(A)
То есть, при условии ненулевой P(A)
P(B|A) == P(A|B) * P(B) / P(A)
Это и есть теорема Байеса
Как нам это использовать? Перепишем формулировку теоремы в удобных для нашей задачи обозначениях:
P(Chord|Chroma) = P(Chroma|Chord) * P(Chord) / P(Chroma),
где Chord — аккорд, Chroma — хромограмма
Если мы откуда-то узнаем распределение хромограмм в зависимости от аккорда, то можно найти наиболее правдоподобный аккорд для заданной хромограммы, путем максимизации произведения P(Chroma|Chord) * P(Chord) — поскольку хромограмма у нас задана, и P(Chroma), стало быть, константа.
Осталось понять, где взять распределения P(Chroma|Chord). Можно, например, дать программе «послушать» записи конкретных заведомо известных аккордов, чтобы она оценила на их основе эти распределения. Но тут есть нюанс. Вероятность получить конкретное значение хромограммы на «обучающем» примеры ничтожно мала — просто потому, что возможных значений очень-очень много. В итоге при использовании результатов обучения для реальной работы в подавляющем большинстве случаев P(Chroma|Chord) для всех значений Chord окажутся равными нулю, и максимизировать будет нечего.
Можно (и нужно) перед классификацией упростить хромограммы, например, поделив диапазон относительной амплитуды [0, 1], на котором определены компоненты хромограммы, скажем, на 3 части (со смыслом «почти так же громко, как самая громкая нота», «несколько тише, чем самая громкая нота», «совсем тихо по сравнению с самой громкой нотой»). Но все равно вариантов будет слишком много.
Следующее, что можно сделать — это предположить, что распределение вероятностей каждой компоненты хромограммы независимо от остальных компонент. В этом случае P(Chroma|Chord) = P(c1|Chord) *… * P(c12|Chord), где c1..c12 – компоненты.
хромограммы, и мы получаем для этого частного случая вот такую формулировку теоремы Байеса:
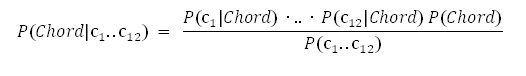
А вот P(ci|Chord) уже можно извлекать даже из скудного количества обучающих данных — если, конечно, «упростить» хромограмму, ограничив область определения ci тремя значениями, как мы договорились выше.
Осталось откуда-то взять P(Chord) для всех рассматриваемых аккордов. Не беда — для этого подойдет любой сборник песен с аккордами, главное, чтобы песен было много, и они были разных авторов.
Классификатор, основанный на максимизации выражения P(c1|Chord) *… * P(c12|Chord) * P(Chord) по параметру Chord, и называется наивным Байесовским классификатором. И в данном конкретном случае его «наивность» существенна, так как в реальности компоненты хромограммы являются зависимыми случайными величинами — например, из-за тех же обертонов. Тем не менее, как мы увидим дальше, этот подход работает.
Все это легко реализуется — код самого классификатора и «подсистемы» его обучения куда меньше, чем приведенное тут описание. Обучал я его на наборе мажорных и минорных рояльных аккордов с какого-то сайта бесплатных семплов и сборнике авторской песни 90-х годов с аккордами (первое, что нашлось в интернетах в виде единого текстового файла).
Теперь о результатах полевых испытаний. В испытаниях участвовали, помимо уже упомянутых My Friend Of Misery и «Розового слона», следующие композиции:
- Чиж&Co «Ассоль». Акустическая гитара, «хитрые» аккорды, первая половина песни в ре-миноре с не слишком сильными отсутплениями в некоторых местах
- Е.Летов «Солдатами не рождаются» в варианте с концертного сборника «Музыка весны». Акустическая гитара, на вид нормально настроенная… Аккорды — обычные трезвучия, маршеобразный «бой», все в одной тональности. Запись, хоть и концертная, хорошего качества
- О.Пулатова «Во сне» с «Домашних записей». Акустическое пианино, ужасное качество записи; начинается с обычных трезвучий, возможно, с измененным басом, затем начинаются мелодические украшательства. Выходы за тональность на слух есть, но не очень радикальные… Хотя и в «Слоне» на слух не очень радикальные...
Что получилось. Оба классификатора работают очень дергано, все время прыгая с аккорда на аккорд. Наивный Байес чуть постабильнее, чем максимум скалярного произведения, но, похоже, только потому, что «знает» меньше аккордов (только мажорные и минорные). Поскольку он, в отличие от «скалярного» собрата, «знает» вероятности, с которыми встречаются разные аккорды в авторской, блин, песне 90-х годов, то ведет он себя несколько быдловато, пытаясь, грубо говоря, везде засунуть «три блатных». Проблески разума встречаются у обоих классификаторов, но почему-то как правило на разных фрагментах одного и того же произведения. Лучше всех они справились с Misery. Байес периодически довольно стабильно выдавал паровозы Dm и Am, что правильно (там гармония типа Dsus2/E Am/E много-много раз; /E — это с басом «ми» в смысле). Знающий слишком много аккордов «скалярный» классификатор случайно блуждал между Dsus2, Asus2 (он же Dsus4), D, Dm, D5+ и левым мусором в попытках распознать Dm, аналогично вел себя и на Am.
Кое-что удалось вытянуть и из «Во сне». Несмотря на плохое качество звука, из горы мусора в выводе удалось вручную выделить почти правильные аккорды вступления Cm Eb Bm (на самом деле, последний аккорд B, как и положено в до-миноре) и куплета — Cm Gm Cm Gm Ab F Ab F. Вторая, «украшенная», часть вступления утонула в мусоре (забегая вперед — я ее так и не подобрал, более продвинутые методы классификации тоже выдают ерунду).
Из «Солдатами не рождаются» не удалось получить вообще ничего… Почему — не понимаю. В дампах спектра мусор. Но звучит-то на слух нормально и подобрать вручную вполне можно — Am C G H там во вступлении, правда, насчет тональности я не уверен — известный зверь на ухо наступил).
С «Ассолью» лучше справился наивный Байес. Ему явно понравилась КСП-шная гармонияв ре-миноре, и проблески разума у него случались довольно часто — процентов 20-25 аккордов он подобрал правильно, что на общем печальном фоне и с учетом «хитрых» аккордов тов. Чигракова недурно. Но вот зачем он позаменял почти все A на F# и F#m? Нонконформист, однако.
В общем, было понятно, что надо рыть дальше.
Мы в пролете, и нам нечего терять, кроме цепей. Но не своих, а Маркова
Почему вышеописанные методы так плохо работают? Если вы умеете на чем-то играть, представьте себе, что вам предлагают подобрать песню, проигрывая по отдельности фрагменты длиной в полсекунды, причем не по порядку, а вразнобой, чтобы вы не могли учитывать уже подобранную часть при работе с очередным «квантом». Получится у вас что-нибудь? Рискну предположить, что даже в случае наличия у вас абсолютного слуха результат будет плачевным.
Посему авторы упоминавшейся выше работы (равно как и других подобных исследований) предлагают после оценки «похожести» хромограммы на разные аккорды применять, как они выражаются, musical knowledge. У них это тайное знание сводится к тому, что вероятность встретить один из аккордов, который уже встречался ранее в композиции (вернее, в некотором ее временнОм окне) выше, чем такая вероятность для ранее не встречавшихся аккордов. При этом они учитывают «нечеткость» распознавания аккордов, частоту их встречаемости в анализируемом окне etc.
В целом, это эквивалентно такому эмпирическому знанию «Песни обычно пишутся в одной, максимум в двух тональностях, и поэтому набор используемых в них аккордов ограничен».
Я решил пойти немного другим путем. Исходил я из следующего:
- во-первых, надо учесть, что при небольшом размере анализируемого при помощи преобразования Фурье окна велика вероятность, что аккорд между двумя последовательно идущими окнами не меняется (несколько окон, идущих подряд, попадают в период звучания одного аккорда)
- во-вторых, вероятности переходов с одного аккорда на другой для каждой пары конкретных аккордов разные. На самом деле, конечно, вероятность встретить на очередном месте в последовательности конкретный аккорд зависит от более длинной «истории» (например, если мы колеблемся между G и Gm, то после Am Dm, скорее всего, будет G, а после B Dm — скорее Gm). Но такая модель показалась мне слишком сложной в реализации, и я решил ограничиться учетом только одного предыдущего аккорда.
С таким допущением для моделирования процесса смены аккордов можно воспользоваться цепями Маркова.
Представим себе систему с конечным (либо бесконечным, но счетным, т.е.«нумеруемым») множеством состояний S. Пусть она «живет» в дискретном времени, у которого есть начальный «0-й» момент и затем каждый момент времени можно обозначить его номером — t1, t2 и т.д. Пусть задано распределение вероятностей для начального состояния системы P0(Si) и вероятности переходов P(S(tn) = Si|S(tn-1) = Sj). Такой случайный процесс, когда вероятность перехода системы в конкретное состояние зависит только от ее текущего состояния, называется марковской цепью (в нашем случае — с дискретным временем). Если распределение вероятностей переходов не зависит от момента времени tn, марковская цепь называется однородной.
Я надергал распределения первого аккорда и переходов из кучи песен, распаковав 40-мегабайтный chm-ник с названием типа «весь русский рок с аккордами». Впрочем, авторы «гонят» — нет там аккордов даже для некоторых альбомов Кино и Крематория, не говоря уж о такой экзотике, как Пулатова (тексты, что интересно, есть). Но все же массив подборок довольно большой, так что можно считать выборку достаточно репрезентативной для оценки параметров нашей цепи Маркова. Анализ песен шел с 10 вечера до как минимум 5 утра следующего дня, правда, на «атомном» нетбуке.
Идем дальше. Помните теорему Байеса — P(Chord|Chroma) = P(Chroma|Chord) * P(Chord) / P(Chroma)? При помощи нашей марковской цепи мы будем оценивать P(Chord), а P(Chroma|Chord) пусть по-прежнему оценивается наивным байесовским и «скалярным» классификаторами. По поводу последнего — нам ведь, в общем-то, тут не нужна «настоящая» вероятность, поэтому можно считать наше скалярное произведение на хромограммы на маску аккорда «вероятностью» того, что эта хромограмма соответствует этому аккорду. Ну можно еще пронормировать эти скалярные произведения, чтобы их сумма по всем аккордам была равна 1, хотя для поиска максимума это не нужно, и я на это забил.
Итак, мы можем оценить P(Chord(t0) = Ci), исходя из статистической оценки распределения первых аккордов в сборнике русского рока (таким образом мы учитываем фактически разную частоту использования разных тональностей). Для следующих окон мы можем оценить P(Chord(tn) = Cn) как
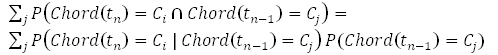
где P(Chord(tn-1) = Cj) были оценены на предыдущем шаге. Находим максимальное значение этого выражения для всех i и получаем наиболее вероятный аккорд. Обратите внимание – здесь учитывается тот факт, что мы не знаем достоверно, какой аккорд звучал в предыдущем окне, у нас есть лишь оценка распределения вероятностей различных аккордов.
Что же касается вероятности «неперехода» с аккорда на аккорд, то я добавил соответствующий параметр командной строки и подбираю оптимальное значение вручную. На самом деле эта вероятность зависит от соотношения между продолжительностями анализируемого окна потока и музыкального темпа произведения.
Вышеописанный алгоритм при правильном подборе параметров показал себя очень устойчивым. Сбиваясь с правильного пути при попытке «быдлофикации» какой-нибудь сложной гармонии, он честно пытается вернуться из расколбаса, и чаще всего у него это получается.
Пара небольших оптимизаций
Оптимизация №1. Было замечено, что у классификаторов «сносит крышу», как правило, на разных фрагментах. Также замечено, что, если классификатор несколько раз подряд определил один и тот же аккорд, то этот аккорд обычно правильный. Эти наблюдения привели к появлению следующей оптимизации: заводим кольцевой буфер на несколько аккордов и пихаем туда аккорды из вывода обоих классификаторов. Если в очередной раз классификаторы выдали разные аккорды для одного и того же окна, берем тот из них, который чаще встречается в буфере (ну а если одинаково часто встречаются или не встречаются вовсе — то первый из двух).
Оптимизация №2. Разные тональности используются в музыке (особенно в гитарной, где от них зависит аппликатура) с разной частотой. В основом народ, конечно, любит те, у которых поменьше значков альтерации в ключе — т.е. ля-минор/до-мажор, ми-минор/соль-мажор, ре-минор/фа-мажор, ну или на крайний случай си-минор/ре-мажор.
Из-за этого статистика по переходам между аккордами для наиболее распространенных тональностей оказывается «качественнее», чем для менее распространенных. Отсюда появилась возможность возможность «виртуального транспонирования» – ключи командной строки, который говорит программе «подбирай аккорды в той тональности, которую видишь, но вероятности переходов бери так, как будто все звучит на n полутонов ниже/выше».
Этот подход нередко используется при ручном подборе — например, мы знаем, что песня в до-миноре, но подбираем аккорды в ля-миноре, мыча мелодию на полтора тона ниже, потому что какие там аккорды в этом до-миноре — это еще сообразить надо, и еще пальцы все время держать барре устают.
Результаты этого этапа такие: при применении описанного выше подхода с обеими оптимизациями удалось подобрать аккорды к песням О. Пулатовой «Во сне» (кроме второй части вступления) и «Река времен» (вступление и куплет; тональность – некая помесь ля- и ми-минора) с достоверностью подбора около 70% или даже чуть больше. Ура!
Что касается второй половины вступления к «Во сне» — оптимальной реализацией, видимо, будет поехать в Одессу, случайно там встретить автора, спросить у нее аккорды, захардкодить.
Алгоритм Витерби
Алгоритм Витерби позволяет по косвенным данным (ну, то есть, в нашем случае — по хромограммам) за некоторый период жизни марковской цепи получить наиболее вероятную последовательность состояний (аккордов), пройденную процессом за этот период. Алгоритм очень простой, и я его пробовал реализовать, но, видать, я не умею его готовить. В зависимости от вероятности «неперехода» он либо залипает на одном аккорде, либо выдает кучу мусора (правда, обычно в правильной тональности). Может быть, это связано с требованием «результаты наблюдений должны 1-к-1 соответствовать пройденным «шагам» случайного процесса». Но, с другой стороны, кто мешает считать, что у нас «шаг» имеет фиксированное физическое время жизни, а потом наступает следующий шаг, даже если состояние не изменилось? Не знаю. А может, просто где-то есть ошибки в коде — отлаживать такие вещи нелегко…
Ну вот и всё. Спасибо за внимание!
Исходники можно взять тут: https://github.com/t0mm/ChordDetector
Автор: t0mm
