Приветствую, друзья.
Как вы знаете, в последнее время технология разработки игр для мобильных платформ развивается очень бурно. Игры пишутся на самых разных движках и языках, мы не будем в этой статье обсуждать, почему тот или иной язык/движок лучше или хуже (правда ведь?). Разработчики пытаются придумать новые интересные и удобные элементы управления игрой. Мне как игроку очень нравится использовать в игре геометрические элементы. Например такие, как в игре Джаггернаут для мобильных устройств.
Я попробую рассказать вам об алгоритме определения нарисованных 2d фигур. Свою версию движка я написал на языке ActionScript 3.0. При желании(и наличии базовых знаний по геометрии) его можно реализовать на любом другом.
Итак, нам необходимо по нарисованной руками фигуре определить процент схожести с имеющейся:
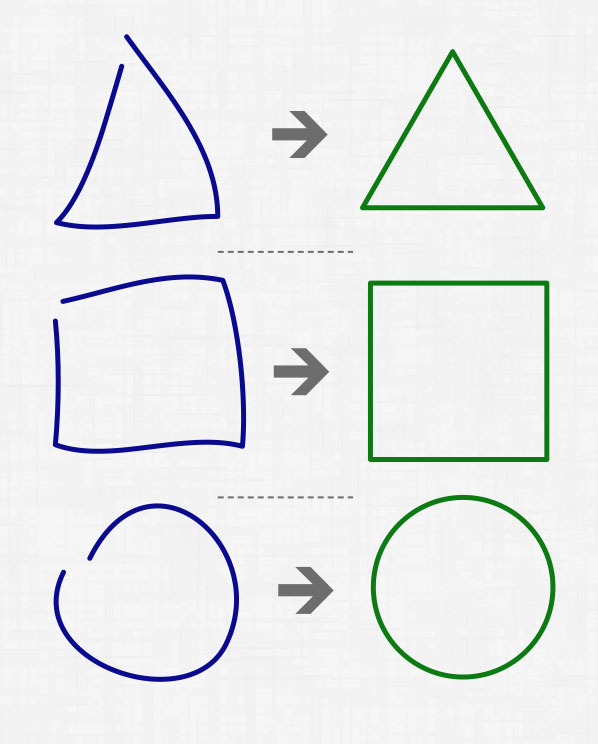
Базовая геометрия
Для реализации алгоритма нам понадобятся базовые формулы геометрии на плоскости.
[F1] Длина отрезка:
len = sqrt((x2-x1)^2 + (y2-y1)^2);
[F2] Векторы направления и нормали линии:
// координаты вектора направления линии
directX = x2-x1;
directY = y2-y1;
// координаты вектора нормали к линии
normaleX = -directY;
normaleY = directX;
[F3] Уравнение прямой на плоскости Ax+By+C=0
Получить коэффициенты A,B и C из уравнения прямой, зная две точки этой прямой, можно так:
A = -normaleX;
B = -normaleY;
C = -A*x1 - B*y1;
[F4] Положение точки относительно прямой.
Будем считать что точка лежит над прямой в том случае, если формула Ax+By+C при подстановке значений даст значение больше нуля. Если значение равно нулю, то точка принадлежит этой прямой. Представьте себе, что первая точка линии лежит в левой части экрана, а вторая в правой, так вот, все точки, которые лежат над этой линией(в верхней части экрана) дадут положительное значение при подстановке в уравнение прямой. Очень важно понять, где первая(начальная) точка, а где вторая(конечная): если у вас есть точки p={x,y} и q={x,y}, и вы рассчитываете направление(и вектор нормали) используя формулу:
directX = q.x-p.x;
directY = q.y-p.y;
, то первая(начальная) точка будет p, а вторая(конечная) — q.
[F5] Принадлежность точки отрезку
Точка o принадлежит отрезку p-q, если она лежит на прямой, проходящей через эти точки, и если она лежит между двумя заданными точками отрезка. Алгоритм принадлежности следующий:
— определяем, лежит ли точка на прямой ([F4])
— находим длины отрезков([F4]) o-p и o-q, если хоть одно из этих значений больше чем длина отрезка p-q, значит, точка o не лежит внутри отрезка p-q
[F6] Точка пересечения бесконечно длинных прямых
// прямые, заданные по двум точкам
l1 = {p1,p2};
l2 = {p1,p2};
//
d = (l2.p2.y-l2.p1.y)*(l1.p2.x-l1.p1._x) - (l2.p2.x-l2.p1.x)*(l1.p2.y-l1.p1.y);
a = (l2.p2.x-l2.p1.x)*(l1.p1.y-l2.p1._y) - (l2.p2.y-l2.p1.y)*(l1.p1.x-l2.p1.x)
// точка пересечения
x0 = l1.p1.x + a*(l1.p2.x-l1.p1.x)/d
y0 = l1.p1.y + a*(l1.p2.y-l1.p1.y)/d
Имейте ввиду что, если d=0, значит прямые параллельны.
[F7] Точка пересечения двух отрезков. Точка пересечения бесконечной линии и отрезка.
Если проверяется пересечение двух конечных отрезков или бесконечной линии и конечного отрезка, необходимо сперва определить точку пересечения двух бесконечных линии([F6]) и произвести проверку на принадлежность этой точки ко всем участвующим отрезкам ([F5]).
Треугольник — элементарный полигон как основа всего
Как вы знаете треугольник является самым простым полигоном. Многие расчеты полигонов связаны с треугольниками, поэтому приведу несколько формул для работы с ними.
[F8] Геометрический центр треугольника
Центр треугольника(или Центроид) — это среднее арифметическое координат точек треугольника. Определяется по формуле:
x0 = (a.x+b.x+c.x)/3;
y0 = (a.y+b.y+c.y)/3;
[F9] Площадь треугольника
Зная только координаты точек треугольника, определить его площадь можно, умножив длины двух сторон на синус угла между этими сторонами.
[F10] Полигон на плоскости
Полигон P на плоскости задается набором вершин: v1,v2,...,vn, где n — количество вершин. Полигон имеет ребра, которые образуются соединением соседних вершин: e1={v1,v2}, e2={v2,v3},...,en={vn,v1}.
[F11] Ограничивающий прямоугольник полигона
Ограничивающий прямоугольник задается объектом bounds={x,y,width,height}, где x и y — это минимальные координаты вершин полигона, а width и height — разница между максимальными и минимальными координатами вершин.
[F12] Центр полигона
Под центром обычно понимают разные сущности, например, центр системы точек или центр масс по площади… Мы будем использовать центр масс, который высчитывается по следующем алгоритму. Необходимо разбить полигон на треугольники, неважно какие, можно просто использовать вершины по порядку. Находим сумму произведений центров треугольников и их площадей и делим эту сумму на общую площадь полигона. Площадь полигона высчитывается как сумма площадей его треугольников.
// массив треугольников полигона
var triangles:Array = ... ;
// центр полигона
var centerX:Number = 0;
var centerY:Number = 0;
// площадь полигона
var polygonSquare:Number = 0;
//
for (i=0; i<triangles.length; i++) {
var triangle = triangles[i];
centerX += triangle.center.x*triangle.square;
centerY += triangle.center.y*triangle.square;
polygonSquare += triangle.square;
}
centerX /= polygonSquare;
centerY /= polygonSquare;
[F13] Положение точки относительно полигона
Точка находится внутри полигона в том случае, если эта точка находится «снизу» по отношению ко всем ребрам при обходе по часовой стрелке. Положение точки относительно линии можно определить по формуле F4. Если точка лежит «сверху» относительно всех ребер, значит, она лежит вне полигона
[F14] Пересечение бесконечной линии и полигона
Для определения точек пересечения линии l с полигоном P необходимо найти все точки пересечения прямой l со всеми отрезками e1,e2..., используя формулу [F7].
Определение схожести фигур
Итак, что у нас имеется на входе? У нас есть исходный рисунок — полигон template, заданный набором вершин v1,v2,...,vn, и есть полигон draw, состоящий из набора точек, которые мы получили в процессе рисования. Прежде чем начать их сравнивать, полигон draw необходимо «привести» к полигону template. Т.е. необходимо применить трансформацию сжатия(scale) и смещения(translate) так, что бы центры полигонов совпадали и полигон draw имел с template максимально похожие размеры ограничивающего прямоугольника(bounds.width и bounds.height):
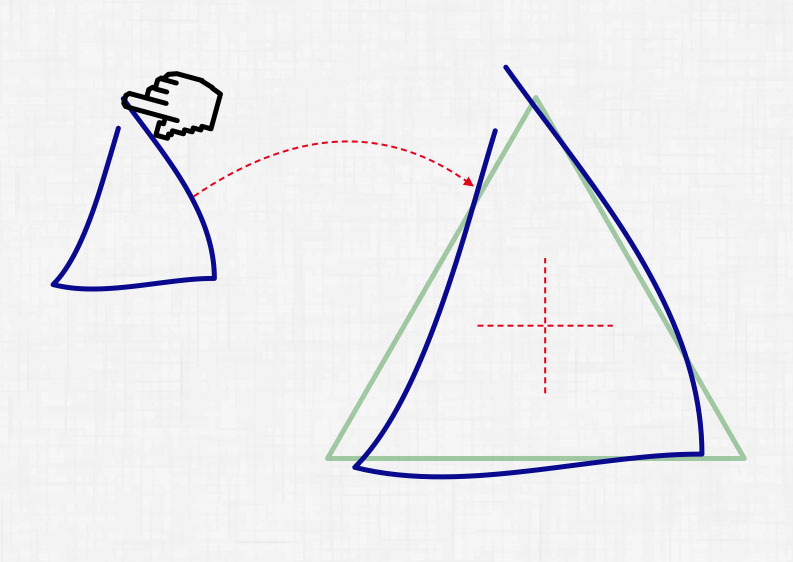
Алгоритм приведения полигонов:
// исходный шаблон
var template = ... ;
// нарисованный полигон
var draw = ... ;
// сжатие по ширине
var scaleW:Number = template.bounds.width/draw.bounds.width;
// сжатие по высоте
var scaleH:Number = template.bounds.height/draw.bounds.height;
// среднее значение сжатия
var scale:Number = (scaleW+scaleH)/2;
// применяем трансформацию сжатия
draw.matrixScale(scale);
//
// смещение по X
var dx:Number = draw.centerWeight.x-template.centerWeight.x;
// смещение по Y
var dy:Number = draw.centerWeight.y-template.centerWeight.y;
// применяем трансформацию смещения
draw.matrixTranslate(dx, dy);
Имейте ввиду что centerWeight — это центр масс полигона.
Определить схожесть фигур можно двумя алгоритмами, назовем их Радиальный и Габаритный. Давайте разберем их.
Радиальный алгоритм
После того как вы подогнали нарисованный полигон к шаблону, мы можем начать их сравнивать. Суть радиального метода состоит в следующем. Выпускаем из центра луч и находим точки пересечения этого луча с полигонами. Находим расстояние между точками пересечения и запоминаем его. Далее рисуем новый луч с определенным шагом угла, и так же находим расстояние между точками пересечения. Сложив в конце полученные расстояния между точками пересечения, мы получим некоторое значение. Чем меньше это значение, тем ближе нарисованная фигура к шаблону. Пример можно посмотреть на изображении:
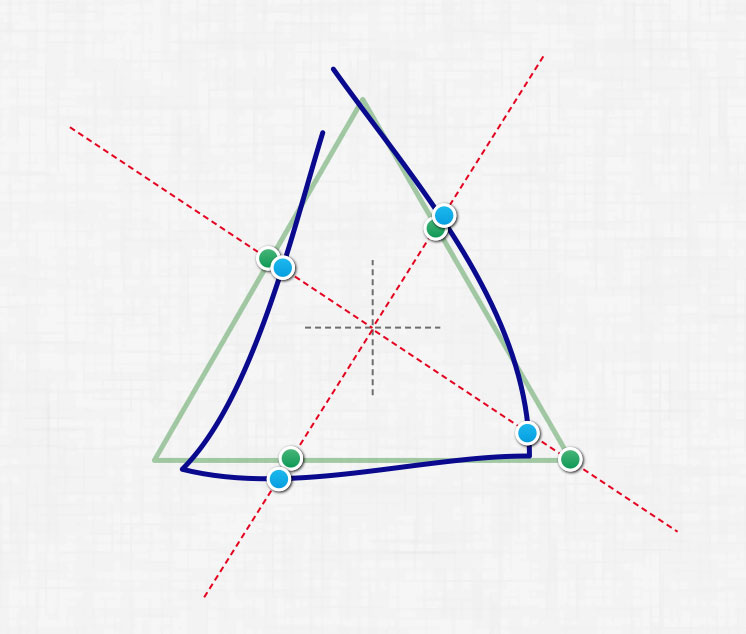
Чем больше лучей будут выпущены, тем точнее будет проверка. Также можно задать погрешность, например, на сколько средняя длина между точками пересечения луча с полигонами отличается от ширины/высоты(или среднего арифметического ширины и высоты) ограничивающего прямоугольника полигона-шаблона. Проверить работу алгоритм можно во флешке
Габаритный алгоритм
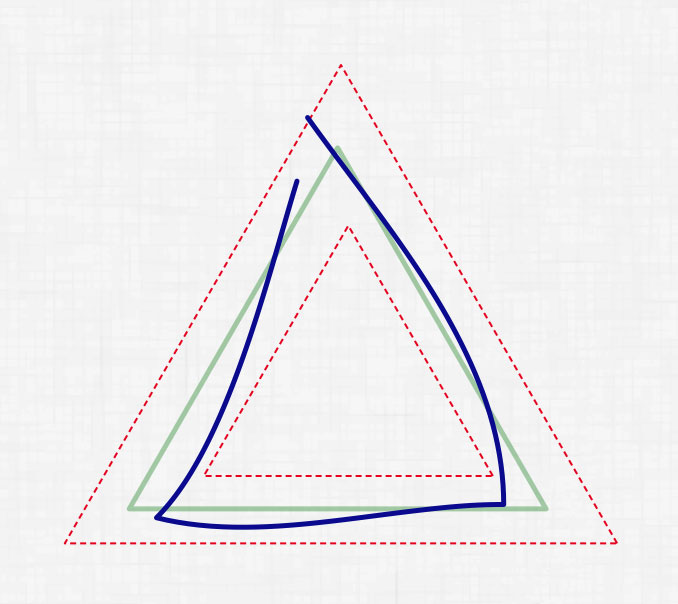
Габаритный алгоритм заключается в том, что бы задать два ограничивающих полигона, внутри которого должны располагаться все точки рисуемого полигона. Т.е. необходимо создать два клона шаблона и применить к ним трансформацию сжатия: к одному в меньшую сторону, к другому — в большую. Далее проверяем все точки, которые находятся внутри большого полигона и за пределами маленького, после чего можем определить процент не попавших в эту область точек. Пороговое значение процента может быть уровнем точности нарисованной фигуры.
Ссылки
Библиотеки используемые для реализации на языке ActionScript: FPGeometry2d.swc и FPGeomControl.swc.
Автор: FlashPress

