Моделирование гидродинамики: Lattice Boltzmann Method

Моделирование извержения вулкана
с помощью Lattice Boltzmann Method. (с) Источник

В этой статье я расскажу о численном методе моделирования гидродинамики Lattice Boltzmann Method, LBM. Он превосходит другие известные методы (например, finite element method) в легкости распараллеливания, возможности моделирования многофазных потоков, моделировании потоков в пористых средах. Кроме того, вычислительный алгоритм содержит только простейшие арифметические операции. Метод весьма новый, первые коммерческие продукты на его основе стали появляться около 2010 года.

На хабре уже была серия статей по физике жидкости, и эта статья может быть ее логическим продолжением. Она написана с таким расчетом, чтоб как быть полезной людям, хорошо знающим гидродинамику и методы моделирования, так и понятной новичкам в этой области (например, с людям с образованием software engineer). Конечно, в связи с этим многие вещи будут излишне подробными для экспертов, а на некоторые не хватит места. Статья получилось достаточно большой, но мне не хотелось бы разбивать ее на несколько частей.

Зачем все это нужно? Точнее, в каких отраслях нужно моделировать гидродинамику:

• самолетостроение, ракетостроение, автомобилестроение (характеристики кузова, работа двигателя, сопла)
• промышленная химия (разделение веществ, химические реакторы)
• метеорология, геология (потоки жидкости сквозь пористые среды, песчаники, дамбы)
• другие инженерные отрасли (ветряные электростанции)
• медицина (потоки крови, лимфы)

Статья будет включать следующие разделы:

• Обзор физики — высокоуровневый обзор основных необходимых уравнений
• Основная идея—описание основного принципа алгоритма
• Технические детали—более подробное объяснение исходных уравнений, вывод вычислительной схемы
  • Уравнение Навье-Стокса
  • Уравнение Больцмана
  • Дискретное уравнение Больцмана
  • Иллюстрация вычислительной схемы
  • Пространственные решетки
  • Равновесные функции распределения
  • Несжимаемость
  • Вязкость и число Рейнольдса
  • Еще раз, все вместе

• Разное
  • Дополнения к алгоритму
  • Подводные камни
  • Существующие решения
  • Что почитать

Обзор физики

Гидро- и аэродинамика макроскопически описывается уравнением Навье-Стокса. Оно показывает, каким будет давление, плотность и скорость жидкости в каждой точке пространства в каждый момент времени—в зависимости от начальных и граничных условий и параметров среды.

С другой стороны, для разреженных газов справедливо уравнение Больцмана, которое описывает, как меняется плотность распределения частиц по скоростям в каждой точке пространства со временем. Если проинтегрировать распределение частиц по скоростям в данной точке, можно получить плотность и макроскопическую скорость в данной точке. Другими словами, макроскопически уравнение Больцмана эквивалентно уравнению Навье-Стокса.

Основная идея

Несмотря на то, что для плотных жидкостей уравнение Больцмана не применимо, если мы научимся его моделировать, то сможем моделировать и уравнение Навье-Стокса для этих жидкостей. То есть мы тем самым заменяем нижележащий уровень абстракций (микроскопическое уравнение для плотных жидкостей) физически неправильной реализацией (микроскопическое уравнение для разреженных газов), но так, что верхний уровень (макроскопическое уравнение Навье-Стокса) описывается верно.

Ситуация иллюстрируется картинкой ниже.

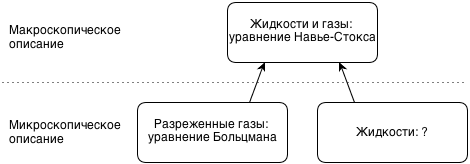
Вопросительный знак в ней символизирует тот факт, что я не знаю, какое уравненине описывает поведение плотных жидкостей на микроскопическом уровне. Иногда вместо «микроскопический» говорят «мезоскопический»—в том смысле, что микроскопическое описание—это описание поведения отдельных атомов и молекул, а уравнение Больцмана описывает потоки молекул.

Поскольку компьютер не умеет работать с непрерывными величинами, нам необходимо дискретизировать уравнение Больцмана: по времени, по пространственным координатам (получаем пространственные узлы для моделирования) и по возможным направлениям частиц в каждом пространственном узле. Направления выбираются специальным образом, и всегда указывают в некоторые соседние узлы.

Технические детали

В этом большом разделе находится более подробное объяснение исходных уравнений и вывод вычислительной схемы. Действительно важные уравнения должны быть понятны всем читателям с техническим образованием (требуются основы линейной алгебры, интегрального исчисления). Те уравнения, что непонятны, скорее всего, не важны (это те, где есть набла). Векторы обозначаются жирным шрифтом.

Уравнение Навье-Стокса

Вариант уравнения для макроскопической динамики несжимаемых жидкостей и газов выглядит так:
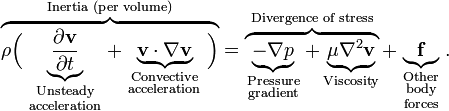          (1)

здесь v – скорость потока, ρ – плотность жидкости, p – давление в жидкости, f – внешние силы (например, гравитация).

Если вы не знаете, что такое перевернутые треугольнички и частные производные—не переживайте, они нам в дальнейшем не понадобятся, а вычислительный алгоритм содержит только простейшие арифметические операции.

Подробный вывод и физический смысл можно изучить на википедии и хабре, я же здесь приведу основную идею.

Мысленно выделим в жидкости некий малый объем и проследим за его движением. Ускорение, действующее на данный объем жидкости, определяется (i) давлениями слева, справа, сверху, снизу и т.п. (притом они частично компенсируют друг друга), (ii) действием внутренних сил трения в жидкости (iii) внешними силами. С другой стороны, ускорение можно выразить через разницу скоростей в начальный момент времени в начальной точке и в некоторый следующий момент времени в той новой точке, где будет находиться объем жидкости.

Если теперь подставить эти величины в уравнение Ньютона F = ma, после несложных преобразований мы получим уравнение выше. Слева находится ma, справа—F.

Уравнение Больцмана

Это уравнение оперирует функцией распределения плотности вероятности частиц по координатам и по скоростям, f(r, v,t). Величина f(x, y, z, v_x, v_y, v_z, t) dx dy dz dv_x dv_y dv_z показывает, какая доля частиц в момент времени t находится в кубе от x до x+dx, от y до y + dy, от z до z + dz со скоростями в диапазоне от v_x до v_x + dv_x, от v_y до v_y + dv_y, от v_z до v_z + dv_z. Ее также можно записать в виде .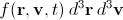

Эта функция обычно нормируется на массу газа в исследуемой системе, поэтому макроскопическая плотность газа в каждой точке определяется как сумма (интеграл) от плотности вероятности в данной точке по всем возможным значениям скорости,
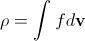.          (2)
Аналогично, макроскопическую скорость можно определить через
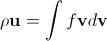.          (3)

Основная идея для вывода уравнения похожа на вывод уравнения Навье-Стокса. Давайте мысленно выделим в данный момент времени в данном небольшом объеме пучок молекул, летящих в данном направлении (точнее, узком конусе направлений). Через небольшой промежуток времени dt они окажутся в соседней точке (благодаря наличию скорости), их скорость сама по себе изменится из-за ускорения молекул внешними силами. Кроме того, на этом отрезке пути некоторые молекулы столкнутся с другими, изменят свою скорость, и мы больше не сможем включать их в исходный пучок. С другой стороны, в результате столкновений молекул в том же объеме, летящих в другую сторону, некоторые из них приобретут нужное направление скорости, и мы добавим их в пучок.

Это можно записать в следующем виде:
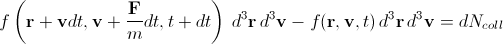,          (4)
где F—внешняя сила, m—масса молекулы, dN_coll—изменение числа частиц в пучке за счет столкновений.

Как определяется в общем виде величина dN_coll, от читателя останется скрытым. Нам понадобится только ее стандартное приближение—Батнагара-Гросса-Крука (BGK). В этом приближении dN_coll равно
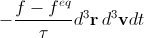,          (5)
где f^eq—равновесная функция распределения, распределение Максвелла-Больцмана, а τ – так называемое время релаксации.

В итоге получаем
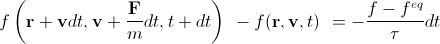.          (6)
Заметим, что f^eq зависит от макроскопических плотности и скорости в данной точке (то есть неявно от координаты и времени). Именно это уравнение нам понадобится в дальнейшем, но обычно его делят на dt и приводят к виду
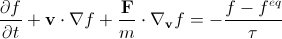,          (7)
где набла с индексом v – это набла по переменным скорости.

Дискретное уравнение Больцмана

Чтоб получить возможность моделировать динамику непрерывного уравнения Больцмана на компьютере, нам необходимо его дискретизировать. Для этого сначала введем равномерную сетку пространственных координатам—шаг сетки пусть будет одинаковым по всем осям. Поведение жидкости мы будем определять именно в узлах сетки. Фактически, мы разрешаем молекулам находиться только в определенных пространственных узлах. Кроме того, мы должны дискретизировать время—мы будем определять состояние жидкости в равноотстоящие друг от друга моменты времени. Кроме того, мы позволим молекулам иметь только определенные значения скорости—такие, чтоб за шаг по времени они успевали перейти в какой-нибудь соседний узел. Эти разрешенные направления будут одинаковыми для всех пространственных узлов. Очевидно, что по диагональным направлениям скорости частиц будут больше, чем по недиагональным.

Интуитивно можно заключить, что при бесконечно малом шаге времени и шаге пространственной решетки эта дискретная система перейдет в обычное уравнение Больцмана, которое, в свою очередь, переходит к уравнению Навье-Стокса в макроскопическом пределе. Как ни странно, это не такой простой вопрос, и мы его пока отложим.

В дальнейшем изложении везде предполагается, что система единиц такова, что шаг решетки является единицей длины, а шаг по времени—единицей времени.

Для простоты ниже будем предполагать, что внешние силы отсутствуют. Мы пронумеруем разрешенные направления скорости от 1 до Q с индексом i. Если теперь массу частиц, пролетающих из данного узла в направлении i за шаг времени обозначить как f_i, то уравнение (6) перейдет в
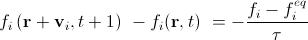.          (8)
Здесь мы учли, что шаг по времени равен единице, и заменили все dt из (6) на единицу. f_i^eq обозначает дискретную равновесную плотность распределения, зависящую от макроскопических массы и скорости в данном узле. Мы не указали, из какого именно узла будем использовать f_i^eq —из r + v_i t в момент времени t + 1 или из r в момент времени t. Для вычислительной схемы удобнее оказывается использовать узел r + v_i t в момент времени t + 1. Тогда уравнение выше можно разложить на две составляющие, распространение (streaming step) и столкновение (collision step).

Streaming step:
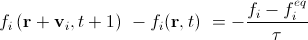.          (9)
Collision step:
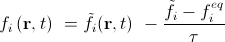.          (10)

Здесь f_i с тильдой обозначает массу частиц, пришедших в узел по направлению i, но еще не столкнувшихся с остальными пришедшими частицами. Streaming step иногда называют advection step.

Для дискретизированных направлений скорости масса и макроскопическая скорость в каждом узле будут рассчитываться как
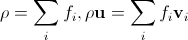.          (11)

Здесь и далее мы пишем везде плотность вместо массы, поскольку при единичном пространственном шаге решетки на каждый узел приходится единичный объем, и масса и плотность совпадут по значению.

Мы покажем, что равновесные функции распределения зависят от массы в узлах и макроскопической скорости. Поэтому после streaming step необходимо пересчитать массы и скорости в каждом узле, пересчитать равновесные функции распределения, и потом совершать collision.

Таким образом, на каждом шаге вычислительной схемы необходимо «распространить» частицы, то есть переместить частицы, летевшие из узла r в направлении i в узел r + v_i (проделать это для всех частиц и направлений). После этого необходимо пересчитать массы, скорости, равновесные функции распределения. Наконец, необходимо «столкнуть» частицы, прилетевшие в данный узел—то есть перераспределить частицы по направлениям.

Иллюстрация вычислительной схемы

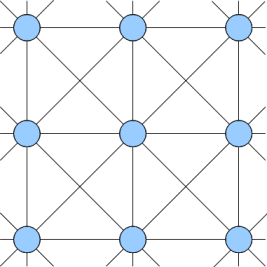
Проиллюстрируем вычислительную схему на примере двухмерной системы. Дискретизация на пространственные узлы и связи между ними (то есть разрешенные направления скорости) изображены на рисунке ниже. Пространственные узлы обозначены кружочками, связи между ними—тонкими линиями.

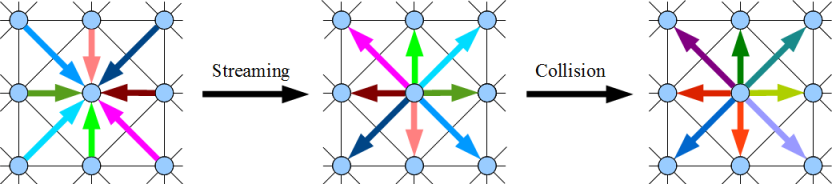
На следующем рисунке изображена одна итерация пары «streaming/collision». Цветные стрелки изображают потоки летящих молекул. Интенсивность цвета кодирует массу молекул, летящих в данном потоке, длина стрелок примерно соответствует пути, проходимом потоком за шаг по времени (лишь примерно, поскольку стрелки должны идти от центра узла до центра узла).

Пространственные решетки

В LBM под решеткой (lattice) понимается набор разрешенных векторов скорости (одинаковый для каждого пространственного узла). Это согласуется со стандартным математическим определением о решетке как о сущности, с помощью которой путем параллельных переносов можно получить все пространственную сетку (grid).

В LBM любая решетка должна содержать нулевой вектор из узла в себя самого—он описывает частицы, которые никуда не летят из данного узла. В LBM решетки обычно обозначаются аббревиатурой DnQm, где n—размерность пространства, m—число векторов в решетке. Например, D2Q9, D3Q19 и т.п.

В двумерном пространстве LBM решетка может состоять, например, из 5 векторов (2 вертикальных, 2 горизонтальных и нулевой вектор из узла в себя самого), а может из 9 векторов, как на иллюстрации выше (2 вертикальных, 2 горизонтальных, 4 диагональных, один нулевой). Это решетки D2Q5 и D2Q9, соответственно.

Очевидными факторами для выбора решеток являются: 1. точность моделирования (интуитивно понятно, что чем больше векторов в решетке, тем точнее моделирование) 2. вычислительные затраты (расчет на решетке D2Q5 будет быстрее расчета на D2Q9). Как ни странно, это не самые важные факторы. Самые важные факторы—это воспроизводимость уравнений Навье-Стокса и симметрия некоторых тензоров, построенных на векторах решетки.

Обычно используются решетки D2Q9, D3Q15, D3Q19. Решетки D2Q9 и D3Q19 изображены ниже. Базисные вектора решетки обычно обозначаются как e_i или c_i (они совпадут со скоростями v_i, введенными ранее при единичном шаге по времени). Ниже мы будем использовать обозначение e_i.

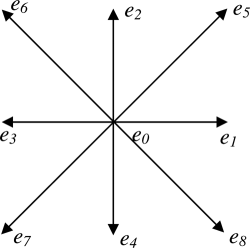
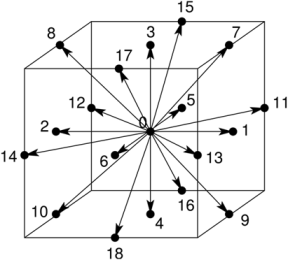
Выпишем базисные вектора для D2Q9:
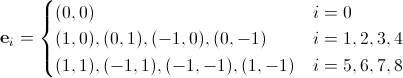          (11)

и для D3Q19:
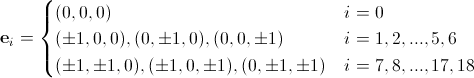          (12)

Еще раз напомню, что мы везде предполагаем, что шаг по времени равен единице, поэтому v_i = e_i.

Равновесные функции распределения

В непрерывном случае равновесная функция распределения (распределение Максвелла-Больцмана) равна
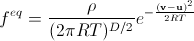.          (13)

Здесь есть ранее не встречавшиеся величины: R—универсальная газовая постоянная, T—температура, D—размерность пространства, v—вектор скорости, плотность вероятности для которого мы и находим. Здесь молярная масса газа принимается равной единице (она для нас не важна—важна только макроскопическая плотность). Можно считать это изменением единицы массы в нашем моделировании. Кроме того, функция нормируется на локальную макроскопическую плотность, а не на единицу. Заметим также, что обычно от v не отнимают макроскопическую скорость газа u. Это происходит потому, что обычно распределение исследуют в случае неподвижного газа, нам же необходимо перейти в локальную инерционную систему отсчета, движущуюся с текущей скоростью газа в данной точке в данный момент времени, чтоб использовать распределение Максвелла-Больцмана. Вычитание u и является таким переходом.

Предположим, что в данной точке пространства распределение молекул по скорости оказалось равновесным. Это распределение зависит от макроскопической массы ρ и скорости u. С другой стороны, мы можем вычислить ρ и u по функции распределения (см. формулы (2) и (3)). Очевидно, это вычисление должно дать правильные ρ и u (то есть это в каком-то смысле дополнительное ограничение на функцию распределения):
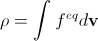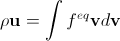, .          (14)

Такое же требование мы налагаем на вычисление плотности и скорости в дискретном случае:
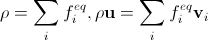.          (15)

Основным требованием для дискретных равновесных функций распределения является воспроизводство уравнения Навье-Стокса в пределе бесконечно малых шага по времени и шага решетки. Это эквивалентно тому, что если при заданных ρ и u мы попытаемся их снова рассчитать по равновесным функциям распределения в непрерывном и дискретном случае, результаты совпадут (см. замечание выше о том, что в дискретном случае вместо плотности имеется в виду масса), т.е.
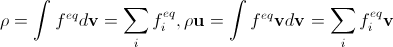.          (16)

Для однозначного определения равновесной дискретной функции распределения нам необходимо будет также включить аналогичное требование равенства макроскопических тепловых энергий в данной точке, мы его опустим для краткости.

Если просуммировать по направлениям скорости уравнение (10) для collision step, то с учетом формулы (16) можно показать, что collision step не изменяет макроскопические массы и скорости молекул, находящихся в узле.

Оказывается, если просто подставить дискретные векторы скорости e_i=v_i из (11) и (12) в непрерывную равновесную функцию распределения (13), равенства (16) не будут выполняться.

Оказывается также, что мы можем заставить равенства (16) выполняться, если разложим распределение Максвелла-Больцмана (13) в ряд Тейлора до второго порядка макроскопической скорости. Это соответствует тому, что величина u/sqrt(RT) очень мала. Это ограничение всегда должно выполняться в процессе моделирования во всех узлах.

Но даже разложения в ряд Тейлора недостаточно. Мы также должны ввести в дискретизированные функции f_i^eq специально подобранные множители w_i (детали вычислений можно найти в этой прекрасной статье—есть и бесплатная версия; конечно же, все окажется немного сложнее, чем в нашем поверхностном описании—на самом деле, расчет происходит через тензоры, вплоть до четвертого ранга, построенные на векторах решетки). Окончательно получим
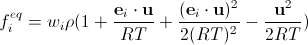.          (17)

Здесь кроется подвох: мы везде предполагаем, что шаг решетки и времени являются единицами длины и времени, соответственно. Потому мы не можем взять значение R из СИ, а температура здесь не равна температуре моделируемой жидкости в Кельвинах.

Чтоб определить их значения, заметим следующее. Предположим, что в жидкости имеется возмущение—то есть в некоторых узлах есть избыточная масса. Эта масса начнет «растекаться» по пространству, притом в крайнем правом узле в области возмущения она будет двигаться в том числе и по направлению (1, 0, 0) в 3D или (1, 0) в 2D. За единицу времени молекулы вдоль этих направлений пройдут единицу длины, то есть их скорость будет равна единице. Это означает, что скорость звука как скорость распространения возмущений в нашей системе тоже равна единице. С другой стороны, скорость звука равна sqrt(γ R T / μ), где γ—это постоянная адиабаты, μ—молярная масса, которую мы приняли равной единице ранее. Постоянная адиабаты γ равна 1 + 2 / d, где d—число степеней свободы молекул. В идеальном газе оно равно размерности пространства. В нашем газе молекулы могут двигаться только вдоль прямых, соединяющих узлы, потому размерность равна не трем (или двум), а единице. То есть γ=3, а sqrt(3 R T) = 1.

Обычно в литературе по LBM под «скоростью звука» понимают величину
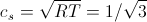.          (18)

Теперь, окончательно,
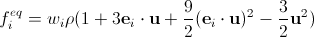.          (19)

Выпишем значения коэффициентов w_i для самых распространенных решеток.
Для D2Q9:
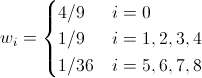          (20)

Для D3Q19:
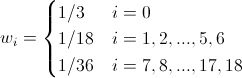          (21)

Несжимаемость

Ограничение на малую макроскопическую скорость жидкости теперь можно записать как
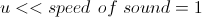.          (22)

Напомним, что число Маха есть отношение характеристической скорости газа в системе к скорости звука. Тогда ограничение выше соответствует малым числам Маха или несжимаемой жидкости. Действительно, если скорость звука (скорость распространения возмущений плотности) велика, то любое возмущение плотности быстро распространится на всю систему, и плотность станет снова одинаковой. То есть сжать жидкость в какой-либо одной локальной области вам не удастся.

Хорошее максимальное значение для макроскопической скорости в узлах будет, например, 0.01.

Вязкость и число Рейнольдса

Кинематическая вязкость ν в LBM (как обычно, в единицах решетки) рассчитывается как
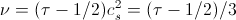.          (23)
Здесь τ—время релаксации, введенное ранее в формуле (5), c_s=1/sqrt(3)— «скорость звука», введенная в (18).

При моделировании гидродинамики без учета изменений температуры любая система с наперед заданной геометрией (например, труба с квадратным сечением) полностью описывается только одним безразмерным параметром—числом Рейнольдса, равным
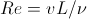,          (24)
где v—характеристическая скорость в системе (например, скорость в центре трубы), L—характеристическая длина в системе (например, длина стороны квадрата сечения).

Для стандартных геометрий обычно известна связь между характеристической скоростью и внешней силой (которая обеспечивает поток). Поэтому для моделирования с заданным числом Рейнольдса необходимо

1. выбрать характеристическую скорость v. Как мы выяснили, она должна быть намного меньше скорости звука. Например, 0.01.
2. рассчитать необходимую внешнюю силу для такой скорости
3. рассчитать вязкость по (23) так, чтоб получить нужное число Рейнольдса
4. рассчитать время релаксации по (24) так, чтоб получить нужную вязкость

Если задача моделирования составлена в единицах СИ (мол, сторона квадрата сечения трубы 1м, давление на входе трубы X Паскалей, на выходе—Y Паскалей), то сначала надо найти безразмерное число Рейнольдса, и воспользоваться алгоритмом выше.

Еще раз, все вместе

Перед моделированием надо задать начальные макроскопические массы и скорости в каждом узле. Потом задать потоки масс в каждом разрешенном направлении e_i в каждом узле (см. Подводные камни). Самый простой способ—указать потоки из равновесного распределения.

Для моделирования в цикле совершать

1. streaming step по формуле (9)
2. пересчет макроскопических масс и скоростей в каждом узле по формулам (11), пересчет равновесных потоков по всем направлениям по формуле (19)
3. collision step по формуле (10)

Моделирование обычно происходит до тех пора, пока система не находится в стационарном состоянии. Стационарность можно проверять, например, через разницу макроскопических скоростей и масс в каждом узле между соседними шагами, максимальную среди всех узлов.

Разное

Дополнения к алгоритму

Мы не коснулись включения внешних сил в моделирование (например, гравитации). Они приведут к небольшой добавке в уравнение (9) для streaming step.

Мы также не коснулись граничных условий—на поверхности тел и на входе и выходе системы (например, если на входе трубы задано постоянное давление или поле скоростей). В LBM есть большая свобода в моделировании таких условий, поскольку метод формулируется на микроскопическом уровне (потоки молекул), а такие граничные условия—на макроскопической уровне. Существует множество способов задать граничные условия на микроскопическом уровне—и множество алгоритмов.

Граничные условия на границе твердых тел в гидродинамике обычно выбираются как no-slip boundary conditions (то есть когда скорость жидкости на поверхности тел равна нулю). Обычно они реализуются через bounce-back conditions (когда потоки молекул отражаются в обратном направлении при пересечении твердой стенки).Об этом можно почитать здесь, раздел 4.6.

Модель столкновений, которую мы представили, называется single relaxation time. Существуют более совершенные модели, например, multiple relaxation time (в частности, double relaxation time).

LBM также поддерживает многофазность (моделирование потока смеси жидкостей или газов с разными параметрами).

Наличие теплопроводности (то есть переноса тепла в системе, изменения температуры в разных точках системы и, как следствие, изменения параметров системы—например, плотности) также поддерживается LBM. Температура моделируется как отдельный «газ», тоже по алгоритму LBM, но скорость этого газа определяется скоростью основной жидкости. Говорят, что температура в этом смысле является passive scalar. Есть немало статей по моделированию через LBM явления Rayleigh–Benard convection.

Мы совершенно не коснулись вопросов эффективной реализации и параллелизации.

Подводные камни

Если вы моделируете систему с теплопроводностью, то она будет описываться двумя безразмерными величинами. В случае Rayleigh-Benard convection обычно выбирают число Прандтля и число Рэлея. Для того, чтобы воспроизвести эту систему в единицах решетки, недостаточно просто воспроизвести обе этих безразмерных величины, правильно задав внутренние параметры системы (характеристическая скорость, внешняя сила, теплопроводность). Дело в том, что между внутренними параметрами будут существовать скрытые зависимости. Подробнее можно почитать тут.

Как мы уже сказали, при выборе характеристической скорости в системе не забывайте о том, что число Маха должно быть много меньше единицы (формула (22)).

LBM может стать нестабильным в некоторых системах при высоких числах Рейнольдса (когда поток, тем не менее, все еще ламинарный).

В LBM не выполняется галилеевская инвариантность. Впрочем, обычно это неважно.

В начале моделирования необходимо задать потоки молекул из каждого узла по всем разрешенным направлениям. Часто выбирают равновесное распределение потоков (формула (19)). Важно помнить, что равновесность не предполагает стационарность. То есть стационарные распределения при наличии градиентов скорости, внешней силы и т.п. отличаются от равновесных. Их расчет приведен здесь (формулы 12, 19, 20 по ссылке).

Существующие решения

Есть большой и очень зрелый open-source проект, целиком посвященный LBM—Palabos (PArallel LAttice BOLtzmann). У проекта есть и вики. Разработчики предоставляют платную консультацию по моделированию гидродинамики.

Здесь есть прекрасные обучающие примеры моделирования типичных систем на MATLAB. Например, Rayleigh–Benard convection (в наличии внешняя сила, теплопроводность, граничные условия, правильный перевод величин). Всего 160 строчек в MATLAB.

Есть множество коммерческих решений, например, это или это.

Подробный список коммерческих и некоммерческих пакетов по LBM можно найти на википедии.

Что почитать

Помимо всех ссылок, что есть в статье, можно порекомендовать эти списки статей и книг. В основном аналогичный список книг есть и на википедии.

На этом все,

Спасибо за внимание!

Автор: Bas1l

Источник