Итак, вы всё ещё не понимаете Хиндли-Милнера? Часть 2

В части 1 мы говорили о том, какие строительные блоки нужны для формализации Хиндли-Милнера, а в этом посте мы конкретизируем их определения и сформулируем формализацию в целом:

Формализация концепции выражения

Мы дадим рекурсивное определение того, что такое выражение; другими словами, мы определим большую часть типов выражений, расскажем, как создавать новые, более сложные выражения, исходя из существующих, и покажем, что создавать таким способом можно только допустимые выражения.

1. Переменные — допустимые выражения.
2. Если e — произвольное выражение, а x — произвольная переменная, то λx.e является выражением. Здесь поможет думать о e, как об обычном (но не обязательно) сложном выражении, включающем в себя x, т.е. x²+2, а затем о λx.e как об анонимной функции, которая принимает на вход x и возвращает результат вычисления выражения e для заданного значения x. Проще говоря, думайте об этом как о

   function(x) { return x^2 + 2; }
   

3. если f и e — допустимые выражения, то f(e) также является допустимым. Оно называется «наложением» (Application) по очевидным причинам.
4. Если x — переменная, а e₁ и e₀ — допустимые выражения, то замена каждого вхождения x в e₀ на e₁ также даст допустимое выражение. Т.е., если, например, e₁ = x²+2 и e₀ = y/3, то полагая x = e₀ в e₁, мы получим выражение (y/3)²+2.
   [NB: последний пункт является излишним и официально не входит в определение лямбда-исчисления для выражений, поскольку подстановка e₀ в качестве x в e₁ эквивалентна применению абстракции λx.e₁ к e₀. Он добавлен только для поддержки так называемого let-полиморфизма.]

Ничто более допустимым выражением не является.

В сторону: любой, кто уделит достаточно внимания этому вопросу, будет удивлён: «Минуточку, как мне сделать из этого какое-либо полезное выражение? Как мне получить x²+2 (или хотя бы просто 2), исходя только из изложенного? Чёрт, а что на счёт нуля? В этих правилах нет ни строчки, очевидно приводящей к выражению 0». Решением в данном случае является создание выражения в лямбда-исчислении, которое ведёт себя как 0,1,…,+,×,−,/ при корректной интерпретации. Другими словами, нам следует закодировать числа, арифметические операции, строки и т.п. в шаблоны, которые мы можем создать с помощью лямбда-синтаксиса. В этом посте есть маленький, но очень хороший раздел, посвящённый числам и арифметическим операциям. Это интереснейшая особенность лямбда-исчисления: у нас есть элементарный синтаксис, который мы можем рекурсивно определить четырьмя простыми пунктами, но он позволяет нам индуктивно доказать множество вещей в четыре основных шага, поскольку язык сам по себе обладает выразительной силой записывать числа, строки и все типы операций, которые только могут нам понадобиться.

Формализация утверждений о типах

Пусть e — любое выражение, такое что "e" — переменная в нашем мета-языка, обозначающая любое выражение из нашего базового языка. Например, такое, как любое из нижеследующих:

x
Math.pow(x,2)
[1,2].forEach ( function(x) { print(x); } )

Тогда, если t — это произвольный тип, то мы можем выразить "e имеет тип t" через
e:t

Как и e, t — это переменная в нашем мета-языке, которая может соответствовать любому типу в базовом языке (Int, String и т.д.). И так же, как для e, для t соответствие какому-либо конкретному типу не является обязательным.

Можно дать и формальное определение того, что считать типом, как мы сделали выше для выражений. Однако, абстракция в этом случае получается довольно замысловатая, так что мы этот момент опустим. Я просто обращаю ваше внимание на два ключевых положения, которые следует держать в уме:

1. Если s и t — типы, то t→s; — это тип функции с t на входе и s на выходе
2. Если r — тип, возможно составленный из других типов (подобно тому, как t→s составляется из t и s, каждый из которых, в свою очередь, потенциально можно представить композицией ещё каких-то типов), а α — переменная этого типа, то ∀α.r является типом.
   Без примера вышесказанное звучит несколько бессмысленно:

   function (x) { return x; }
   

   Эта функция имеет тип String→String. Или Int→Int. Фактически, для любого типа t её тип t→t. Мы будем говорить, что она имеет тип ∀t.t→t. Каждый из типов String→String или t→t является «монотипом». ∀t.t→t — это «политип». Функция, тождественная написанной выше, имеет абстрактный политип ∀t.t→t, который на практике означает, что для любого реального типа t она имеет тип t→t. Собирая всё вышесказанное воедино, получим вот такую компактную резюмирующую запись:
   λx.x:∀α.α→α

Формализация утверждений об утверждениях о типах

Сейчас мы хотим формализовать ветку правил о том, как от знания некоторых выражений и их типов нам перейти к выводу типов большего числа выражений. Помните, как исчисление высказываний формулирует Modus Ponens? Мы собираемся сделать нечто подобное. Например, допустим, что мы хотим формализовать следующую часть рассуждений:

Предположим, что я уже в состоянии вывести, что переменная duck имеет тип Animal.
Более того, предположим, что я вывел, что speak — метод, имеющий тип Animal -> String.
Тогда я могу вывести, что speak(duck) имеет тип String.

И любые рассуждения, укладывающиеся в такую форму, — допустимый вывод типа.

Мы формализуем это следующим образом:

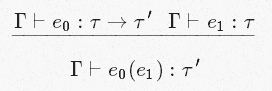
Это правило называется [App] (для наложений), и оно — одно из тех, что присутствуют в этом вопросе на StackOverflow. О нём и оставшихся правилах мы поговорим в следующем посте. А пока давайте разберёмся со всеми символами, которые нам встретились выше:

• Γ — соответствует набору положений, которые нам уже известны, или, возможно, которые мы можем предположить. Если говорить более общо, то Γ — просто размышления о некоей коллекции положений (о выражениях и их типах). И естественно в букве Γ нет ничего особенного — заглавные греческие буквы часто используют для обозначений наборов положений.
• ⊢ — «турникет», означающий, что что-то может быть выведено. Например, Γ ⊢ x:t означает, что если мы возьмём утверждение из Γ в качестве предположения/аксиомы/существующего знания, то мы можем вывести, что x имеет тип t.
• ∈ — «эпсилон», обозначает принадлежность чему-либо. x:t ∈ Γ говорит о том, что высказывание x:t принадлежит Γ.
• Та длинная горизонтальная черта. Эта линия говорит нам, что мы можем делать заключения, расположенные в знаменателе, если примем числитель в качестве исходной посылки. Что позволяет нам выразить вещи вроде: «Если мы можем вывести это и это, то мы также можем вывести то и то». Например:
  
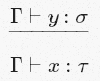
  Если мы можем вывести, что y имеет тип σ из Γ, то мы можем вывести и то, что x имеет тип τ из Γ.

Следующий шаг:

• Часть 3, в которой мы соберём всё вместе и составим представление о правилах, используемых в HM-алгоритме.

Примечание переводчика: я буду очень признательна за любые замечания в личку по поводу перевода.

Автор: AveNat

Источник