В современном мире анализа данных регрессионный анализ занимает центральное место, предоставляя мощные инструменты для выявления и количественной оценки взаимосвязей между переменными. Он позволяет исследователям и аналитикам не только описывать существующие зависимости, но и прогнозировать поведение систем на основе имеющихся данных. Одним из наиболее распространенных методов регрессионного анализа является метод наименьших квадратов, который стремится минимизировать сумму квадратов отклонений между наблюдаемыми и предсказанными значениями.
При использовании метода наименьших квадратов можно выделить два основных подхода к аппроксимации: однофакторную и двухфакторную. Однофакторная аппроксимация рассматривает влияние одной независимой переменной на зависимую, что позволяет получить простую и интуитивно понятную модель. Однако в реальных сценариях, когда возникает необходимость учитывать влияние нескольких факторов одновременно, на помощь приходит двухфакторная аппроксимация. Она позволяет более полно отразить сложные взаимосвязи и взаимодействия между переменными.
Небольшая теория аппроксимации функции методом наименьших квадратов
Есть выборка данных зависимости значений от
|
|
|
|
0 |
0 |
|
1 |
1 |
|
2 |
3 |
|
5 |
10 |
Мы знаем что, например, при равным 1,
будет равен 1, но нам нужно узнать значения между узловыми точками или узнать значение
при
равным 10. В таком случае используют регрессионный анализ. Один из вариантов получения функции по заданным точкам это аппроксимация. В конечном итоге должна быть построена функция
значения которой при
будут примерно равны значениям
.
|
|
|
|
|
0 |
0 |
≈0 |
|
1 |
1 |
≈0 |
|
2 |
3 |
≈0 |
|
5 |
10 |
≈0 |
Воспользуемся методом наименьших квадратов чтобы составить условие, при котором сумма квадратов ошибок между требуемыми значениями и результатом аппроксимируемой функции стремилась к нулю.
Т.е. в результате должны быть найдены коэффициенты функции , чтобы разница между точками
и значениями функции
.
Для функции аппроксимирования я использую числовой ряд:
На моей практике максимальную повторяемость реальной функции даст n=4. Для простоты следующего примера я буду использовать функцию n = 1 (линейную функцию )
Возьмем линейную функцию , тогда аппроксимируемая функция будет выглядеть
Далее нужно найти коэффициенты a1, a2. Для этого составим систему уравнений из частных производных по данной функции.

Возьмем производные и получим следующую систему уравнений:

Выразим из второго уравнения :
Тогда
Получившиеся формулы можно использовать для линейной регрессии, когда нужно провести усредняющую линию через всю выборку.
Подставим значения из выборки и найдем коэффициенты:
В конечном итоге мы построили регрессионную функцию, которая проходит через наши точки с минимально возможным отклонением. Обычно линейную функцию используют для определения тренда выборки, т.е. мы знаем, что с ростом значений ,
будет возрастать в 2.07 раза. Для более “точного повторения” используют функции 4 или 5 степени.
|
|
|
|
|
0 |
0 |
0 |
|
1 |
1 |
1.43 |
|
2 |
3 |
3.5 |
|
5 |
10 |
9.71 |
Реализация на платформе .NET
В конечном итоге аппроксимирования методом МНК все сводится к построению системы уравнения частных производных функции суммы ошибок между действительными значениями и значениями аппроксимируемой функции.
Для этого понадобится библиотека MathNet.Symbolics, которую можно установить через диспетчера пакетов NUuGet . Данная библиотека будет вычислять частные производные, а так же упрощать выражения.
Вычислять систему уравнений будем с помощью метода Гаусса https://en.wikipedia.org/wiki/Gaussian_elimination , реализацию можно найти в интернете или в моей библиотеке Regression в папке MathService.

static void Main()
{
//Символьное выражение членов полинома a1 * x + a2
var a1 = SymbolicExpression.Variable("a1");
var a2 = SymbolicExpression.Variable("a2");
//Аппроксимируемая выборка значений пара X Y
Dictionary<double, double> XtoY = new()
{
{ 0, 0 }, { 1, 1 }, { 2, 3 }, { 5, 10 }
};
//Построение функции F(x)
SymbolicExpression Fx = 0;
foreach (var item in XtoY)
{
var expr = item.Value + (a1 * item.Key + a2);
Fx += expr * expr;
}
//Частные производные в строковом виде
var diffA1 = Fx.Differentiate(a1).RationalSimplify(a1).ToString().Trim().Split();
var diffA2 = Fx.Differentiate(a2).RationalSimplify(a2).ToString().Trim().Split();
List<string[]> polysList = new() { diffA1, diffA2 };
// Step 1 Построение матрицы Y
double[,] Y = new double[2, 1];
for (int i = 0; i < Y.GetUpperBound(0) + 1; i++)
{
var yValues = GetArrayParseY(polysList[i]).ToArray();
for (int j = 0; j < Y.GetUpperBound(1) + 1; j++)
{
Y[i, 0] += yValues[j];
}
}
// Step 2 Построение матрицы X
double[,] X = new double[2, 2];
for (int i = 0; i < X.GetUpperBound(0) + 1; i++)
{
var xValues = GetArrayParseX(polysList[i]).ToArray();
for (int j = 0; j < X.GetUpperBound(1) + 1; j++)
{
X[i, j] += xValues[j];
}
}
// Step 3 Решение системы уравнений
Gaus gaus = new();
double[] result = gaus.Roots(X, Y);
}
/// <summary>
/// Вернуть из строк массив X значений
/// </summary>
/// <param name="strings"></param>
/// <returns></returns>
private static IEnumerable<double> GetArrayParseX(string[] strings)
{
var a = strings.Where(x => !x.Equals("+"));
var listAr = new double[2];
int sign = 1;
foreach (var stringExpression in a)
{
if (stringExpression.Equals("-"))
{
sign = -1;
continue;
}
if (!stringExpression.Contains("*a")) continue;
var str = stringExpression.Remove(0, stringExpression!.IndexOf("a", StringComparison.Ordinal)+1);
var index = int.Parse(str);
var st1r = stringExpression.Substring(0, stringExpression!.IndexOf("*", StringComparison.Ordinal));
listAr[index-1] = sign * double.Parse(st1r, CultureInfo.InvariantCulture);
sign = 1;
}
return listAr;
}
/// <summary>
/// Вернуть из строки массив Y значений
/// </summary>
/// <param name="strings"></param>
/// <returns></returns>
private static IEnumerable<double> GetArrayParseY(string[] strings)
{
var a = strings.Where(x => !x.Equals("+"));
var sign = 1;
foreach (var stringExpression in a)
{
if (stringExpression.Equals("-"))
{
sign = -1;
continue;
}
if (stringExpression.Contains("*a")) continue;
yield return sign * double.Parse(stringExpression, CultureInfo.InvariantCulture);
sign = 1;
}
}
В результате выполнения кода
SymbolicExpression Fx = 0;
foreach (var item in XtoY)
{
var expr = item.Value + (a1 * item.Key + a2);
Fx += expr * expr;
}
функция будет равна
Далее частные производные функции по -
и
-
вернут значения
Остается составить матрицу для решения системы уравнений методом Гаусса вида
Матрица A
Столбец свободных коэффициентов B
Столбец переменных
Для составления матриц из массива строк были применены методы GetArrayParseX и GetArrayParseY
В результате получаем массив коэффициентов полинома:
result[0] = 2.07
result[1] = -0.64
Таким образом можно реализовывать многофакторную регрессию, когда на входе больше, чем одно значение X. Сделать это можно перемножением полиномов друг на друга:
Возьмем полином второй степени вида:
Тогда двухфакторная аппроксимируемая функция будет выглядеть как:
Практическое применение
Рассмотрим инженерную проблему. При разработке датчика давления необходимо было построить функцию с помощью аппроксимирования, где входные данные — это код АЦП, а выходные — это давление. Выяснилось, что код АЦП давления изменяется от температуры, т.е. на одном и том же давлении код АЦП разный, следовательно для аппроксимирования необходимо было ввести еще один фактор – код температуры.
Давление на эталоне:
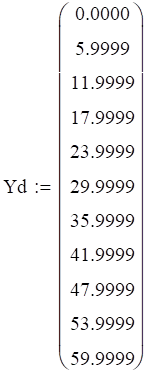
Код давления и температуры при 16 градусах:
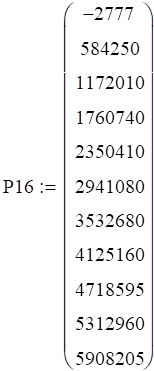
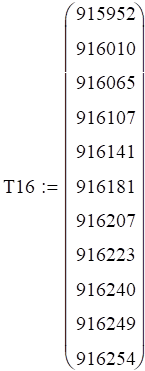
Код давления и температуры при 18 градусах


Код давления и температуры при 21 градусе


Код давления и температуры при 23 градусах


Код давления и температуры при 27 градусах
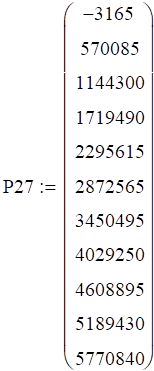

Объединим все наши коллекции:



Функция аппроксимирования полиномом третьей степени будет выглядеть:


Решим систему уравнений частных производных силами MathCad:


Приложение RegressionFromExcel
Пользоваться MathCad было не очень удобно:
· Время расчета коэффициентов могло достигать до 1 минуты
· Вносить и забирать данные в MathCad было проблематично, оператор мог ошибиться, копируя данные
Необходимо было приложение, которое бы считывало данные из листа Excel и в определенные ячейки сохраняло результаты коэффициентов. Так же сохраняло json файл с коэффициентами для определенных задач.
Так как излишний функционал с сохранением файлов востребован только на производстве я решил создать открытый проект без данных функций сохранений.
RegressionFromExcel/README.md at main · Georgiy-smr/RegressionFromExcel
В папке Exemple лежит файл TestData, в котором уже есть тестовые данные, а так же посчитанные коэффициенты. Для расчета нужно заполнить столбцы с данными и выбрать степень полинома в приложении 2 или 3. Далее приложение откроет файл, считает данные и вычислит коэффициенты, которые вставит в отдельные ячейки справа (как в примере TestData).
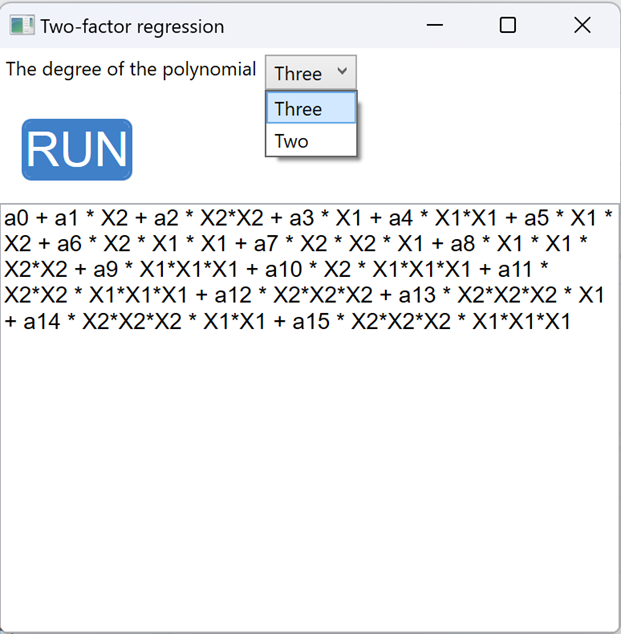
Более подробно о работе приложения будет описано во второй части.
Сравним результаты вычислений MathCad и RegressionFromExcel.


Мы видим достаточную сходимость погрешностей на уровне 2% от допустимой погрешности на диапазон преобразователя давления.
Использованная литература:
-
Кобзарь А. И. Прикладная математическая статистика. — М.: Физматлит, 2006.
Автор: mrsmirnovgd
















