Здравствуйте, дорогие читатели. В этой статье я приведу разбор того, как работает метод кластеризации К-средних на низком уровне.
Содержание: идея метода, как присваивать метки неразмеченным объектам, реализация на чистом Python и разбор кода.
Введение
Кластеризация методом K-means направлена на разбиение набора данных на k кластеров, таких, что каждый объект принадлежит кластеру с ближайшим центром кластера. Цель алгоритма — минимизировать суммарное расстояние точек кластеров от их центров.
Кластеризацию можно рассматривать как классификацию без размеченных данных (без учителя), то есть алгоритм должен классифицировать данные сам, без маркировки. Ученик должен сам отнести объекты к определенным классам, но ученик не знает, какие это могут быть классы, поэтому нужно просто сказать ему, на сколько классов нужно разделить данные объекты (на k классов). Затем ученик начинает разделять объекты по их похожести, на k классов, то есть близко похожие друг на друга объекты ученик относит к одному классу.
Формулировка задачи
Пусть имеется набор данных, состоящий из n наблюдений (объектов) ,
, k - число признаков. На основе этих данных можно сформировать исходный набор объектов, на основе которого можно произвести кластеризацию этих объектов, то есть найти центры кластеров — центры скоплений объектов разных классов.
Идея метода K-means. Необходимо определить количество кластеров k, которое нужно выделить в данных. Это значение обычно задается заранее, хотя существуют методы для его определения.
Выбираются k случайных центров кластеров для набора данных. Эти центры могут быть выбраны случайным образом или используя специальные методы инициализации.
Каждая точка данных присваивается к ближайшему центру кластера. Это делается путем расчета расстояния (обычно евклидово) между каждой точкой данных и каждым центром.
Центры обновляются как среднее значение всех точек, принадлежащих каждому кластеру. Этот шаг повторяется до тех пор, пока центры не перестанут меняться или до достижения заданного критерия сходимости. Критерием сходимости может быть качество модели либо разница изменения центров кластеров между предыдущей и текущей итерацией.
Суть метода в том, чтобы сначала найти центры скоплений объектов, а потом, на основе этих центров, классифицировать объекты путем присвоения каждому объекту в исходном наборе данных принадлежность к определенному классу (кластеру).
Разделение точек данных на кластеры
Нужно определить для каждой точки в исходном наборе данных к какому кластеру (классу) она относится. Моделью KNN будут являться метрики, алгоритмы, используемые в определении класса точек и присвоенные всем точкам их метки.
Задаем число кластеров. Возможно это можно сделать динамически, но для этого нужно придумать алгоритм, который будет делить данные на кластеры основываясь на каких-то общих закономерностях в данных, а не просто на основе расстояния.
Потом создаем центры кластеров, например, случайно. Можно задать центры кластеров по графику, на графике видно, в каких областях происходят скопления объектов, центрами кластеров будут центры этих областей.
Далее для каждой рассматриваемой точки нужно вычислить расстояние между рассматриваемой точкой данных и всеми центрами кластеров. Рассматриваем каждую точку в наборе данных, вычисляем расстояния до всех точек-центров кластеров, выбираем кластер, до которого наименьшее расстояние.
Евклидово расстояние между двумя точками вычисляется по этой формуле:
a и b — точки данных (объекты, векторы признаков), и
- элементы векторов (признаки), n — количество признаков в векторе (количество координат).
Действие алгоритма таково, что он стремится минимизировать сумму квадратов отклонений точек кластеров от центров этих кластеров:
— число точек в одном кластере,
— число элементов вектора (число признаков, координат),
— центр k-го кластера,
- i-я точка в кластере,
- j-я координата вектора
. Эта формула по сути и есть критерий сходимости алгоритма. Если значение этой функции станет меньше заданного, то алгоритм прекращает изменять центры кластеров и получается готовая модель К-средних.
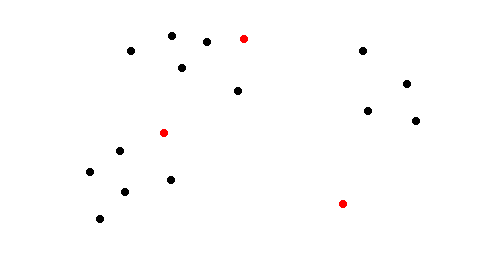
Нужно просматривать каждую точку и присваивать ей кластер, к которому она находится ближе всего, для этого нужно вычислить расстояние до каждого центра кластера. Кластеры — это красные точки на рисунке, черные точки — объекты набора данных. Каждому объекту присваивается ближайший кластер (метка ближайшей красной точки).
После каждой итерации присвоения каждой точке определенной метки, нужно обновить значения центров кластеров. Чтобы это сделать, нужно вычислить для каждого кластера среднее значение всех точек, которые относятся к рассматриваемому кластеру. Суммируем все точки по каждой координате по отдельности, а потом делим на общее число точек:
p — число координат, C — центр кластера, j — номер координаты (признака) объекта, n — число точек в кластере C, - j-я координата i-й точки кластера C. Нужно посчитать среднее значение для каждой координаты j.
Ограничения и преимущества
Алгоритм K-means не гарантирует достижения глобального минимума суммарного квадратичного отклонения. Он может застрять в локальном минимуме, зависящем от начальной инициализации центров. Поэтому можно пробовать несколько раз инициализировать центры заново.
Необходимо заранее определить количество кластеров k, которое нужно найти в данных. Для этого можно использовать дополнительные методы для определения числа кластеров.
Результат алгоритма зависит от начальной инициализации центров. Разные начальные центры могут привести к разным кластерам.
Алгоритм K-means относительно прост в реализации и понимании.
K-means может работать с огромными наборами данных и быстро обучается на новых примерах, он может быть использован для решения многих сложных задач машинного обучения.
Алгоритм K-means реализован в различных фреймворках машинного обучения.
Метод K-means является мощным инструментом для кластеризации данных, но требует тщательного выбора параметров и предварительной обработки данных для достижения оптимальных результатов.
Создание набора данных
Для задачи кластеризации нужны неразмеченные однотипные данные. Для этого используем функцию make_blobs из sklearn. Указываем число точек данных, количество центров точек (центров кластеров), число признаков (координат) и число для инициализации генератора псевдослучайных чисел.
from sklearn.datasets import make_blobs
from matplotlib import pyplot as plt
data, labels = make_blobs(n_samples=20, centers=2, n_features=2, random_state=0)
data = data.round(2)
print(list(labels))
points = [tuple(point) for point in data]
print(points)
x1_list = data[labels==0, 0]
x2_list = data[labels==1, 0]
y1_list = data[labels==0, 1]
y2_list = data[labels==1, 1]
plt.scatter(x=x1_list, y=y1_list, color='red')
plt.scatter(x=x2_list, y=y2_list, color='green')
plt.show()Получаем двумерный массив точек и одномерный массив меток — к какому классу относится каждая точка (0 или 1 для двух центров). Делаем из массива список точек и выводим. Копируем эти данные в другой файл.

Далее выделяем из данных массив для каждого признака. Массив data — двумерный первая ось массива обозначает количество точек, сами точки (объекты), вторая ось массива обозначает значения элементов точек, то есть значения координат точек, выбираем определенные значения в массиве. В качестве первого индекса указываем те элементы, которые относятся к определенному классу (к 0 или к 1), в качестве второго индекса выбираем элементы массива, которые относятся к 0 или к 1 признаку (к координате x или к координате y).
Теперь рисуем точки на графике.
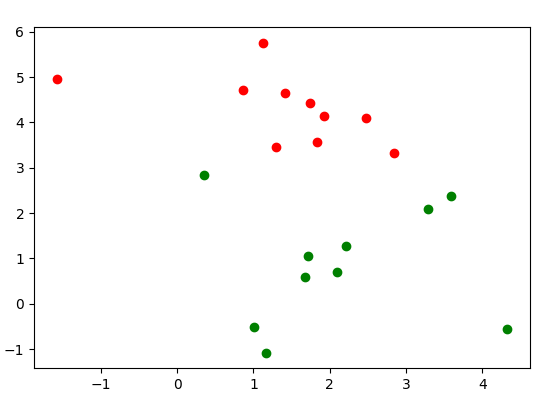
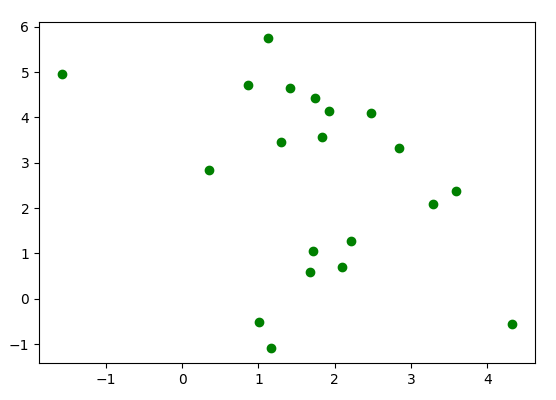
На графике видно 2 области скопления (красным и зеленым, рисунок сверху). Можно выделить два центра кластеров с примерными центрами, первый с координатами (1, 5), второй — (2.5, 1). Но если бы мы не знали, сколько всего должно быть кластеров (рисунок снизу), то можно было бы предположить, что их 3, 4 или больше. Но здесь мало объектов, чем больше объектов, тем было бы легче предположить число кластеров и их центры.
Пробная реализация
Делаем набор данных и задаем количество центров k и точки центров кластеров. Число кластеров в этом примере равно 2, а значения центров выбраны по графику.
target_labels = [0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0]
points = [(1.84, 3.56), (1.01, -0.52), (1.29, 3.45), (1.93, 4.15),
(2.84, 3.33), (1.42, 4.64), (0.87, 4.71), (2.21, 1.28),
(4.33, -0.56), (-1.58, 4.96), (2.1, 0.71), (1.17, -1.08),
(3.59, 2.37), (1.12, 5.76), (1.67, 0.6), (3.29, 2.1),
(1.71, 1.05), (0.35, 2.85), (2.47, 4.1), (1.74, 4.43)]
centers = [(1, 5), (2.5, 1)] # центры кластеров, они выбраны вручную по графикуДелаем функцию для измерения квадратичного расстояния до каждого центра от рассматриваемой точки.
def euclidean_distances_to_centers(point):
dists = []
for center in centers:
distance = 0
for i in range(2):
distance += (point[i] - center[i]) ** 2
dists.append(distance)
return distsПроходимся по каждому центру и по каждой координате, записываем значения расстояний в список dists.
Далее делаем функцию для нахождения наименьшего расстояния, то есть наименьшего элемента в списке и возвращаем его индекс.
def get_min_item_idx(distances): # найти минимальный элемент
min_dist, min_item_idx = 1000000, 0
for idx, dist in enumerate(distances):
if dist < min_dist:
min_dist = dist
min_item_idx = idx
return min_item_idxДалее делаем функцию для обновления центров кластеров. Для этого понадобится записывать принадлежность точек к кластерам, записываем это в список clusters.
clusters = [[], []]
def update_centers():
for cluster_idx, cluster in enumerate(clusters):
cluster_mean_value = [0, 0]
for point in cluster:
for i, feature in enumerate(point):
cluster_mean_value[i] += feature
for i in range(2):
cluster_mean_value[i] = cluster_mean_value[i] / len(cluster)
centers[cluster_idx] = cluster_mean_valueПроходимся по каждому кластеру (списку точек), для каждого кластера задаем новое значение центра в переменную cluster_mean_value. Проходимся по каждой точке и по каждой координате точки, суммируем каждую координату у каждой точки. Потом делим получившиеся суммы на число точек в каждом кластере. Таким образом получается среднее значение всех точек в кластере — это и есть новое значение центра кластера.
Далее делаем цикл для итеративного изменения центров.
labels = []
for _ in range(100):
clusters = [[], []]
labels = []
for point in points:
dists = euclidean_distances_to_centers(point)
min_item_idx = get_min_item_idx(dists) # получить индекс класрера
clusters[min_item_idx].append(point) # добавляем точку в ближайший кластер
labels.append(min_item_idx)
update_centers()
print(labels)output:
[0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0]В каждой итерации присваиваем каждой точке принадлежность к определенному кластеру заново, записываем метки классов для каждой точки, потом, на основе нового присвоения, обновляем центры. Смотрим какие метки получились.
Это в принципе все, что нужно для этого метода. Далее можно посмотреть на графике, какое получилось разделение.
import numpy as np
from matplotlib import pyplot as plt
data = np.array(points)
labels = np.array(labels)
x1_list = data[labels==0, 0]
x2_list = data[labels==1, 0]
y1_list = data[labels==0, 1]
y2_list = data[labels==1, 1]
plt.scatter(x=x1_list, y=y1_list, color='red')
plt.scatter(x=x2_list, y=y2_list, color='green')
plt.show()Делаем обратную процедуру, которую делали при создании набора данных, получилось почти то же самое.
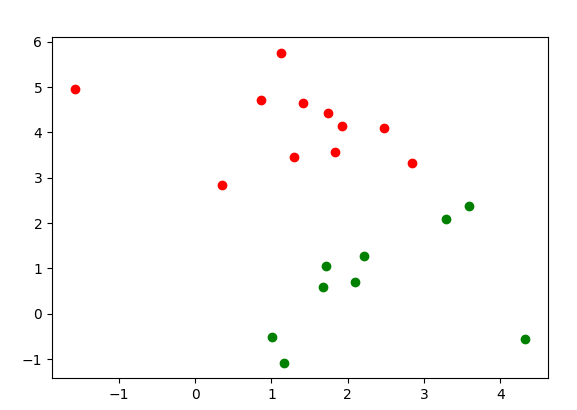
Улучшение кода
Создадим класс для модели К-средних. Перед этим переделаем функцию для измерения расстояния.
def euclidean(point1, point2):
return sum([(point1[i] - point2[i]) ** 2 for i in range(len(point1))])
def euclidean_distances(cur_point, points):
dists = []
for point in points:
dists.append(euclidean(cur_point, point))
return distsОпределяем класс. Для инициализации понадобится указать только число признаков.
class KMeans:
def __init__(self, features_num):
self.features_num = features_num
self.centers = []
self.clusters = [[] for _ in range(features_num)]Далее делаем 2 метода для того, чтобы задавать центры.
def set_centers(self, centers):
self.centers = centers
def init_centers(self, points, k):
min_value = np.min(points, axis=0) * 100
max_value = np.max(points, axis=0) * 100
self.centers = []
for _ in range(k):
x = randint(min_value[0], max_value[0]) / 100
y = randint(min_value[1], max_value[1]) / 100
self.centers.append([x, y])Центры можно будет задавать случайно или передавать заранее созданные. Случайные создаются на основе минимальных и максимальных значений признаков в точках данных. Предварительно нужно импортировать эти модули.
import numpy as np
from random import randintДалее метод для обновления центров. Тут ничего не изменилось осталось так же, как и было.
def _update_centers_(self):
for cluster_idx, cluster in enumerate(self.clusters):
cluster_mean_value = [0, 0]
for point in cluster:
for i, feature in enumerate(point):
cluster_mean_value[i] += feature
for i in range(2):
cluster_mean_value[i] = cluster_mean_value[i] / len(cluster)
self.centers[cluster_idx] = cluster_mean_valueФункция для поиска индекса минимального элемента остается почти той же. Ее можно улучшить убрав переменную min_dist и использовать сравнение по индексу наименьшего элемента, вместо того, чтобы хранить значение этого элемента.
# найти индекс минимального элемента
def get_min_item_idx(distances):
min_item_idx = 0
for idx, dist in enumerate(distances):
if dist < distances[min_item_idx]:
min_item_idx = idx
return min_item_idxТеперь метод fit, в котором будет происходить итеративное изменение центров.
def fit(self, points, epochs):
labels = []
for _ in range(epochs):
self.clusters = [[] for _ in range(self.features_num)]
labels = []
for point in points:
dists = euclidean_distances(point, self.centers)
min_item_idx = get_min_item_idx(dists) # получить индекс класрера
self.clusters[min_item_idx].append(point)
labels.append(min_item_idx)
self._update_centers_()
return self.clusters, labelsТут тоже ничего не изменилось. Добавляем возврат списков кластеров и меток из метода.
Теперь проверяем и тестируем.
kmeans = KMeans(features_num=2)
kmeans.set_centers(centers)
clusters, labels = kmeans.fit(points, 10)
print(labels)output:
[0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0]Заключение
Мы немного разобрали теорию кластеризации — рассмотрели суть метода К-средних и сделали реализацию модели. Сделали набор данных для задачи кластеризации с двумя признаками, сделали простую реализацию модели с нуля на чистом python, а потом улучшили код, сделали его более удобным для использования.
Такой обучающий урок будет полезен для начинающих и для тех, кому интересно разбираться во всем с нуля. Такой формат обучающих материалов показывает как происходит процесс разработки сложных решений от простых попыток реализации к полноценной рабочей системе, которую можно легко внедрить в какие-то программы.
Ссылка на папку с кодом из статьи на ГитХаб.
Автор: neuromancertdi






