Представьте, что управляете онлайн-магазином, предлагающим тысячи товаров.
Чтобы помочь пользователям находить нужные позиции, вы добавили строку поиска. Теперь посетители могут вводить интересующие их запросы, на что вы будете показывать им подходящие результаты.
Например, когда пользователь вводит «лето», вы можете показывать предметы вроде шортов, платьев, панам и пляжных зонтов.
Как бы вы реализовали такую систему?

Если вы используете реляционную базу данных вроде Postgres или MySQL, то можете выполнять запрос, который путём сопоставления будет находить товары, содержащие введённые пользователем слова.
Но здесь есть подвох: если пользователь ищет «лето», то БД будет исключать товары, не содержащие это слово, и вы упустите такие позиции, как «панама» или «пляжный зонт».
Чтобы более наглядно представить проблему, предположим, что у вас есть следующая таблица товаров:
| ID | Название |
| 1 | Летнее платье |
| 2 | Панама |
| 3 | Пляжный зонт |
| ... | ... |
| 999 | Зимний плащ |
Теперь выполним запрос для поиска позиций, в названии которых содержится «лето» (в оригинале summer — прим. пер.):
SELECT * FROM products WHERE name LIKE '%summer%';
=> Found 1 result
=> Product(id=1 name="Summer dress")Всё верно, был найден 1 результат — «Летнее платье». Но как же «Панама» и «Пляжный зонт»? Возможно, именно эти вещи ищет пользователь, а в результатах поиска они отсутствуют.
И здесь нет ошибок в написании, поэтому нечёткий поиск (fuzzy search) не поможет. База данных не находит эти товары, потому что не понимает, что они в более общем смысле относятся к «лету».
Вот здесь и приходят на выручку векторные базы данных.
Содержание
- Начнём с основ — что такое вектор?
- Что такое векторная база данных?
- Примеры использования
- Принцип работы векторных баз данных
- Простейший векторный поиск на чистом Python
- Поиск сходств и метрики расстояния
- Уменьшение размерности
- Список векторных баз данных
Начнём с основ — что такое вектор?
В нашем случае вектор — это просто список чисел. Он подобен координатам в многомерном пространстве, где каждое измерение представляет отдельный признак элемента.

Вектор может выражать что угодно: слово, продукт, изображение и даже прошлые взаимодействия пользователя с вашим приложением.
Например, если вы будете рекомендовать посетителям товары, то можете использовать для их представления вектор с сотнями измерений, каждое из которых будет выражать отдельный аспект того или иного товара (цвет, размер, цену, сезонность и так далее).
В этом случае вы можете сравнивать такие векторы для поиска схожих товаров, даже если они не будут содержать одинаковые ключевые слова.
Что такое векторная база данных?
Векторная база данных — это простая база данных, оптимизированная под хранение и поиск векторов, даже таких, которые состоят из сотен и тысяч измерений.
Когда вы запрашиваете вектор, вместо поиска точных совпадений, он находит элементы на основе их приближённости к запросу.
Например, в нашем сценарии векторы «лето» и «панама» окажутся рядом, а вектор «зимний плащ» будет отдалён.

Примеры использования
Векторные базы данных можно использовать в очень разных ситуациях. Вот несколько примеров:
- Контекст для чат-ботов: получение программой подходящих FAQ, документов или прежних бесед для предоставления более эффективных ответов. Подробнее о генерации ответов, дополненных результатами поиска (retrieval-augmented generation, RAG), читайте здесь.
- Контекстный поиск: поиск, при котором сопоставление запроса производится не по словам, а по смыслу.
- Персонализация: создание рекомендаций на основе того, что понравилось пользователям с аналогичными интересами.
- Память для LLM: в качестве внешней памяти, помогающей LLM (большим языковым моделям) вспоминать прошлые взаимодействия пользователя или его данные.
- Обратный поиск изображений: поиск похожих изображений на основе контента или стиля.
- Рекомендация музыки: предложение песен на основе предпочтений пользователя или аналогичных произведений.
По сути, всякий раз, когда вам нужно найти элементы на основе сходства или контекста, это можно сделать с помощью векторной базы данных.
Принцип работы векторных баз данных
В общем виде схема работы векторных баз данных выглядит так:
▍ 1. Создание эмбеддингов

На первом этапе вы преобразуете данные (текст, изображения и так далее) в векторы, используя подходящую модель вроде OpenAI или Cohere, либо библиотеку вроде SentenceTransformers.
▍ 2. Индексация векторов

База данных будет сохранять векторы удобным для их последующего запроса способом. Зачастую это делается с помощью техники, называемой «приближенный поиск ближайших соседей» (approximate nearest neighbors, ANN), чтобы БД не приходилось сравнивать между собой все векторы в датасете.
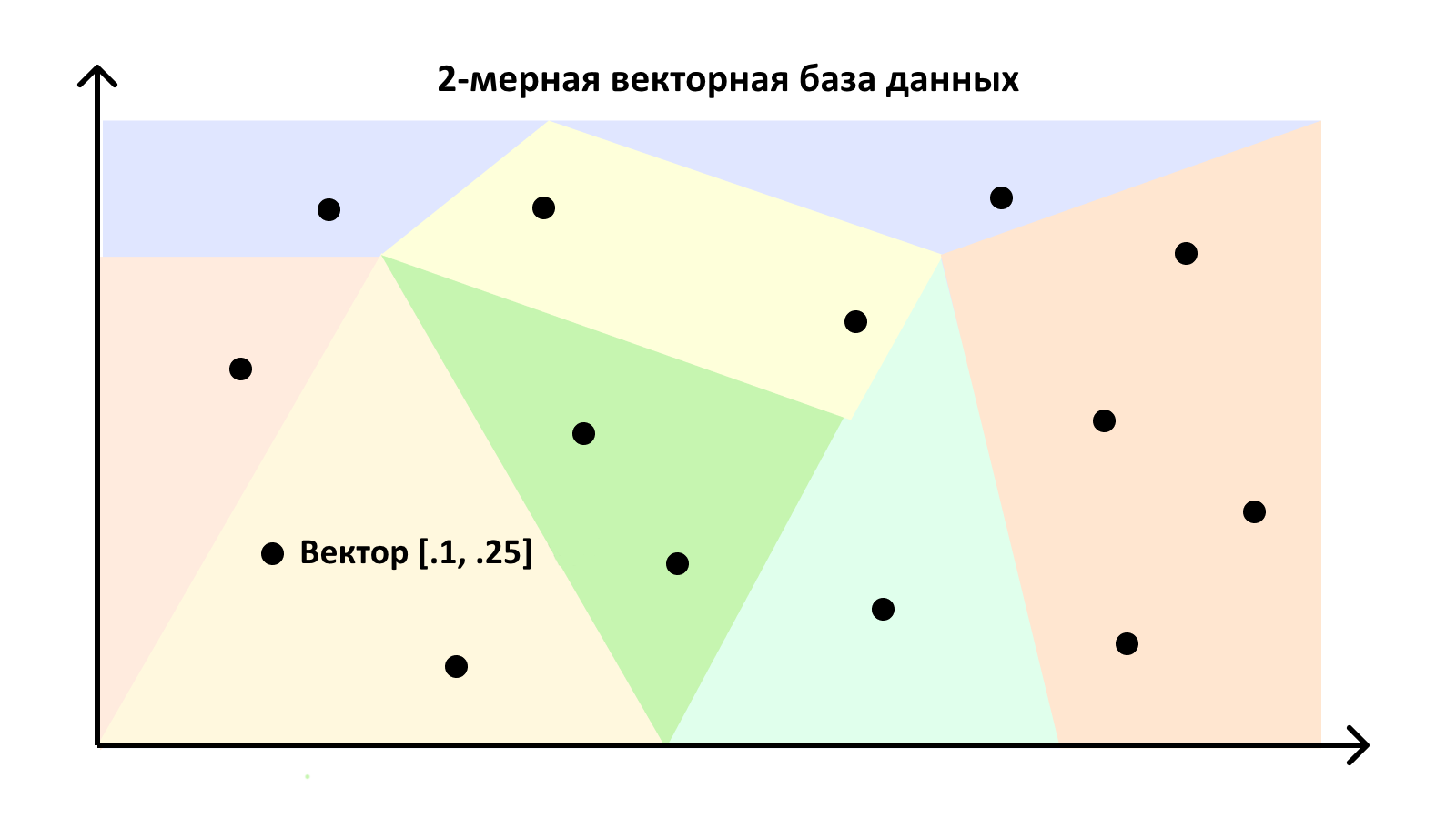
Можно представить этот механизм в виде гигантской карты, на которой, чем ближе находятся две точки, тем больше между ними сходство. База данных делит такие карты на области, чтобы быстро находить точки, наиболее приближенные к конкретному запросу.
▍ 3. Векторный поиск

При выполнении запроса ваш ввод преобразуется в вектор, и база данных ищет область карты, к которой полученный вектор относится. Обнаружив искомую область, она сможет быстро найти векторы, находящиеся рядом с вашим.
Это очень упрощённое представление, но оно позволяет понять внутренний принцип работы векторных баз данных.
Простейший векторный поиск на чистом Python
А теперь взглянем чуть уже. Если ваш датасет достаточно невелик, то поначалу векторную базу данных использовать не обязательно. Вы можете просто перебирать все имеющиеся векторы и вычислять показатель их сходства с запросом вручную.
В качестве примера я приведу скрипт Python, который ищет самые близкие к запросу векторы, используя коэффициент Отиаи:
import math
# Пример вектора запроса
QUERY_VECTOR = [0.2, 0.3, 0.8]
# Пример базы данных
VECTOR_DATABASE = [
[0.1, 0.2, 0.9],
[0.8, 0.7, 0.3],
[0.4, 0.1, 0.5]
]
def cosine_similarity(vec1, vec2):
dot_product = sum(a * b for a, b in zip(vec1, vec2))
magnitude1 = math.sqrt(sum(a * a for a in vec1))
magnitude2 = math.sqrt(sum(b * b for b in vec2))
return dot_product / (magnitude1 * magnitude2)
# Поиск самого близкого к запросу вектора
similarities = [cosine_similarity(QUERY_VECTOR, vec) for vec in VECTOR_DATABASE]
most_similar_index = max(range(len(similarities)), key=lambda i: similarities[i])
# Вывод самого близкого вектора
print(f"Most similar vector: {VECTOR_DATABASE[most_similar_index]}")
print(f"Similarity score: {similarities[most_similar_index]}")Этот скрипт демонстрирует принцип работы механизма поиска векторов. На практике по мере роста набора данных вам потребуется более эффективный способ их поиска и сравнения. В этом случае подходит выделенная векторная база данных.
Поиск по сходству и метрики расстояния
Далее речь пойдёт о том, как векторные базы данных измеряют сходство. Вот два популярных способа:
- Евклидова метрика: подразумевает измерение прямого расстояния между двумя векторами. Обычно используется в задачах кластеризации и классификации, когда важна величина вектора (например, для вычисления GPS-координат или значений RGB).
- Коэффициент Отиаи: используется для измерения косинуса угла между двух векторов. Полученная величина представляет, насколько схожими векторы являются по направлению (но не величине). Эта техника зачастую используется в системах оценки схожести текста или рекомендательных механизмах.
Но существует и много других метрик расстояния. Итоговый выбор будет зависеть от ваших данных и решаемой задачи.
Уменьшение размерности
Ниже я вкратце опишу типичную проблему векторных баз данных, называемую «проклятие размерности».
Когда вы работаете с векторами высокой размерности, бывает сложно эффективно реализовать их поиск и сравнение. Вдобавок к этому, вы можете сталкиваться с проблемами переобучения и шума.
Справиться с подобными сложностями можно при помощи техник уменьшения размерности, таких как метод главных компонент (principal component analysis, PCA) или t-SNE. Их применение позволит сократить число измерений, сохранив наиболее важную информацию.
К примеру, вы можете сократить 1000-мерный вектор до 100-мерного так:
from sklearn.decomposition import PCA
# Пример эмбеддингов с 1000 измерений.
vectors = [
[0.1, 0.2, ...],
[0.8, 0.7, ...],
[0.4, 0.1, ...]
]
# Сокращение векторов до 100 измерений.
pca = PCA(n_components=100)
reduced_vectors = pca.fit_transform(vectors)
print(reduced_vectors)Это типичная техника, используемая в машинном обучении и анализе данных для упрощения их обработки. Есть и другие техники, которые в этой статье я разбирать не стану, но вам для изучения рекомендую: автокодировщик, отбор признаков и регуляризация.
Список векторных баз данных
Завершим же мы эту тему списком доступных для ознакомления векторных баз данных. Отмечу, что список этот далеко не исчерпывающий, но послужит хорошей отправной точкой:
- Qdrant: опенсорсная векторная БД с акцентом на производительности.
- pgvector: если вы уже используете Postgres, то она станет простым апгрейдом. Также рекомендую pgvectorscale, которая оптимизирует обработку больших датасетов и ускоряет выполнение запросов.
- sqlite-vec: дополняет SQLite возможностями векторного поиска.
- Pinecone: полностью управляемая и простая в освоении.
- Convex: база данных реального времени с поддержкой эмбеддингов.
- Faiss: библиотека для поиска по сходству, разработанная Facebook.
- MeiliSearch: опенсорсный механизм поиска с поддержкой векторов.
- Chroma: простая в использовании опенсорсная векторная БД.
Автор: Bright_Translate






