В четвёртой серии цикла о графических вероятностных моделях (часть 1, часть 2, часть 3) мы продолжим разговор о том, как справляться со сложными фактор-графами. В прошлый раз мы изучили алгоритм передачи сообщений, который, правда, работает только в тех случаях, когда фактор-граф представляет собой дерево, и в каждом узле можно без проблем пересчитать распределения грубой силой. Что делать в по-настоящему интересных случаях, когда в графе есть большие содержательные циклы, мы начнём обсуждать сегодня – поговорим о паре относительно простых методов и обсудим очень мощный, но непростой в использовании инструмент – вариационные приближения.
Краткое содержание предыдущей серии
Для начала вспомним, что такое фактор-граф, который мы обсуждали в прошлый раз. Это двудольный граф, в котором два сорта вершин соответствуют переменным и функциям. Каждая функция связана с теми переменными, от которых она зависит, а сам граф задаёт разложение большой функции в произведение маленьких. В прошлый раз мы подробно рассматривали очень простой пример фактор-графа – линейную цепочку узлов
,
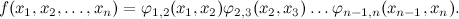которая соответствует разложению
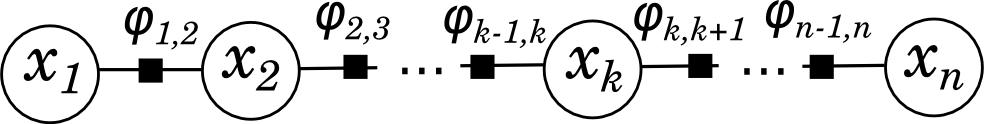
Алгоритм передачи сообщений, суть которого мы увидели на этом примере, работает практически без изменений в любом фактор-графе, который представляет собой дерево: сообщения передаются от листьев к дереву, сходятся в корне дерева (которым может быть любой узел), а потом расходятся обратно. В результате каждая вершина графа получает сообщения от всех своих соседей, после чего может легко вычислить сумму исходного разложения по всем переменным, кроме себя самой (подсчитав тем самым своё маргинальное распределение).
Однако в реальной жизни далеко не все полезные вероятностные модели описываются графами-деревьями. Один такой пример мы уже рассматривали в нашем цикле статей – это модель LDA (latent Dirichlet allocation), которая очень полезна для автоматического анализа текстов (text mining) и в виде байесовской сети выглядит так:
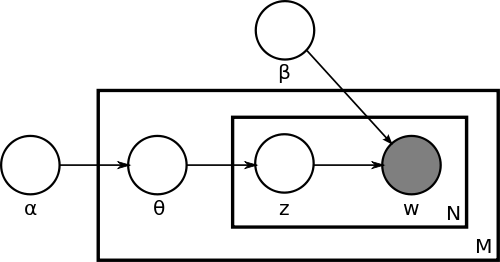
Напомню, что модель, изображённая на этой картинке, генерирует новый документ длины N так:
- выбрать вектор
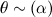— вектор «степени выраженности» каждой темы в документе; - для каждого из N слов w:
- выбрать тему
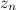по распределению 
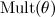; - выбрать слово
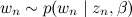с вероятностями, заданными в β.
- выбрать тему
Картинка выглядит так просто, потому что использует так называемые «плашки» (plates) – каждый прямоугольник на самом деле подразумевает несколько копий всего, что в нём изображено. Например, если полностью нарисовать фактор-граф LDA, скажем, для двух документов, в одном из которых два слова, а в другом три, уже на этом этапе получится довольно внушительная структура (чтобы не загромождать картинку окончательно, я не стал подписывать функции):
Как видите, циклов здесь много, и они происходят от того, что одни и те же параметры α и β используются многократно для получения разных наблюдений. Такая ситуация, естественно, встречается очень часто – собственно, это и есть основная постановка задач в машинном обучении: в предположении, что параметры распределения одни и те же, оценить их или предсказать последующие наблюдения. Поэтому циклы в графических моделях – не баг, а фича. И мы сейчас попробуем поговорить о том, как эту фичу реализовать. Сразу предупреждаю, что наше повествование постепенно заходит во всё более математически сложные области; уже сегодня я буду больше махать руками, чем что-то доказывать, а дальше мы уже будем переходить к конкретным примерам. Желающим изучить материал подробнее рекомендую посмотреть отличную книгу Бишопа о байесовском выводе, книгу Hastie et al. о машинном обучении, курс по графическим моделям на Coursera и другие источники – в наше время в источниках уже нет недостатка.
А мы будем потихоньку справляться с циклами. Сегодня я рассмотрю несколько методов, которые позволяют справиться с циклами в некоторых случаях, и, когда они работают, обычно удобнее и вычислительно проще их и использовать. А в другой раз мы поговорим о более общем методе, связанном с сэмплированием по Гиббсу (точнее, сэмплированием, основанным на цепях Маркова – Markov chain Monte Carlo).
Заменить цикл на вершину
Иногда цикл можно безболезненно заменить на одну вершину, просто увеличив число переменных у соответствующей функции. Например, попался вам где-то в фактор-графе треугольник:
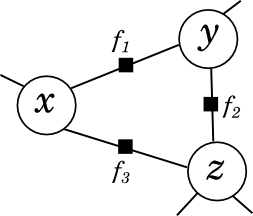
Как мы уже знаем, он означает, что в разложении встречается
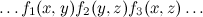
В большинстве случаев такой треугольник можно безболезненно заменить новой функцией
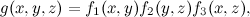
и цикл пропадёт:
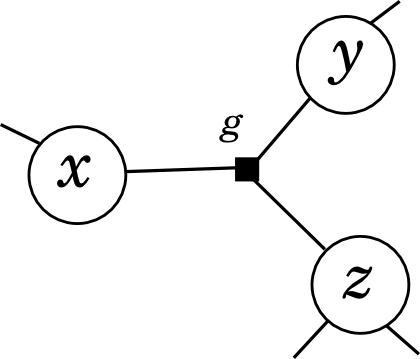
Недостаток этого метода понятен – с ростом числа аргументов у функции вычисления, как правило растут экспоненциально (если не растут, то и задача маргинализации особой сложности не представляет, так что не надо и городить огород с графическими моделями). Поэтому справиться так можно только с маленькими циклами. А в практически важных задачах циклы как раз часто очень большие, проходящие по всему диаметру графа: посмотрите хотя бы на циклы в модели LDA, проходящие от α до β и обратно. Поэтому это «игрушечный» метод, в реальности он, как правило, неприменим – точнее, модели обычно сразу строят так, как будто бы его уже применили во всех возможных случаях.
Алгоритм передачи сообщений
Первый практически важный метод, которым можно воспользоваться, если алгоритм передачи сообщений неприменим – это, естественно, алгоритм передачи сообщений. :) Конечно, для циклов он, формально говоря, не работает – неоткуда начать, нет листьев. Поэтому здесь используют модификацию алгоритма передачи сообщений, известную как loopy belief propagation:
- отправить из каждой вершины-переменной в каждую вершину-функцию сообщение, тождественно равное 1;
- дальше использовать обычный алгоритм передачи сообщений.
Конечно, такое издевательство над алгоритмом передачи сообщений проходит не вполне безболезненно. Во-первых, он из точного становится приближённым; если раньше достаточно было прогнать сообщения по каждому ребру по одному разу в каждую сторону, то теперь сообщения пересылаются сразу по всем рёбрам и постепенно меняются; мы надеемся, что со временем эти сообщения перестанут меняться (сойдутся к некоторым значениям), и тогда мы возьмём эти значения как ответ.
Во-вторых, даже эта надежда не всегда оправдывается. Легко построить пример, в котором алгоритм передачи сообщений не сможет никуда сойтись – например, он может осциллировать между двумя фиксированными состояниями (оставим это как упражнение читателю, построить такой пример не очень сложно). С другой стороны, он может всё-таки сойтись, но сойтись к неправильному ответу (здесь нетривиальные примеры уже более технически сложные, давайте я дам вам слово джентльмена, что они существуют). Однако есть ряд работ, в которых даны условия, при которых loopy belief propagation сходится куда надо; эти условия часто выполняются, да и когда они не выполняются, алгоритм часто на практике работает как надо.
Отмечу здесь на будущее: loopy belief propagation выглядит очень похоже на сэмплирование по Гиббсу, которым мы займёмся в следущий раз; однако на самом деле между методами есть принципиальная разница. Главная разница заключается в том, что loopy belief propagation – детерминированный алгоритм, и если вам с ним не повезло, то ничего сделать уже не получится. А методы сэмплирования принципиально рандомизированы, и даже если один из запусков сэмплера приводит к неверным результатам, в большинстве других запусков дело, скорее всего, наладится. Но об этом позже.
Вариационные приближения
Последний метод борьбы с чрезмерно сложными моделями, о котором я хотел поговорить сегодня, – это вариационные приближения. Скорее всего, если у вас физическое или матфизическое образование, вы лучше меня понимаете, что такое вариационное приближение; но я всё равно попробую объяснить на пальцах. Суть метода такова: мы пытаемся добавить новых степеней свободы к исходной задаче и представить её в виде задачи оптимизации (по новым, искусственно введённым параметрам).
Чтобы понять, что это всё вообще значит, рассмотрим классический простейший пример – представим функцию логарифма в вариационном виде:
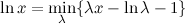
(это равенство легко проверить, просто взяв производную по λ – проверьте!).
Теперь это семейство линейных функций, каждая из которых даёт верхнюю оценку на логарифм (иными словами, логарифм – огибающая этого семейства), и если удастся хорошо выбрать λ, то получатся хорошие оценки в интересующей нас области. Выглядит это примерно так (картинка из статьи [Jordan et al., 1999]):
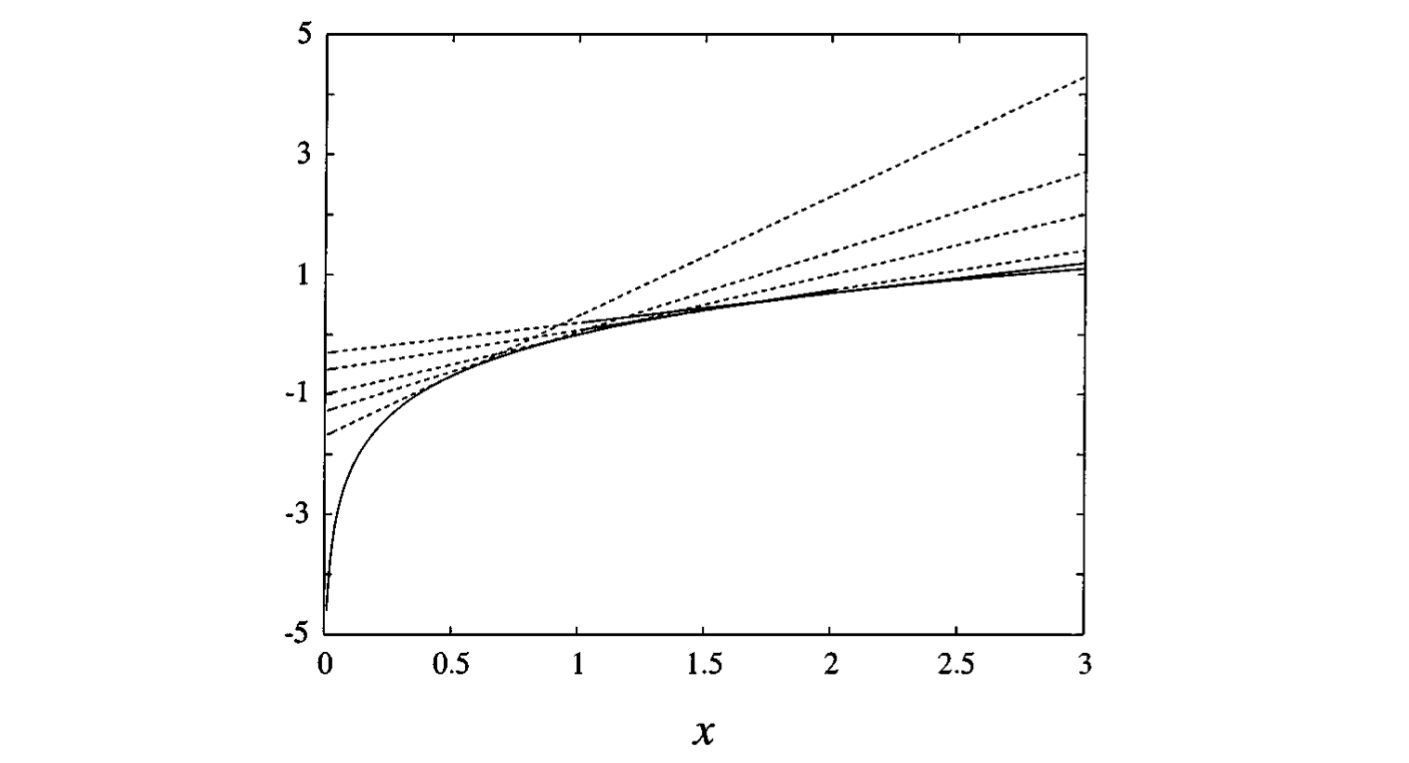
Здесь было очень важно, что логарифм — вогнутая функция, иначе так не получилось бы. Но часто можно добиться свойств выпуклости по-другому. Второй пример — логистическая функция:
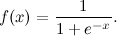
Она не выпуклая и не вогнутая, но она лог-вогнутая, т.е.
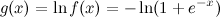
является вогнутой функцией от x. Поэтому для g(x) можно найти линейные оценки:
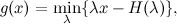
где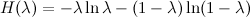 
, т.е. обычная энтропия. Опять же, упражнение – проверьте это (что-то многовато сегодня упражнений, но что поделать). Дальше можно взять экспоненту (она монотонна, т.е. неравенство сохранится):
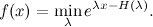
В частности, мы получаем семейство верхних оценок:
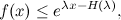
и чем лучше мы выберем λ, тем лучше оценим. Графически это выглядит так (картинка из статьи [Jordan et al., 1999]):
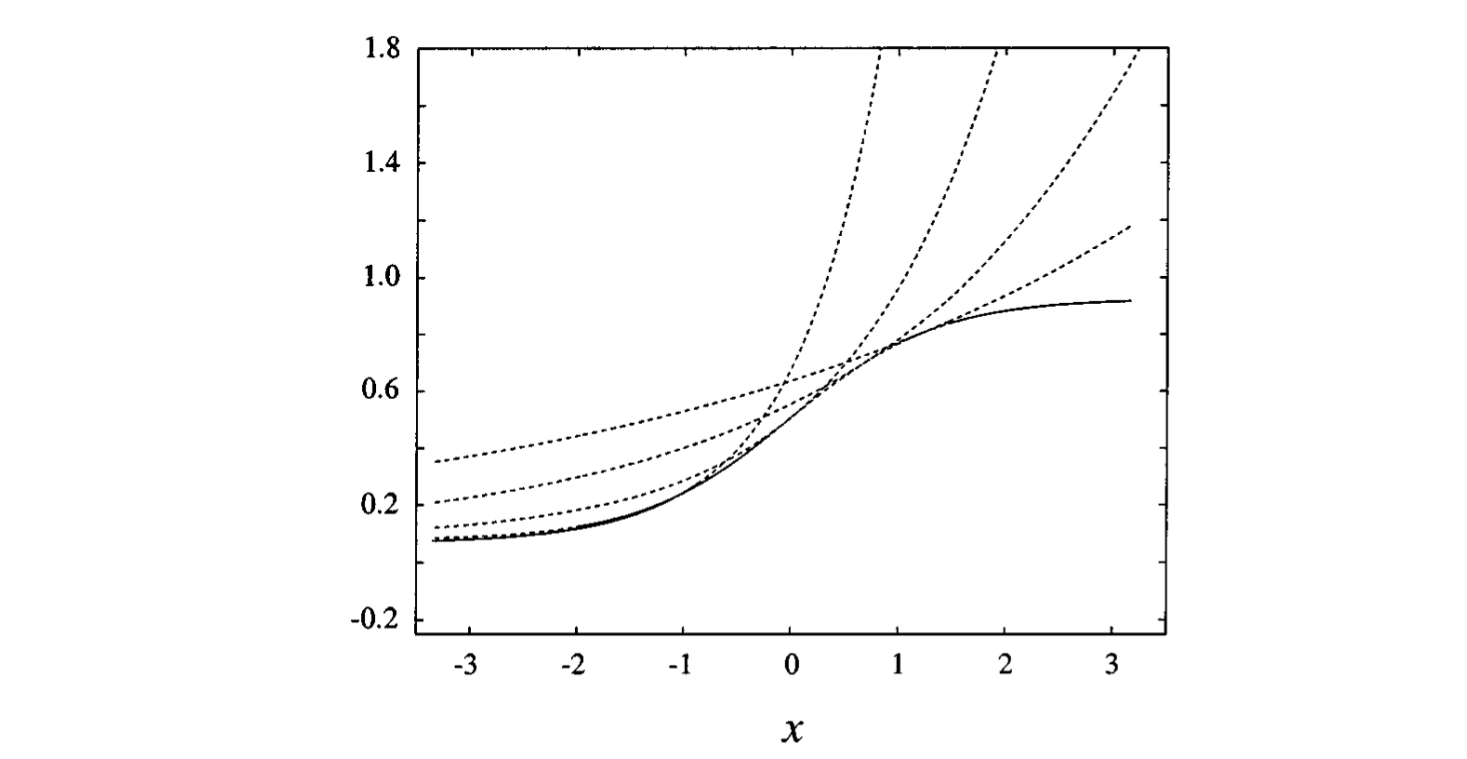
При чём же здесь графические модели? А вот при чём. Напомню, что мы занимаемся решением задачи маргинализации: по данной модели и, возможно, значениям некоторых переменных найти маргинальное распределение вероятностей
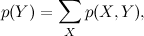
где X и Y – подмножества переменных (обычно Y – маленькое подмножество, часто одна интересующая нас переменная). Пусть просуммировать совместное распределение в лоб не получается (в частности, когда мы рисуем фактор-граф, в нём получается много циклов). Если мы сможем найти вариационные оценки для совместного распределения, мы получим оценку
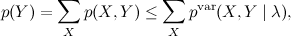
где λ – вариационные параметры. Здесь предполагается, что мы, конечно, были не дураки и выбрали их специально так, чтобы теперь суммирование было провести легко. Тогда в результате получается функция от относительно небольшого числа переменных, Y и λ, и исходная задача маргинализации превращается в задачу минимизации этой функции по λ, что часто сделать гораздо проще.
Если же посмотреть на всё происходящее с немножко другой стороны, то суть вариационных приближений можно представить так:
- у нас есть сложное распределение, с которым непонятно чего делать;
- мы находим класс простых распределений, с которыми жить легко и приятно;
- а потом стараемся в этом классе найти распределение, которое наиболее похоже на наше исходное сложное распределение (оптимизируя по вариационным параметрам).
Минусов здесь два: во-первых, ответ получается приближённый, т.к. даже при хорошем решении задачи оптимизации не всегда вариационные оценки так удачно касаются нужной функции, как на картинках выше, иногда остаётся зазор (т.е. класс простых распределений заметно отстоит от нужного сложного распределения). Но это не так страшно, никто и не ожидает точного решения в сложных случаях. Более важная проблема в том, что вариационные методы – это всегда «ручное» решение, их не автоматизируешь: надо найти удачную форму вариационной оценки, которая легко суммируется и которую потом можно оптимизировать. Такие формы найдены для некоторых классов моделей, но в общем для каждой серьёзной модификации научный поиск начинается заново (хотя, конечно, не с нуля).
Так, например, в разработанной схеме вариационного приближения для модели LDA, графическая модель из изображённой выше (в первом разделе статьи) превращается вот в такую (картинка из статьи [Blei, Jordan, Ng, 2003]):
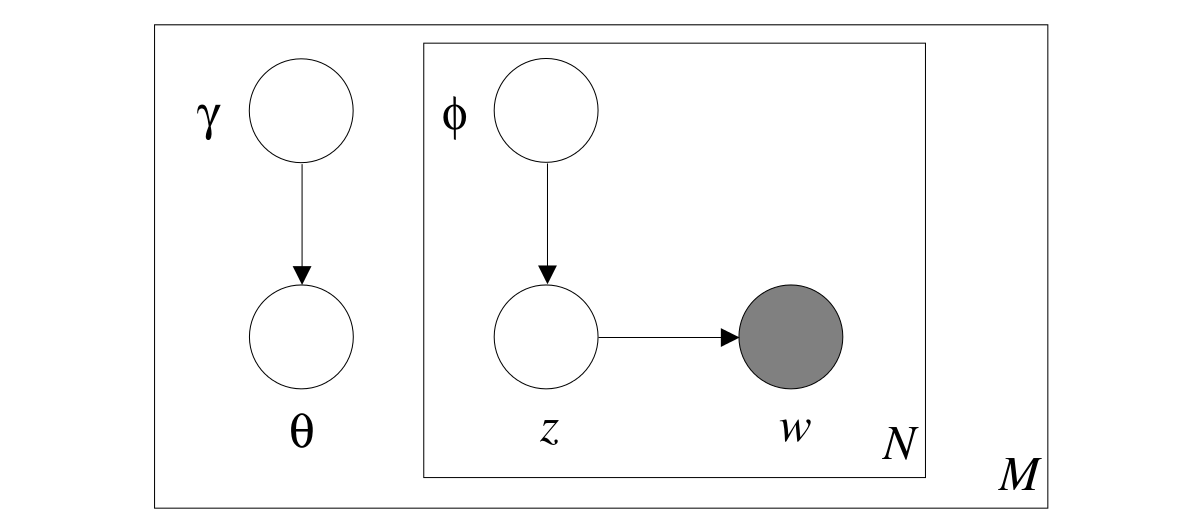
Как видите, никаких циклов тут уже не осталось, и задача маргинализации получила приближённое решение, которое сводится к задаче оптимизации по вариационным параметрам γ и φ.
Однако для LDA есть и довольно простая схема сэмплирования по Гиббсу; разница здесь в том, что сэмплирование по Гиббсу – это в данном случае очень простой и прямолинейный метод, его легко понять и запрограммировать (точнее говоря, легко понять, как он работает, а вот почему он работает – это уже чуть более тонкий вопрос), а вариационный метод сложнее, но алгоритм получается в результате эффективнее. В результате, как правило, статьи о различных расширениях LDA делятся на два класса: если авторам удаётся найти вариационное приближение, они дают схему такого приближения и соответствующий алгоритм вывода; если не получается – ограничиваются схемой сэмплирования по Гиббсу, которая, как правило, для любых расширений получается более-менее автоматически.
В следующий раз мы продолжим знакомство с методами вывода в сложных вероятностных моделях и поговорим как раз о сэмплировании – на данный момент наиболее универсальном инструменте приближённого вывода.
Автор: snikolenko
