Нейронные сети (инференс MNIST) на «3-центовом» микроконтроллере

Вдохновившись на удивление высокой производительностью нейронных сетей и обучением с учётом квантования на микроконтроллере CH32V003, я захотел выяснить, как далеко эту идею можно развить. Насколько можно сжать нейронную сеть с сохранением высокой точности тестов на датасете MNIST? Когда речь идёт о крайне дешёвых микроконтроллерах, сложно предположить что-то более подходящее, чем 8-битные Padauk.

Эти устройства оптимизированы под простейшие и самые дешёвые приложения из доступных. Самая мелкая модель серии, PMS150C, оснащена однократно программируемой памятью в 1024 13-битных слова и 64 байтами RAM — на порядок меньше, чем в CH32V003. Кроме того, эта модель в противоположность намного более мощному набору инструкций RISC-V содержит коммерческий регистр-аккумулятор на основе 8-битной архитектуры.

Возможно ли реализовать механизм инференса MNIST, способный классифицировать рукописные числа, также и на PMS150C?

Я использовал образцы MNIST на CH32V003, понизив их разрешение с 28х28 до 16х16, чтобы каждый образец занимал 256 байтов хранилища. Это вполне приемлемо, если доступно 16 КБ флэш-памяти, но когда объём всей ROM составляет 1024 слова, получается перебор. Поэтому я начал с даунскейлинга датасета до 8х8 пикселей.

На изображении выше представлено несколько образцов из датасета в обоих разрешениях. При 16х16 цифры по-прежнему легко различимы. При 8х8 можно угадать большинство чисел, но значительная часть информации утрачивается.

Удивило то, что можно по-прежнему обучить модель МО (машинное обучение) с поразительной точностью распознавать эти числа даже с низким разрешением. Важно помнить, что тестовый датасет содержит 1 000 изображений, которые модель во время обучения не видит. Для очень небольшой модели единственным способом точно распознать эти изображения является определение общих паттернов — ёмкость модели слишком ограничена, чтобы «запоминать» целые цифры. Я обучил несколько комбинаций нейронной сети, чтобы понять компромисс между занимаемой сетью памятью и достигаемой точностью.

▍ Исследование параметров

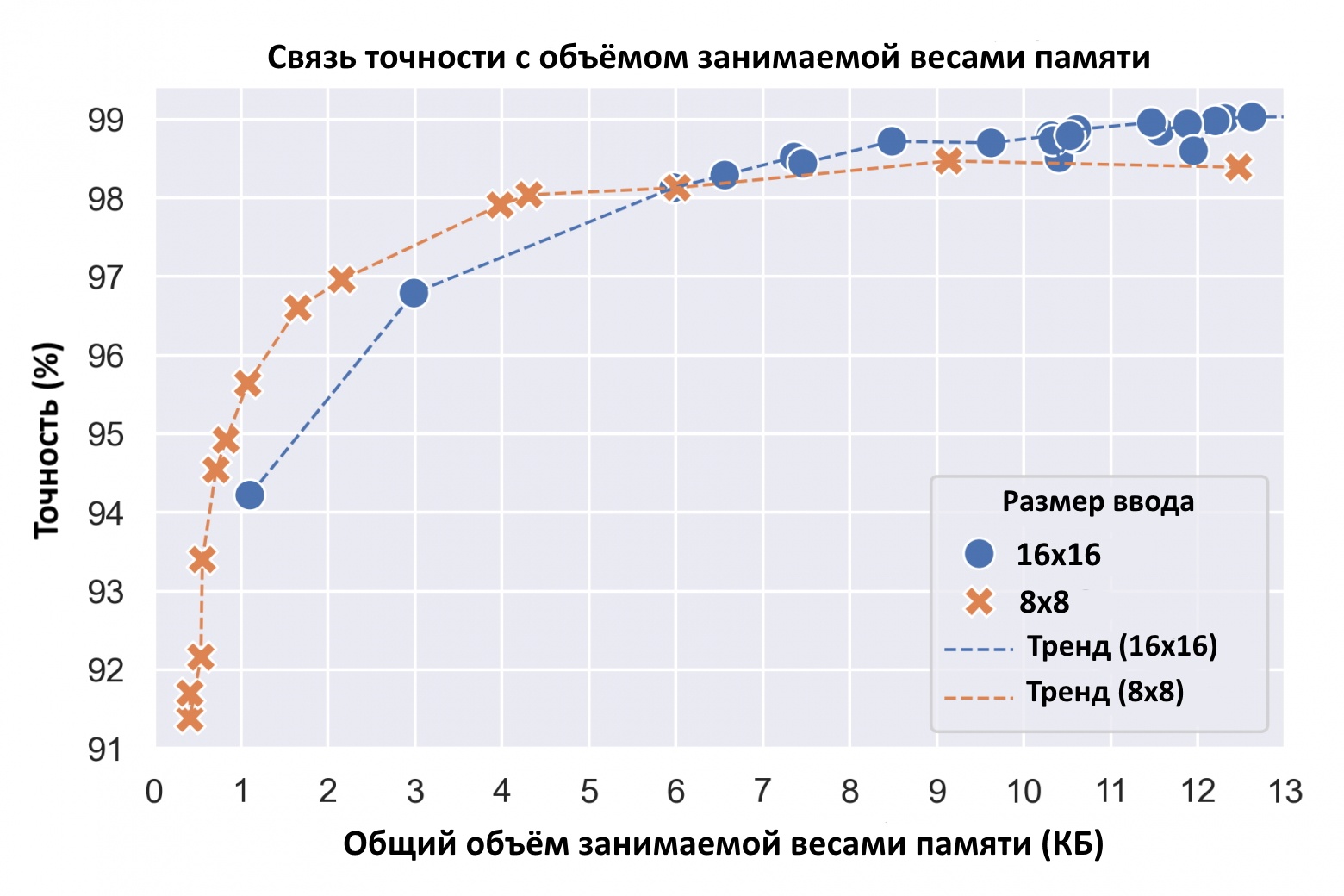
На графике выше результат моих экспериментов с гиперпараметрами, где я сравнивал модели с разными конфигурациями весов и уровнями квантования от 1 до 4 бит для входных изображений с разрешением 8х8 и 16х16. Самые мелкие модели нужно обучать без аугментации данных, поскольку иначе они не сойдутся.

Опять же, есть отчётливая связь между точностью тестов и объёмом занимаемой сетью памяти. Увеличение выделяемой под модель памяти до определённой точки повышает её точность. Для изображений 16х16 максимум можно достичь 99%, а для образцов 8х8 — 98,5%. И это всё равно довольно впечатляет, учитывая значительную потерю информации в случае 8х8.

В небольших моделях, напротив, размер 8х8 обеспечивает лучшую точность, чем 16х16. Причина в том, что в малых моделях доминирует первый слой, а его размер для ввода 8х8 уменьшается в 4 раза.

Удивительно, но тестовую точность выше 90% можно получить даже на моделях в полкилобайта. То есть такая сеть вполне впишется в программную память микроконтроллера.

Теперь же, установив, что технически мой замысел вполне реализуем, мне нужно было дополнительно всё подстроить, чтобы вписаться в ограничения МК.

▍ Обучение целевой модели

Поскольку объём RAM ограничен 64 байтами, структура модели должна использовать при выводе минимум скрытых параметров. Я выяснил, что можно использовать слои достаточно небольшой ширины 16. Это сокращает размер буфера во время вывода до всего 32 байт, по 16 для входного буфера и выходного, оставляя 32 байта для других переменных. При этом ввод 8х8 считывается непосредственно из ROM.

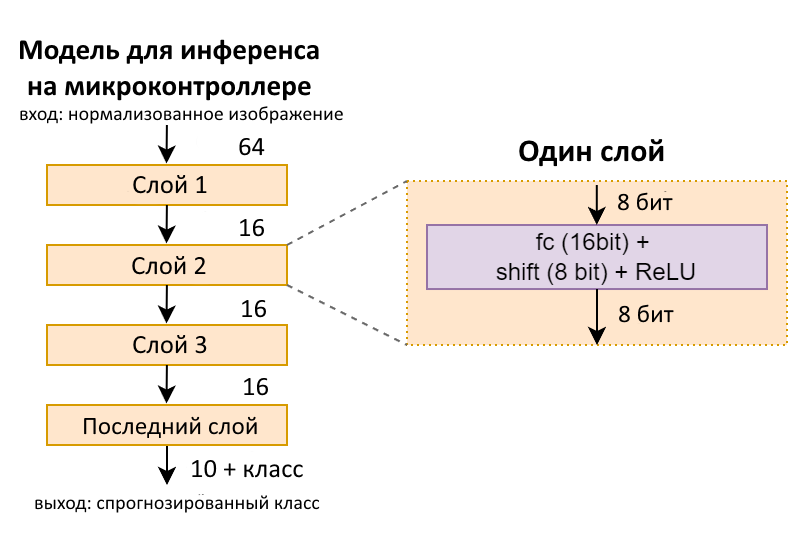
Кроме того, я использовал 2-битные веса с неравномерным разрывом (-2, -1, 1, 2), чтобы получить упрощённую реализацию кода вывода. Я также пропустил нормализацию слоёв, использовав вместо неё постоянный сдвиг для изменения масштаба активаций. Правда, все эти изменения несколько снизили точность. Итоговая структура модели показана ниже.

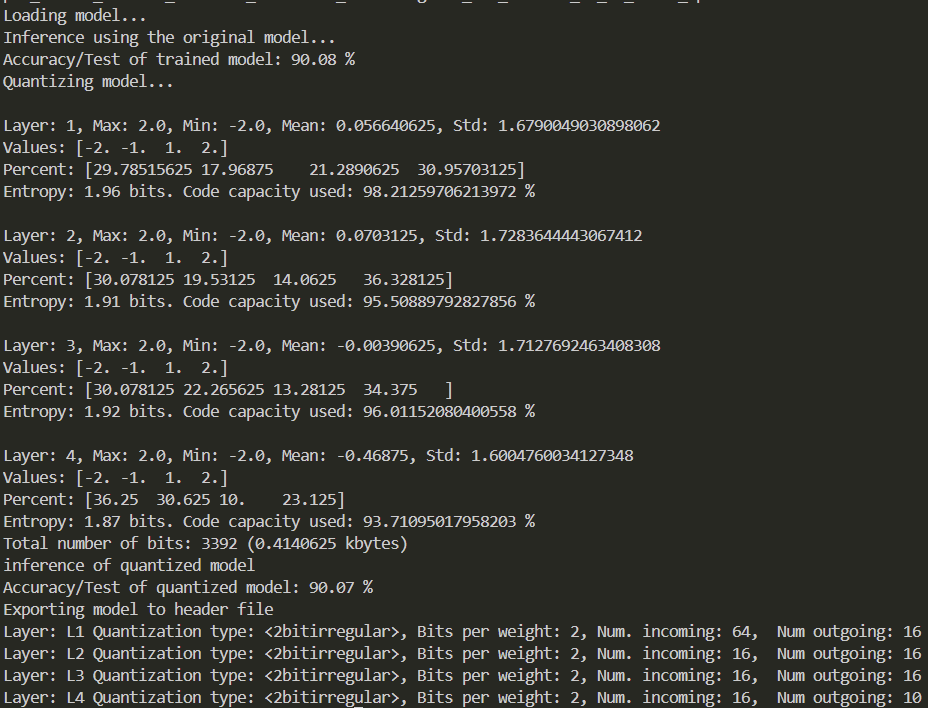
Как видно из приведённого далее вывода, в итоге моя модель продемонстрировала точность 90,07%, используя 1696 весов, занимающих 3 392 бита (0,414 КБ). Следом за выводом показано окно с весами первого слоя обученной модели, которые непосредственно маскируют признаки тестовых изображений. В отличие от моделей с более высокой точностью, здесь каждый канал одновременно совмещает множество признаков, и никаких выраженных паттернов не наблюдается.

▍ Реализация на микроконтроллере

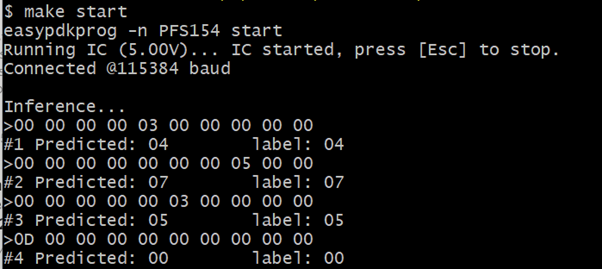
В первой итерации я использовал чуть более крупный экземпляр Padauk, PFS154. Он оснащён вдвое бо́льшим объёмом ROM и RAM, а также допускает перепрошивку, что сильно упрощает разработку ПО. С-версии кода инференса, включая отладочный вывод, сработали практически из коробки. Ниже вы видите прогнозы и метки, включая вывод последнего слоя.

А вот ужатие всего до размеров, подходящих для меньшего PMS150C, это отдельная история. Одной из существенных проблем при программировании этих устройств на С является то, что каждый вызов функции потребляет RAM для стека возврата и параметров функции. И это неизбежно, поскольку архитектура МК содержит всего один регистр (аккумулятор), в связи с чем все прочие операции должны происходить в RAM.

Чтобы эту проблему решить, я «сплюснул» код инференса и реализовал внутренний цикл на ассемблере, тем самым оптимизировав использование переменных. Ниже показан внутренний цикл, реализующий инференс из памяти в память для одного слоя. Двухбитный вес умножается на четырёхбитную активацию в аккумуляторе, после чего добавляется в 16-битовый регистр. Благодаря мощным возможностям архитектуры по манипулированию битами, для этого умножения требуется всего четыре инструкции (t0sn, sl, t0sn, neg). Расширяющее знак сложение (add, addc, sl, subc) также состоит из четырёх инструкций, демонстрируя ограничения 8-битных архитектур.

	void fc_innerloop_mem(uint8_t loops) {
 
    sum = 0;
    do  {
       weightChunk = *weightidx++;
__asm   
    idxm  a, _activations_idx
    inc _activations_idx+0
 
    t0sn _weightChunk, #6
    sl     a            ;    if (weightChunk & 0x40) in = in+in;
    t0sn _weightChunk, #7
    neg    a           ;     if (weightChunk & 0x80) in =-in;                    
 
    add    _sum+0,a
    addc   _sum+1
    sl     a 
    subc   _sum+1  
 
  ... 3x more ...
 
__endasm;
    } while (--loops);
 
    int8_t sum8 = ((uint16_t)sum)>>3; // Нормализация
    sum8 = sum8 < 0 ? 0 : sum8; // ReLU
    *output++ = sum8;
}

Как видно ниже, в итоге я смог втиснуть весь код инференса в тысячу килослов памяти и сократил потребление SRAM до 59 байт. (Заметьте, что вывод SDCC предполагает по 2 байта на слово инструкции при том, что содержит всего 13 бит).

Получилось! К сожалению, для вывода отладочной информации через UART не осталось свободной ROM. Тем не менее, исходя из верификации PFS154, я верю, что код работает, а поскольку у меня ещё нет в замыслах конкретного приложения, то и проект я решил оставить как есть.

▍ Обобщение

Реально можно реализовать инференс MNIST с хорошей точностью, используя один из самых дешёвых и простых микроконтроллеров на рынке. Значительный объём памяти и дополнительной обработки обычно уходит на реализацию гибких механизмов инференса, которые могут вместить широкий спектр операторов и структур моделей. Устранение этих издержек и сокращение функциональности до основной позволяет сильно упростить итоговое решение в этом супер эконом-сегменте.

Реализованный мной хак показывает, что поистине нет минимального предела применению машинного обучения и периферийных вычислений. Тем не менее возможность реализации полезных приложений на этом уровне весьма сомнительна.

Репозиторий проекта доступен на GitHub.