Введение
В данной статье пойдет речь о методе распознавания рукописного ввода путем математического анализа всех точек плоскости и перебора всех возможных комбинаций с целью отыскать наиболее лучшее наложение контрольных точек на ранее описанные фигуры. Поясню.
Рукописный ввод — это рисование мыслимым «пером» определенной фигуры. Рисование в компьютерных системах — это сохранение в графической памяти информации обо всех пикселях графического контекста. «Точка на плоскости» в математике — понятие абстрактное. В компьютерной же графике за этим понятием скрывается «пиксель». Данный алгоритм распознавания будет анализировать предоставленный ему набор точек( пикселей ) и пытаться в нем отыскать наиболее возможную и похожую фигуру. Фигура, в свою очередь, это каркас, содержащий лишь основные( контрольные ) точки, делающие фигуру уникальной.
Матчасть
Вообще говоря, сердце алгоритма — всем известная со времен школы Теорема Косинусов, являющаяся обобщенной теоремой Пифагора. Зная координаты трех точек плоскости и их порядок «появления» на ней, мы можем с легкостью определить угол, описанный этими точками( Вершина угла — вторая по счету точка ):
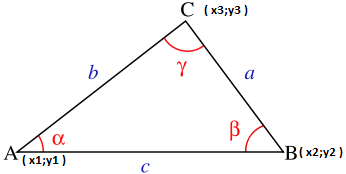
A( x1;y1 )
B( x2;y2 )
C( x3;y3 )расстояния между точками находятся по теореме Пифагора
a^ = b^ + c^ — 2*b*c*cos(ALPHA)
cos(BETA) = (b^+c^-a^) / 2*b*c
Зная косинус, величину угла легко можно вычислить.
Среди набора точек, которые подаются на вход алгоритма, необходимо «подставить» точки во всевозможные каркасы фигур( о них выше ) и выбрать наилучшее решение среди найденных. Делается это следующим образом:
- Мы берем первую и последнюю точки каркасов фигур. Уже две есть, осталось отыскать третью ( для нахождения величины угла ).
- Поиск третьей осуществляется перебором все последующих точек после первой. Решение включать точку в предполагаемый каркас фигуры принимается на основе двух анализов:
- Попытка подставить точку в угол( в качестве третьей, заключительной ) и проверить его на соответствие величине того же угла в каркасе реальной фигуры.
- Проверить отношение сторон получившегося угла с тем же отношением сторон угла в каркасе реальной фигуры.
Если эти два условия выполняются, то алгоритм принимает решение о включении точки из набора точек в мыслимый каркас( при этом увеличиваем величину похожести на текущую анализируемую фигуру ).
Если, допустим, у нас есть несколько анализируемых каркасов, например, «8» и «6». И результат алгоритма распознавания: «8»-80%, «6» — 90%, то решение принимается в пользу той фигуры, в каркасе которой присутствует больше контрольных точек, т.е в пользу восьмерки.
Процент сходства набора точек с точками в каркасе высчитывается просто: суммируются все точки, которые сошлись с теми же точками в каркасе и находится отношение. Допустим, если в каркасе N контрольных точек, а у нас сошлось M, то процент сходства —
M / N * 100
На словах что-то может быть непонятно. Поэтому вот все то же самое, но наглядно( на примере цифры «6» ):
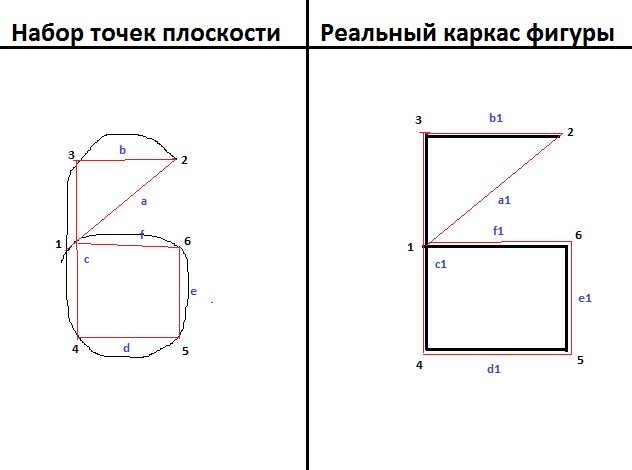
Черным обозначены наборы точек, красным — каркас, в соответствие с которым происходит анализ.
Цифрами обозначены точки углов( начиная с последнего ), если предполагать, что шестерку мы рисуем с точки «2» и заканчиваем точкой «1», то первые две точки, с которых начинается анализ каркаса — «1» и «2», затем происходит поиск точки «3», так, чтобы ее параметры относительно образуемого ею угла совпадали с теме же параметрами в каркасе. Далее, как мы нашли точку «3», ищем точку «4»( уже опираясь на точки «2» и «3» ) опять же, в соответствие с реальным каркасом и т.д.
Буквами обозначены стороны углов. Т.е, следуя правилам алгоритма, точка из набора( точек плоскости ) может быть включена в предполагаемый каркас, если( примеры ):
(угол 2 ~= углу 2 в каркасе) И ( a/b ~= a1/b1 ) то точка «3» будет включена
(угол 3 ~= углу 3 в каркасе) И ( b/c ~= b1/c1 ) то точка «4» будет включена
и т.д
Описание алгоритма на этом заканчивается.
Код
Легко сказать, но перед тем, как сказать нужно хорошо подумать, как сделать сказанное...
Что же, я уже подумал и реализовал придуманный алгоритм с помощью C++ и графической библиотеки OpenGL (+ надстройка GLUT). Графическая библиотека используется для рисования набора точек в двумерном пространстве. Кода получилось не так уж и мало, но и не так уж и много. Практически весь код разнесен по заголовочным файлам C++. Проект выложен в публичный доступ для всех, кому это хоть немножечко интересно. Исходники расположены на Bitbucket здесь. Проект использует систему контроля версий GIT, так что, у тех, кто пожелает выкачать исходные коды проекта, трудностей с этим возникнуть не должно.
Для перехода в режим программирования фигур нужно нажать в главном окне правой клавишей мыши. Затем нарисовать каркас( используя точки, соединенные между собою попорядку отрезками) и нажать среднюю кнопку мыши. На экране появится «Done!». После этого перезапустить приложение.
Подводные камни
Почти везде они есть… и этот алгоритм — не исключение. Прямо скажу, что алгоритм допускает периодические осечки в корректном распознавании.
Взять, к примеру, символы «S» и «5», где осечки практически неизбежны. Хотя, если качественно обозначить все контрольные точки, то, скорее всего, осечек удастся избежать. Также могут возникать осечки при анализе фигур, которые имеют сложные округлости. Если осечки происходят на непохожих символах( у меня, например, была осечка с «6» и «8»: 6 — 100%, 8 — 83% ), то можно запрограммировать каркас каждой из фигур повторно( количество повторений не ограничено ). Так удастся избежать ошибок в распознавании. И последнее, что нужно отметить — угол, образованный последней, первой и второй точками + соотношение его сторон нужно помнить. Для этого можно этот угол «выравнивать» до 90 градусов, как показано в демо ролике ниже.
В статье я упоминал лишь числа, как вы могли заметить. Но, на самом деле, распознавание применимо к абсолютно любым фигурам двумерного пространства. Я сделал небольшое приложение к статье — видео, демонстрирующее работу алгоритма.
Если у вас будут какие-либо вопросы, то задавайте — я с радостью на них отвечу.
Автор: Asen