Однажды, выполнив в Гугле запрос "Three body problem" ("Задача трёх тел"), я был просто поражен - первая страница результатов состояла только из ссылок на роман китайского писателя-фантаста Лю Цысиня с соответствующим названием, а также на телесериал, снятый по этому роману, т.е. собственно ссылок на задачу трёх тел не было вообще! Мне это показалось удивительным и несправедливым, поскольку сама по себе задача трёх тел тоже может выглядеть увлекательной в популярном изложении. В этой публикации я постарался привести некоторые доказательства этого утверждения.
Постановка задачи и её разновидности
Итак, задача трёх тел состоит в определении траекторий движения трех массивных тел, которые притягиваются в соответствии с Законом всемирного тяготения с силой, прямо пропорциональной массам тел и обратно пропорциональной квадрату расстояния между ними (эта сила центральная, т.е. действует в направлении центров массы тел). Для решения конкретной задачи начальные положения и скорости трех тел должны быть предварительно заданы. На самом деле аналогичные задачи могут возникать и для других видов взаимодействия, например, для заряженных частиц, притягивающихся или отталкивающихся по закону Кулона, но при гравитационном взаимодействии существует только притяжение (хотя я здесь иногда с благоговейным изумлением читаю статьи про устройство Вселенной и темную материю, поэтому готов поверить, что, возможно, и отталкивание тоже может происходить). В любом случае, наблюдение за гравитационным взаимодействие проще, чем исследование заряженных частиц. В трехмерном пространстве движение трёх тел описывается тремя координатами и тремя скоростями на каждое тело, запись уравнений движения для Закона всемирного тяготения приводит к системе 18-ти дифференциальных уравнений, связывающих координаты, скорости и ускорения тел. Этот случай образует полную задачу трёх тел. Существуют также важные частные случаи. В начальный момент три тела определяют плоскость в трехмерном пространстве, если начальные скорости таковы, что не содержат составляющих, направленных перпендикулярно этой плоскости, то и далее тела будут перемещаться в пределах первоначальной плоскости. Этот случай называется плоской задачей трех тел (Planar 3 Body Problem, P3BP), для его описания достаточно 12-ти дифференциальных уравнений. Наконец, если масса одного из тел намного меньше масс двух других, а движение происходит в одной плоскости, говорят о плоской ограниченной задаче трех тел (Planar Restricted 3 Body Problem, PR3BP), она описывается всего четырьмя дифференциальными уравнениями для двух координат и двух компонент скорости меньшего тела. Существует еще один частный, но очень важный вариант ограниченной задачи - круговая ограниченная задача (Circular Restricted 3 Body Problem, CR3BP), в которой рассматривается система, где наименьшее тело с пренебрежимо малой массой испытывает гравитационное воздействие двух других тел, меньшее из которых вращается вокруг большего по круговой орбите, при этом траектория наименьшего тела (космического корабля) НЕ ЛЕЖИТ в той же плоскости, в которой происходит вращение меньшего тела вокруг большего. В этом случае для описания движения космического корабля потребуется 6 дифференциальных уравнений - по одному для каждой из трех координат тела и по одному для для каждой из трех компонент скорости тела. Общая система уравнений для задачи трех тел в векторной форме выглядит так:
где - радиус-вектора трёх точек (центров массы тел),
- массы трёх тел,
- гравитационная постоянная.
Избавимся сразу от лишних деталей. Будем считать массой произведение истинной массы на гравитационную постоянную, также, поскольку решение уравнений зависит не собственно от масс, а от их отношений, разделим все массы на наибольшую (или наименьшую), в результате массы будут относительно небольшими числами. Я приведу здесь уравнения для разных видов задачи трёх тел в текстовом виде. Далее в некоторых случаях будут указываться начальные условия, это позволит каждому скопировать и внести уравнения и начальные условия в свою любимую программу для решения дифференциальных уравнений и воспроизвести картинки из этой публикации.
Полная задача трёх тел
(X1,Y1,Z1), (X2,Y2,Z2), (X3,Y3,Z3) - трехмерные координаты трёх тел
m1,m2,m3 - массы тел
У меня не нашлось интересных примеров применения полной задачи трёх тел,
а уравнения для неё выглядят достаточно громоздко, поэтому я их пока приводить не буду.
Но, если понадобится, я их сюда вставлю. Уравнения для частных видов задачи я привожу.
Плоская задача трёх тел
(X1,Y1), (X2,Y2), (X3,Y3) - плоские координаты трёх тел
m1,m2,m3 - массы тел
X1' = VX1
X2' = VX2
X3' = VX3
Y1' = VY1
Y2' = VY2
Y3' = VY3
VX1' = m2*(X2-X1)/((X1-X2)^2+(Y1-Y2)^2)^1.5+m3*(X3-X1)/((X1-X3)^2+(Y1-Y3)^2)^1.5
VX2' = m3*(X3-X2)/((X2-X3)^2+(Y2-Y3)^2)^1.5+m1*(X1-X2)/((X2-X1)^2+(Y2-Y1)^2)^1.5
VX3' = m1*(X1-X3)/((X3-X1)^2+(Y3-Y1)^2)^1.5+m2*(X2-X3)/((X3-X2)^2+(Y3-Y2)^2)^1.5
VY1' = m2*(Y2-Y1)/((X1-X2)^2+(Y1-Y2)^2)^1.5+m3*(Y3-Y1)/((X1-X3)^2+(Y1-Y3)^2)^1.5
VY2' = m3*(Y3-Y2)/((X2-X3)^2+(Y2-Y3)^2)^1.5+m1*(Y1-Y2)/((X2-X1)^2+(Y2-Y1)^2)^1.5
VY3' = m1*(Y1-Y3)/((X3-X1)^2+(Y3-Y1)^2)^1.5+m3*(Y2-Y3)/((X3-X2)^2+(Y3-Y2)^2)^1.5
Ограниченная задача трёх тел
(X,Y) - координаты тела с пренебрежимо малой массой (космического корабля)
m1,m2 - массы тел
X' = VX
Y' = VY
VX' = X+2*Y4-m1*(X+m2)/((X+m2)^2+Y^2)^1.5-m2*(X-m1)/((X-m1)^2+Y^2)^1.5
VY' = Y-2*Y3-m1*Y/((X+m2)^2+Y^2)^1.5-m2*Y/((X-m1)^2+Y^2)^1.5
Круговая ограниченная задача трёх тел
(X,Y,Z) - координаты тела с пренебрежимо малой массой (космического корабля)
mu - отношение массы меньшего тела (которое вращается вокруг большего) к сумме масс меньшего и большего
X' = VX
Y' = VY
z' = VZ
VX' = 2*VY+X-(1-mu) * (X+mu)/((X+mu)^2+Y^2+Z^2)^1.5-mu * (X-1+mu)/((X-1+mu)^2+Y^2+Z^2)^1.5
VY' = -2*VX+Y-(1-mu) * Y/((X+mu)^2+Y^2+Z^2)^1.5-mu * Y/((X-1+mu)^2+Y^2+Z^2)^1.5
VZ' = -(1-mu) * Z/((X+mu)^2+Y^2+Z^2)^1.5-mu * Z/((X-1+mu)^2+Y^2+Z^2)^1.5
Первые попытки решения задачи трех тел, случаи Эйлера и Лагранжа
Исторически первыми решениями задачи трех тел были решения Эйлера и Лагранжа, найденные соответственно в 1767 и 1772 годах. В обоих случаях для решения использовались специально подобранные начальные условия. В случае Лагранжа тела изначально располагаются в вершинах равностороннего треугольника, скорости тоже необходимо подобрать согласованными. Специальная замена переменных позволяет свести задачу трех тел к трем задачам двух тел (то есть тела взаимодействуют попарно), причем решения двух из этих задач можно выразить через решение третьей задачи). Траекториями движения являются эллипсы, для случая равных масс они одинаковы и повернуты друг относительно друга на 120 градусов, в общем случае эллипсы имеют разные размеры и расположение. Во время движения тела постоянно образуют равносторонний треугольник, размеры и положение которого постоянно меняются. Не берусь выписать решения в аналитическом виде, но их можно найти численно
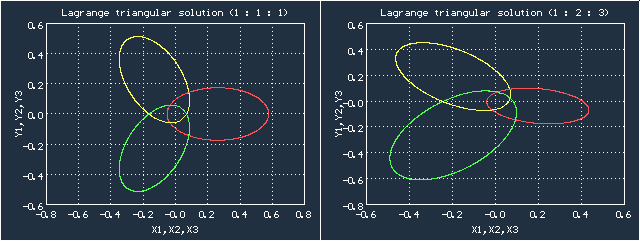
Анимированное движение тел для соотношения масс 1:2:3
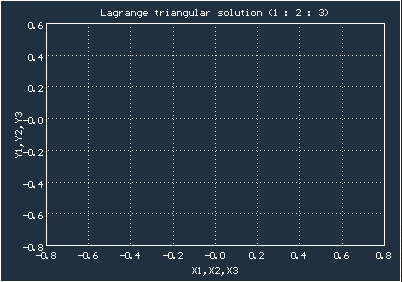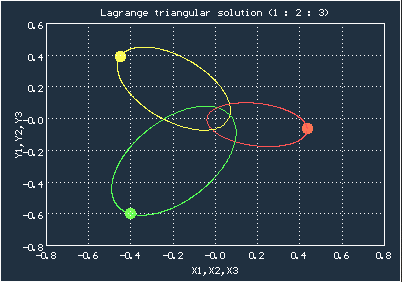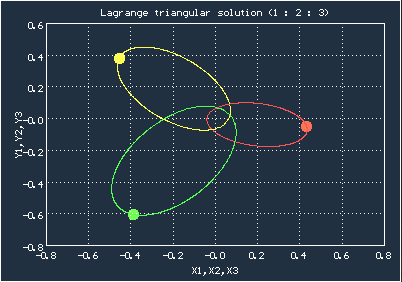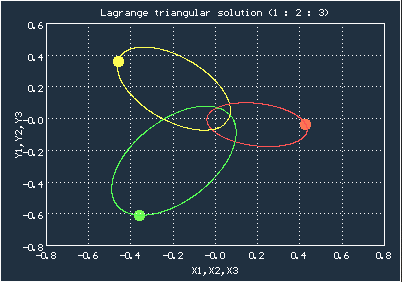
В случае Эйлера тела изначально располагаются на одной прямой (тоже не где попало, координаты и скорости должны быть согласованы), траекториями движения тоже служат эллипсы, а расположение на одной прямой во время движения сохраняется, но сама прямая изменяет своё положение.
Решения Эйлера и Лагранжа до сих пор остаются единственными известными точными решениями задачи трех тел. Они имеют не очень большое практическое значение, поскольку требуют очень точного задания начальных условий, которое трудно реализовать физически (точнее будет сказать, что решения неустойчивы, устойчивость они приобретают только в случае, когда масса одного из тел значительно меньше масс двух других).
Плоская задача трех тел, периодические траектории
В конце XIX века Анри Пуанкаре доказал существование бесконечного числа периодических решений ограниченной (плоской) задачи трех тел, а также методы продолжения этих решений на общую задачу трёх тел. С появлением и совершенствованием компьютеров исследователи стали обнаруживать все возрастающее количество плоских периодических траекторий для задачи трех тел, некоторые из этих траекторий выглядят довольно красиво. В этом разделе рассматриваются только случаи тел равной массы (она принимается равной 1).
Семейство Брука-Эно-Хаджидиметриу (1975)
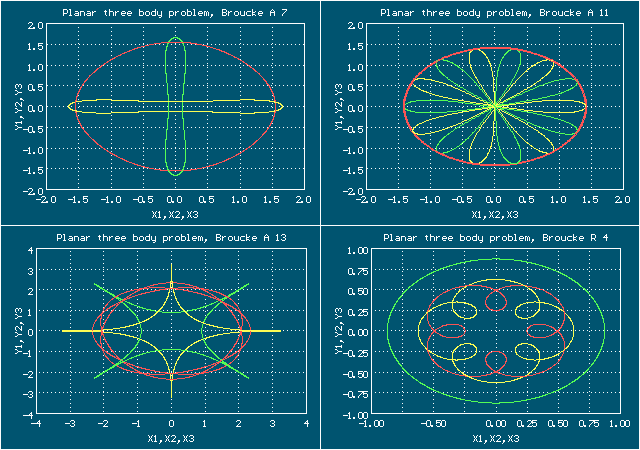
Анимированное изображение движения тел, орбита Брука, случай R 4
Здесь изображено два периода
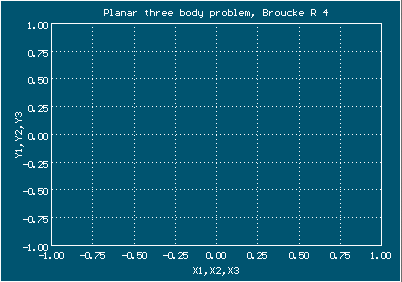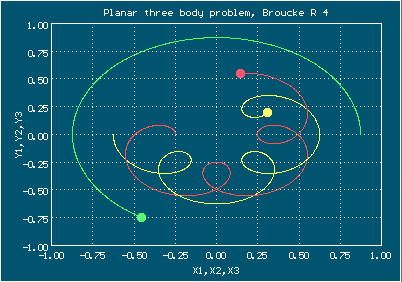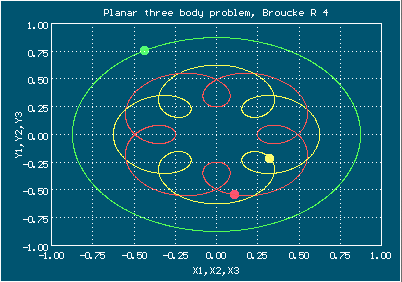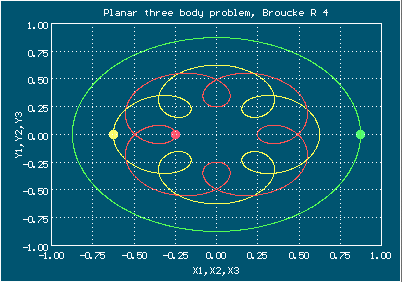
Начальные условия для орбиты Брука, случай R 4
T0 = 0, T1 = 5.4
X1(T0) = 0.8733047091
X2(T0) = -0.6254030288
X3(T0) = -0.2479016803
Y1(T0) = 0
Y2(T0) = 0
Y3(T0) = 0
VX1(T0) = 0
VX2(T0) = 0
VX3(T0) = 0
VY1(T0) = 1.010776444
VY2(T0) = -1.683353346
VY3(T0) = 0.6725769022
Семейство Шувакова-Дмитрашиновича (2013)
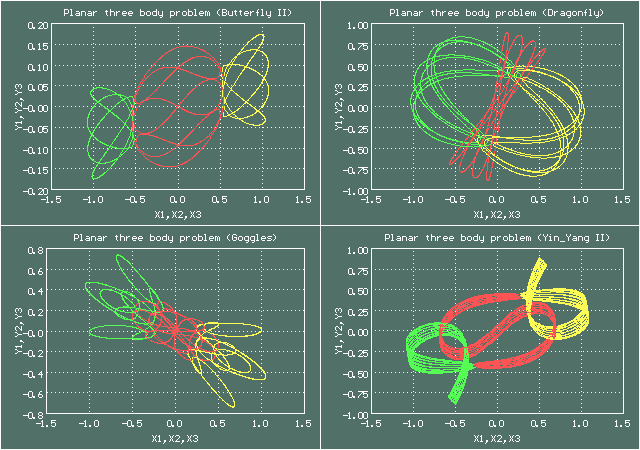
Анимированное изображение движения тел, орбита Шувакова-Дмитрашиновича (Dragonfly)
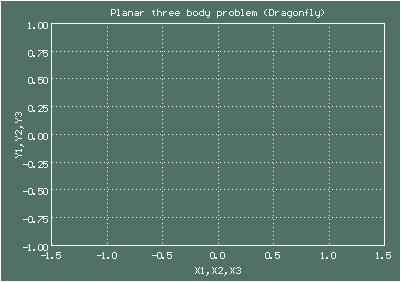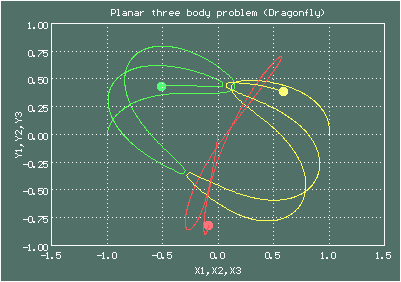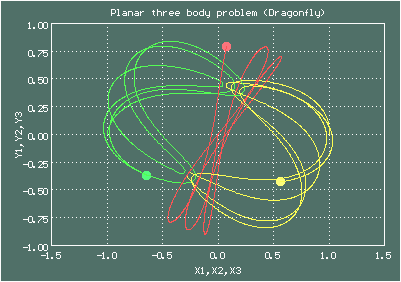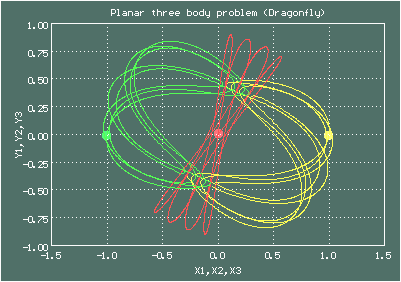
Начальные условия для орбиты Шувакова-Дмитрашиновича (Dragonfly)
T0 = 0, T1 = 22
X1(T0) = -1
X2(T0) = 1
X3(T0) = 0
Y1(T0) = 0
Y2(T0) = 0
Y3(T0) = 0
VX1(T0) = 0.08058
VX2(T0) = 0.08058
VX3(T0) = -0.16116
VY1(T0) = 0.58884
VY2(T0) = 0.58884
VY3(T0) = -1.17768
Орбиты Шувакова-Дмитрашиновича имеют довольно поэтические названия - Butterfly (Бабочка), Moth (Мотылёк), Dragonfly (Стрекоза), Goggles (Защитные очки), Yin-Yang (Инь-Ян), есть еще Bumblebee (Шмель) и Yarn (Пряжа)
Семейство Шина (Sheen 2016)
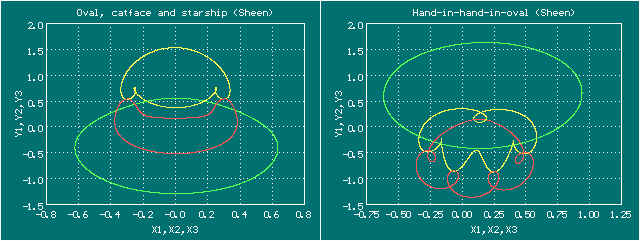
Анимированное изображение движения тел, орбита Шина (Овал, кошачья мордочка, космический корабль)
Здесь изображено два периода
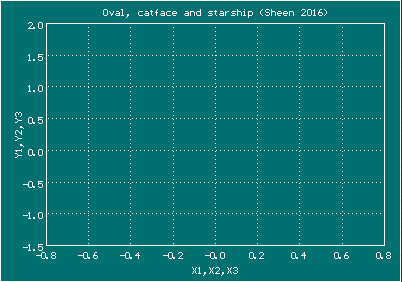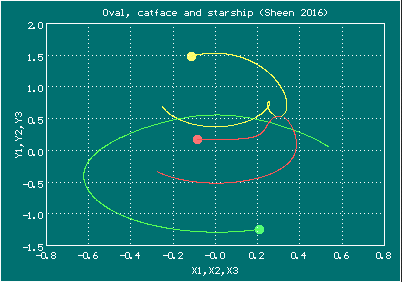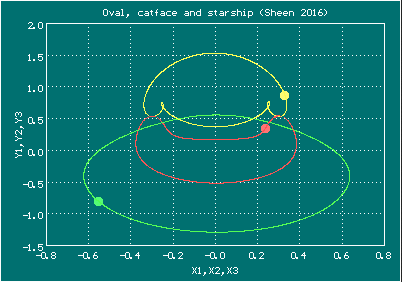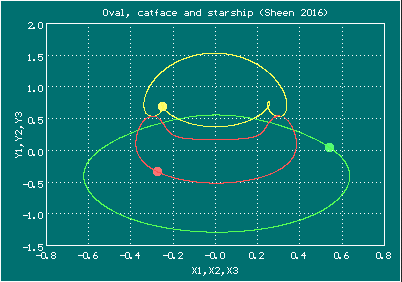
Начальные условия для орбиты Шина (Овал, кошачья мордочка, космический корабль)
T0 = 0, T1 = 5.1
X1(T0) = 0.5363870734
X2(T0) = -0.2520991265
X3(T0) = -0.2757066017
Y1(T0) = 0.05408860501
Y2(T0) = 0.6945273277
Y3(T0) = -0.3359335893
VX1(T0) = -0.5693795856
VX2(T0) = 0.07964461525
VX3(T0) = 0.4897349703
VY1(T0) = 1.255291103
VY2(T0) = -0.4586259973
VY3(T0) = -0.7966651052
Начальные условия для орбит из этого раздела взяты из Галереи орбит для плоской задачи трёх тел. Это прекрасный сайт, но анимации движения на нем даны в представлении на сфере, это полезно для понимания топологической структуры орбит, но иногда делает движение совершенно непонятным
Ограниченная задача трех тел, полеты к Луне
Ограниченная задача трех тел имеет более явное практическое значение, поскольку с её помощью можно описать движение космического корабля в космическом пространстве, в поле гравитационного воздействия небесных тел (в таких системах как Земля-Луна или Солнце-Земля). Первые попытки достижения космических тел с Земли вызвали необходимость решения задачи о траекториях, по которым должен перемещаться космический корабль, чтобы достигнуть Луны. Затруднительно перечислить имена всех исследователей, внесших свой вклад в построение орбит для реальных полетов к другим небесным телам, но среди первых следует упомянуть американца Ричарда Аренсторфа и советского ученого Всеволода Егорова. Основополагающая работа Егорова "О некоторых задачах динамики полета к Луне", вышедшая в 1957, содержала теоретическое решение вопроса о минимальных скоростях, необходимых для полета к Луне, решение задач о попадании в Луну и облёте Луны, также была рассмотрена задача о разгоне ракеты с помощью лунной гравитации (теперь это называется гравитационным маневром).
Среди прочего Егоров указал траектории, которые можно использовать для исследования Луны без постоянно работающего двигателя ракеты, только за счет гравитационного взаимодействии с Землей и Луной. Не вдаваясь в тонкости классификации траекторий полета к Луне, можно выделить два основных класса траекторий - периодические и непериодические. Периодические траектории, в свою очередь, бывают долётными и облётными. Долётные траектории позволяют приблизится к Луне на относительно небольшое расстояние, взглянуть на неё, так сказать, одним глазком и вернуться в сферу действия притяжения Земли. Облётные траектории позволяют, облетев Луну, увидеть её обратную сторону, которая, как известно, с Земли не видна.
По-английски долётные траектории называются cislunar, а облётные - circumlunar. В этом разделе будут рассматриваться только траектории, лежащие в одной плоскости (coplanar по-английски), т.е. те, которые можно обозначить как coplanar cislunar и coplanar circumlunar.
Эта цитата из книги: Виктор Себехей, "Теория орбит" объясняет, почему важно исследовать периодические орбиты:
Пуанкаре в первом томе своих Мethodes Nouvelles рассматривает периодические орбиты как единственный путь в исследовании задачи трех тел и подчеркивает их важную роль. Если дано частное решение ограниченной задачи, то всегда можно найти периодическое решение (с периодом, который может быть очень большим) такое, что разница между двумя этими решениями будет сколь угодно малой для любого заданного отрезка времени. Весьма интересна интерпретация Шварцшильда по поводу высказывания Пуанкаре, данная им на языке фазового пространства. В произвольно близкой окрестности любой точки в фазовом пространстве имеется точка, представляющая периодическую орбиту. Иначе говоря, небольшие изменения любых начальных условий приводят к периодической орбите, в общем случае с весьма большим периодом. Как в своей первоначальной форме, так и в модифицированной предложение Пуанкаре сводится к использованию периодических орбит в качестве исходных орбит.
Пользуясь только численным решением системы дифференциальных уравнений для ограниченной задачи трех тел, а также некоторыми рецептами, указанными в работах Егорова и других исследователей, можно самостоятельно построить некоторые периодические траектории, подходящие для исследования Луны. Эти рецепты таковы - нужно начинать с наиболее близкой к Луне точки траектории (она же наиболее удаленная от Земли), задавая её координаты, а также скорость ракеты в этой точке, для нахождения траекторий, симметричных относительно прямой, соединяющих центры Земли и Луны, достаточно задавать (и понемногу изменять) ту компоненту скорости ракеты, которая перпендикулярна этой прямой (можно считать, что это вертикальная компонента). Естественно, что начальная точка траектории должна лежать на вышеупомянутой прямой. Наконец, еще один рецепт - периодические траектории будут тем более устойчивыми (т.е. меньше зависеть от начальных данных), чем дальше от Луны будет находиться начальная точка (хотя этот рецепт противоречит требованию удобства наблюдения за лунной поверхностью).
Между прочим, судьба Всеволода Егорова, кажется, была загадочной и таинственной - как утверждает Википедия, он "6 сентября 2001 года пропал без вести в городе Сочи, где имел собственное жильё", это вполне в духе событий романа "Задача трех тел".
Описание траекторий в системе Земля-Луна формально относится к круговой
ограниченной задаче трех тел, поскольку орбита, по которой Луна вращается вокруг
Земли, довольно близка к окружности, но фактически для его описания достаточно обычной ограниченной задачи. Оказывается, что для описания движения в поле тяготения Земли и Луны удобно использовать разные системы координат. Наиболее просто движение выглядит в системе координат, которая вращается вместе с Луной, т.е. в которой Луна неподвижна относительно Земли (такая система называется синодической). Это всегда можно сделать, поскольку сила гравитационного взаимодействия зависит не от конкретного положения тел, а только от расстояния между ними. Более сложной, но и более реалистичной выглядит сидерическая система координат, в которой движение рассматривается относительно неподвижных звезд. В этой системе Луна вращается вокруг Земли по (примерно) окружности с периодом, равным сидерическому месяцу (приблизительно 27 суток 8 часов), в течение которого Луна совершает полный оборот вокруг Земли. В дальнейшем здесь в основном будет рассматриваться движение в синодической системе, кроме нескольких специальных случаев, для которых явно будет отмечено использование сидерической системы. Переход от синодических координат (в которых Луна неподвижна) к сидерическим (в которых Луна вращается вокруг Земли по круговой орбите) осуществляется по формулам:
Далее при построении периодических траекторий в системе Земля-Луна будут использоваться следующие соглашения: среднее расстояние от Земли до Луны (приблизительно 384000 км) будет принято за 1, произведение универсальной гравитационной постоянной G на массу Земли также считается равным 1, поэтому то же произведение для Луны приблизительно равно 1/81.45 (примерно 0.01227747). Вообще, не очень понимаю, как определяют массу космических тел, предполагаю, что как раз через наблюдение за их движением и взаимодействием, т.е. с помощью обратного применения Закона всемирного тяготения. Земля находится в точке (0,0), а Луна - в точке (1,0).
Следующие несколько траекторий для системы Земля-Луна мне удалось построить самостоятельно. Разумеется, все они были давно известны, но в работах по этой тематике не всегда приводятся начальные условия для траекторий, да и просто интересно было самому отыскать их с помощью, по сути, игрушечной программы для графического исследования дифференциальных уравнений.
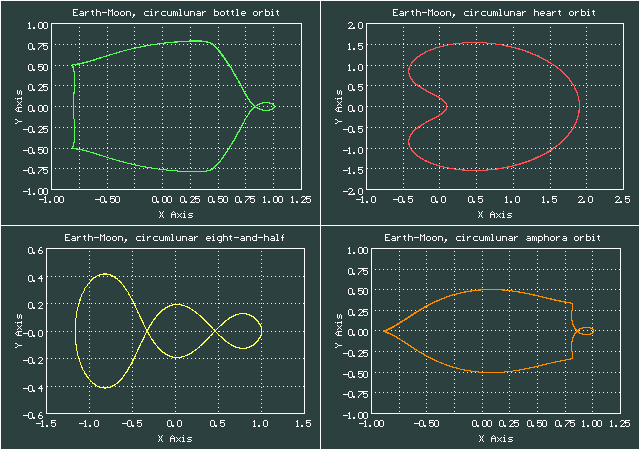
Названия для этих орбит ("бутылка", "сердце", "полторы восьмерки", "амфора") я тоже придумал сам, они не являются общепринятыми, я просто буду использовать их здесь для удобства
Анимация, изображающая процесс поиска периодической траектории для случая 'бутылки'
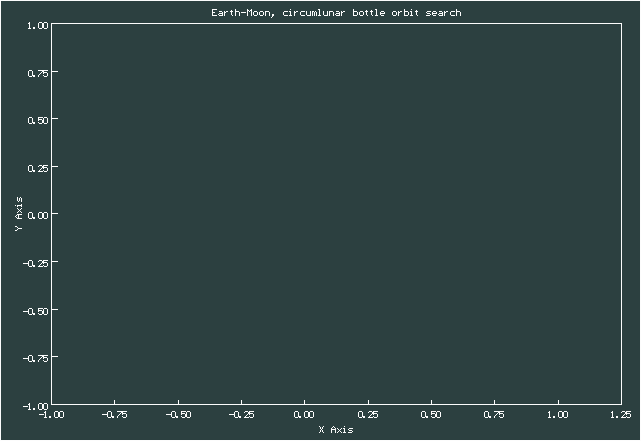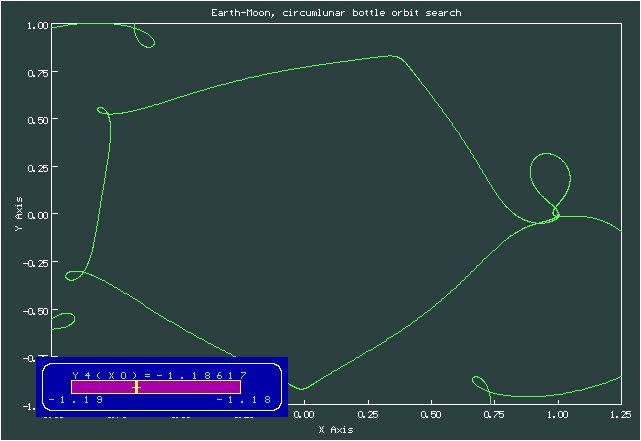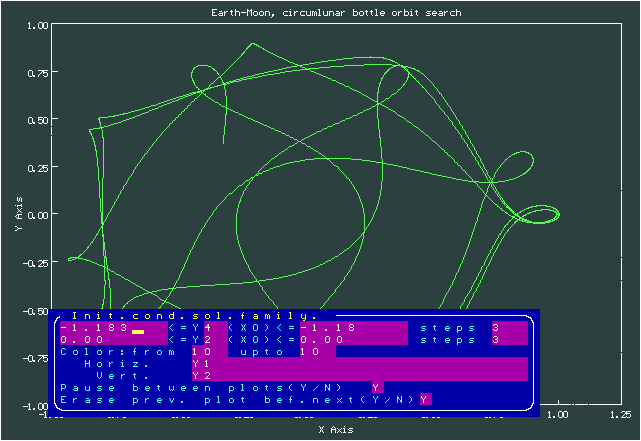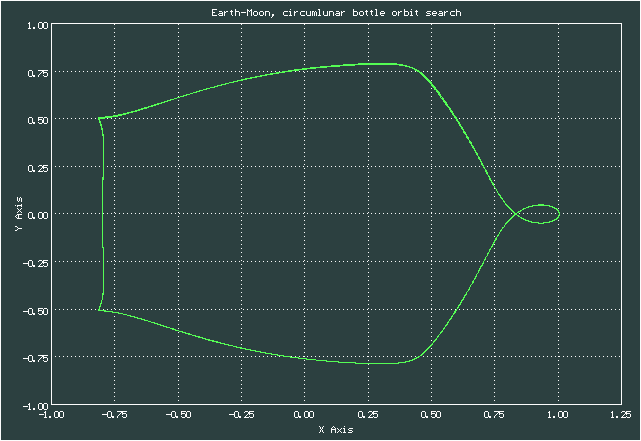
Начальные условия для случая 'бутылки'
T0 = 0, T1 = 70
X(T0) = 1.0045
Y(T0) = 0
VX(T0) = 0
VY(T0) = -1.18311976
Системные параметры (массы):
m1 = 0.987722529
m2 = 0.012277471
Другие интересные траектории, возникающие в системе Земля-Луна
Орбита Аренсторфа
Ричард Аренсторф открыл эту орбиту в 1963 году. Формой она немного напоминает "брецель" - своеобразный крендель родом из Германии. Здесь представлены два варианта этой орбиты - долётный (cislunar) и облётный (circumlunar). Начальные данные для долётного варианта взяты из книги: Хайрер Э., Нерсетт С., Ваннер Г. "Решение обыкновенных дифференциальных уравнений", а начальные данные для облётного варианта я подобрал сам
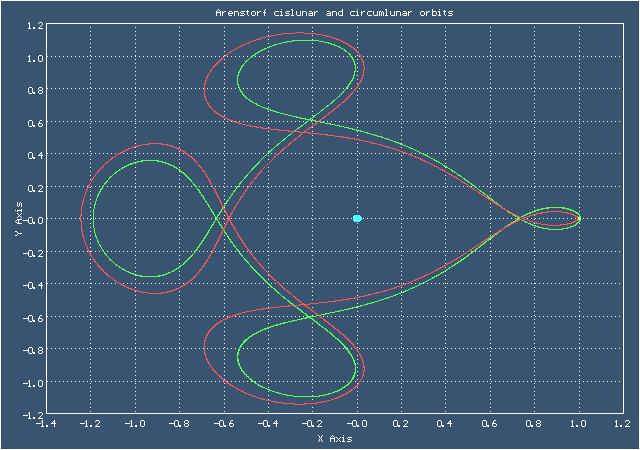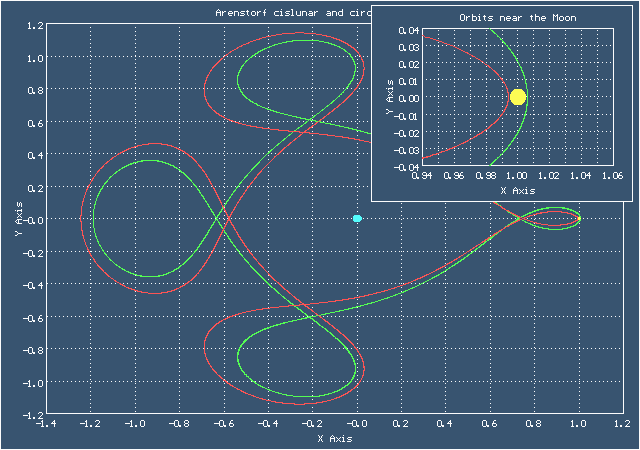
Анимированное изображение движения по долётной и облётной орбитам Аренсторфа
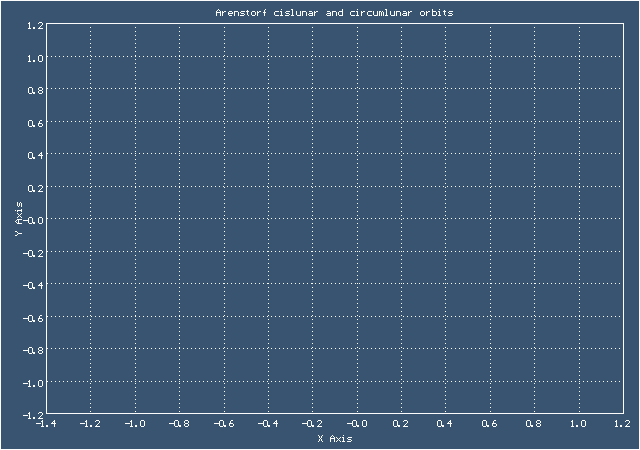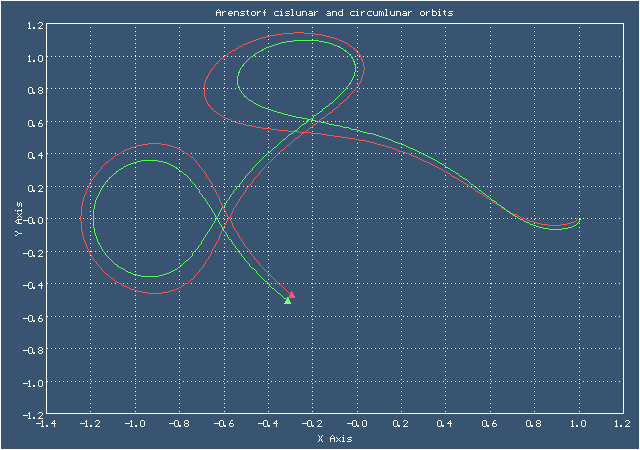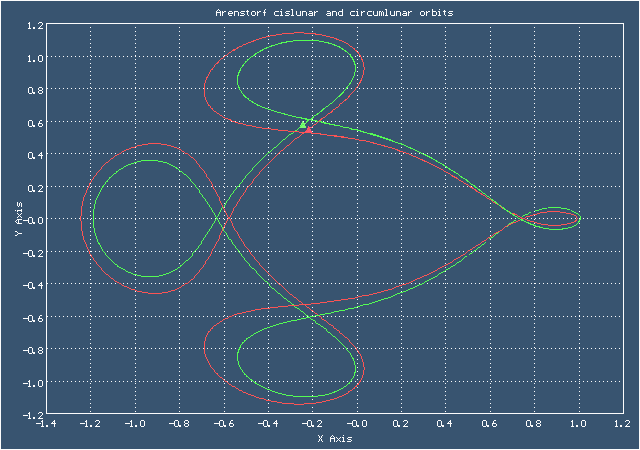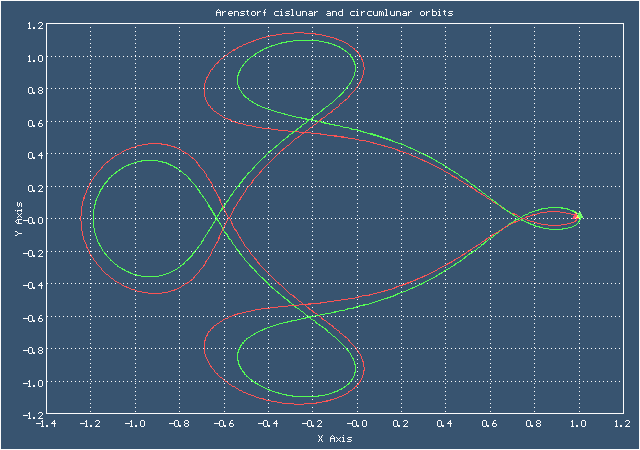
Начальные условия для орбит Аренсторфа
T0 = 0, T1 = 34.130434 (два периода)
долётная облётная
X(T0) = 0.994 1.006
Y(T0) = 0 0
VX(T0) = 0 0
VY(T0) =-2.001585106 -1.181158683
Системные параметры (массы тел):
m1 = 0.987722529
m2 = 0.012277471
Орбита Дэвидсона
Открыта в 1964 году. Эта орбита очень красивая, но очень же и неустойчивая, как пишет о таких орбитах Виктор Себехей в "Теории орбит",
неустойчивы почти во всех смыслах, действительно, их чувствительность к изменениям значения массового параметра (отношения массы Луны к массе Земли) такова, что в некоторых случаях переход от спутника Земли к спутнику Луны, и наоборот, может не произойти, если значение изменится на доли процента
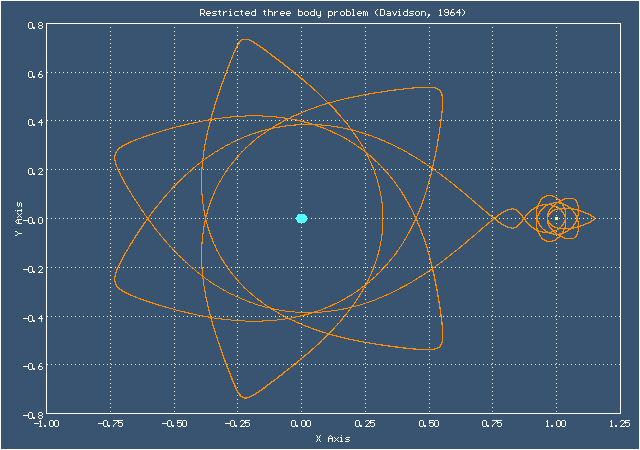
Анимированное изображение движения по орбите Дэвидсона
Здесь изображено два периода

Начальные условия для орбиты Дэвидсона
T0 = 0, T1 = 50
X(T0) = 1.15
Y(T0) = 0
VX(T0) = 0
VY(T0) = 0.0086882909
Системные параметры (массы):
m1 = 0.987722529
m2 = 1-m1
Интересно, что в "Теории орбит" приведены начальные условия для этой орбиты, но с ними построить её у меня не получилось, кое-что пришлось тоже подбирать самостоятельно (а именно - минимальное расстояние от Луны)
Траектория свободного возвращения, моделирование полета Аполлона-13
Траектория свободного возвращения для системы Земля-Луна - это траектория, которая позволяет космическому кораблю, запущенному к Луне, возвратиться на Землю без использования двигателей, только за счет гравитационного взаимодействия с Землей и Луной (под возвращением следует понимать либо посадку на Землю, либо перемещение в точку, расположенную достаточно близко от земной поверхности, из которой уже можно осуществить посадку с небольшими затратами энергии). По-английски такие траектории называются "free-return orbit" или "rescue orbit" (т.е. "орбита спасения"). Для перемещения по такой орбите космический корабль должен оказаться в определенной точке пространства, имея определенную скорость (точнее, определенные величину и направление скорости), далее перемещение к Земле может происходить с выключенным двигателем, т.е. без затрат энергии. Исследование таких траекторий началось еще до первых космических полетов, они рассматривались как средство для подстраховки при полете к Луне на случай какой-либо аварии, после которой использование двигателя космического аппарата будет невозможным или очень ограниченным. Как и прочие орбиты, траектории свободного возвращения бывают долётными (чтобы подлететь к Луне со стороны Земли поближе, а затем вернуться), а также облётными (предусматривающими облёт Луны). Такие орбиты могут иметь разную форму, наиболее известной является "восьмерка", две петли которой окружают Землю и Луну соответственно (для облётных траекторий) или одна из петель окружает Землю, а другая проходит близко от Луны (для долётных траекторий).
Первым космическим кораблем, осуществившим облёт Луны по траектории свободного возвращения, была советская автоматическая космическая станция "Луна-3", в октябре 1959 года передавшая на Землю первые фото обратной стороны Луны.Такие траектории также активно использовались в американской космической программе "Apollo", хотя обычно полеты происходили по комбинированной схеме - полет начинался с достижения какой-либо орбиты вокруг Земли, потом осуществлялся маневр (он назывался Trans-Lunar Injection - TLI), который позволял переместиться на орбиту свободного возвращения для полета к Луне, затем во время полета по этой орбите тестировались все системы корабля, если все было нормально - осуществлялся еще один маневр для перехода на орбиту, более удобную для исследования Луны (орбита свободного возвращения сильно ограничивает места, в которых космический аппарат может прилуниться).
Первыми людьми, увидевшими воочию обратную сторону Луны, был экипаж корабля"Apollo-8", но фактически его орбита тоже была комбинированной. Несмотря на это, реальная орбита "Apollo-8" не очень отличалась от орбиты свободного возвращения в виде "восьмерки", что и было увековечено в памятном медальоне, выпущенном по случаю предстоящего полета (интересно, что автором дизайна медальона был пилот командного модуля "Apollo-8" Джим Ловелл).

Единственным же кораблем программы "Apollo", который облетел Луну по орбите свободного возвращения, был "Apollo-13", и это стало следствием нештатной ситуации, возникшей на борту.
Американский пилотируемый космический корабль "Apollo-13" стартовал 11 апреля 1970 года с космодрома на мысе Кеннеди во Флориде. Экипаж состоял из того самого Джима Ловелла (теперь он был командиром корабля), а также Джона Свайгерта и Фрэда Хейза. Целью полёта была высадка человека на поверхность Луны и проведение научных исследований. Первые двое суток полёта проходили без каких-либо происшествий, но через 55 часов 54 минуты 53 секунды после старта произошел взрыв кислородного баллона и выход из строя двух из трех батарей топливных элементов, которые обеспечивали электропитание в отсеке экипажа командного модуля (он назывался "Odyssey"). Именно тогда Свайгерт произнёс, а Ловелл продублировал фразу "Хьюстон, у нас проблема". От высадки на Луну пришлось отказаться, а экипаж вынужден был бороться за сохранение своих жизней, обеспечивая возвращение на Землю и испытывая при этом большие неудобства от холода и недостатка кислорода. Командный модуль был поврежден взрывом, поэтому для обеспечения маневров пришлось использовать лунный модуль ("Aquarius"), ресурсы которого были крайне ограничены. Тем не менее экипажу удалось благополучно возвратиться на Землю. Драматические события этого полёта показаны в фильме "Apollo-13" с Томом Хэнксом в роли Ловелла.
Я попробовал построить модель траектории, по которой происходил полёт "Apollo-13". Скажу сразу, это очень грубая модель траектории свободного возвращения, кроме того, известно, что космический корабль не все время придерживался этой траектории (после инцидента произошло 4 её корректировки). Тем не менее основные параметры траектории примерно таковы, как указано в статье английской Википедии - минимальное расстояние до Луны, достигнутое в самой дальней точек траектории равно 254 км, использовалось также известное полное время полета, составлявшее без малого 6 суток.
Если в строке поиска Гугла указать "Arenstorf orbit" и осуществить поиск изображений, в большей части результатов будет изображена та самая орбита Аренсторфа в виде "брецеля", которая уже была рассмотрена здесь (или другая её разновидность, с тремя завитками вместо четырех). Однако также в статьях об Аренсторфе говорится о том, что он разработал "орбиту спасения", которая была использована для благополучного возвращения экипажа "Apollo-13" на Землю. Орбита-брецель явно не могла быть для этого использована, поскольку она проходит на довольно значительном расстоянии от Земли. Не могу утверждать наверняка, но для построения орбиты свободного возвращения могла быть использована другая орбита, первооткрывателем которой действительно был Аренсторф. Эта орбита периодическая, но траекторией свободного возвращения является не вся орбита целиком, а её часть (точнее, одна часть в начале периода вместе с одной частью в конце периода). Скромно упомяну, что эту траекторию я тоже сначала нашел сам, с помощью перебора вертикальной составляющей скорости вблизи Луны, а уже потом обнаружил её изображения в статьях соответствующей тематики. Она напоминает цветок с четырьмя лепестками.
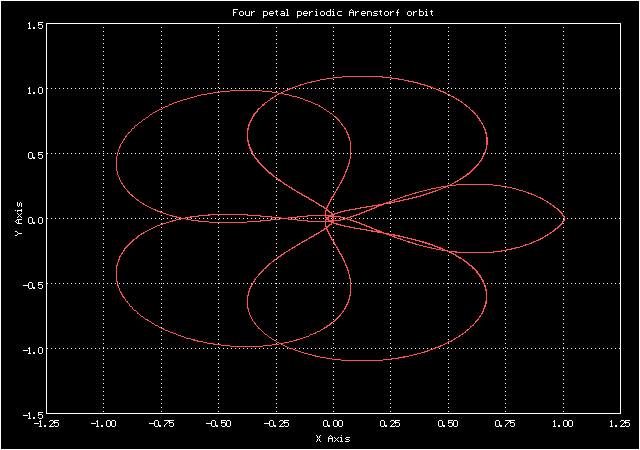
Анимированное изображение движения по четырёхлепестковой орбите Аренсторфа
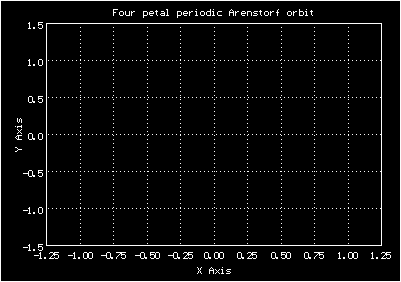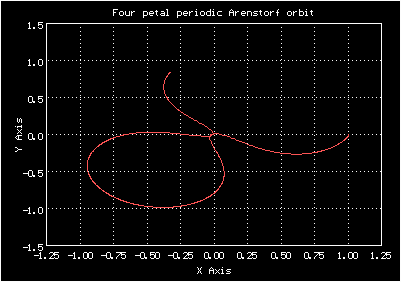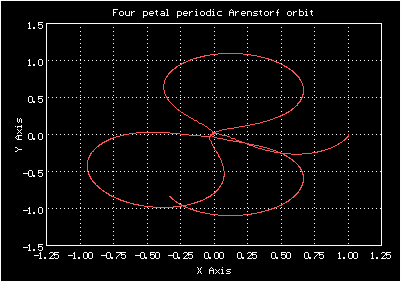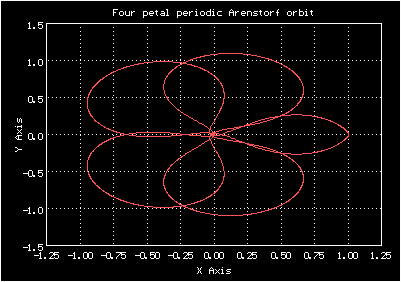
Начальные условия для четырёхлепестковой орбиты Аренсторфа
T0 = 0, T1 = 20
X(T0) = 1.00524
Y(T0) = 0
VX(T0) = 0
VY(T0) = -1.504550898
Системные параметры (относительные массы Земли и Луны):
m1 = 0.987722529
m2 = 0.012277471
Рассматривая анимацию для этой орбиты, нетрудно заметить, что её часть в конце периода вместе с другой частью в начале следующего периода как раз и образуют орбиту в виде "восьмерки" вокруг Земли и Луны.
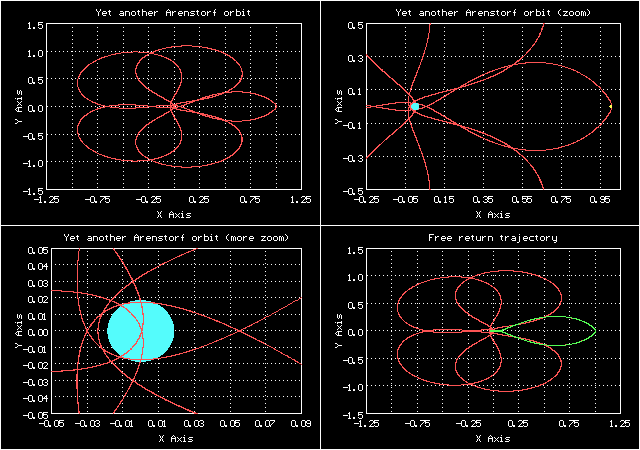
Так она выглядит в синодической системе координат (которая перемещается вместе
с Луной, т.е. в которой Луна неподвижна).
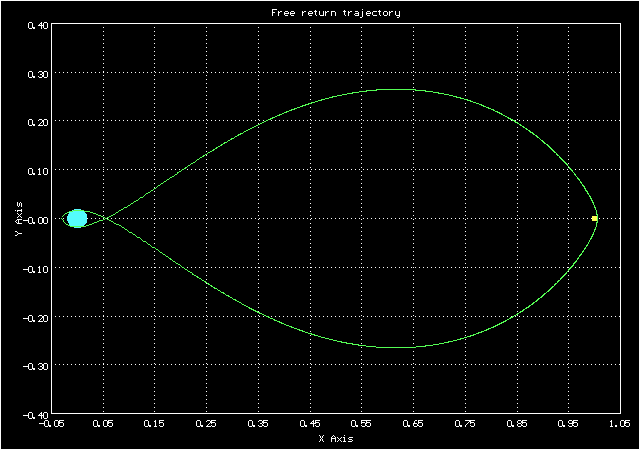
Анимированное изображение движения по траектории свободного возвращения в синодической системе координат
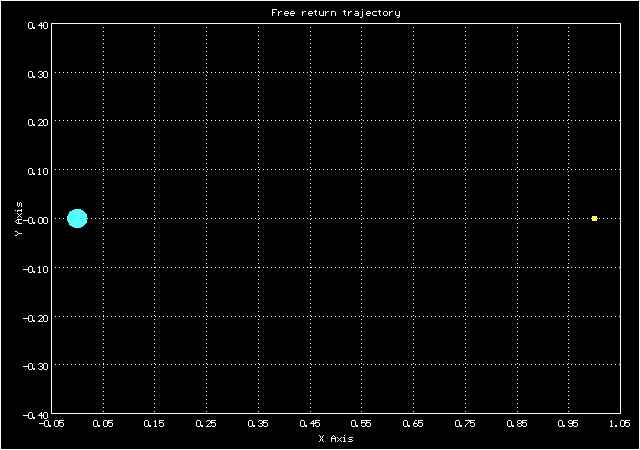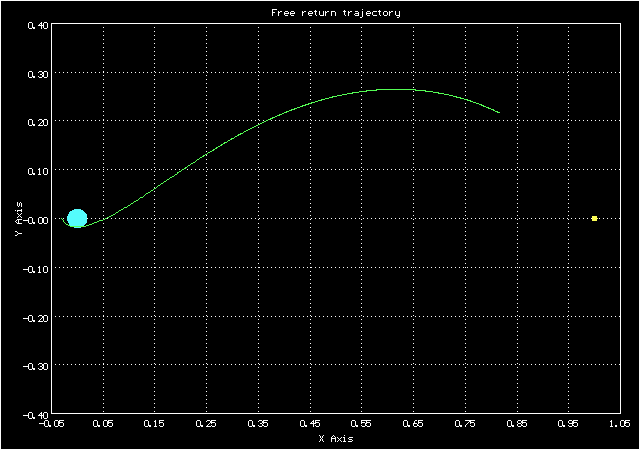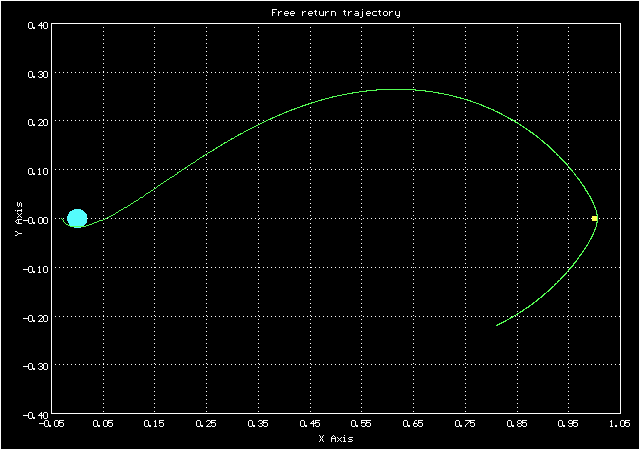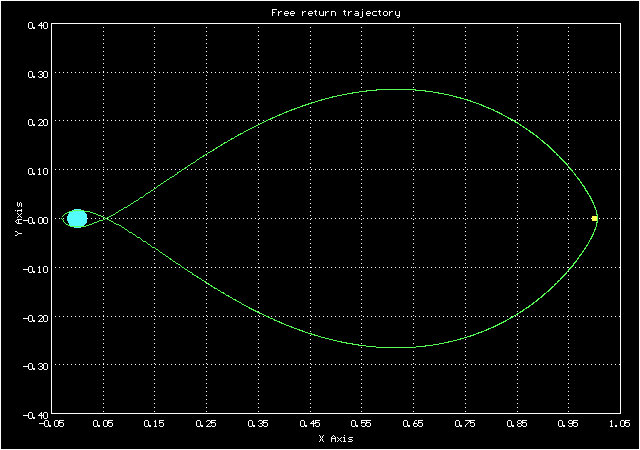
А такой вид у орбиты в сидерической системе координат
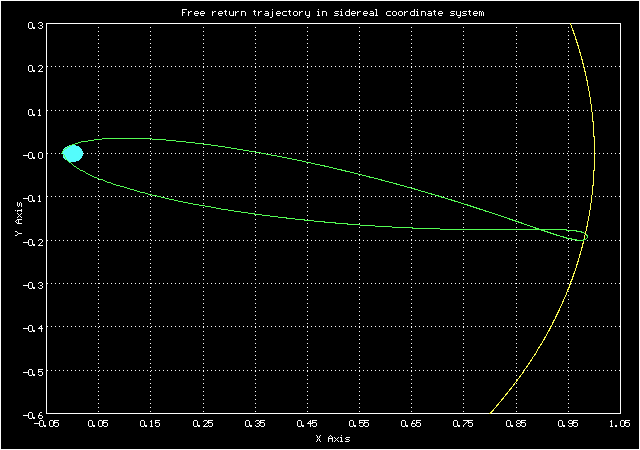
Анимированное изображение движения по траектории свободного возвращения в сидерической системе координат
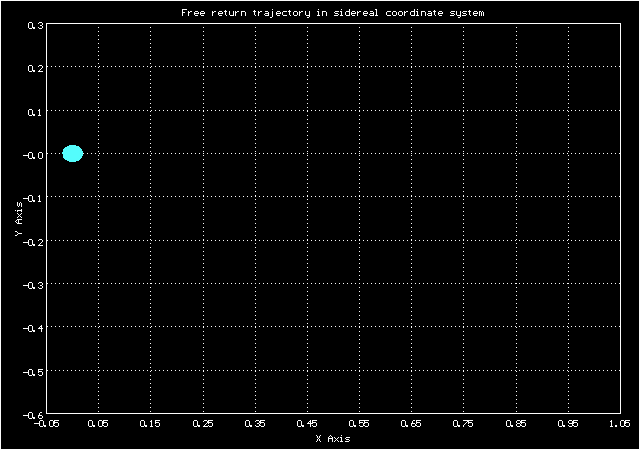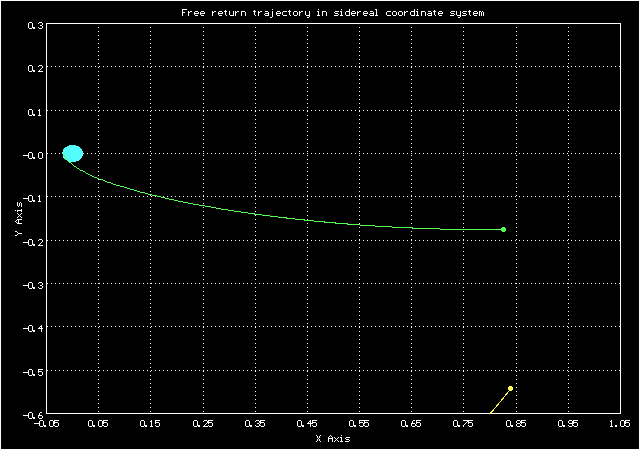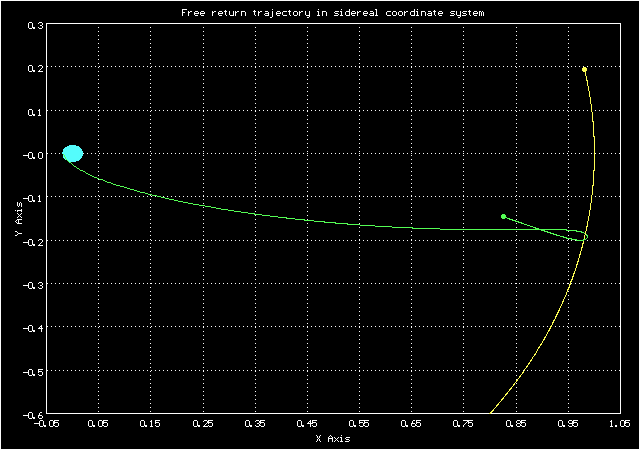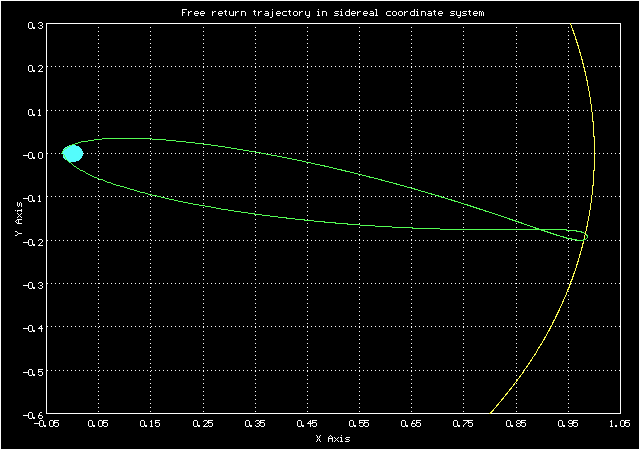
Видно, что она вполне похожа на изображение орбиты на экране в Центре Управления Полетом на кадре из фильма "Apollo-13"
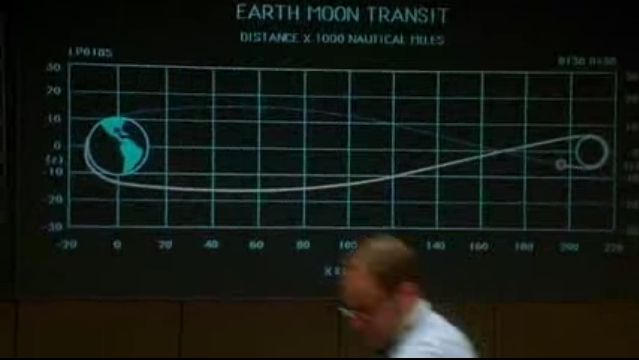
Начальные условия для орбиты свободного возвращения
T0 = 11.5482, T1 = 13.1985
X(T0) = -0.00793071912
Y(T0) = -0.01670249383
VX(T0) = 10.42031766
VY(T0) = -1.952404189
Системные параметры (относительные массы Земли и Луны):
m1 = 0.987722529
m2 = 0.012277471
Решение в сидерической системе получается с помощью преобразования
Xnew = X*cos(t)-Y*sin(t)
Ynew = X*sin(t)+Y*cos(t)
Разумеется, существует множество разных орбит свободного возвращения. Немного изменяя вертикальную скорость в начальной точке орбиты (напомню, для построения удобно считать, что она является ближайшей к Луне), можно получить орбиты, близкие к рассмотренной выше. Они уже не будут частью большой периодической орбиты, но, пользуясь свойством симметрии решений, можно их достроить до орбит, позволяющих облететь Луну и вернуться.
Виктор Себехей, "Теория Орбит" $8.6.3 - Свойство симметрии решений
В отношении выбора начальных условий для периодических орбит ... нужно сделать несколько дополнительных замечаний. Уравнения движения ограниченной задачи обладают тем свойством, что если
есть частное решение, то
тоже будет решением
Разные близкие орбиты свободного возвращения в окрестности Земли, вместе с периодической (зелёной)
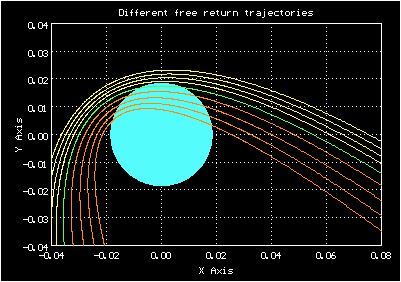
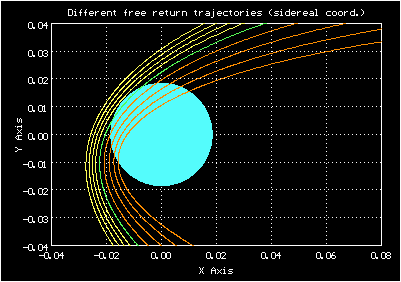
Движение происходит справа налево. Кажется, лучше возвращаться по оранжевым орбитам, по желтым можно улететь неизвестно куда
HALO и NRHO-орбиты, круговая ограниченная задача трех тел
HALO орбиты - это орбиты, связанные с точками Лагранжа в системах двух массивных тел. Их особенностью является то, что тело с пренебрежимо малой массой движется вокруг меньшего из массивных тел, причем движение происходит в плоскости, перпендикулярной той, в которой меньшее тело вращается вокруг большего. Название HALO (далее я попробую объяснить его происхождение) впервые употребил Роберт Фаркуар, который предложил использовать такую орбиту в качестве орбиты для ретранслятора, с которого все время видно как Землю, так и обратную сторону Луны. Ретранслятор был нужен для осуществления связи с участниками миссии Apollo, предполагалось, что космический корабль будет совершать посадку на обратной стороне Луны. В конце концов от идеи посадки на невидимой стороне Луны отказались (корабли Apollo садились на ту сторону Луны, которая обращена к Земле), но изучение таких орбит продолжилось и у них были обнаружены многочисленные полезные свойства, которые можно использовать для исследования Луны.
NRHO (Near Rectilinear Halo Orbit - Близкая к Прямолинейной HALO Орбита) - это подвид HALO орбит, они замечательны тем, что движение космического корабля на отдельных участках очень похоже на прямолинейное. Такие орбиты являются слегка неустойчивыми, но исправление этой неустойчивости требует не очень больших затрат энергии.
В качестве примера рассмотрим так называемую резонансную орбиту NRHO 9:2.
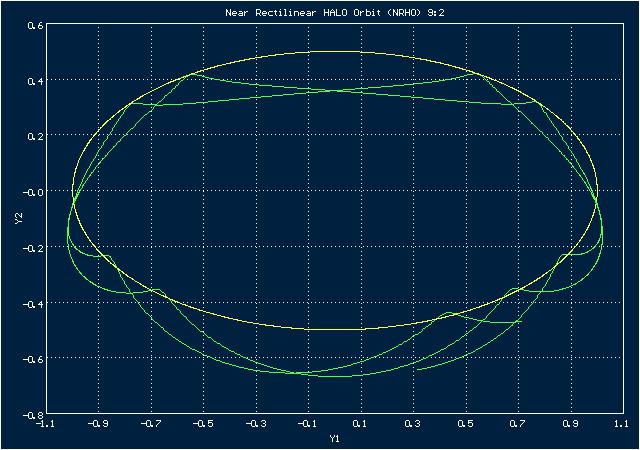
Анимированное изображение движения по орбите NRHO 9:2 в системе координат, в которой Земля неподвижна
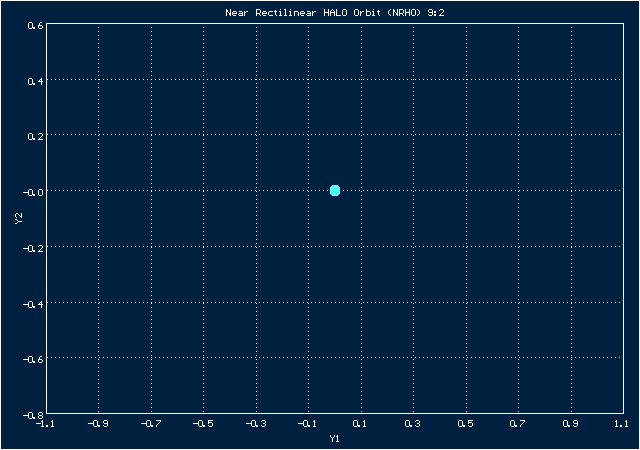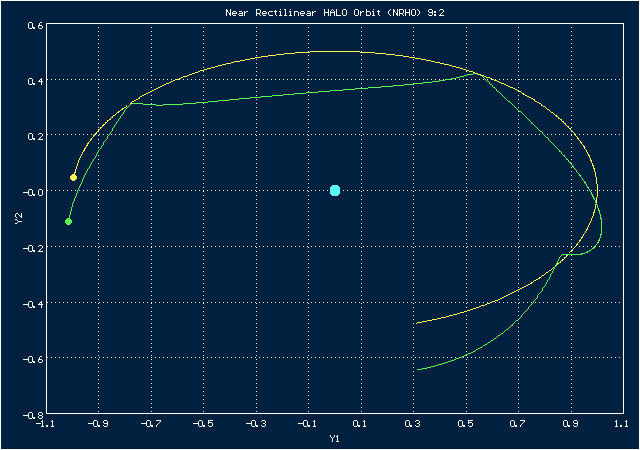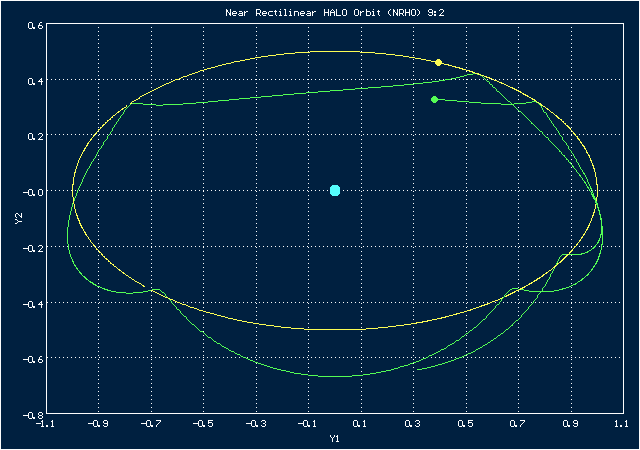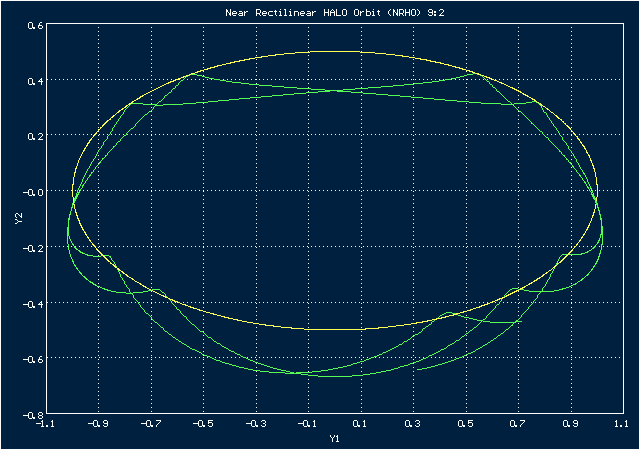
Эта орбита - квазипериодическая, а 9:2 означает, что 9 (почти)периодов (оборотов космического корабля вокруг Луны) этой орбиты приходятся на 2 периода (оборота) Земли вокруг Луны. Она связана с коллинеарной точкой Лагранжа , расположенной за Луною на прямой, соединяющей Луну с Землею. Если смотреть с Земли, орбита может проходить как перед орбитой Луны, так и за ней. Это означает, что в определенных точках космический корабль будет находится по ту сторону Луны, которая обращена к Земле, а в других точках он будет с той стороны Луны, которая не видна с Земли, обеспечивая для себя таким образом видимость обратной стороны Луны. Следует также добавить, что эту орбиту предполагается использовать в проекте Lunar Gateway, согласно которому по ней будет вращаться вокруг Луны многомодульная станция.
Чтобы лучше понимать устройство такой орбиты. можно как бы остановить движение, а потом рассмотреть трёхмерное изображение орбиты со всех сторон
Трёхмерное изображение орбиты NRHO 9:2 в системе координат, в которой Земля неподвижна
Здесь изображены два (почти)периода орбиты

Можно также попробовать рассмотреть изображение этой орбиты в координатной системе, в которой Земля и Луна неподвижны
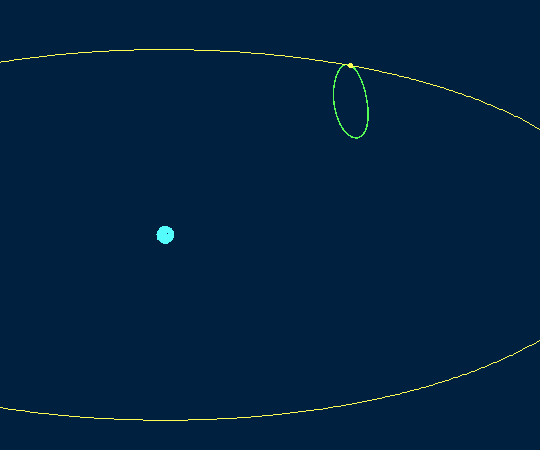
Это изображение помогает понять, почему HALO орбиты так называются - если смотреть на них с Земли, они напоминают лунное гало, оптическое явление, при котором возникает вторичное свечения вокруг источника света.
Трёхмерное изображение орбиты NRHO 9:2 в системе координат, в которой неподвижна Луна (и Земля тоже)
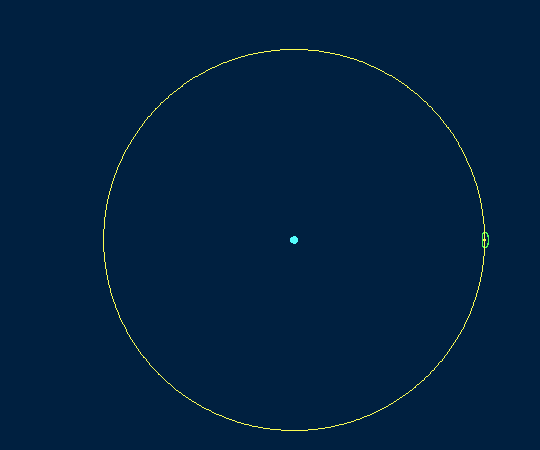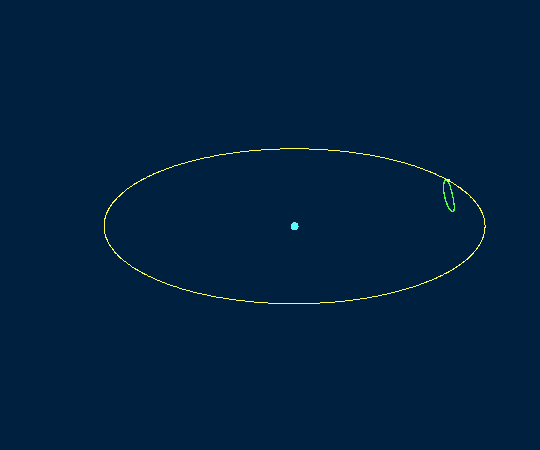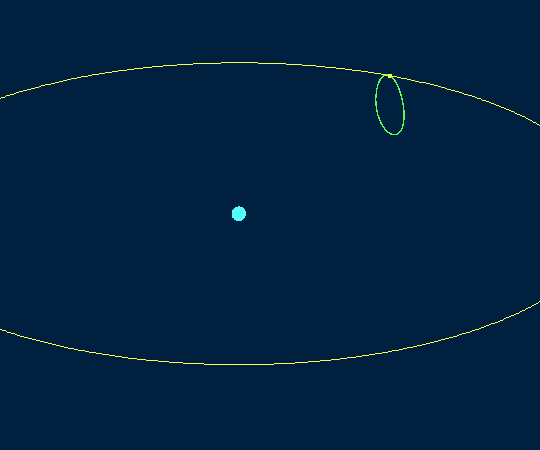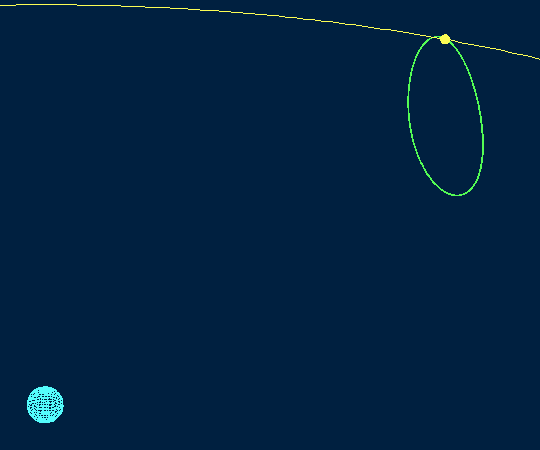
Здесь будет уместно привести начальные условия для орбиты NRHO 9:2
Начальные условия для орбиты NRHO 9:2
T0 = 0, T1 = 13 (чуть больше одного (почти)периода)
X(T0) = 1.021079744
Y(T0) = 0
Z(T0) = -0.18162
VX(T0) = 0
VY(T0) = -0.10176
VZ(T0) = 9.76561018E-7
Массовый параметр - отношение массы Луны к суммарной массе Земли и Луны:
mu = 0.012277471
Начальные условия взяты из диссертации
"Trajectory design and targeting for applications to the exploration program in cislunar space", автор Emily M. Zimovan Spreen. Нужно отметить, что и здесь пришлось немного подгонять эти условия, чтобы всё работало как следует. Подозреваю, что дело в значении массового параметра, автор может пользоваться значением, которое несколько отличается от используемого мною (хотя в диссертации я этого значения просто не нашёл). В любом случае принципиально это дела не меняет.
Заключение
В заключение хочу извинится за возможные ошибки и неточности. В своё оправдание могу сказать, что космосом я никогда не занимался, космонавтом в детстве быть не мечтал, высоты вообще боюсь. Тем не менее мне интересно было попробовать изучить вопросы освоения космоса с такой чисто теоретической точки зрения (с помощью численного решения дифференциальных уравнений для задачи трёх тел), и рассмотреть результаты именно в виде изображений. При этом не перестаю удивляться необыкновенным красоте и разнообразию решений задачи трёх тел.
И ещё
Вынужден также сознаться, что роман "Задача трёх тел" я не читал, и сериал по роману тоже не смотрел - не очень люблю любую фантастическую литературу. Я прочитал только несколько описаний сюжета, в частности, в Википедии. Тем не менее, я благодарен автору романа, поскольку он стимулировал мой интерес к Задаче"
Список литературы
-
Хайрер Э., Нерсетт С., Ваннер Г. "Решение обыкновенных дифференциальных уравнений"
-
Виктор Себехей "Теория орбит"
-
Егоров В.А. "О некоторых задачах динамики полета к Луне"
-
Ana Hudomal "New Periodic Solutions to the Three-Body Problem and Gravitational Waves"
-
Emily M. Zimovan Spreen "Trajectory design and targeting for applications to the exploration program in cislunar space"
Автор: belch84






