
Привет! В моей работе часто возникают задачи на исследование влияния факторов, на которые мы можем оказывать продуктовое влияние, на целевые метрики сообществ ВКонтакте. Один из возможных способов решения подобных задач — обучение ML‑моделей и последующий анализ значимости признаков в них. Базовым подходом видится использование графиков из библиотеки shap. Однако наиболее популярным является summary_plot, хотя он и повышает интерпретируемость модели, но отвечает не на все возникающие вопросы.
Меня зовут Сергей Королёв, я продуктовый аналитик в бизнес‑юните СМБ в VK, занимаюсь улучшением опыта предпринимателей на нашей платформе. В этой статье я представлю свое решение по кастомизации shap.dependence_plot для простого восприятия графиков влияния факторов на целевую метрику.
Недостатки summary_plot
Рассмотрим summary_plot на примере датасета о выживаемости пассажиров «Титаника». В качестве модели используем catboost с минимальной предобработкой признаков и оставим только количественные и категориальные признаки с ограниченным количеством категорий.
Код обработки данных и обучения модели:
titanic_train = pd.read_csv('titanic/train.csv')
titanic_train['Age'] = titanic_train.Age.fillna(titanic_train.Age.dropna().median())
titanic_train['Embarked'] = titanic_train.Embarked.fillna(titanic_train.Embarked.dropna().mode()[0])
X = titanic_train.drop(columns=['Survived', 'Cabin', 'Ticket', 'PassengerId', 'Name'])
y = titanic_train.Survived
scale_pos_weight = int(y.value_counts()[0] / y.value_counts()[1])
model = CatBoostClassifier(
subsample=0.66, rsm=0.5, depth=3, cat_features=['Sex', 'Embarked'],
random_seed=42, verbose=False, scale_pos_weight=scale_pos_weight
)
model.fit(X, y)Построенная модель обучена на признаках:
-
Pclass— класс, которым путешествовал пассажир; -
Sex— пол пассажира; -
Age— возраст пассажира; -
SibSp— количество братьев и сестер или супругов на борту; -
Parch— количество родителей или детей на борту; -
Fare— стоимость билета; -
Embarked— порт посадки.
Их значимость для модели можно отобразить с помощью кода:
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X)
shap.summary_plot(shap_values, X);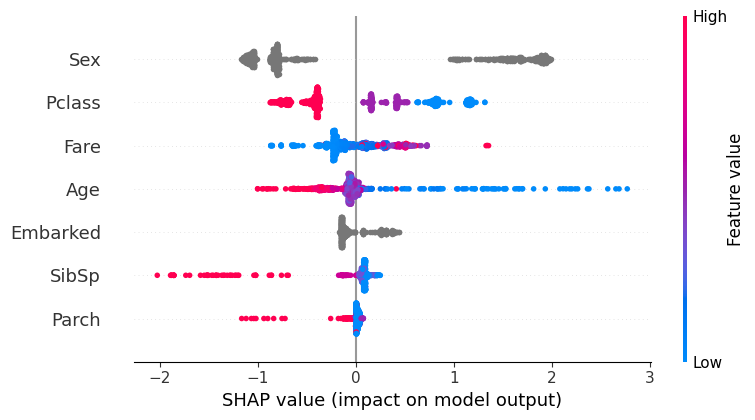
По графику можно понять, что пол пассажира и класс являются наиболее важными признаками. И заметить, что пассажиры с большими значениями класса, соответствующими более низким классам обслуживания, по мнению модели имели меньше шансов выжить. Но есть ряд вопросов, которые важны при анализе влияния признаков на целевую переменную, и которые нельзя понять по этому графику:
-
Какие значения категориальных признаков и как влияют на решения, принимаемые моделью?
-
Какие абсолютные значения количественных признаков являются высокими, а какие низкими?
-
Сколько объектов имеют определённое значение признака?
-
Есть ли доминирующие признаки, или их влияние на решение модели сопоставимо?
На все эти вопросы можно ответить, кастомизировав другой тип графиков, доступный в библиотеке SHAP — dependence_plot.
Обход недостатков summary_plot
Влияние конкретных значений категориальных и количественных признаков на решения, принимаемые моделью, можно увидеть, используя dependence_plot, который строится для каждого признака отдельно. На графиках по оси Х выводится значение признака, а по оси Y — значение SHAP для него.
Код dependence plot:
shap.dependence_plot('Sex', shap_values, X, interaction_index=None)
shap.dependence_plot('Age', shap_values, X, interaction_index=None)Для категориальных признаков график выглядит так:
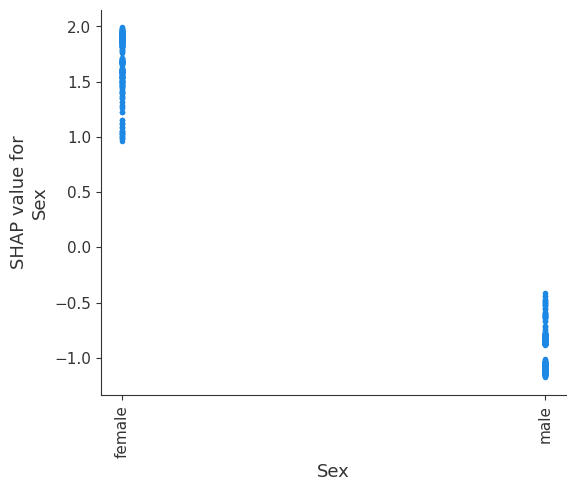
Для количественных переменных:
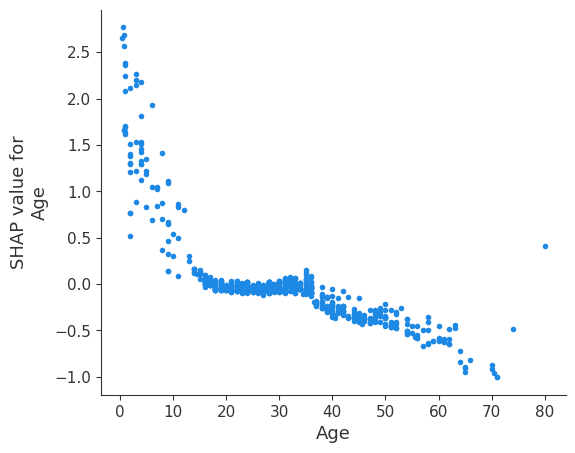
Для наглядности можно добавить сетку и ярче выделить нулевую линию, отделяющую позитивное влияние от негативного.
Чтобы по графику можно было понять, какие значения признака встречаются в данных чаще, для количественных признаков можно использовать график типа scatter из библиотеки shap, который совмещает dependence_plot с гистограммой распределения признака:
shap_explainer = explainer(X)
shap.plots.scatter(shap_explainer[:, 'Age']);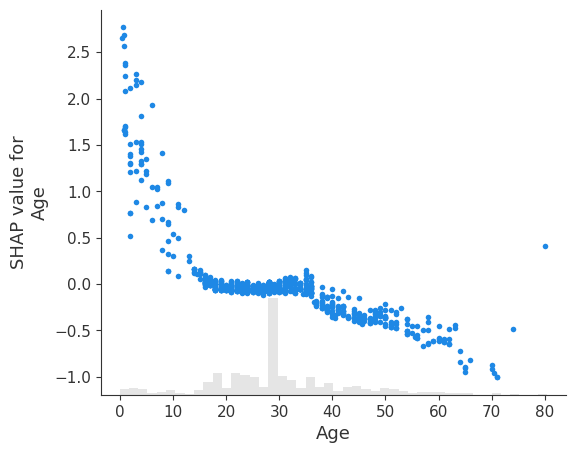
Однако такой вид графиков не поддерживает категориальные переменные. Поэтому более универсальным решением будет использование параметра прозрачности alpha для dependence_plot, за счет снижения которого более часто встречающиеся значения будут отображаться на графике интенсивнее. Код dependence plot с настройкой прозрачности и сеткой:
fig, ax = plt.subplots();
ax.grid();
plt.axhline(y=0, color='grey', linewidth=2.5);
shap.dependence_plot('Age', shap_values, X, interaction_index=None, alpha=0.2, ax=ax);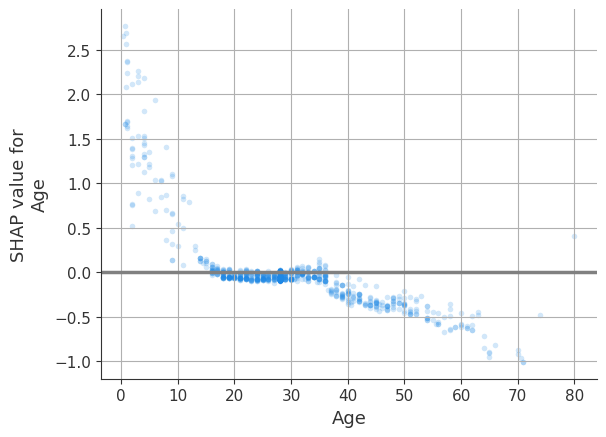
Последним важным для меня недостатком summary_plot стало то, что он по умолчанию сортируется по среднему вкладу признаков в решения модели, но не отображает этот вклад. Чтобы оценить его, можно воспользоваться отдельным графиком типа bar.
shap.plots.bar(shap_explainer)
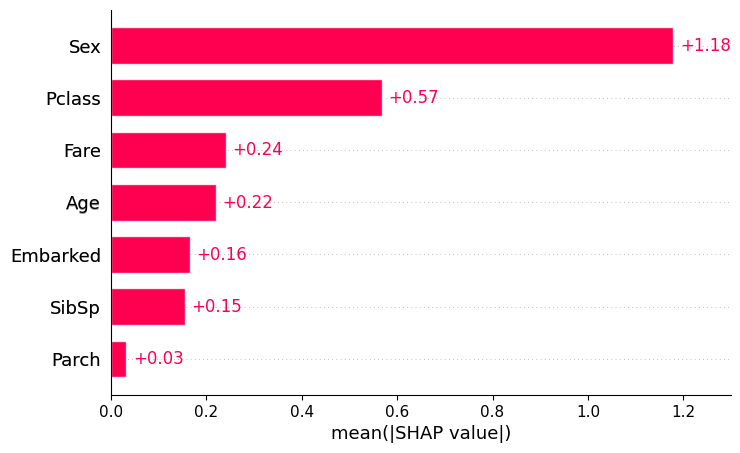
Либо можно собрать dependence_plot по всем признакам на одном графике и вынести на них относительную значимость, рассчитанную по матрице с SHAP values.
После устранения с помощью dependence_plot недостатков, характерных для summary_plot, возникает ряд дополнительных проблем, снижающих удобство пользования графиком:
-
Некоторые количественные признаки, с которыми мне приходится работать на практике, могут иметь распределение с длинным правым хвостом, близкое к логнормальному. Или вовсе иметь большую часть нулевых значений и длинный правый хвост. Поэтому хочется иметь возможность отсекать выбросы на графике, чтобы смотреть на основные зависимости в удобном масштабе. Для отсечения выбросов я использовал порог в 1,5 межквартильных размаха от первого и третьего квартилей. Либо, если межквартильный размах для признака равен 0, то по 2,5 % значений с каждой стороны.
-
Категориальные признаки также могут содержать много категорий, одновременное отображение которых на одном графике сделает его нечитаемым. Как правило, среди этих категорий будет несколько частых и много редких. Поэтому хочется иметь фильтрацию, оставляющую ограниченное количество категорий с наибольшим количеством наблюдений.
При исследовании влияния признаков на целевую переменную также может возникнуть желание смотреть на те наблюдения, где ML-модель в своих предсказаниях близка к реальному значению целевой переменной. Поэтому полезно добавить отсечение задаваемого процента наименее точных предсказаний.
Для удобства использования все описанные идеи можно реализовать в рамках одной функции.
Итоговая функция отрисовки значимости признаков
def plot_shap_feature_importances(
model, X_test, y_test, continuous_target, predictions_trashold, cat_features,
alpha, plots_folder, target_col
):
'''
:param model: Обученая ML-модель (на деревьях)
:param X_test: Тестовый датафрейм с предикторами
:param y_test: Тестовый датафрейм с таргетом
:param continuous_target: Флаг непрерывной целевой переменной (регрессионная модель)
:param predictions_trashold: Доля откидываемых наблюдений с наибольшими ошибками предсказания
:param cat_features: Список категориальных фичей
:param alpha: Непрозрачность заливки точек
:param plots_folder: Путь к папке сохранения графиков
:param target_col: Название целевой переменной для сохранения графиков
'''
# Отбрасываем заданный процент не точных предсказаний
if continuous_target:
y_preds = model.predict(X_test)
else:
y_preds = model.predict_proba(X_test)[:, 1]
errors = np.abs(y_test - y_preds)
mask = errors <= np.quantile(errors, 1 - predictions_trashold)
X_test_for_plot = X_test[mask].copy()
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_test_for_plot)
# Очистка чтобы график не накладывался на предыдущий
plt.close('all')
shap.summary_plot(shap_values, X_test_for_plot, show=False);
plt.savefig(f'{plots_folder}/shap_summary_{target_col}.png', bbox_inches='tight');
# Смотрим относительное влияние фичей
vals = np.abs(shap_values).mean(0)
fi = pd.DataFrame(
list(zip(X_test_for_plot.columns, vals)),
columns=['features', 'importance']
)
fi.sort_values(by=['importance'], ascending=False, inplace=True)
fi['importance'] = fi.importance / fi.importance.sum()
# Отрисовываем отдельные графики
subplots_number = len(X_test_for_plot.columns)
nrows = int(np.ceil(subplots_number / 2))
fig, axes = plt.subplots(
nrows=nrows, ncols=[1, 2][int(subplots_number > 1)],
figsize=(12, nrows * 5), layout='constrained'
)
for idx, col in enumerate(zip(fi.features.to_list(), fi.importance.to_list())):
if col[0] in cat_features:
# Для категориальных фичей отрисовывем топ-10 категорий
important_cats = list(X_test[col[0]].value_counts().index)
important_cats = important_cats[:min(10, len(important_cats))]
temp_df = X_test_for_plot[X_test_for_plot[col[0]].isin(important_cats)].copy()
else:
# Для количественных смотрим базовую стратегию отсечения по межквартильному интервалу
q1 = X_test[col[0]].replace(np.inf, np.nan).dropna().quantile(0.25)
q3 = X_test[col[0]].replace(np.inf, np.nan).dropna().quantile(0.75)
iqr = q3 - q1
min_trashold = max(
q1 - 1.5 * iqr,
X_test[col[0]].replace(np.inf, np.nan).dropna().min()
)
max_trashold = min(
q3 + 1.5 * iqr,
X_test[col[0]].replace(np.inf, np.nan).dropna().max()
)
if X_test[col[0]].nunique() <= 50:
# Если в количественной фиче не более 50 значений, оставляем их все
temp_df = X_test_for_plot.copy()
elif iqr > 0:
# Если есть межквартильный размах, отсекаем лежащее за перделеами 1.5 его величин
temp_df = X_test_for_plot[
(X_test_for_plot[col[0]] >= min_trashold) &
(X_test_for_plot[col[0]] <= max_trashold)
].copy()
else:
# Если межквартильный размах равен 0, то отсекаем по 2.5% с каждой стороны
q025 = X_test[col[0]].replace(np.inf, np.nan).dropna().quantile(0.025)
q975 = X_test[col[0]].replace(np.inf, np.nan).dropna().quantile(0.975)
temp_df = X_test_for_plot[
(X_test_for_plot[col[0]] >= q025) &
(X_test_for_plot[col[0]] <= q975)
].copy()
# Смотрим SHAP только для релевантных наблюдений
shap_values = explainer.shap_values(temp_df)
# Определяем позицию графика для отрисовки текущей фичи
if nrows > 1:
ax = axes[idx // 2, idx % 2]
elif subplots_number > 1:
ax = axes[idx % 2]
else:
ax = axes
# Отрисовываем график по фиче
shap.dependence_plot(
col[0], shap_values, temp_df, ax=ax,
interaction_index=None, show=False, alpha=alpha
)
ax.grid();
xlims = ax.get_xlim()
ax.hlines(y=0, xmin=xlims[0], xmax=xlims[1], color='grey', linewidth=2.5)
ax.set_title(f'{col[0]} ({col[1]:.1%})');
if col in cat_features:
ax.tick_params(axis='x', labelsize=6, labelrotation=90)
# Удаляем не используемый график
if (nrows > 1) and (subplots_number % 2 == 1):
fig.delaxes(axes[nrows - 1][1])
# Сохраняем полученный график
plt.savefig(
f'{plots_folder}/shap_dependencies_{target_col}.png', bbox_inches='tight'
);В качестве входных аргументов эта функция принимает:
-
обученную модель;
-
тестовый набор предикторов и значения целевой переменной в тестовой выборке;
-
флаг непрерывности переменной для определения способа оценки ошибок предсказания;
-
долю откидываемых наименее точных предсказаний;
-
список категориальных признаков для определения способа отсечения выбросов по каждому из предикторов;
-
параметр прозрачности;
-
а также папку для сохранения графиков и общий модификатор названия для них.
По результатам работы данная функция сохраняет summary_plot и собранный график состоящий из dependence_plot для каждой фичи в указанную папку под указанным названием.
До и после
С графика с одной визуализацией мы начинали анализировать влияния признаков на целевую переменную.
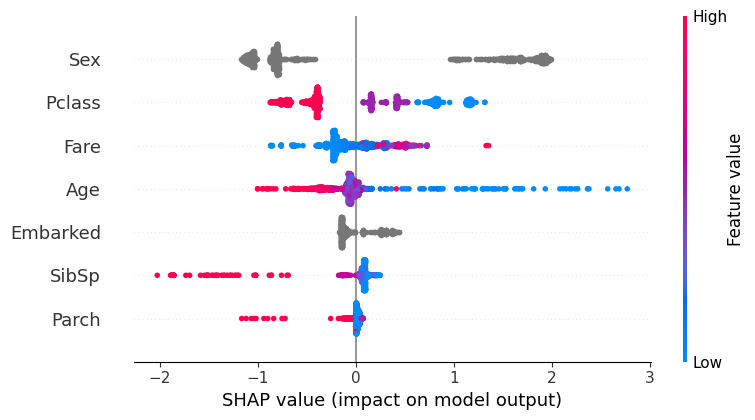
И пришли к графику, объединяющему несколько подграфиков, на котором каждый признак вынесен отдельно. А каждый из подграфиков показывает влияние конкретных значений признака на решение модели и относительную значимость признака для решений модели.
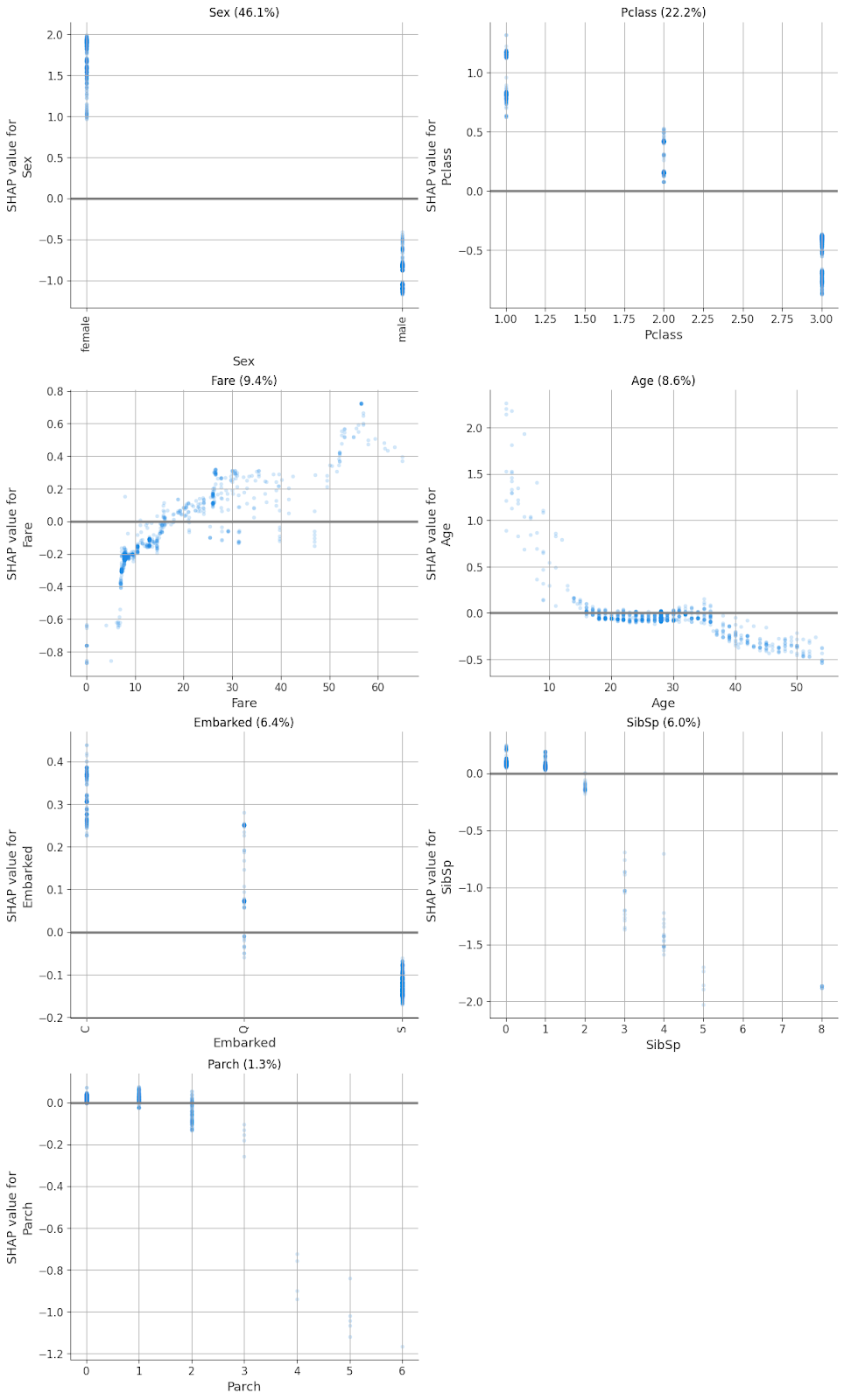
Заключение
После создания этой функции я стал использовать её при отрисовке графиков для анализа влияния признаков на целевые метрики в обученных ML-моделях. Её основные преимущества для меня по сравнению со стандартным summary_plot:
-
По одному графику можно понять важность признаков и их влияние на решения модели.
-
Проще визуально воспринимать пороговые значения, с которых начинается позитивное влияние на целевую переменную.
-
Проще донести интерпретацию модели до менеджеров.
Автор: Сергей Королев


