Рисуем рабочий процессор в Paint и запускаем на нём ОС | Ритуал по призыву демона Тьюринга

Однажды в тёмном-тёмном городе, в тёмном-тёмном подвале, очередной обезумевший контентмейкер за паяльной станцией подключал программатор к умному термосу.

Термос этот он нашёл на улице и хотел перепрошить его маленький и беззащитный Cortex-M0+.
Человек бредил. Раз в пару минут его глаза загорались и он издавал душераздирающий крик: «Если что-то существует, то на этом можно запустить Doom!».

Но действительно ли это так? И что вообще значит «запустить»?

Почему нельзя просто вывести изображение логотипа или распиновать VGA для вывода изображения на дисплей абсолютно любого устройства?

Ведь все так и делают)

Сегодня мы узнаем, как может выглядеть самый примитивный девайс, обладающий свойствами компьютера и способный полноценно запустить любой алгоритм.

С этой целью мы обратимся к немного странным, но всё же незаслуженно забытым языкам программирования. Когнитивная сложность дальнейшего текста обещает быть минимальной, даже непосредственно ассемблерного программирования в статье не будет.

Ну а если вы всё ещё здесь — добро пожаловать под кат.

Думаю, ни у кого не возникает сомнений, что современный компьютер — комплексная параллельная структура, синхронизируемая воедино при помощи массы генераторов частот.
Но можно ли в таком случае считать одиночный микроконтроллер компьютером?

Формально даже примитивный калькулятор из канцелярского магазина выполняет логические операции над абстракциями и имеет интерфейсы ввода/вывода для пользователя, но становится ли он от этого компьютером?

Как вы понимаете, в эпоху появления вычислительных машин каждый хотел придумать свою спецификацию и описать «настоящий компьютер», чтобы назвать его своим именем. В первую очередь для этого нужно описать то, что выполняет компьютер — алгоритм.

Алгоритм по Тьюрингу — совершенно математическая вещь. Функция, которая связывает множество входных состояний с выходными в соответствии с некоторым множеством памяти.

Алгоритм выполняется так называемой Машиной Тьюринга — собственно, цикличным применением этой самой функции над лентой.

Но в реальном компьютере нет ни бесконечной ленты, ни машины тьюринга, ни математических функций. Математическое описание алгоритма абсолютно непрактично. Тем не менее это не отнимает у него права на существование — все ведь любят полноту по Тьюрингу.

Сегодня я хотел бы показать вам, что если что-то является полным по Тьюрингу, то можно не только запустить на этом алгоритм, но и эмулятор любого другого Тьюринг-полного исполнителя. В качестве такого устройства мы будем рассматривать экстремальную машину Тьюринга с минимальным размером таблицы соответствия.

У нас было два символа в алфавите, одна инструкция на весь ассемблер, 5 программируемых калькуляторов или ардуино, ядро операционной системы, наполовину состоящее из нулей, и целое море разноцветных пикселей. Не то чтобы всё это было категорически необходимо в статье, но если уж начал собирать коллекцию, то к делу надо подходить серьёзно.

Оглавление

1. Введение
2. Оглавление
3. Эмуляция
   • Эмуляторы
   • Необычные исполнители
4. URISC
5. Дзен Forth
   • Конкатенативный язык
   • Subleq процессор
   • Демонстрация Forth
6. Piet
   • Компиляция ядра
   • Рисуем процессор
7. Заключение

Эмуляция

Слово это может ассоциироваться у вас вообще с чем угодно, но сейчас мы остановимся на эмуляции архитектуры процессора.

Архитектура процессора — реальное внутренне устройство этой коробочки с транзисторами. Определяет функции, связанные с конкретными ножками процессора — инструкции.

Для каждого физического процессора строго определён набор инструкций — instruction set. Повсеместно используются CISC и RISC (плюс MISC в качестве экзотики). Набор последовательно записанных инструкций — алгоритм на ассемблере.

Как следствие, под каждую физическую архитектуру процессора нужно описывать конкретный ассемблер и писать под него компиляторы для базовых ЯП. Именно по этой причине приложения не всегда обладают кроссплатформенностью.

Однако можно портировать ассемблер одного процессора на другой. Конечно, если набор инструкций первого процессора можно перевести на язык другого.

Жутко неудобно, верно? Вот бы всё работало на машине Тьюринга...

Поскольку один ассемблер не всегда можно перевести в другой, то у нас не остаётся выбора, кроме как подниматься выше в уровнях абстракции. Мы просто будем воссоздавать механизм работы одного процессора на ассемблере другого. По сути — создавать виртуальную копию первого. Этот процесс и называется эмуляцией.

Веселье же приходит с осознанием того, что никто не запрещает нам выполнять эмуляцию на ещё более высоких уровнях абстракции. Мы можем взять и написать эмулятор процессора приставки Dendy на Python, а потом гордо об этом писать в резюме. Не для этого ли нужны платные онлайн-курсы?

Не можешь бороться с чем-то — возглавь это. Следуя именно этой догме, мы сейчас возведём концепцию высокоуровневой эмуляции в абсолют.

Эмуляторы

Представляю вам нашего сегодняшнего персонажа: это Антон. Антон очень любит хвастаться друзьям, что он программист на языке Пáйтон. Но однажды в компании друзей Антон услышал мнение, что человек, который не шарит за low-level архитектуру, не имеет права называть себя программистом. Антона это задело и он не мог спать ночью, думая только о том, что он не настоящий программист.

После мучительного брейншторма и тренировки на лыжах в лесу он всё-таки решился ковать свою судьбу самостоятельно. Он решил во что бы то ни стало написать полностью свой эмулятор.

На просторах сети Интернет ему подсказали, что когда программисты пишут свои первые «эмуляторы», они зачастую начинают с контроллера intel 4004 (см. «Сказ о том, как я эмулятор Intel 4004 на Python писал»), ведь именно он вылазит в гугле по запросу самый первый процессор.

Начав изучение теории, Антон сталкивается c официальным datasheet набора инструкций 4004 и видит это:

Серьёзно? Около 40 инструкций?

Именно так. И каждую из них нужно реализовать на пресловутом Python)

Нет, я, конечно, не спорю, что эмуляция ADD при помощи оператора "+" Питона это круто (см.«Так сколько на самом деле строк на C нужно, чтобы выполнить a + b в Python?»), однако она является абсолютно неспортивным занятием. Мы ещё не успели заняться написанием эмулятора, как почувствовали его рутинность и бесполезность. Нужен иной подход.

И тут на сцену выходят кастомные ассемблеры. Они же являются весьма своеобразным феноменом. Антон решил, что он сделает эмуляцию своего процессора с его авторским набором инструкций. Он ведь как-никак творец — так кто же ему запретит.

Он ещё не знает, что после такого у него не останется друзей вообще и он будет до конца жизни пилить собственный ассемблер на Python в одиночку. Когда-нибудь он разработает свой CISC, в котором будет более 1000 инструкций, и всё равно не сможет на нём ничего запустить.
Процессор Антона абсолютно несовместим с существующим ПО. Конечно, рано или поздно Антон напишет под него свои компиляторы и софт, но мы ведь сразу будем умнее его, верно?

Как вы уже могли догадаться, я хочу запустить что-либо классическое на машине Тьюринга или подобной ей. Например, эмулятор процессора 4004 с запущенным на нём алгоритмом поиска простых чисел. Можно и любой другой Proof of concept. Суть именно в том, что в теории машину тьюринга можно сделать вообще из любых ресурсов. Это будет означать нашу абсолютную победу и способность в дальнейшем запустить любой софт на любом калькуляторе.

Итак, наша задача сейчас — запустить что-то крутое на примитивном исполнителе, по которому даже сразу и не скажешь, что он вообще является процессором. Отличный материал на эту тему я читал около года назад, и теперь просто обязан оставить ссылку на эту замечательную статью: «Симулятор x86 подобного процессора на машине Тьюринга». Пусть автор по факту и придумал свой ассемблер для упрощения итоговой конструкции, но он честно портировал стандартные инструкции на ленту Тьюринга. Под конец он запустил пусть и не сложный софт, но простейшие программы на ассемблере вместе с визуализацией их выполнения на ленте — это весьма эффектный результат.

Необычные исполнители

Тогда у меня в голове и была посеяна идея развития её до универсального исполнителя. Конечно, реализовать исполнитель тоже хотелось бы на очень специфичном инструментарии. Изначально я хотел взять игру с возможностью реализации полноценной логики и создать в ней машину Тьюринга в явном виде. Найти способ эмулировать на ней какой-либо стандартный ассемблер и запустить прикольные демонстрации.

Первые кандидаты, которые мне пришли в голову:

• Factorio. Логические элементы в этой игре это чистейший ад — они являются жуткой помесью аналоговых элементов и сигнальных флагов. Из готовых наработок я нашёл это: готовый дизайн процессора с 29 инструкциями, который едва ли тянет на PoC — ясно, что на нестандартном instruction set не запустить нормальных тестов.

  

  Тем не менее автор утверждает, что всё должно работать именно так, как мы ожидаем.

  В то же время есть люди, которые решили чуть более общую задачу и написали переводчик из VHDL в чертежи факторио.

  

  Что по факту является дичайшим оверкиллом. Подобный компилятор позволяет эмулировать на комбинаторах практически любую реальную схемотехнику и не оставляет нам вообще никакого простора для творчества.

• Terraria. Тут уже всё давно придумано на кастомном ассемблере. Последнее время всё чаще натыкаюсь на новости вида «В terraria сделали компьютер и (! почти!) запустили на нём ...». Речь тут идёт про достаточно милый проект Computerraria.

  

  Тут уже всё честно — автор утверждает, что его процессор «RISC-V совместим» и даже запускает на нём порты Doom/Tetris, прокручивает BadApple и симулирует Game of Life.

• Game of life. Кстати, игру «жизнь» тоже можно рассматривать как Тьюринг-полный процессор. Думаю, вы и так видели массу видео с реализацией тех или иных алгоритмов поверх неё. На ютубе можно найти как мета-жизнь на движке из самой себя, так и «компьютеры» наподобие этого:
• Minecraft. С вашего позволения не буду акцентировать на нём внимание.

  

  Ситуация тут аналогична Terraria, ничего нового туда уже не преподнести, да и желание совершенно отсутствует.

• TIS-100. Я бы сказал, что эта игра незаслуженно игнорируема большинством — и оказался бы не прав. Точнее намеренно бы лукавил. TIS — это буквально симулятор написания кода на ассемблере. Игра, к которой прилагается документация вместо нормальных интерфейсов или прогрессии. Позиционирует себя как «головоломка для программистов», но по факту достаточно уныла даже для оных. После моих тщетных попыток прикрутить к ассемблеру в ней классический ввод/вывод при помощи кастомных карт и модификаций, я пришёл к выводу, что это абсолютно нецелесообразно.

  

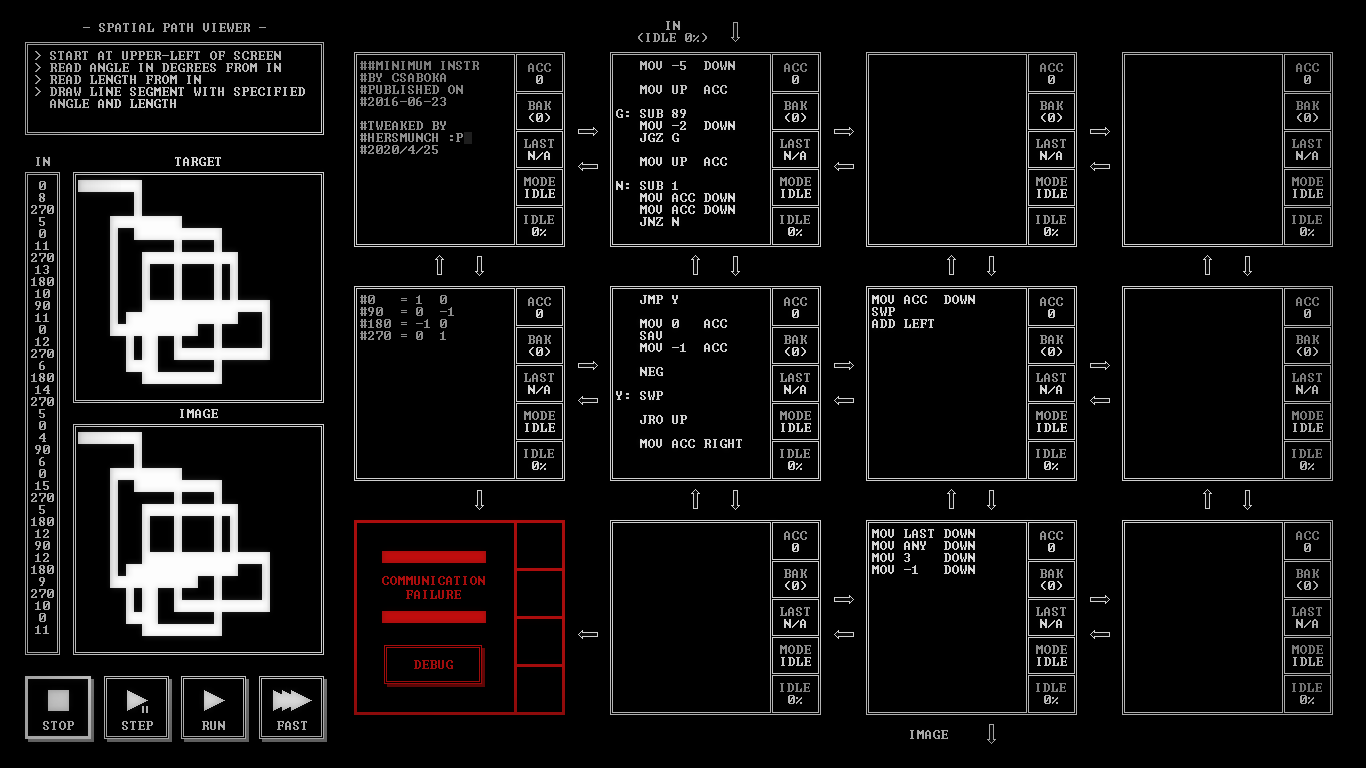
  Тем не менее я просто обязан был её упомянуть в контексте этой статьи. Она вписывается в конечную идею этого текста как нельзя лучше.

Когда надежда практически угасла, а мир поглотило серое ничто, появилось первородное пламя URISC.

URISC

URISC (как RISC) или OISC (как CISC). Судя по забавному слову Ultimate в расшифровке аббревиатуры и мимикрии под реальные стандартные наборы инструкций, зверюшка эта обещает быть специфичной и не особо юзабельной.

И действительно, за этим названием скрывается сразу несколько принципиально разных ассемблеров с одной (для каждого своей) инструкцией.

При этом любой из них является Тьюринг-полным, а программы на них выглядят как многократное условное повторение одного и того же действия над памятью. Сейчас разберём на примерах.

На Википедии сказано, что самым популярным вариантом единственной инструкции является RSSB — «вычесть и пропустить следующую инструкцию, если вычитаемое было больше уменьшаемого» (англ. reverse-subtract and skip if borrow). Однако когда речь заходит о столь нишевом развлечении, слово «популярным» становится неуместным. Я ни разу не видел RSSB где-либо кроме этой статьи на Википедии, да и инструкция кажется довольно сложной в использовании. Программы на таком ассемблере же будут жутко громоздкими в связи с возможностью скипать лишь одну инструкцию.

Конечно, никто не станет писать непосредственно на URISC-ассемблере, но вот изготовить компилятор кому-нибудь всё-таки придётся. Так вот на RSSB ядро получилось бы ну уж очень жирным. Есть ещё и концептуально другие FlipJump и BitBitJump, однако на них я подробно останавливаться не стану. Они основаны на битовых операциях и куда менее интуитивны. Если же они вам действительно интересны, то на английской Википедии о них весьма неплохо написано. Нам будет интересен логический брат RSSB, но с чуть более перегруженной сигнатурой — SUBLEQ.

Subleq — «вычесть и перейти, если результат не положительный» (англ. subtract and branch unless positive). Тут уже используется более комплексное и удобное действие «branch», или просто переход в указанный адрес памяти для дальнейшего выполнения его как асм-кода. По сути, это реализация динамического перемещения по программе.

С серьёзным лицом этими ассемблерами, конечно, никто не занимается. Это тот случай, когда даже красивую картиночку или логотип по названию найти нельзя. В Steam правда есть копия TIS-100, в которой в качестве языка для решения задач используется subleq. Называется она весьма оправданно SIC-1.

Кстати, настоящие фанаты эзотерики подняли свой вики-сайт esolangs.org, на котором мы с вами сегодня будет искать информацию как про URISC, так и про (! спойлер!) Piet с Forth. Жалко, кстати, что на Хабре из перечисленных языков есть хаб только для Forth (и тот с нулевым рейтингом).

В общем, механизм работы нашего абстрактного процессора уже на поверхности, так что предлагаю отвлечься на софт, который мы будем на нём запускать.

Дзен Forth

Йоды магистра тайна речи раскрыта:
Старым Форта программистом был он просто.

Написано на Википедии с явным намёком на необходимый реверс строк для удобного чтения. В действительности это не совсем так. И да, это язык программирования. Некоторые гурманы даже могут классифицировать его как операционную систему. Дзен Форта заключается в его абсолютном минимализме и мета-компилировании.

С минимализмом всё просто — это расширенный язык стекового калькулятора или, с обывательской точки зрения, калькулятора обратной польской нотации.

Писать и читать код на нём неподготовленному человеку может быть неимоверно больно, особенно если вы не были ранее знакомы с Lisp или Prolog.

Однажды мне довелось общаться с одним дедулей-профессором, который был настоящим Lisp-эстетом. В общем, стояв у подножия всего программирования и алгоритмики, какие они есть на текущий момент, он настолько преисполнился в своём сознании, что стал писать только на Lisp и только в своём же интерпретаторе, написанном тоже на Lisp. Наверное, такие как он и являются атлантами, что держат на плечах хостинг esolangs.

А вот философия мета-программ — штука уже не столь очевидная. Начнём, пожалуй, с косвенных признаков:

1. Ядро Форта написано на форте.
2. Ядро Форта может компилировать любые программы на форте в целевой ассемблер (оно является компилятором).
3. Ядро Форта скомпилировано в ассемблер самим собой (оно является компилятором для самого себя)

Из этого вытекает очевидная кросс-компиляция, масштабируемость и другие эзотерические суперспособности этого языка.

Собственно, на днях мне попался на глаза репозиторий, содержащий мета-компилятор Forth, написанный на Forth и компилирующий программы на Forth в subleq ассемблер!

Ядро это просто гигантское, так что его я разбирать на косточки сейчас не стану. Написано оно достаточно читабельно, и вполне подлежит самостоятельному изучению, если знать синтаксис Forth.

Кстати, я ещё не упомянул, что пусть синтаксис Forth и плохо читаем, но он максимально прост концептуально. Программа на Forth — это просто последовательный поток «слов», записанных через пробел. Как я уже писал выше, подобный способ нотации подразумевает использование принципов стекового калькулятора, т.е. программа для сложения чисел 2 и 3 и вывода результата на экран выглядит так: 2 3 + . (. — слово для вывода верхнего элемента стека на экран). Слова делятся на эффекты стека и числа. Числа являются единственной сущностью в Forth, которая просто добавляется в стек, когда до неё добирается исполнитель. Эффекты же описываются специальным wordlist`ом, свойственным каждой конкретной спецификации вроде нашего сегодняшнего eForth (об этом позже).

Другими словами, если очередное слово программы присутствует в wordlist, то оно будет применено как эффект к стеку. Это может быть реверс, взятие элемента, печать, арифметическая операция и т. д.

Описанная выше программа 2 3 + . последовательно добавляет в стек числа 2,3 и применяет над стеком вида 2 3 <- эффект +, который превращает его в стек 5 <-. Далее верхний элемент стека отправляется пользователю в соответствии с реализацией слова . (точка).

При этом такого инструментария вполне достаточно для создания поверх него других абстракций. Из того, что я нашёл: Эмулятор 6502 процессора, Интерпретатор диалекта Lisp.

Конкатенативный язык

Самая, вероятно, принципиальная особенность этого языка — это его принадлежность к конкатенативной парадигме программирования. Она по факту является декларативной на стероидах. Основной же её принцип таков: «Последовательная запись фрагментов кода выражает суперпозицию этих фрагментов» или с математической точки зрения «Конкатенация выражает композицию».

Конечно, в Forth есть реализация и циклов, и ветвлений, и даже функций, однако этим я предлагаю заняться уже после запуска интерпретатора. Как я уже писал выше, умелец Richard James Howe уже сделал и выложил в открытый доступ ядро subleq мета-компилятора для eForth. Он даже написал об этом целую книгу и продаёт её на Амазоне, так что в чужой огород я, с вашего позволения, лезть не стану. Вот его промо-страница https://howerj.github.io.

Subleq-процессор

Сейчас нас интересует реализация самого subleq-процессора на C, которую howerj заботливо оставил нам в своём репозитории с eForth.

#include <stdint.h>
#include <stdio.h>

typedef uint16_t u16;
static const u16 n = -1;
static u16 m[1<<16], pc = 0, prog = 0;

int main(int argc, char **argv) {
	for (long i = 1, d = 0; i < argc; i++) {
		FILE *f = fopen(argv[i], "rb");
		if (!f)
			return 1;
		while (fscanf(f, "%ld,", &d) > 0)
			m[prog++] = d;
		if (fclose(f) < 0)
			return 2;
	}
	for (pc = 0; pc < 32768;) {
		u16 a = m[pc++], b = m[pc++], c = m[pc++];
		if (a == n) {
			m[b] = getchar();
		} else if (b == n) {
			if (putchar(m[a]) < 0)
				return 3;
			if (fflush(stdout) < 0)
				return 4;
		} else {
			u16 r = m[b] - m[a];
			if (r == 0 || r & 32768)
				pc = c;
			m[b] = r;
		}
	}
	return 0;
}

Выглядит она вот таким незамысловатым образом. Правда есть вероятность, что человек, плохо знакомый с С, выпадет в осадок после прочтения этого весьма специфичного кода. Таковым я его называю, так как он пестрит побитовыми операторами и по факту нативно использует ограничения 16-битных integer'ов для ограничения битности этой «виртуальной машины».

Не спорю, что в результате этот код работает просто молниеносно. Однако всё же считаю нужным перевести его на чистый Python и максимально уменьшить в размерах — позже будет понятно зачем.

Для начала загрузим наше ядро из файла, переданного в аргументе запуска:

m = [0] * 65536

i = 0
for image in sys.argv[1:]:
    with open(image) as f:
        for line in f.readlines():
            for v in line.split():
                m[i] = int(v)
                if m[i] < 0: m[i] = 65535 + m[i] + 1
                i = i + 1

Получаем список integer'ов с названием m. Он и будет являться рабочим пространством нашей машины. Он будет выполнять роль как постоянной памяти, так и оперативной. Соответственно, наша операционная система тоже содержится в нём. Это и есть наша лента.

После загрузки ядра из файла лента выглядит примерно так:

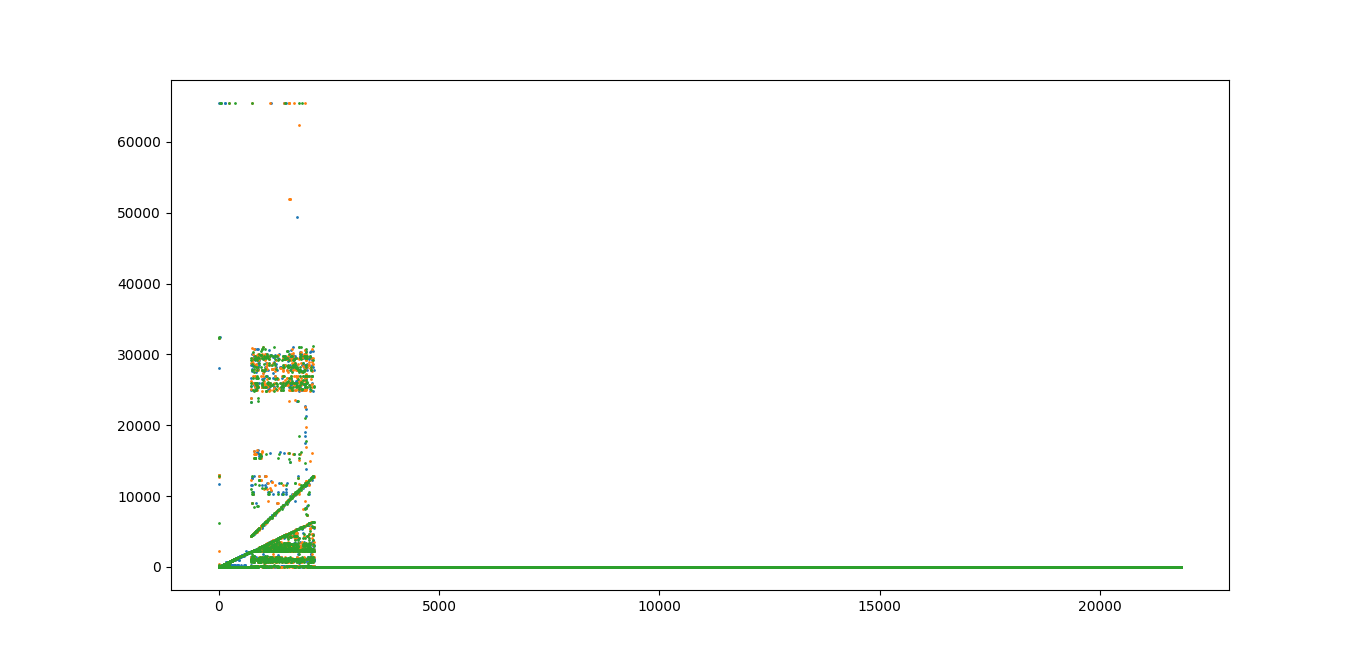
Вы можете заметить, что само ядро занимает меньшую часть пространства, да и вообще плохо видно. Сами 6000 чисел полезной subleq-нагрузки выглядят так:

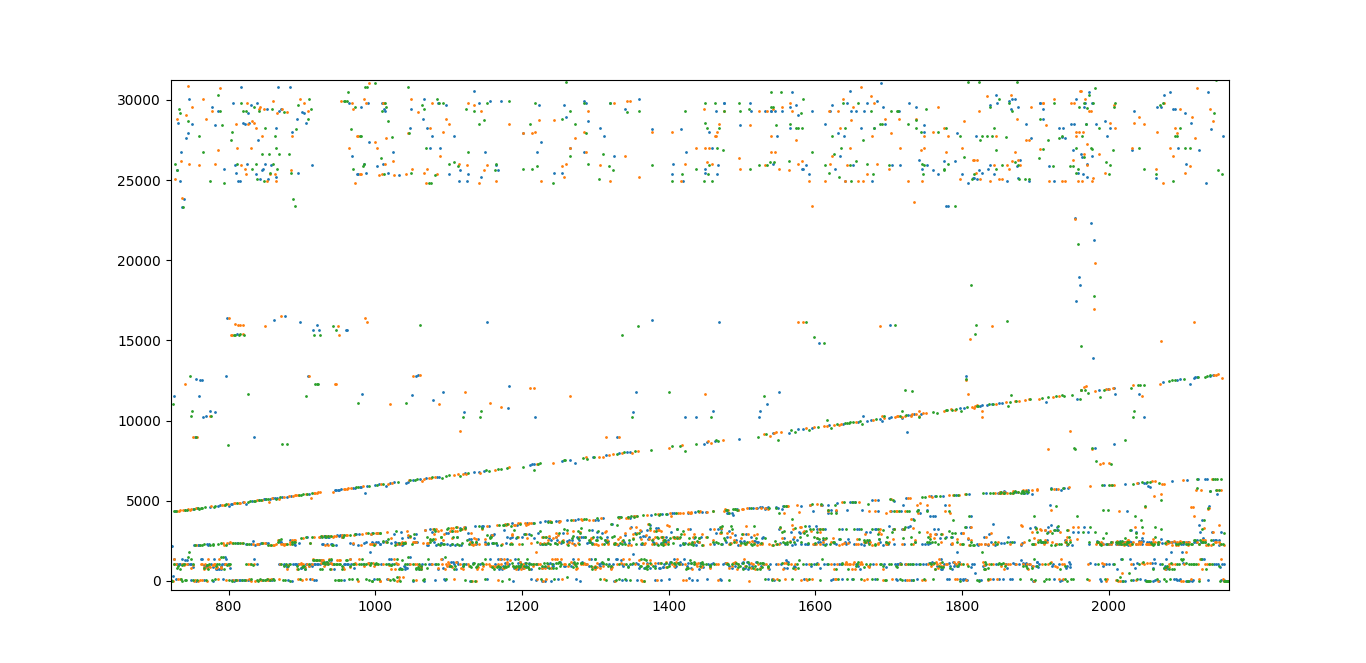
Тут уже просматриваются паттерны и маршруты, по которым может ездить исполнитель. Пришло время вдохнуть в нашу матрицу жизнь. Подготовим функции для считывания stdin и вывода пользователю stdout.

stdin = lambda: ord(sys.stdin.read(1))

stdout = lambda c: print(chr(c), end="", flush=True)

Практически всё готово. Остаётся реализовать саму инструкцию SUBLEQ и засунуть её в бесконечный цикл. Судя по оригинальному коду, для ввода и вывода информации используется -1 адрес на ленте. С поправкой на переполнение типа uint16_t, это будет равносильно адресу 65535.

Вы можете справедливо заметить, что в Python можно получить и настоящий Unsigned integer 16bit при помощи каких-нибудь ctypes или банально numpy.uint16. Работать это будет, однако в разы медленнее нативного типа. Даже память мы таким образом практически не сэкономим ввиду издержек портирования си-примитивов в Python.

pos = 0 #Наша позиция на ленте (каретка)
while 1:

    #ВВОД если второе число перед кареткой указывает в последнюю ячейку памяти
    if m[pos] == 65535: m[m[pos+1]] = stdin()

    #ВЫВОД если число перед кареткой указывает в последнюю ячейку памяти
    elif m[pos+1] == 65535: stdout(m[m[pos]])

    #SUB-L-EQ
    else:
        sub = m[m[pos+1]] -  m[m[pos]]
        if sub < 0: sub+=65536
        
        m[m[pos+1]] = sub
        
        #Less or EQual
        if sub == 0 or not sub < 32768: pos = m[pos+2]-3

    #По умолчанию каретка постоянно едет вперёд
    pos+=3

Вы можете справедливо заметить, что я нарочно делаю повторные итерации по ленте (вызовы вида m[m[pos+1]] - m[m[pos]]), что колоссально бьёт по производительности (особенно в Python, где списки являются динамическими массивами), однако это опять же задел на будущее. Что бы мы делали, если бы у нас не было такого мощного инструментария, как Python, а был бы… другой стековый калькулятор?

m = [0] * 65536

i = 0
for image in sys.argv[1:]:
    with open(image) as f:
        for line in f.readlines():
            for v in line.split():
                m[i] = int(v)
                if m[i] < 0: m[i] = 65535 + m[i] + 1
                i = i + 1

stdin = lambda: ord(sys.stdin.read(1))

stdout = lambda c: print(chr(c), end="", flush=True)

pos = 0
while 1:
    if m[pos] == 65535: m[m[pos+1]] = stdin()

    elif m[pos+1] == 65535: stdout(m[m[pos]])
        
    else:
        sub = m[m[pos+1]] -  m[m[pos]]
        if sub < 0: sub+=65536
        
        m[m[pos+1]] = sub
        
        if sub == 0 or not sub < 32768: pos = m[pos+2]-3
        
    pos+=3

Тестируем Forth

Теперь мы можем честно открывать консоль и запускать ядро Форта на нашем процессоре. Работает оно очень и очень медленно, однако это совершенно не важно)

Попробуем ознакомиться со списком слов данной реализации Forth. Пишем слово words.

cold editor quit load evaluate set-input get-input list blank block buffer empty-buffers flush save-buffers update b/buf at-xy page bell ms [if] [else] [then] defined dump see compile-only immediate postpone  .( ( abort" $" ." exit rdrop r> >r marker does> >body user constant variable create next aft for else repeat while then again until if begin recurse ' :noname : ; [char] char word definitions +order -order (order) get-order interpret compile, literal compile find search-wordlist cfa nfa compare .s number? >number . u. u.r sign <# #s # #> hold parse -trailing query tib expect accept echo / mod /mod m/mod um/mod * um* d+ dnegate um+ abort throw catch space erase fill cmove type +string count c, , allot align aligned source 2r> 2>r 2@ 2! source-id min max c! c@ lshift +! pick set-current get-current cr emit key key? ?exit execute cell- cells cell+ cell abs s>d negate within u<= u>= u> u< <= >= 0>= 0< > < 0<= 0<> 0> <> = 2dup 2drop -rot rot r@ ?dup tuck nip [ ] decimal hex rp! rp@ sp! sp@ here bl span >in state hld dpl base scr blk context #vocs pad this root-voc current <ok> ! @ 2/ and or xor invert over ) 1- 1+ 2* 0= rshift swap drop dup bye - + eforth words only forth system forth-wordlist set-order  ok

Как я уже упоминал выше, конкретно наша спецификация называется eForth. Её придумал в 2000-х годах некий Bill Muench, ссылку на которого уже не так просто найти (эта кидает в 404 на проданном хостинге). Сам он писал, что описал эту спецификацию, так как «хотел получить полноценную систему на Форте, которая бы легко развёртывалась где угодно и содержала простые 30 слов для низкоуровневого программирования в обход ассемблеров».

Позже его дело продолжил Dr. Chen-Hanson Ting, который портировал eForth на множество платформ и мейнтейнил этот проект до самого своего ухода. eForth лишь отчасти совместим с другим амбассадором зоопарка его реализаций — Gforth (часть проекта GNU, даже небольшая страница на Википедии имеется). Это означает, что не каждый .fth-файл может корректно исполнить тот или иной интерпретатор Форта. В общем, без предварительных знаний базовых приёмов на Форт-ОС я бы вряд ли выжил…

Притча о том, как eForth создавал камни в своём огороде

Одно из наиболее ярких его отличий от других реализаций — полное отсутствие конструкции DO-..-LOOP, которую вы, вероятнее всего, будете видеть практически в каждом введении в синтаксис Форта. В eForth же от неё сознательно отказались в пользу другой, совершенно противоположенной базовой конструкции FOR-..-NEXT.

Вы можете ввести : sum ( n -- ) for + next ; в консоль Forth и увидеть это:

Помутнение рассудка после получения подобных результатов — это нормально, не волнуйтесь. Дело в том, что у eForth-сектантов свой взгляд на нумерацию элементов и индексы (см. эту ману).

Кстати, он был реализован ещё и на JavaScript, что позволяет мне нагло встроить прямо тут oembed-ссылку на Codepen с этим интерпретатором:

Может работать криво на мобильном

Теперь вы можете попрактиковаться в пользовании этой прекрасной и универсальной системой самостоятельно. Я же приведу несколько примеров с подробным разбором слов, используемых в них — просто чтобы вы могли прочувствовать разработку под ней.

В первую очередь нужно разобраться с обратной связью интерпретатора — пишем что-либо странное, что наверняка отсутствует в словаре.

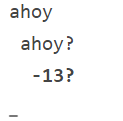
Что за -13? Ладно, думаю, и так очевидно, что это реализация кодов ошибок.

Тут я попытался напечатать несуществующий элемент стека и выполнить деление на 0. В общем, всё работает достаточно стабильно.

Теперь попробуем определить своё слово. Для этого нам понадобиться встроенное слово :.

После его активации, все дальнейшие слова кроме ; будут добавляться в определение нашего нового слова. ; же прекратит этот процесс и вернёт управление основному потоку. Важно понимать, что переносы строк вообще ничего для Forth не значат. Вся программа может быть записана в одну строку, путём простого удаления всех включений n из исходного файла.

Если вы хотите преисполниться и написать на Форте какой-нибудь готовый скрипт, взаимодействующий с пользователем, то этих знаний определённо будет мало. Могу посоветовать вам эти статьи на русском (1, 2) и оригинальную спецификацию (ссылка на PDF) от Dr Ting соответственно.

Я же, в свою очередь, ещё не покрыл свою месячную квоту на эзотерику, так что мы переходим к нашему следующему пациенту.

Piet

Далее в нашем тематическом меню на сегодня идёт, вероятно, один из самых попсовых «странных языков программирования». Моим любимым примером для демонстрации его философии является эта исчерпывающая картинка:

Работает эта программа буквально в пару шагов, однако для её понимания нам в любом случае придётся обратиться к esolangs (удивительным образом, Piet удостоился даже разбора синтаксиса на Википедии). Больше забавных картинок можно найти на этой странице.

Теперь предлагаю и вам погрузиться в этот концептуальный язык. И нет, в Piet у того или иного цвета нет конкретной функции. Функции (они же операции над стеком) появляются на стыках разных цветов — т.е. они относительны для каждой пары соседних пикселей разного цвета.

Выполнение программы осуществляет курсор (наподобие черепашки), который по умолчанию едет вперёд и вправо, если упёрся в тупик. Чёрные пиксели — стены. Белые — пустота, на стыке с которой у цветов нет функций.

Для наглядной демонстрации относительных функций цветов я сделал снимок палитры в трёх разных состояниях: с текущим выбранным розовым, красным и жёлтым цветом. Названия функций в клетках обозначают, что если курсор из пикселя текущего цвета на рисунке попадёт в другой цвет из палитры, то выполнится указанная функция. Вполне логично, что у текущего выбранного цвета относительно себя нет функции — он может означать вообще любую команду в зависимости от того, какой цвет ему предшествовал.

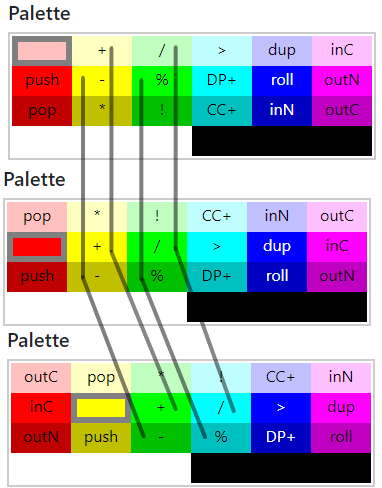
Примерно таким образом и выглядит таблица функций данного языка. Осталось разобраться ещё с парой особенностей. Во-первых, если следующий пиксель на пути курсора того же цвета, что и текущий, то курсор просто телепортируется вперёд по этой дорожке из одинаковых пикселей, пока не дойдёт до тупика или другого цвета. При этом количество пикселей в этой дорожке добавляется во встроенный регистр курсора и может быть добавлено в стек командой push. Именно так и работает поиск числа пи: сначала в стек добавляется радиус (площадь тонкой красной дорожки в начале программы), потом курсор телепортируется через этот гигантский круг, добавляя его площадь в стек аналогичным образом.

Начиная играться с Piet, стоит обратить внимание и на простоту его запуска. Вы можете просто перейти на piet.bubbler.one и редактировать/тестировать рисунки прямо на вашем JavaScript. Следовательно, демонстрации тех или иных скриптов я тоже могу вам показывать в интерактивном формате codepen:

Debug-Start-RunSpeed=10-Run

Надеюсь, вам удалось запустить картинку с обложки статьи. Теперь язык нас официально поприветствовал, так давайте же ответим ему взаимностью:

Компиляция ядра

Если внимательно присмотреться к последним нескольким командам, то приходит высшее осознание могущества сия интерпретатора. Мы можем доставать произвольный элемент стека при помощи Roll и засовывать его на место им же — это и будет наш способ взаимодействия с памятью, пусть и весьма вычислительно затратный. В общем, очевидно, что для начала нам нужно загрузить Forth-ядро в стек Piet. Для этого нам просто необходимо его предварительно закодировать в изображение. Числа можно кодировать банальными столбиками одного цвета вроде этого:

К сожалению, число 65536 таким образом сохранить будет очень и очень накладно. Ядро будет разрешением минимум 65536*6000 (более 0.5 млрд пикселей).

Нужно придумать свой способ кодировки чисел в пиксели и сделать его максимально эффективным. Первое, что приходит в голову — разложение на множители. Оно легко проворачивается в обратную сторону в среде Piet (просто mul много раз) и очевидным способом выполняется заранее на всём ядре при помощи того же Python.

Да, оно позволяет немного оптимизировать колонки огромной длины, однако не является универсальным решением. К примеру, число 65521 является простым и останется в неизменном виде. Так ещё и перед разложением нужно хранить мета-число, указывающее на количество чисел для сборки (что-бы вовремя остановиться и перейти к следующему числу).

Дальше я подумал — а почему бы не раскладывать на небольшие числа (2,3,5) и остатки от деления на каждом шагу? Например, 41 = 5*(3*3)+1. Получается математическое выражение, длина которого логарифмически зависит от изначального числа, а вот ширина (в пикселях Piet) всегда фиксирована. Такую структуру уже можно уложить змейкой на картинке и сэкономить очень много памяти за счёт логарифма. Вот только найти оптимальное разложение при начальной генерации не так просто (их может быть несколько).

Одногруппник мне на просьбу помочь с сей странной задачей открестился, мол ты алгомен и занимаешься вообще не тем, чем стоило бы.

Оптимальное решение же всё время лежало на поверхности — двоичный вид числа и есть оптимальное разложение на остатки (разложение по основанию 3 может дать небольшой прирост, однако не в нашем с вами случае; колонки высотой 2 банально неэффективно хранить в сравнении с одиночными пикселями).

Другими словами, запускаем этот высокотехнологичный код на Python:

bin(65521)[2:]     #'1111111111110001'

Получаем двоичное разложение числа 65521 (кто бы мог подумать...).

Вот только именно оно и является стратегией по сборке изначального листа при помощи двух атомарных действий: умножения на 2 и добавления 1. Это весьма очевидно даже по способу перевода между системами счисления — см. информатикe за 4 класс.

"0"+bin(65521)[2:].translate({ord("0"):" 2 *",ord("1"):" 2 * 1 +"})    # '0 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 1 + 2 * 2 * 2 * 2 * 1 +'
"0"+bin(65536)[2:].translate({ord("0"):" 2 *",ord("1"):" 2 * 1 +"})    # '0 2 * 1 + 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 *'
#Честно, я до сих пор не понимаю - почему string.translate реализовано настолько топорно и совершенно никак не Python way'ем. Если в Python 2, где было криво всё, что связано с таблицами символов, ещё можно было понять эти ord для "таблицы перевода", то сейчас они выглядят исключительно странно, см. https://stackoverflow.com/questions/21038891/what-does-table-in-the-string-translate-function-mean.
#Можно заметить, что первое умножение на 2 бывает вырожденное (2*0)
#Выполним оптимизации постфактум при помощи strip:
"1 "+bin(4)[2:].translate({ord("0"):" 2 *",ord("1"):" 2 * 1 +"}).lstrip(" 2 *").lstrip(" 1 +")    # '1 2 * 2 *'

Как вы уже могли заметить, мы превратили наше гигантское число в небольшую последовательность арифметических действий для… стекового калькулятора!

И действительно, если последовательно выполнять эти действия, то мы получим изначальное число как раз за количество операций порядка 2-го логарифма.

Проверить это мы можем и в том же Forth, промотав статью чуть выше до его консоли.

Рисуем процессор

Пока что не будем превращать ядро в изображение — Python с PIL от нас никуда не убегут. Предлагаю теперь заняться наиболее сложным и долгим элементом с точки зрения реализации — самим subleq-процессором. Для загрузки ядра в Piet извне я пока что буду использовать вот такой стенд:

Это что-то вроде реализации цикла for. Первым числом в stdin подаётся количество элементов, а дальше в стек добавляются всё новые и новыё числа (счётчик при этом всплывает наверх при помощи roll). Когда счётчик падает до конца, то розовый пиксель с инструкцией DP+ отпускает каретку направо.

IN(NUM)  # количество грядущих элементов
IN(NUM)  # :(начало)
PUSH 2   # аргументы для roll
PUSH 1
ROLL     # подъём счетчика из под нового числа (что бы он оказался на вершине)
DUP   # бэкап счетчика, ведь сравнение его поглотит
PUSH 1
-
PUSH 1
>            # сравнение счётчика-1 с 1
POINTER # поворот в :(начало)

Предположим, что мы уже смогли загрузить ядро Forth в стек Piet. Пусть полный стек на данный момент выглядит так: E D C B A 0 <- — на вершине находится стартовый индекс каретки (pos).

Далее мы должны попадать в некий замкнутый маршрут на рисунке, где последовательно будут выполняться следующие действия:

1. Подъём новой тройки элементов из заданной позиции на вершину стека (при помощи roll).
2. Полное копирование всех трёх элементов тройки (несколько roll и dup).
3. Возвращение тройки на место в стеке (чтобы выполнить фактическое копирование и получить на вершине наши заветные три числа для subleq).
4. Выполнение инструкции над числами и внесение изменений в стек при необходимости

Конечно, я не затрагиваю необходимость постоянно совершать лишние roll/dup, ведь каждый roll/greater/sum и т. п. при выполнении безвозвратно поглощают верхнюю пару элементов в качестве своих аргументов.

Фактически, самыми сложным пунктом является именно копирование тройки элементов из ядра, ведь dup нужно поочерёдно применить на каждый элемент, так ещё и вернуть оригинальные обратно на место (для этого нужно ещё и всё это время сохранять pos где-то неподалёку).

Казалось бы — просто копирование, чего тут сложного? Вот только без переменных и какого-либо инструментария взаимодействия с кусками стека, кроме roll, эта простая операция превращается в настоящую пытку. Весь процесс похож скорее на занудное и безумно вычислительно затратное жонглирование элементами стека, в попытках расставить их в правильном порядке для дальнейшего применения других операций.

Возможно, я просто недостаточно глубоко отказался от концепций вроде переменных…

По очевидным причинам я не стану рассказывать о предназначении каждого пикселя (скорее всего, я и сам уже с первого взгляда не пойму, что делает тот или иной блок). Конкретику вам может поведать дебаггер, я же ограничусь общими комментариями.

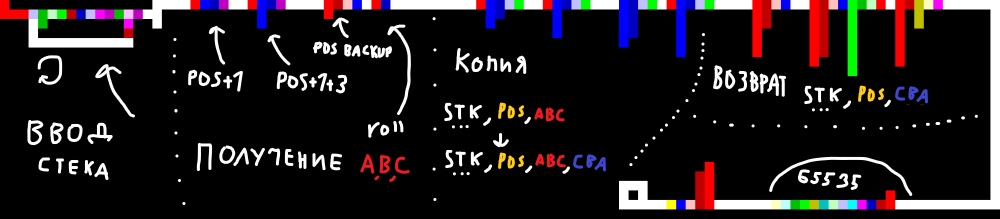
Ссылка на интерактивную версию. Можете попробовать что-то вроде 11 9 8 7 6 5 4 3 2 1 4, где первый элемент — количество данных для ввода +1, а последний — pos.

Казалось бы, такая простая программа, а сколько времени и внимания приходится потратить на создание подобной — просто жуть. Мне по пути пришло осознание того, что даже операцию equal в этот язык не завезли. Вот хоть убейся, а без тёмных ритуалов два числа не сравнить…

Внизу схемы я оставляю заготовку для выполнения самой операции subleq — создаю число 65536-1 (т. е. -1 в uint16). Его можно максимально быстро получить без всяких издержек как 2 - 4 - 16 - 256 - 65536 — просто четыре раза сделать DUP и MUL.

Далее остаётся сравнить c этим числом A и B (для проверки на необходимость ввода/вывода) и изменить POS на C, если результат меньше нуля. После этого можно возвращаться по дорожке из белых пикселей к началу схемы и выполнять нашу функцию над памятью повторно. В каком-то смысле такая архитектура даже более атомарна, чем оригинальная машина тьюринга — она не хранит состояния в регистрах, а держит всё и сразу на ленте. Таким образом, сохранив текущий стек, мы сделаем полную копию состояния нашей машины. Это приближает нас к идее Фон-Неймана (её я намеренно пропустил во введении, ведь она явно не отражается в нашем сегодняшнем мини-проекте).

Вы уже могли заметить, что я пропустил одну важную деталь. Если быть точнее, то я её намеренно умолчал. Заключается она в том, что даже максимально эффективно свернув наше ядро, мы всё равно получим Piet-программу, которая будет инициализироваться со скоростью 100 пикс/сек более 30 минут (и это по самому оптимистичному прогнозу). Такие жуткие числа по факту не оставляют шанса на какой-либо дебаг или тестирование всей архитектуры воедино.
Однако нельзя так безосновательно взять и бросить наш мысленный эксперимент — необходимо хотя бы скомпилировать ядро. Сама идея перевода любого числа в стековые операции мной уже была обозначена. Теперь соберём её в полноценную функцию с обработкой крайних значений:

def toforth(num):
    if num == 0:return "1 1 -"
    if num == -1:num=65535
    return "1 "+bin(num)[2:].translate({ord("0"):" 2 *",ord("1"):" 2 * 1 +"}).lstrip(" 2 *").lstrip(" 1 +")

Проверим, что всё работает корректно:

def test_toforth():
    assert toforth(3)=="1 2 * 1 +"
    assert toforth(4)=="1 2 * 2 *"

Оставим это на совести pytest и перейдём к более насущной задаче — переводу нашего Forth-кода в Piet. Для начала напишем функцию, которая превращает текстовую команду в относительный сдвиг по палитре Piet. В cur_col изначально лежат координаты вида [0,0], функция принимает указатель на него. В данной таблице можно найти соответствия вида "операция" = [сдвиг тона, сдвиг яркости], эти сдвиги мы и будем применять к текущему цвету для выражения операций:

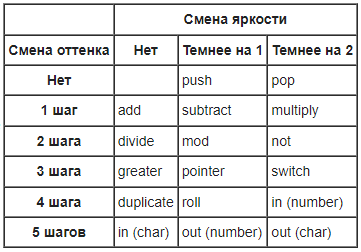
cur_col=[0,0]
def topiet(cur_col,op="+"):
    if op=="+": cur_col[0]+=1
    if op=="*":
        cur_col[0]+=1
        cur_col[1]+=2      # Изменяем тон и яркость следуя табличке
    if op=="-":
        cur_col[0]+=1
        cur_col[1]+=1
    if op=="psh":
        cur_col[1]+=1
    if cur_col[1]>2:cur_col[1]-=3
    if cur_col[0]>5:cur_col[0]-=6

Генерируем массив координат в системе Piet-палитры, учитывая взаимосвязи между цветами:

    s=toforth(65521)
    cur_col=[0,0]
    cols=[]
    cols.append(cur_col.copy())
    for i in s.split(" "):
        if i=="1":
            topiet(cur_col,"psh")
        elif i=="2":
            e=cols.pop(-1).copy()
            cols+=[e]*2
            topiet(cur_col,"psh")
        elif i=="+":
            topiet(cur_col,"+")
        elif i=="-":
            topiet(cur_col,"-")
        elif i=="*":
            topiet(cur_col,"*")
            
        cols.append(cur_col.copy())

Теперь мы имеем массив абсолютных координат палитры. Каждый элемент в нём соответствует конкретному пикселю, а комплексные команды вроде PUSH 2 уже преобразованы в двойные пиксели.

Остаётся только преобразовать координаты палитры в цвета и сгенерировать изображение.

pixels=[]
#Палитра Piet в HEX (взята с Википедии)
mat=[["#FFC0C0","#FFFFC0","#C0FFC0","#C0FFFF","#C0C0FF","#FFC0FF"],
["#FF0000","#FFFF00","#00FF00","#00FFFF","#0000FF","#FF00FF"],
["#C00000","#C0C000","#00C000","#00C0C0","#0000C0","#C000C0"]]

from PIL import ImageColor

#Переводим HEX в RGB
for i in cols: pixels.append(ImageColor.getcolor(mat[i[1]][i[0]], "RGB"))
pixels.append(ImageColor.getcolor("#FFFFFF", "RGB"))
#Конец числа обозначен пикселем без функции

Отлично! Мы получили массив pixels, который уже полностью готов к употреблению. Он содержит готовые RGB-сеты и может быть напрямую записан в объект Image модуля PIL.

from PIL import Image
img = Image.new('RGB', [len(pixels),1], 255)
data = img.load()

for i in range(len(pixels)):
    data[i,0]=pixels[i]
img.save('image.png')

Вот так выглядит число 55 в закодированном виде:

А вот так выглядят 2 подряд идущие числа 16:

Подобные ленты уже можно смело загружать в Piet и получать изначальный закодированный стек. Интерактивная демонстрация, которая собирает числа 65521,0,17 в стеке:

На этом моменте я и хотел бы закончить свое повествование. Ядро содержит в себе 6000 чисел, в то же время мой PIL завис уже после первых 1500 чисел (картинка около 10к пикселей в ширину). И нет, ситуация вовсе не тупиковая, просто я не смогу вам как-либо передать изображение в разрешении 40к, тем более вы не сможете его где-либо запустить.

Заключение

Не думаю, что из всего вышесказанного можно выжать хоть какой-то намёк на вывод. Применимо ли это в реальной жизни? Однозначно нет. Конечно, найдутся и те, кто будут с пеной у рта доказывать, что они запустили Forth на Arduino и теперь у них якобы есть удобная и минималистичная платформа — на вкус и цвет, как говорится...

Крут ли Piet? Думаю, да. Пусть код на нём и является write-only (без дебаггера вы не сможете прочитать программу), но действительно ли это критично? Большинство регулярных выражений в реальной жизни тоже едва ли читаемы. Пусть он и заезжен научпопом как «the most weird programming language», однако после Форта он уже и не так специфичен…

Почему же он крут? Да потому что когда твоя спиралька из пикселей начинает реально работать и выполнять задачу, ты, как её создатель, испытываешь невероятный экстаз. В конце концов, многие идейные программисты — это не успешные предприниматели на пляже маями, а разочарованные в индустрии свидетели церкви cobol'a, возможно, ещё и повёрнутые на эзотерике.

Дух Форта при этом жив ещё и в академических экспериментах вроде Joy и Kitten, ведь уникальные концепции всегда притягивают пытливые умы. Подобные инкарнации при этом пусть и не способны оказать влияния на индустрию, однако могут эффектно демонстрировать эзотерические идеи в обёртке современного Python-подобного синтаксиса.

Об этом всем можно было бы поговорить ещё, однако этот текст и так уже затянулся. Если найдётся аудитория, которой этот материал приглянется, то собрать углублённого контента на вторую часть не составит труда, однако конкретно эту статью стоит подвести к концу.

Если вы действительно дошли до этого момента, то я могу лишь поблагодарить вас за уделённое чтению время.