Кластеризация в ML: от теоретических основ популярных алгоритмов к их реализации с нуля на Python

Кластеризация — это набор методов без учителя для группировки данных по определённым критериям в так называемые кластеры, что позволяет выявлять сходства и различия между объектами, а также упрощать их анализ и визуализацию. Из-за частичного сходства в постановке задач с классификацией кластеризацию ещё называют unsupervised classification.

В данной статье описан не только принцип работы популярных алгоритмов кластеризации от простых к более продвинутым, но а также представлены их упрощённые реализации с нуля на Python, отражающие основную идею. Помимо этого, в конце каждого раздела указаны дополнительные источники для более глубокого ознакомления.

Ноутбук с данными алгоритмами можно загрузить на Kaggle (eng) и GitHub (rus).

Содержание

• Области применения кластеризации и её разновидности

• К-средних

• Агломеративная кластеризация

• Спектральная кластеризация

• DBSCAN

• Affinity Propagation

Области применения кластеризации и её разновидности

Кластеризация широко применяется в машинном обучении для решения различного спектра задач:

• классификация (определение к какому классу относится каждый объект или же выделение новых классов, которые не были известны заранее);

• сегментация рынка (разделение потенциальных клиентов на группы по их характеристикам для разработки более эффективных стратегий в маркетинге и продажах);

• сегментация изображений (разделение изображения на сегменты или группы пикселей);

• кластеризация геоданных (группировка данных по их географическому расположению, например, разделение районов на безопасные и опасные, богатые и бедные, и так далее);

• понижение размерности (уменьшение количества признаков путем объединения схожих в один кластер).

Существует множество различных типов кластеризации, которые можно разделить по следующим критериям:

• По способу формирования кластеров:

  • Разделительные (partitioning) — разбивают данные на заданное число кластеров, минимизируя расстояние внутри кластера и максимизируя расстояние между кластерами (например, K-means).

  • Основанные на плотности (density-based) — группируют точки, которые находятся в областях с высокой плотностью и отделяют их от областей с низкой плотностью (например, DBSCAN).

  • Основанные на сетке (grid-based) — разбивают пространство на ячейки сетки и анализируют плотность данных в каждой ячейке (например, STING).

  • Основанные на модели (model-based) — предполагают, что данные порождены некоторой статистической моделью и пытаются подобрать параметры этой модели (например, смеси Гауссианов).

  • Основанные на графах (graph-based) — используют графовое представление данных и разбивают его на подграфы, соответствующие кластерам (например, спектральная кластеризация).

  • Основанные на подпространствах (subspace-based) — ищут кластеры в подпространствах признаков, а не во всём пространстве (например, CLIQUE).

  • Основанные на ансамбле (ensemble-based) — комбинируют результаты различных алгоритмов кластеризации, чтобы получить более стабильное и надёжное разбиение (например, CSPA).

• По степени вложенности кластеров:

  • Плоские (flat) — разбивают данные на один уровень кластеров, не учитывая их иерархию (например, K-means).

  • Иерархические (hierarchical) — разбивают данные на несколько уровней кластеров, учитывая их иерархию. Существуют два основных подхода к иерархической кластеризации: агломеративный (начинается с того, что каждый объект является отдельным кластером, а затем постепенно наиболее близкие кластеры объединяются в более крупные) и дивизивный (начинается с того, что все объекты составляют один кластер, а затем постепенно разделяются на более мелкие кластеры).

• По степени пересечения кластеров:

  • Исключающие (exclusive) — каждый объект принадлежит только одному кластеру (например, K-means).

  • Перекрывающие (overlapping) — каждый объект может принадлежать нескольким кластерам (например, MCOKE).

  • Нечёткие (fuzzy) — каждый объект принадлежит каждому кластеру с некоторой степенью принадлежности (например, fuzzy K-means).

---

K-Means

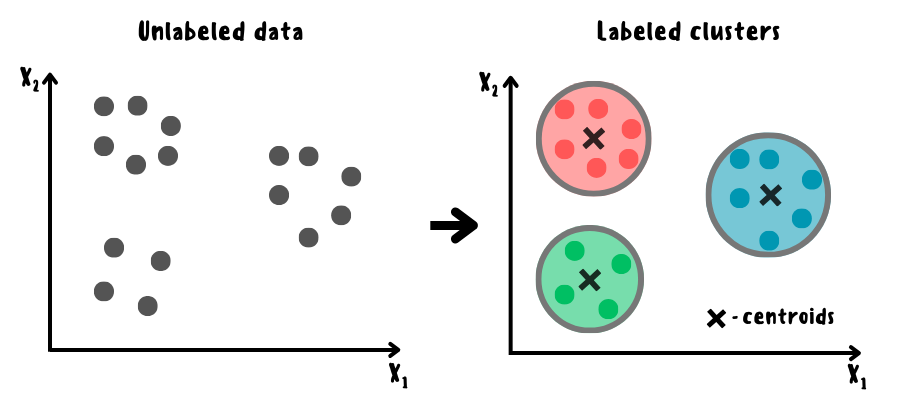
Кластеризация K-средних представляет собой одну из самых простых реализаций, суть которой заключается в итеративной инициализации центроидов для каждого кластера на основе среднего арифметического расположенных в нём наблюдений, а также их переопределении путём минимизации суммарного квадратичного отклонения от центроидов кластеров.

Существуют различные вариации алгоритма K-Means, которые модифицируют его шаги или функцию потерь для улучшения производительности, а также применимости к разным типам данных. К самым популярным вариациям относятся следующие:

• Lloyd's algorithm — это классический вариант K-Means, который хорошо работает для сферических кластеров с одинаковой плотностью, но может давать плохие результаты для других форм или размеров кластеров.

• Elkan algorithm — более быстрый вариант классического K-Means, который использует неравенство треугольника для уменьшения количества вычислений расстояний между объектами и центроидами, что может быть эффективнее на некоторых наборах данных с хорошо определёнными кластерами, однако требуется больше памяти из-за выделения дополнительного массива размера (n_samples, n_clusters).

• Mini-batch K-Means — модификация классического K-Means, использующая случайные подвыборки данных на каждой итерации для обучения. Хорошо подходит для больших датасетов.

• K-Medoids — вариант K-Means, который в качестве центроидов выбирает реальные точки (медоиды) из данных, а не их средние значения, что повышает устойчивость к выбросам.

• K-Modes — вариант алгоритма K-Means для работы с категориальными данными, который выбирает один из объектов в кластере в качестве моды и минимизирует сумму расстояний Хэмминга между модой и объектами в кластере. Расстояние Хэмминга представляет из себя количество позиций, в которых значения векторов не совпадают.

Одним из ключевых вопросов при использовании K-Means является выбор начальных центроидов, поскольку от них зависит качество и скорость сходимости алгоритма. Существует несколько способов инициализации центроидов:

• Случайный выбор: выбирается k случайных точек из данных в качестве начальных центроидов. Такой метод прост, но может привести к плохим результатам, если начальные центроиды слишком близки друг к другу или к краям распределения.

• K-Means++: первый центроид выбирается случайно, а затем выбираются остальные центроиды с вероятностью, пропорциональной квадрату расстояния до ближайшего уже выбранного центроида. Данный метод улучшает качество кластеризации, уменьшая вероятность попадания в локальный минимум, но требует дополнительных вычислений.

• Greedy K-Means++ — модификация K-Means++, которая ускоряет сходимость и улучшает качество кластеризации за счёт того, что на каждом шаге при выборе центра кластера производится несколько попыток и выбирается лучший (тот, который минимизирует суммарное квадратичное отклонение точек от центров кластеров).

Другим важным аспектом, влияющим на качество алгоритма, является подбор оптимального числа кластеров k, которое устанавливается заранее вручную. Существует несколько методов для выбора оптимального k:

• Метод локтя, основанный на графике суммы квадратов расстояний между объектами и центроидами кластеров (SSE) в зависимости от k. Оптимальным k считается та точка, после которой SSE уменьшается незначительно.

• Метод силуэта, основанный на графике среднего значения силуэта для каждого k. Силуэт — это мера того, насколько хорошо объект отнесён к своему кластеру по сравнению с другими кластерами. Оптимальным k считается та точка, где силуэт достигает максимума.

• Метод комплексной оценки, основанный на анализе нескольких критериев, таких как динамика перераспределения объектов в кластерах, изменение потенциальной энергии объектов внутри кластеров и характерные точки графиков этих критериев. Оптимальным k считается точка, которая удовлетворяет набору правил, использующих данные критерии.

Принцип работы Lloyd's K-Means с инициализацией Greedy K-Means++

Алгоритм строится следующим образом:

• 1) изначально вычисляются центроиды кластеров с помощью алгоритма Greedy K-Means++;

• 2) далее рассчитывается квадрат евклидова (или другого) расстояния от каждого наблюдения до центроидов;

• 3) на основе полученного расстояния наблюдениям присваиваются метки кластеров, которые к ним расположены ближе всего, а также рассчитывается инерция — мера того, насколько хорошо данные были разбиты на кластеры;

• 4) шаги 2-3 повторяются до тех пор, пока инерция на текущей и предыдущей итерациях перестанет изменяться меньше установленного порога (пока положение центроидов перестанет изменяться в пространстве) или пока не будет достигнуто установленное количество итераций;

• 5) Наблюдения, расположенные ближе всего к полученным центроидам, и будут составлять кластеры.

Принцип работы алгоритма Greedy K-Means++:

• 1) первый центроид выбирается случайным образом из данных;

• 2) для каждого следующего центроида выбирается точка в данных с вероятностью, пропорциональной квадрату расстояния до ближайшего центроида среди нескольких кандидатов, выбранных случайным образом;

• 3) данный процесс повторяется пока не будет выбрано установленное количество центроидов.

Импорт необходимых библиотек

import numpy as np
from scipy.spatial.distance import cdist
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.metrics import adjusted_rand_score
from sklearn.cluster import KMeans

Реализация на Python с нуля

class KMeansClustering:
    def __init__(self, n_clusters=8, max_iter=300, tol=0.0001, random_state=0):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.tol = tol
        self.random_state = random_state

    def _greedy_kmeans_plus_plus(self, X):
        np.random.seed(self.random_state)
        n_samples, n_features = X.shape
        n_local_trials = 2 + int(np.log(self.n_clusters))

        indices = np.arange(n_samples)
        first_index = np.random.choice(indices)
        centers = np.zeros((self.n_clusters, n_features))

        centers[0] = X[first_index]
        first_center = centers[0].reshape(1, -1)
        sq_distances = cdist(X, first_center, metric='sqeuclidean').ravel()

        for i in range(1, self.n_clusters):
            min_cost = np.inf
            min_new_sq_distances = []
            best_candidate_index = None

            for _ in range(n_local_trials):
                candidates_probas = sq_distances / np.sum(sq_distances)
                candidate_index = np.random.choice(indices, p=candidates_probas)
                candidate = X[candidate_index].reshape(1, -1)

                new_sq_distances = cdist(X, candidate, metric='sqeuclidean').ravel()
                new_cost = np.sum(np.minimum(sq_distances, new_sq_distances))

                if new_cost < min_cost:
                    best_candidate_index = candidate_index
                    min_new_sq_distances = new_sq_distances
                    min_cost = new_cost

            centers[i] = X[best_candidate_index]   # Choose the new center
            sq_distances = np.minimum(sq_distances, min_new_sq_distances)

        return centers

    def fit(self, X):
        n_samples, n_features = X.shape
        self.inertia_ = np.inf
        self.cluster_centers_ = self._greedy_kmeans_plus_plus(X)

        # Lloyd's algorithm
        for _ in range(self.max_iter):
            distances = cdist(X, self.cluster_centers_, metric='sqeuclidean')
            labels = np.argmin(distances, axis=1)
            new_inertia = np.sum(np.min(distances, axis=1))
            new_centers = np.zeros((self.n_clusters, n_features))

            for k in range(self.n_clusters):
                new_centers[k] = np.mean(X[labels == k], axis=0)

            if np.abs(new_inertia - self.inertia_) < self.tol:
                break

            self.inertia_ = new_inertia
            self.cluster_centers_ = new_centers

    def predict(self, X):
        distances = cdist(X, self.cluster_centers_, metric='sqeuclidean')
        predicted_labels = np.argmin(distances, axis=1)

        return predicted_labels

Загрузка датасета

X1, y1 = make_blobs(n_samples=250, n_features=2, centers=8, random_state=0)
print(y1)


[1 3 7 7 6 7 1 3 7 7 0 3 1 1 3 3 5 1 7 4 0 1 1 3 4 7 0 0 6 7 0 0 5 5 7 2 1
 1 6 5 4 7 1 2 1 1 4 3 6 4 7 3 0 2 2 1 7 2 4 0 0 0 1 4 6 5 0 4 6 6 4 4 1 4
 2 3 1 1 5 4 6 4 1 2 5 0 7 6 7 3 0 1 2 5 1 5 3 3 3 1 5 4 0 4 7 6 2 2 2 4 6
 2 5 1 6 4 0 6 5 0 0 6 3 5 1 6 0 2 5 5 6 3 3 1 5 4 5 0 2 2 3 0 4 7 5 4 2 0
 2 6 2 5 2 1 4 1 5 0 4 6 7 5 5 7 6 2 2 3 6 1 7 3 4 7 2 6 6 4 2 2 0 5 4 4 6
 3 1 7 6 7 7 0 4 5 7 2 6 6 2 5 3 3 2 7 1 7 6 6 4 3 5 7 6 3 5 0 3 3 5 5 2 0
 6 3 4 0 5 3 5 2 0 6 4 0 1 1 2 2 0 1 3 7 0 7 0 3 4 7 3 7]

Обучение моделей и оценка полученных результатов

Как можно заметить, K-Means дал достаточно хорошую, но не идеальную кластеризацию данных, что обусловлено наличием небольшого числа выбросов и более сложной формой некоторых кластеров, чем сферическая.

KMeans

kmeans = KMeansClustering(n_clusters=8, random_state=0)
kmeans.fit(X1)
kmeans_pred_res = kmeans.predict(X1)
kmeans_ari = adjusted_rand_score(y1, kmeans_pred_res)
kmeans_centroinds = kmeans.cluster_centers_
print(f'Adjusted Rand Score for KMeans: {kmeans_ari}', '', sep='n')
print('centroids', kmeans_centroinds, '', sep='n')
print('prediction', kmeans_pred_res, sep='n')


Adjusted Rand Score for KMeans: 0.8082423809657193

centroids
[[ 9.20217726 -2.23709633]
 [-1.5438023   7.64224793]
 [-8.61527648 -8.32916569]
 [ 0.81231976  4.02302811]
 [-1.81106448  2.87987747]
 [ 2.3666746   1.30457024]
 [ 1.47433518  8.49698324]
 [ 5.86512606  0.19818122]]

prediction
[5 1 2 2 6 2 5 1 2 2 5 1 5 5 1 1 5 5 2 0 3 7 3 1 0 2 3 3 6 2 1 3 7 7 2 4 5
 5 6 7 0 2 5 4 5 5 0 1 6 7 2 1 3 3 4 5 2 4 0 3 3 3 5 0 6 7 3 0 6 6 0 0 5 0
 3 1 5 5 7 0 3 0 5 4 7 3 2 6 2 6 3 5 4 5 5 7 1 1 1 3 7 0 3 0 2 6 3 4 4 0 6
 4 7 5 1 0 3 6 7 3 3 6 1 7 5 6 3 4 7 7 6 1 1 5 7 0 7 3 4 4 1 3 0 2 7 0 4 3
 4 6 4 7 4 5 0 5 7 3 0 6 2 7 5 2 6 4 3 3 6 5 2 1 0 2 4 6 6 0 4 4 3 7 0 0 6
 1 5 2 6 2 2 3 0 7 2 4 6 6 4 7 1 1 4 2 5 2 6 1 0 1 5 2 6 6 7 3 1 1 7 7 4 3
 6 1 0 3 7 1 7 4 4 6 0 3 5 5 4 4 3 3 1 2 3 2 3 1 0 2 1 2]

KMeans (scikit-learn)

sk_kmeans = KMeans(n_clusters=8, n_init='auto', random_state=0)
sk_kmeans.fit(X1)
sk_kmeans_pred_res = sk_kmeans.predict(X1)
sk_kmeans_ari = adjusted_rand_score(y1, sk_kmeans_pred_res)
sk_kmeans_centroinds = sk_kmeans.cluster_centers_
print(f'Adjusted Rand Score for sk KMeans: {sk_kmeans_ari}', '', sep='n')
print(sk_kmeans_centroinds, '', sep='n')
print('prediction', sk_kmeans_pred_res, sep='n')


Adjusted Rand Score for sk KMeans: 0.8082423809657193

[[ 9.20217726 -2.23709633]
 [-1.5438023   7.64224793]
 [-8.61527648 -8.32916569]
 [ 0.81231976  4.02302811]
 [-1.81106448  2.87987747]
 [ 2.3666746   1.30457024]
 [ 1.47433518  8.49698324]
 [ 5.86512606  0.19818122]]

prediction
[5 1 2 2 6 2 5 1 2 2 5 1 5 5 1 1 5 5 2 0 3 7 3 1 0 2 3 3 6 2 1 3 7 7 2 4 5
 5 6 7 0 2 5 4 5 5 0 1 6 7 2 1 3 3 4 5 2 4 0 3 3 3 5 0 6 7 3 0 6 6 0 0 5 0
 3 1 5 5 7 0 3 0 5 4 7 3 2 6 2 6 3 5 4 5 5 7 1 1 1 3 7 0 3 0 2 6 3 4 4 0 6
 4 7 5 1 0 3 6 7 3 3 6 1 7 5 6 3 4 7 7 6 1 1 5 7 0 7 3 4 4 1 3 0 2 7 0 4 3
 4 6 4 7 4 5 0 5 7 3 0 6 2 7 5 2 6 4 3 3 6 5 2 1 0 2 4 6 6 0 4 4 3 7 0 0 6
 1 5 2 6 2 2 3 0 7 2 4 6 6 4 7 1 1 4 2 5 2 6 1 0 1 5 2 6 6 7 3 1 1 7 7 4 3
 6 1 0 3 7 1 7 4 4 6 0 3 5 5 4 4 3 3 1 2 3 2 3 1 0 2 1 2]

Визуализация прогнозов

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.subplots_adjust(wspace=0.2)
plt.scatter(X1[:, 0], X1[:, 1], c=kmeans_pred_res, cmap="rainbow")
plt.scatter(kmeans_centroinds[:, 0], kmeans_centroinds[:, 1], marker="x", color="black", s=100)
plt.title("KMeans")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

plt.subplot(1, 2, 2)
plt.subplots_adjust(wspace=0.2)
plt.scatter(X1[:, 0], X1[:, 1], c=sk_kmeans_pred_res, cmap="rainbow")
plt.scatter(sk_kmeans_centroinds[:, 0], sk_kmeans_centroinds[:, 1], marker="x", color="black", s=100)
plt.title("KMeans (scikit-learn)")
plt.xlabel("Feature 1")

plt.show()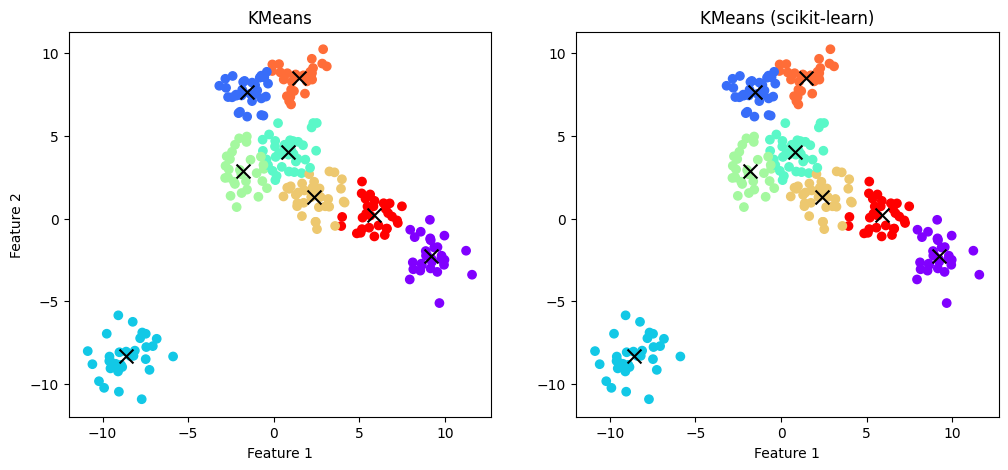

Преимущества и недостатки K-Means

Преимущества:

• прост в реализации и понимании;

• наличие большого числа модификаций;

• высокая скорость работы и точность на данных сферической формы.

Недостатки:

• низкая точность на данных с несферической формой кластеров;

• чувствительность к начальным значениям центроидов и выбросам;

• необходимость заранее устанавливать число кластеров, что может быть сложно или не оптимально.

Дополнительные источники

Статья «Improved Guarantees for k-means++ and k-means++ Parallel», Konstantin Makarychev, Aravind Reddy and Liren Shan.

Документация: описание K-Means, K-Means (алгоритм).

Видео: один, два.

---

Агломеративная кластеризация

Алгломеративная кластеризация — это метод иерархической кластеризации, который объединяет объекты в кластеры на основе их близости. Процесс кластеризации начинается с того, что изначально каждый объект считается отдельным кластером, а затем на каждом шаге два наиболее близких кластера сливаются в один, пока не будет достигнуто желаемое число кластеров или один общий кластер.

Важным аспектом в алгломеративной кластеризаци является способ вычисления расстояния между кластерами, который называется связью. Можно выделить несколько методов для вычисления связи:

• Метод одиночной связи (single linkage): расстояние между кластерами равно минимальному расстоянию между точками из разных кластеров. Этот метод склонен к созданию длинных и извилистых кластеров.

• Метод полной связи (complete linkage): расстояние между кластерами равно максимальному расстоянию между точками из разных кластеров. Этот метод склонен к созданию компактных и сферических кластеров.

• Метод средней связи (average linkage): расстояние между кластерами равно среднему расстоянию между всеми парами точек из разных кластеров. Этот метод является компромиссом между методами одиночной и полной связи.

• Метод Уорда (Ward's linkage): расстояние между кластерами равно приросту суммы квадратов расстояний от точек до центроидов кластеров при объединении этих кластеров. Этот метод стремится минимизировать внутрикластерную дисперсию.

Принцип работы агломеративной кластеризации на основе метода Уорда

Алгоритм строится следующим образом:

• 1) для каждой пары кластеров рассчитывается расстояние Уорда на основе евклидова расстояния;

• 2) метки с минимальным расстоянием, то есть ближайшие кластеры объединяются в новый следующим образом: всем объектам одного кластера присваиваются метки другого, после чего все новые метки, которые больше меток другого кластера, уменьшаются на 1, то есть их нумерация сдвигается влево для устранения пропусков в последовательности;

• 3) шаги 1-2 повторяются пока количество кластеров больше целевого n_clusters.

Импорт необходимых библиотек

import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial.distance import sqeuclidean
from scipy.cluster.hierarchy import linkage, dendrogram
from sklearn.datasets import make_blobs
from sklearn.metrics import adjusted_rand_score
from sklearn.cluster import AgglomerativeClustering

Реализация на Python с нуля

class HierarchicalAgglomerativeClustering:
    def __init__(self, n_clusters=2):
        self.n_clusters = n_clusters

    @staticmethod
    def _ward_distance(c1, c2):
        n1, n2 = len(c1), len(c2)
        c1_mean, c2_mean = np.mean(c1, axis=0), np.mean(c2, axis=0)
        sqeuclidean_dist = sqeuclidean(c1_mean, c2_mean)

        return (n1 * n2) / (n1 + n2) * sqeuclidean_dist

    @staticmethod
    def _update_labels(labels, min_cdist_idxs):
        # assign a cluster number to labels
        labels[labels == min_cdist_idxs[1]] = min_cdist_idxs[0]
        labels[labels > min_cdist_idxs[1]] -= 1

        return labels

    def fit_predict(self, X):
        labels = np.arange(len(X))
        clusters = [[x] for x in X]

        while len(clusters) > self.n_clusters:
            min_cdist, min_cdist_idxs = np.inf, []

            for i in range(len(clusters) - 1):
                for j in range(i + 1, len(clusters)):
                    cdist = self._ward_distance(clusters[i], clusters[j])

                    if cdist < min_cdist:
                        min_cdist = cdist
                        min_cdist_idxs = (i, j)

            labels = self._update_labels(labels, min_cdist_idxs)
            clusters[min_cdist_idxs[0]].extend(clusters.pop(min_cdist_idxs[1]))

        return np.array(labels)

Загрузка датасета

X2, y2 = make_blobs(n_samples=75, n_features=2, centers=5, random_state=0)
print(y2)


[0 3 4 3 2 4 0 2 0 4 2 4 2 2 0 0 0 3 2 0 2 2 2 3 4 1 1 2 3 0 4 4 3 3 3 2 2
 0 1 1 3 1 0 2 4 1 4 4 0 4 1 0 3 0 4 1 2 1 4 3 1 1 3 0 3 4 1 2 1 4 0 3 1 1
 3]

Обучение моделей и оценка полученных результатов

В данном случае агломеративная кластеризация также справилась достаточно хорошо, но при сравнении графиков можно заметить, что метки ручной реализации имеют другие значения и соответственно цвет на графике. Это связано с другим порядком формирования кластеров: в scikit-learn используется структура данных, известная как linkage tree, позволяющая визуализировать иерархию кластеров с помощью древовидной диаграммы (дендограммы), что может быть полезно при выборе оптимального количества кластеров.

Стоит отметить, что порядок формирования кластеров не влияет на качество кластеризации, поскольку сами метки кластеров разделяются правильно, что видно из одинаковых значений ARI.

AgglomerativeClustering

ac = HierarchicalAgglomerativeClustering(n_clusters=5)
ac_pred_res = ac.fit_predict(X2)
ac_ari = adjusted_rand_score(y2, ac_pred_res)
print(f'Adjusted Rand Score for AgglomerativeClustering: {ac_ari}', '', sep='n')
print('prediction', ac_pred_res, sep='n')


Adjusted Rand Score for AgglomerativeClustering: 0.8370870157432925

prediction
[0 1 2 0 3 2 0 3 0 2 3 2 3 3 0 0 0 1 3 0 3 3 0 1 2 4 4 3 1 3 2 2 1 1 1 3 3
 0 4 4 1 4 0 3 2 4 2 2 3 2 4 0 1 0 2 4 3 4 2 1 4 4 1 0 1 2 4 3 3 2 0 1 4 4
 1]

AgglomerativeClustering (scikit-learn)

sk_ac = AgglomerativeClustering(n_clusters=5, linkage='ward')
sk_ac_pred_res = sk_ac.fit_predict(X2)
sk_ac_ari = adjusted_rand_score(y2, sk_ac_pred_res)
print(f'Adjusted Rand Score for sk AgglomerativeClustering: {sk_ac_ari}', '', sep='n')
print('prediction', sk_ac_pred_res, sep='n')


Adjusted Rand Score for sk AgglomerativeClustering: 0.8370870157432925

prediction
[4 2 1 4 0 1 4 0 4 1 0 1 0 0 4 4 4 2 0 4 0 0 4 2 1 3 3 0 2 0 1 1 2 2 2 0 0
 4 3 3 2 3 4 0 1 3 1 1 0 1 3 4 2 4 1 3 0 3 1 2 3 3 2 4 2 1 3 0 0 1 4 2 3 3
 2]

Визуализация прогнозов

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.scatter(X2[:, 0], X2[:, 1], c=ac_pred_res, cmap='rainbow')
plt.title('AgglomerativeClustering')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

plt.subplot(1, 2, 2)
plt.scatter(X2[:, 0], X2[:, 1], c=sk_ac_pred_res, cmap='rainbow')
plt.title('AgglomerativeClustering (scikit-learn)')
plt.xlabel("Feature 1")

plt.show()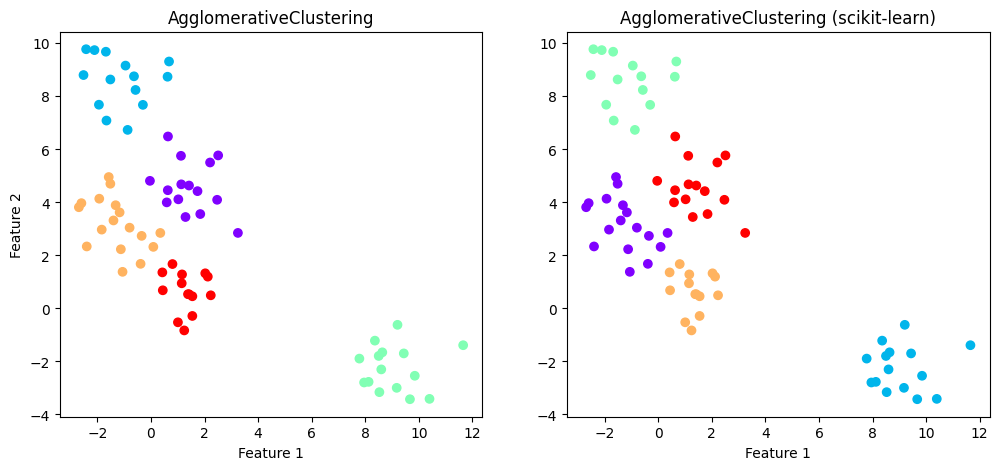

linkage_matrix = linkage(X2, method='ward', metric='euclidean')

plt.figure(figsize=(10, 6))
dendrogram(linkage_matrix, color_threshold=10)
plt.xlabel("Sample Index")
plt.ylabel("Distance")
plt.title("Dendrogram")
plt.show()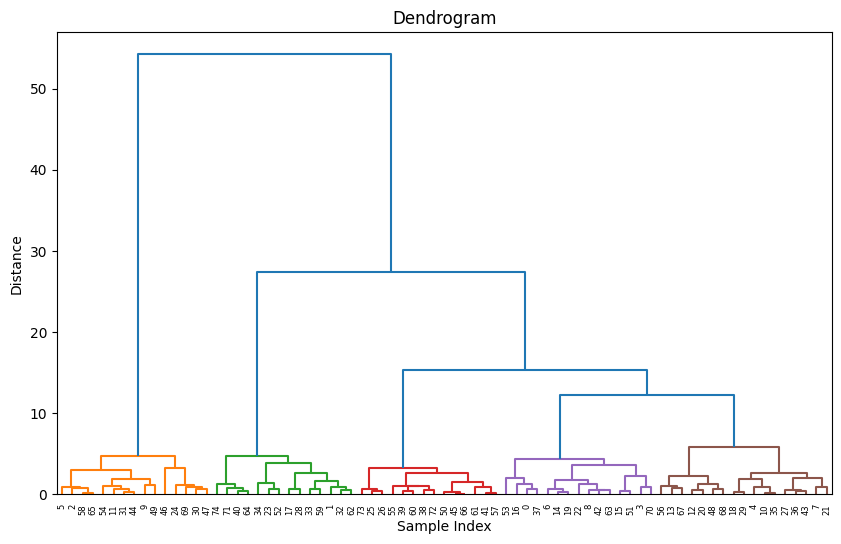

Преимущества и недостатки аглометративной кластеризации

Преимущества:

• адаптация к различным ситуациям и способность обнаружения кластеров произвольной формы;

• возможность формирования информативной иерархии кластеров, которая позволяет выбирать оптимальное число кластеров или лучше изучать структуру данных.

Недостатки:

• использование большого количества вычислительных ресурсов и памяти из-за работы со всей матрицей расстояний между объектами;

• чувствительность к выбору критерия объединения кластеров, а также неустойчивость к шуму и выбросам, что может сильно искажать иерархию кластеров.

Дополнительные источники

Статья «Modern hierarchical, agglomerative clustering algorithms», Daniel Müllner.

Документация: описание AgglomerativeClustering, AgglomerativeClustering (алгоритм).

Видео: один, два, три.

---

Спектральная кластеризация

Спектральная кластеризация — метод кластеризации на основе спектральных свойств матрицы сходства графа, который представляет собой набор точек данных, связанных друг с другом в зависимости от их сходства. Основная идея заключается в преобразовании матрицы сходства графа в лаплассиан для получения его собственных векторов, которые в дальнейшем используются для проекции данных в новое пространство более низкой размерности для лучшей разделимости, где затем применяется другой метод кластеризации, например, такой как K-средних.

Существуют различные способы построения матрицы сходства, среди которых наиболее популярными являются следующие:

• nearest_neighbors (путём вычисления графа ближайших соседей);

• rbf (с использованием радиальной базисной функции);

• предварительно вычисленные, где признаки представлены как матрица сходства или граф ближайших соседей;

• различные ядра: xi-квадрат, линейное, полиномиальное, сигмоидальное и другие.

Также существуют различные стратегии разложения лаплассиана на собственные вектора и значения:

• ARPACK (ARnoldi PACKage) — это программный пакет на языке Fortran, который реализует итерационный метод Арнольди для нахождения нескольких собственных значений и собственных векторов большой разреженной матрицы. Метод Арнольди — это обобщение метода Ланцоша, который строит ортогональный базис подпространства Крылова, порождённого матрицей и начальным вектором, а затем проецирует исходную собственную задачу на это подпространство.

• LOBPCG (Locally Optimal Block Preconditioned Conjugate Gradient) — это метод, который реализует локально оптимальный, блочный, предобусловленный, сопряжённый градиент для нахождения нескольких наименьших по модулю собственных значений и собственных векторов большой положительно определённой матрицы. Основная идея LOBPCG заключается в том, что на каждой итерации он выбирает следующее приближение к собственному вектору так, чтобы минимизировать квадратичную форму, связанную с собственной задачей на трёхмерном подпространстве, порождённом текущим приближением, предобусловленным остатком и последним обновлением. Это делается с помощью метода Релея-Ритца, который находит оптимальные линейные комбинации этих векторов.

• AMG (Algebraic Multigrid methods) — это класс алгоритмов для решения больших систем уравнений, возникающих при дискретизации дифференциальных уравнений. В контексте кластеризации AMG методы уменьшают размер матрицы, переводя её на грубую сетку, где она имеет меньше элементов, но сохраняет свои свойства. Это делается с помощью двух операций: сглаживания и коррекции. Сглаживание — это простой итерационный метод, который уменьшает ошибку в приближённом решении собственной задачи. Коррекция — это переход на грубую сетку, где решается упрощённая собственная задача, а затем возвращается на тонкую сетку для корректировки решения. Этот процесс повторяется несколько раз, пока не будет достигнута нужная точность.

Стоит отметить, что последние 2 метода являются более быстрыми, но менее стабильными.

Принцип работы спектральной кластеризации ARPACK с RBF ядром

Алгоритм строится следующим образом:

• 1) на основе матрицы сходства графа строится его нормализованный лаплассиан и диагональная матрица степеней вершин графа, где — единичная матрица;

• 2) далее с помощью алгоритма ARPACK вычисляются k-собственных векторов лаплассиана с указанием сдвига для ускорения вычислений (sigma), случайного вектора (v0), а также наибольших по модулю собственных значений (which="LM") так как они будут расположены ближе всего к сдвигу, что в конечном счёте вернёт наименьшие собственные вектора;

• 3) полученные вектора нормализуются по степеням вершин графа, чтобы быть независимыми от весов вершин, после чего в даннных векторах изменяется знак, чтобы стать детерменированными (такой подход позволяет избежать неоднозначности в знаках собственных векторов при использовании различных реализаций алгоритма);

• 4) из модифицированных собственных векторов формируется матрица вложения, к которой применяется алгоритм K-Means, который спрогнозирует в конечном счёте итоговые метки.

Импорт необходимых библиотек

import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse.linalg import eigsh
from scipy.sparse.csgraph import laplacian as csgraph_laplacian
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans, SpectralClustering
from sklearn.metrics.pairwise import rbf_kernel
from sklearn.metrics.cluster import adjusted_rand_score

Реализация на Python с нуля

class ArpackSpectralClustering:
    def __init__(self, n_clusters=8, gamma=1.0, random_state=None):
        self.n_clusters = n_clusters
        self.gamma = gamma
        self.random_state = random_state

    @staticmethod
    def _deterministic_vector_sign_flip(u):
        # Flip the sign of the vectors to make them deterministic
        max_abs_rows = np.argmax(np.abs(u), axis=1)
        signs = np.sign(u[range(u.shape[0]), max_abs_rows])

        return u * signs[:, np.newaxis]

    def _spectral_embedding(self, affinity):
        laplacian, diag_vertex_degrees = csgraph_laplacian(affinity, normed=True, return_diag=True)
        laplacian *= -1

        arpack_v0 = np.random.RandomState(self.random_state).uniform(-1, 1, laplacian.shape[0])
        _, evecs = eigsh(laplacian, k=self.n_clusters, sigma=1.0, which="LM", tol=0, v0=arpack_v0)
        norm_evecs = evecs.T[self.n_clusters::-1] / diag_vertex_degrees
        embedding = self._deterministic_vector_sign_flip(norm_evecs)

        return embedding[:self.n_clusters].T

    def fit_predict(self, X):
        affinity_matrix = rbf_kernel(X, gamma=self.gamma)
        embedding = self._spectral_embedding(affinity_matrix)
        kmeans = KMeans(n_clusters=self.n_clusters, n_init='auto', random_state=self.random_state)
        labels = kmeans.fit_predict(embedding)

        return labels

Загрузка датасета

X3, y3 = make_moons(n_samples=200, noise=0.05, random_state=0)
X3 = StandardScaler().fit_transform(X3)
print(y3)


[0 1 1 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1
 0 0 1 1 0 0 1 1 0 0 0 1 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 1 0 0 1 0 1 1
 1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0 0 1 0 0
 0 0 0 0 1 0 1 1 0 0 0 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 1 1 0 0 0 0 1 1
 0 1 1 1 0 0 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 1 1
 0 0 1 0 0 0 0 0 0 1 0 1 1 0 1]

Обучение моделей и оценка полученных результатов

Поскольку спектральное преобразование матрицы сходства графа позволяет выявлять скрытую геометрическую структуру данных, алгоритм спектральной кластеризации может применяться к нелинейно разделимым данным и показывать довольно хорошие результаты кластеризации сложных форм, что видно из результатов ниже.

SpectralClustering

sc = ArpackSpectralClustering(n_clusters=2, gamma=10, random_state=0)
sc_pred_res = sc.fit_predict(X3)
sc_ari = adjusted_rand_score(y3, sc_pred_res)
print(f'Adjusted Rand Score for SpectralClustering: {sc_ari}', '', sep='n')
print('prediction', sc_pred_res, sep='n')


Adjusted Rand Score for SpectralClustering: 1.0

prediction
[0 1 1 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1
 0 0 1 1 0 0 1 1 0 0 0 1 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 1 0 0 1 0 1 1
 1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0 0 1 0 0
 0 0 0 0 1 0 1 1 0 0 0 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 1 1 0 0 0 0 1 1
 0 1 1 1 0 0 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 1 1
 0 0 1 0 0 0 0 0 0 1 0 1 1 0 1]

SpectralClustering (scikit-learn)

sk_sc = SpectralClustering(n_clusters=2, gamma=10, random_state=0)
sk_sc_pred_res = sk_sc.fit_predict(X3)
sk_sc_ari = adjusted_rand_score(y3, sk_sc_pred_res)
print(f'Adjusted Rand Score for sk SpectralClustering: {sk_sc_ari}', '', sep='n')
print('prediction', sk_sc_pred_res, sep='n')


Adjusted Rand Score for sk SpectralClustering: 1.0

prediction
[0 1 1 0 1 1 0 1 0 1 0 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 1 1 1 0 0 0 1 1 0 1 1
 0 0 1 1 0 0 1 1 0 0 0 1 1 0 1 1 0 1 0 0 1 0 0 1 0 1 0 1 0 0 1 0 0 1 0 1 1
 1 0 1 0 0 1 1 0 1 1 1 0 0 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 0 0 0 1 0 0 1 0 0
 0 0 0 0 1 0 1 1 0 0 0 1 0 1 0 0 1 1 1 0 0 0 1 1 1 1 0 1 0 1 1 0 0 0 0 1 1
 0 1 1 1 0 0 1 0 1 1 0 0 1 1 0 1 1 1 0 1 1 1 0 0 0 0 1 1 1 0 0 0 1 0 1 1 1
 0 0 1 0 0 0 0 0 0 1 0 1 1 0 1]

Визуализация прогнозов

plt.figure(figsize=(12, 5))

plt.subplot(121)
plt.scatter(X3[:, 0], X3[:, 1], c=sc_pred_res, cmap='Spectral')
plt.title('SpectralClustering')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

plt.subplot(122)
plt.scatter(X3[:, 0], X3[:, 1], c=sk_sc_pred_res, cmap='Spectral')
plt.title('SpectralClustering (scikit-learn)')
plt.xlabel("Feature 1")

plt.show()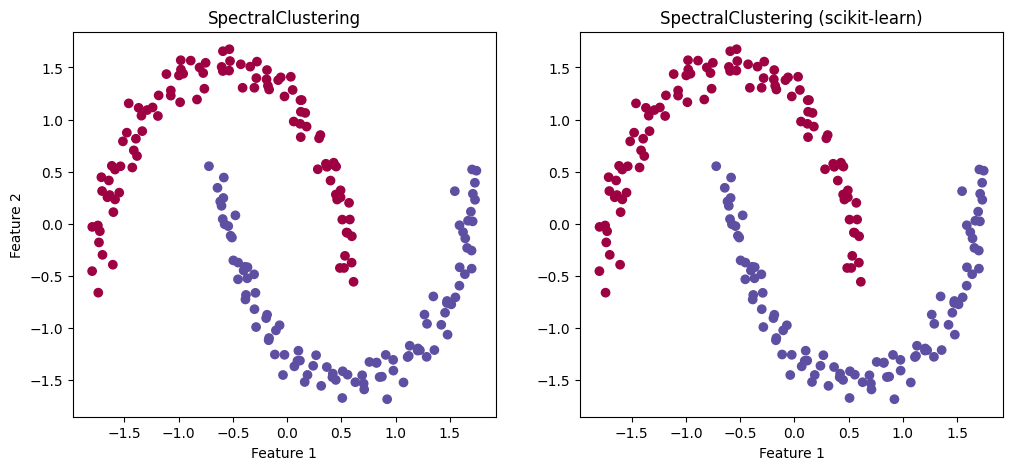

Преимущества и недостатки спектральной кластеризации

Преимущества:

• работа с кластерами сложных форм;

• возможность обработки многомерных данных из-за понижения размерности перед их кластеризацией;

• устойчивость к выбросам и шуму в данных из-за учёта их глобальной структуры, а не только локальной.

Недостатки:

• сложность конфигурации из-за большого количества гиперпараметров;

• высокая вычислительная сложность и потребление памяти при работе с большими объёмами данных, что может быть частично решено с помощью безматричных методов или случайных проекций.

Дополнительные источники

Статья «On Spectral Clustering: Analysis and an algorithm», Andrew Y. Ng, Michael I. Jordan, Yair Weiss.

Документация: описание SpectralClustering, SpectralClustering (алгоритм).

Видео: один, два, три.

---

DBSCAN

Более интересным алгоритмом кластеризации является DBSCAN (Density-Based Spatial Clustering of Applications with Noise), который основан на плотности точек в пространстве. Он группирует вместе точки, которые находятся близко друг к другу и отмечает как выбросы точки, которые лежат в областях с низкой плотностью. Помимо того что DBSCAN может обнаруживать кластеры произвольной формы и выбросы в данных, его главная особенность заключается в самостоятельном определении необходимого количества кластеров, что избавляет от необходимости в их подборе.

Для вычисления попарных расстояний и ближайших соседей точек в DBSCAN используется модифицированная реализация k-ближайших соседей, которая является алгоритмом обучения без учителя и представлена в scikit-learn в виде класса NearestNeighbors.

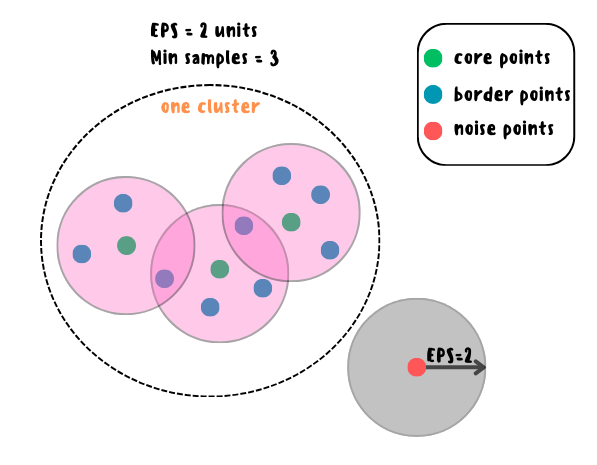
Принцип работы DBSCAN

Наиболее важными параметрами, влияющими на результат кластеризации, являются eps (максимально допустимое расстояние между точками, чтобы считаться соседями) и min_samples (минимальное количество точек в окрестности другой точки, чтобы считаться базовой точкой), а сами же точки в данных подразделяются на 3 вида:

• Core points (базовые точки) — точки в кластере, имеющие min_samples соседей в своём окружении eps или более. Это означает, что точки лежат в области высокой плотности данных.

• Border points (пограничные точки) — точки в кластере, которые имеют меньше, чем min_samples соседей в своём окружении eps, но лежат в окружении eps других базовых точек. Это означает, что точки лежат на границе кластеров.

• Noise points (шумовые точки) — это выбросы, которые не принадлежат ни к одному кластеру, то есть точки расположены в области низкой плотности данных.

Алгоритм строится следующим образом:

• 1) изначально все метки кластеров помечаются как шумовые;

• 2) после для каждой точки в своём окружении находятся соседи и на их основе отбираются базовые точки;

• 3) на основе базовых точек и соседей в своём окружении с помощью метода _dbscan_inner обновляются метки кластеров, которые и будут конечным прогнозом.

_dbscan_inner строится следующим образом:

• 1) непомеченным базовым точкам присваиваются текущие метки и они добавляются в очередь для дальнейшей обработки;

• 2) из данной очереди для каждой базовой точки находятся соседи, где каждому непомеченному соседу присваивается текущая метка и он добавляется в очередь из шага 1;

• 3) далее текущая метка увеличивается на 1 и шаг 2 повторяется пока очередь не станет пустой.

В результате данного процесса каждой точке присваивается метка соответствующего кластера, к которому она принадлежит. Точки, которые не принадлежат ни к одному кластеру, остаются шумовыми с меткой -1.

Импорт необходимых библиотек

import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.neighbors import NearestNeighbors
from sklearn.datasets import make_circles
from sklearn.metrics import adjusted_rand_score
from sklearn.preprocessing import StandardScaler

Реализация на Python с нуля

class DBSCANClustering:
    def __init__(self, eps=0.5, min_samples=5, metric='euclidean', algorithm='auto', leaf_size=30):
        self.eps = eps
        self.min_samples = min_samples
        self.metric = metric
        self.algorithm = algorithm
        self.leaf_size = leaf_size

    @staticmethod
    def _dbscan_inner(core_points, neighborhoods, labels):
        label, queue = 0, []

        for point in range(len(core_points)):
            # if the point is already assigned a label or not a core point, skip it
            if not core_points[point] or labels[point] != -1:
                continue

            labels[point] = label
            queue.append(point)

            while queue:
                current_point = queue.pop(0)
                # if the point is a core point, get it's neighbors
                if core_points[current_point]:
                    current_neighbors = neighborhoods[current_point]

                    for neighbor in current_neighbors:
                        if labels[neighbor] == -1:
                            labels[neighbor] = label
                            queue.append(neighbor)

            label += 1

    def fit_predict(self, X):
        nn = NearestNeighbors(n_neighbors=self.min_samples, radius=self.eps, metric=self.metric,
                              algorithm=self.algorithm, leaf_size=self.leaf_size)

        # find the neighbors for each point within the given radius
        neighborhoods = nn.fit(X).radius_neighbors(X, return_distance=False)
        labels = np.full(len(X), -1, dtype=np.intp)
        core_points = np.asarray([len(n) >= self.min_samples for n in neighborhoods])

        self._dbscan_inner(core_points, neighborhoods, labels)
        self.labels_ = labels

        return self.labels_

Загрузка датасета

X4, y4 = make_circles(n_samples=250, noise=0.05, factor=0.5, random_state=0)
X4 = StandardScaler().fit_transform(X4)
print(y4)


[1 0 0 1 1 1 1 0 0 1 1 1 0 1 0 0 1 1 1 0 1 0 1 0 1 0 0 0 1 0 1 0 0 1 1 1 1
 0 0 1 0 0 0 1 0 0 1 0 0 1 0 1 1 0 0 0 1 0 1 0 1 0 0 1 1 1 0 1 1 1 1 1 1 0
 1 0 1 0 1 0 0 0 0 0 0 1 1 0 0 0 1 0 0 1 0 0 1 1 0 1 1 0 1 0 0 0 1 0 1 0 0
 1 1 1 0 0 0 0 1 0 1 0 1 1 0 1 1 0 1 1 1 1 0 1 1 1 0 1 0 1 0 1 1 0 0 0 0 0
 0 0 0 1 1 0 1 1 0 0 1 1 1 0 0 0 0 1 1 1 1 1 0 1 0 0 0 0 0 1 0 0 0 1 0 0 1
 1 0 0 1 0 1 1 1 0 0 1 0 1 1 0 1 1 1 1 1 0 1 1 1 1 0 1 0 0 1 1 0 1 1 0 1 1
 0 0 0 1 0 1 1 1 0 1 1 0 1 0 1 0 0 0 0 1 0 0 1 0 1 0 0 1]

Обучение моделей и оценка полученных результатов

Как можно заметить, DBSCAN также отлично справился с кластеризацией данных сложной формы, однако выбор оптимальных eps и min_samples на практике может оказаться довольно трудной задачей, поскольку данные параметры существенно влияют на результаты кластеризации.

Частично данную проблему можно решить с использованием HDBSCAN — модификации DBSCAN, которая автоматически находит подходящее значение eps для каждого кластера, используя иерархический подход, что позволяет определять кластеры разной плотности и повысить устойчивость к выбросам.

Ещё одной интересной модификацией, похожей на HDBSCAN, является OPTICS (Ordering Points To Identify the Clustering Structure), где используется граф достижимости, который определяет достижимое расстояние для каждой точки, которая в дальнейшем будет относиться к ближайшему кластеру. Такой подход позволяет ещё лучше определять кластеры разной плотности, особенно если они расположены близко друг к другу, однако это увеличивает время работы алгоритма.

DBSCAN

dbscan = DBSCANClustering(eps=0.3, min_samples=3)
dbscan_pred_res = dbscan.fit_predict(X4)
dbscan_ari = adjusted_rand_score(y4, dbscan_pred_res)
print(f'Adjusted Rand Score for DBSCAN: {dbscan_ari}', '', sep='n')
print('prediction', dbscan_pred_res, sep='n')


Adjusted Rand Score for DBSCAN: 1.0

prediction
[0 1 1 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 0 1 0 1 0 1 1 1 0 1 0 1 1 0 0 0 0
 1 1 0 1 1 1 0 1 1 0 1 1 0 1 0 0 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 1
 0 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 1 1 1 0 1 0 1 1
 0 0 0 1 1 1 1 0 1 0 1 0 0 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 1 1 1 1 1
 1 1 1 0 0 1 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0
 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 1 0 0 1 0 0 1 0 0
 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 0 1 0 1 1 0]

DBSCAN (scikit-learn)

sk_dbscan = DBSCAN(eps=0.3, min_samples=3)
sk_dbscan_pred_res = sk_dbscan.fit_predict(X4)
sk_dbscan_ari = adjusted_rand_score(y4, sk_dbscan_pred_res)
print(f'Adjusted Rand Score for sk DBSCAN: {sk_dbscan_ari}', '', sep='n')
print('prediction', sk_dbscan_pred_res, sep='n')


Adjusted Rand Score for sk DBSCAN: 1.0

prediction
[0 1 1 0 0 0 0 1 1 0 0 0 1 0 1 1 0 0 0 1 0 1 0 1 0 1 1 1 0 1 0 1 1 0 0 0 0
 1 1 0 1 1 1 0 1 1 0 1 1 0 1 0 0 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 0 1
 0 1 0 1 0 1 1 1 1 1 1 0 0 1 1 1 0 1 1 0 1 1 0 0 1 0 0 1 0 1 1 1 0 1 0 1 1
 0 0 0 1 1 1 1 0 1 0 1 0 0 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 0 0 1 1 1 1 1
 1 1 1 0 0 1 0 0 1 1 0 0 0 1 1 1 1 0 0 0 0 0 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0
 0 1 1 0 1 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 1 1 0 0 1 0 0 1 0 0
 1 1 1 0 1 0 0 0 1 0 0 1 0 1 0 1 1 1 1 0 1 1 0 1 0 1 1 0]

Визуализация прогнозов

plt.figure(figsize=(12, 5))

plt.subplot(1, 2, 1)
plt.scatter(X4[:, 0], X4[:, 1], c=dbscan_pred_res, cmap='rainbow')
plt.title('DBSCAN')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")

plt.subplot(1, 2, 2)
plt.scatter(X4[:, 0], X4[:, 1], c=sk_dbscan_pred_res, cmap='rainbow')
plt.title('DBSCAN (scikit-learn)')
plt.xlabel("Feature 1")

plt.show()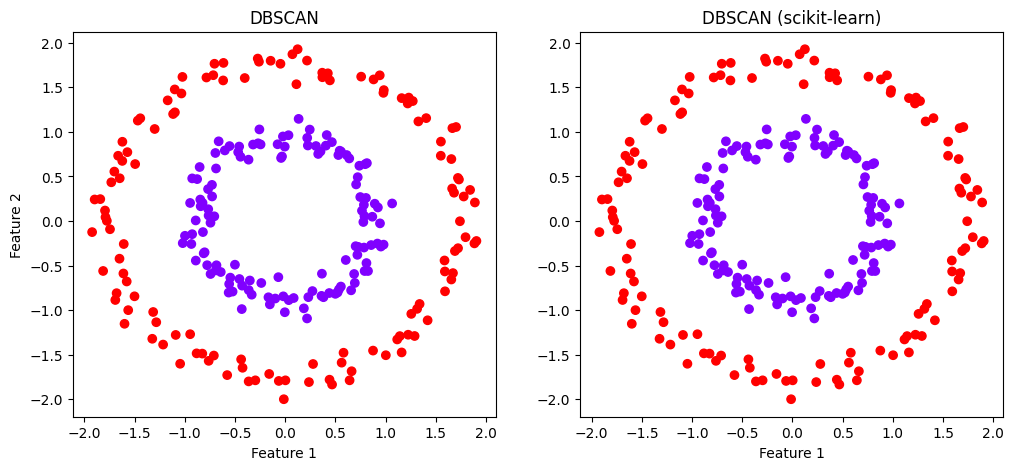

Преимущества и недостатки DBSCAN

Преимущества:

• устойчив к выбросам;

• не требуется заранее указывать количество кластеров;

• способность находить кластеры произвольной формы, а также шумовые точки в данных.

Недостатки:

• плохая работа с кластерами разной плотности;

• требуется большой объём памяти для хранения расстояний между всеми точками;

• высокая чувствительность к выбору параметров eps и min_samples, что может сильно повлиять на качество кластеризации в негативную сторону.

Дополнительные источники

Статьи:

• «DBSCAN: Optimal Rates For Density-Based Cluster Estimation», Daren Wang, Xinyang Lu and Alessandro Rinaldo;

• «HDBSCAN: Density based Clustering over Location Based Services», Md Farhadur Rahman, Weimo Liu Saad Bin Suhaim, Saravanan Thirumuruganathan, Nan Zhang, Gautam Das;

• «OPTICS: Ordering Points To Identify the Clustering Structure», Mihael Ankerst, Markus M. Breunig, Hans-Peter Kriegel, Jörg Sander.

Документация:

• описание DBSCAN ;

• описание HDBSCAN ;

• описание OPTICS ;

• DBSCAN (алгоритм);

• HDBSCAN (алгоритм);

• OPTICS (алгоритм).

Видео:

• DBSCAN: один, два, три.

• HDBSCAN: один, два.

• OPTICS: один, два.

---

Affinity Propagation

Ещё более продвинутым подходом относительно предыдущего алгоритма кластеризации является метод распространения близости (affinity propagation), который основан на концепции соотношения между данными и выборе из них экземпляров — наиболее репрезентативных образцов, которые представляются центроидами кластеров и группируют возле себя все остальные данные.

Соотношения между данными описываются с помощью матриц сходства S (similarity matrix), доступности A (availability matrix) и ответственности R (responsibility matrix), а наиболее важными параметрами при настройке алгоритма являются damping (фактор затухания, который не дает алгоритму слишком быстро менять своё мнение о том, какие точки данных лучше всего подходят друг другу) и preference (мера предпочтения точки быть экземпляром для себя или для других точек: чем больше это значение, тем больше вероятность быть экземпляром).

Принцип работы Affinity Propagation

Рассмотрим следующий пример для лучшего понимания сути данного алгоритма на интуитивном уровне. Представьте, что в школе есть много учеников, которые хотят найти своих друзей. Каждый ученик имеет свои предпочтения с кем он хочет дружить, исходя из общих интересов, характера, внешности и так далее. Например, один ученик любит футбол, другой ученик любит музыку, третий ученик любит математику. Эти предпочтения можно измерить числом, которое показывает насколько сильно ученик хочет дружить с другим учеником. Это называется сходством: чем оно больше, тем больше шансов, что ученики станут друзьями.

В данном случае Affinity propagation — это алгоритм, который помогает ученикам найти своих друзей на основе их предпочтений. Происходит это следующим образом:

• Сначала каждый ученик оценивает насколько он хочет дружить с другими учениками. Например, ученик A может сказать, что он хочет дружить с учеником B на 8 из 10, с учеником C на 6 из 10, с учеником D на 4 из 10 и так далее. Эти оценки можно рассчитать с помощью отрицательного квадратичного евклидова расстояния и записать в виде матрицы сходства, где каждая строка и столбец соответствуют ученику, а каждая ячейка содержит сходство между двумя учениками.

• Затем каждый ученик отправляет сообщения другим ученикам, в которых говорит насколько он хочет, чтобы они были его друзьями. Это называется ответственностью. Ответственность — это степень, с которой ученик выбирает другого ученика в качестве своего друга. Ответственность зависит не только от сходства, но и от того насколько другие ученики хотят быть друзьями с тем же учеником. Например, если ученик A хочет дружить с учеником B, но ученик B не хочет дружить с учеником A, то ответственность ученика A к ученику B будет низкой. Ну а если ученик A хочет дружить с учеником C и ученик C тоже хочет дружить с учеником A, то ответственность ученика A к ученику C будет высокой. Ответственность можно вычислить по формуле:

где r(i, k) — это ответственность ученика i к ученику k, s(i, k) — это сходство ученика i к ученику k, a(i, k') — это доступность ученика i к ученику k', которая будет объяснена ниже. Ответственность можно также записать в виде матрицы, где каждая строка и столбец соответствует ученику, а каждая ячейка содержит ответственность между двумя учениками.

• Далее каждый ученик получает сообщения от других учеников, в которых они говорят насколько они хотят, чтобы он был их другом. Это называется доступностью. Доступность — это степень, с которой ученик подходит для роли друга для другого ученика. Доступность зависит не только от ответственности, но и от того, насколько другие ученики подходят для роли друзей для того же ученика. Например, если ученик A хочет дружить с учеником B и ученик B хочет дружить с учеником A, то доступность ученика A к ученику B будет высокой. Ну а если ученик A хочет дружить с учеником C, но ученик C не хочет дружить с учеником A, то доступность ученика A к ученику C будет низкой. Доступность можно вычислить по формуле:

где a(i, k) — это доступность ученика i к ученику k, r(k, k) — это ответственность ученика k к себе, r(i', k) - это ответственность другого ученика i' к ученику k. Доступность можно также записать в виде матрицы, где каждая строка и столбец соответствует ученику, а каждая ячейка содержит доступность между двумя учениками.

• Алгоритм повторяет эти шаги пока не найдет оптимальное решение, в котором каждый ученик имеет своего друга. Этот друг называется экземпляром. Экземпляры — это ученики, которые лучше всего подходят для роли друзей для других учеников. Количество экземпляров зависит от того, какие предпочтения задаются для учеников. Если предпочтения не задаются, то они равны медиане сходств. Экземпляры можно определить по формуле:

где e(i) — это экземпляр ученика i, r(i, k) — это ответственность ученика i к ученику k, a(i, k) — это доступность ученика i к ученику k. Эта формула означает, что ученик i выбирает в качестве своего друга того ученика k, для которого сумма ответственности и доступности максимальна. Если ученик i выбирает себя в качестве своего друга, то он является экземпляром. Если ученик i выбирает другого ученика k в качестве своего друга, то он принадлежит к тому же кластеру, что и ученик k. Кластер — это группа учеников, которые имеют одного и того же друга-экземпляра.

Данный алгоритм строится следующим образом:

• 1) на основе отрицательного квадратичного расстояния находится матрица сходства, а также нулями инициализируются матрицы доступности и ответственности;

• 2) из матрицы сходства удаляются вырождения, а также добавляется небольшой шум;

• 3) далее итеративно обновляются значения матриц доступности и ответственности на основе временной матрицы, представленной изначально как сумма матриц сходства и доступности, чтобы найти максимальное сходство между точками данных и потенциальными экземплярами;

• 4) из этой матрицы вычисляются максимальные значения по столбцам, а также вторые по величине значения, которые используются для вычитания из матрицы сходства, чтобы получить новую матрицу ответственности;

• 5) при обновлении значений матрицы доступности, временная матрица заполняется положительными значениями матрицы ответственности, чтобы посчитать сумму сообщений между точками о том, насколько сильно они хотят быть экземплярами.

• 6) затем из данной матрицы вычитается её сумма по столбцам, чтобы получить отрицательную матрицу доступности, а также временная матрица обрезается по нулю для получения положительной матрицы доступности;

• 7) также при обновлении значений матрицы доступности и ответственности к временной матрице применяется коэффициент затухания для избегания численных колебаний при обновлении значений;

• 8) экземпляры с положительной суммой ответственности и доступности становятся центрами кластеров;

• 9) после каждой итерации проверяется условие сходимости алгоритма с использованием матрицы сходимости экземпляров: если число экземпляров не меняется в течение заданного числа итераций или если число итераций достигает максимума, то алгоритм останавливается;

• 10) в конце уточняется итоговый набор экземпляров и меток кластеров через выбор лучших экземпляров для каждого кластера из его членов на основе максимальной суммы сходств между ними;

• 11) полученные метки кластеров и будут итоговым прогнозом.

Импорт необходимых библиотек

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import AffinityPropagation
from sklearn.metrics import euclidean_distances, adjusted_rand_score

Реализация на Python с нуля

class AffinityPropagationClustering:
    def __init__(self, damping=0.5, max_iter=200, convergence_iter=15, preference=None, random_state=0):
        self.damping = damping
        self.max_iter = max_iter
        self.convergence_iter = convergence_iter
        self.preference = preference
        self.random_state = random_state

    @staticmethod
    def _affinity_propagation_inner(similarity_matrix, preference, convergence_iter, max_iter,
                                   damping, random_state):
        rng = np.random.RandomState(random_state)
        n_samples = similarity_matrix.shape[0]
        samples_indexes = np.arange(n_samples)

        # place preference on the diagonal of similarity matrix
        similarity_matrix.flat[:: (n_samples + 1)] = preference
        availability_matrix = np.zeros((n_samples, n_samples))
        responsibility_matrix = np.zeros((n_samples, n_samples))  # initialize messages
        exemplars_convergence_matrix = np.zeros((n_samples, convergence_iter))

        # remove degeneracies
        similarity_matrix += (np.finfo(similarity_matrix.dtype).eps * similarity_matrix +
                              np.finfo(similarity_matrix.dtype).tiny * 100) * 
                              rng.standard_normal(size=(n_samples, n_samples))

        for iter in range(max_iter):
            temp_matrix = availability_matrix + similarity_matrix   # compute responsibilities
            max_indexes = np.argmax(temp_matrix, axis=1)
            max_values = temp_matrix[samples_indexes, max_indexes]
            temp_matrix[samples_indexes, max_indexes] = -np.inf
            second_max_values = np.max(temp_matrix, axis=1)

            # temp_matrix = new_responsibility_matrix
            np.subtract(similarity_matrix, max_values[:, None], temp_matrix)
            max_responsibility = similarity_matrix[samples_indexes, max_indexes] - second_max_values
            temp_matrix[samples_indexes, max_indexes] = max_responsibility

            # damping
            temp_matrix *= 1 - damping
            responsibility_matrix *= damping
            responsibility_matrix += temp_matrix

            # temp_matrix = Rp; compute availabilities
            np.maximum(responsibility_matrix, 0, temp_matrix)
            temp_matrix.flat[:: n_samples + 1] = responsibility_matrix.flat[:: n_samples + 1]

            # temp_matrix = -new_availability_matrix
            temp_matrix -= np.sum(temp_matrix, axis=0)
            diag_availability_matrix = np.diag(temp_matrix).copy()
            temp_matrix.clip(0, np.inf, temp_matrix)
            temp_matrix.flat[:: n_samples + 1] = diag_availability_matrix

            # damping
            temp_matrix *= 1 - damping
            availability_matrix *= damping
            availability_matrix -= temp_matrix

            # check for convergence
            exemplar = (np.diag(availability_matrix) + np.diag(responsibility_matrix)) > 0
            exemplars_convergence_matrix[:, iter % convergence_iter] = exemplar
            n_exemplars = np.sum(exemplar, axis=0)

            if iter >= convergence_iter:
                exemplars_sum = np.sum(exemplars_convergence_matrix, axis=1)
                unconverged = np.sum((exemplars_sum == convergence_iter) +
                                     (exemplars_sum == 0)) != n_samples

                if (not unconverged and (n_exemplars > 0)) or (iter == max_iter):
                    break

        exemplar_indixes = np.flatnonzero(exemplar)
        n_exemplars = exemplar_indixes.size  # number of detected clusters

        if n_exemplars > 0:
            cluster_indices = np.argmax(similarity_matrix[:, exemplar_indixes], axis=1)
            cluster_indices[exemplar_indixes] = np.arange(n_exemplars)  # Identify clusters

            # refine the final set of exemplars and clusters and return results
            for k in range(n_exemplars):
                cluster_members = np.where(cluster_indices == k)[0]
                best_k = np.argmax(np.sum(similarity_matrix[cluster_members[:, np.newaxis],
                                                            cluster_members], axis=0))
                exemplar_indixes[k] = cluster_members[best_k]

            cluster_indices = np.argmax(similarity_matrix[:, exemplar_indixes], axis=1)
            cluster_indices[exemplar_indixes] = np.arange(n_exemplars)
            labels = exemplar_indixes[cluster_indices]

            # Reduce labels to a sorted, gapless, list
            cluster_centers_indices = np.unique(labels)
            labels = np.searchsorted(cluster_centers_indices, labels)
        else:
            cluster_centers_indices = []
            labels = np.array([-1] * n_samples)

        return cluster_centers_indices, labels

    def fit_predict(self, X):
        self.affinity_matrix_ = -euclidean_distances(X, squared=True)

        if self.preference is None:
            self.preference = np.median(self.affinity_matrix_)

        params = (self.affinity_matrix_, self.preference, self.convergence_iter, self.max_iter,
                  self.damping, self.random_state)

        self.cluster_centers_indices_, self.labels_ = self._affinity_propagation_inner(*params)
        self.cluster_centers_ = X[self.cluster_centers_indices_]

        return self.labels_

Код для отрисовки графика

def plot_connected_points(X, labels, centers, cmap):
    for i in range(len(X)):
        color = cmap(labels[i] / len(centers))
        plt.plot([X[i, 0], centers[labels[i], 0]], [X[i, 1], centers[labels[i], 1]], c=color, alpha=0.8)

Загрузка датасета

X5, y5 = make_blobs(n_samples=300, centers=9, cluster_std=0.5, random_state=0)
print(y5)


[1 1 1 6 5 7 0 3 2 5 8 4 1 2 0 1 6 2 1 6 6 0 6 2 5 5 5 8 8 4 7 3 8 8 0 7 4
 6 2 0 4 4 7 1 7 5 8 0 5 4 0 3 8 8 2 2 4 7 6 7 4 5 4 5 3 8 4 8 8 4 6 6 2 3
 7 7 4 8 4 1 4 8 7 3 7 8 6 1 3 7 5 0 8 3 5 2 4 2 2 2 7 4 6 2 2 7 5 5 7 2 7
 0 5 7 1 5 3 2 8 3 1 4 2 1 8 5 1 5 5 2 2 1 6 7 4 3 3 3 5 3 6 6 6 5 4 4 2 8
 6 5 7 0 8 8 8 1 6 1 6 6 0 7 7 6 0 8 0 3 6 4 7 3 1 6 0 0 4 1 5 6 1 2 1 0 8
 3 0 7 5 4 3 0 5 2 1 4 6 1 0 0 0 3 8 5 0 6 0 1 5 4 8 2 4 0 1 6 3 7 0 8 4 8
 1 8 1 5 0 0 7 5 4 4 3 0 7 3 2 4 3 5 0 7 6 1 0 7 1 3 5 1 7 3 6 7 6 2 1 3 8
 5 2 3 1 4 6 2 3 8 0 1 6 2 7 6 0 7 1 4 3 5 4 0 2 2 2 1 8 8 7 3 2 0 3 2 3 6
 5 8 2 3]

Обучение моделей и оценка полученных результатов

Affinity Propagation показал отличный результат без настройки параметров, определив верно не только количество кластеров, но и присвоив метки всем точкам данных. Данный алгоритм также способен показывать хорошие результаты для кластеров любой формы и плотности, однако может потребоваться настройка параметров, но это всё равно проще, чем в случае с DBSCAN или HDBSCAN.

AffinityPropagation

ap = AffinityPropagationClustering()
ap_pred_res = ap.fit_predict(X5)
ap_ari = adjusted_rand_score(y5, ap_pred_res)
print(f'Adjusted Rand Score for AffinityPropagation: {ap_ari}', '', sep='n')
print('prediction', ap_pred_res, sep='n')


Adjusted Rand Score for AffinityPropagation: 1.0

prediction
[1 1 1 7 6 0 8 5 2 6 3 4 1 2 8 1 7 2 1 7 7 8 7 2 6 6 6 3 3 4 0 5 3 3 8 0 4
 7 2 8 4 4 0 1 0 6 3 8 6 4 8 5 3 3 2 2 4 0 7 0 4 6 4 6 5 3 4 3 3 4 7 7 2 5
 0 0 4 3 4 1 4 3 0 5 0 3 7 1 5 0 6 8 3 5 6 2 4 2 2 2 0 4 7 2 2 0 6 6 0 2 0
 8 6 0 1 6 5 2 3 5 1 4 2 1 3 6 1 6 6 2 2 1 7 0 4 5 5 5 6 5 7 7 7 6 4 4 2 3
 7 6 0 8 3 3 3 1 7 1 7 7 8 0 0 7 8 3 8 5 7 4 0 5 1 7 8 8 4 1 6 7 1 2 1 8 3
 5 8 0 6 4 5 8 6 2 1 4 7 1 8 8 8 5 3 6 8 7 8 1 6 4 3 2 4 8 1 7 5 0 8 3 4 3
 1 3 1 6 8 8 0 6 4 4 5 8 0 5 2 4 5 6 8 0 7 1 8 0 1 5 6 1 0 5 7 0 7 2 1 5 3
 6 2 5 1 4 7 2 5 3 8 1 7 2 0 7 8 0 1 4 5 6 4 8 2 2 2 1 3 3 0 5 2 8 5 2 5 7
 6 3 2 5]

AffinityPropagation (scikit-learn)

sk_ap = AffinityPropagation()
sk_ap_pred_res = sk_ap.fit_predict(X5)
sk_ap_ari = adjusted_rand_score(y5, sk_ap_pred_res)
print(f'Adjusted Rand Score for sk AffinityPropagation: {sk_ap_ari}', '', sep='n')
print('prediction', sk_ap_pred_res, sep='n')


Adjusted Rand Score for sk AffinityPropagation: 1.0

prediction
[1 1 1 7 6 0 8 5 2 6 3 4 1 2 8 1 7 2 1 7 7 8 7 2 6 6 6 3 3 4 0 5 3 3 8 0 4
 7 2 8 4 4 0 1 0 6 3 8 6 4 8 5 3 3 2 2 4 0 7 0 4 6 4 6 5 3 4 3 3 4 7 7 2 5
 0 0 4 3 4 1 4 3 0 5 0 3 7 1 5 0 6 8 3 5 6 2 4 2 2 2 0 4 7 2 2 0 6 6 0 2 0
 8 6 0 1 6 5 2 3 5 1 4 2 1 3 6 1 6 6 2 2 1 7 0 4 5 5 5 6 5 7 7 7 6 4 4 2 3
 7 6 0 8 3 3 3 1 7 1 7 7 8 0 0 7 8 3 8 5 7 4 0 5 1 7 8 8 4 1 6 7 1 2 1 8 3
 5 8 0 6 4 5 8 6 2 1 4 7 1 8 8 8 5 3 6 8 7 8 1 6 4 3 2 4 8 1 7 5 0 8 3 4 3
 1 3 1 6 8 8 0 6 4 4 5 8 0 5 2 4 5 6 8 0 7 1 8 0 1 5 6 1 0 5 7 0 7 2 1 5 3
 6 2 5 1 4 7 2 5 3 8 1 7 2 0 7 8 0 1 4 5 6 4 8 2 2 2 1 3 3 0 5 2 8 5 2 5 7
 6 3 2 5]

Визуализация прогнозов

plt.figure(figsize=(12, 5))

plt.subplot(121)
plt.scatter(X5[:, 0], X5[:, 1], c=ap_pred_res, cmap='rainbow', s=10)
plt.scatter(ap.cluster_centers_[:, 0], ap.cluster_centers_[:, 1], c='black', s=50)
plt.title('AffinityPropagation')
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plot_connected_points(X5, ap_pred_res, ap.cluster_centers_, plt.cm.rainbow)

plt.subplot(122)
plt.scatter(X5[:, 0], X5[:, 1], c=sk_ap_pred_res, cmap='rainbow', s=10)
plt.scatter(sk_ap.cluster_centers_[:, 0], sk_ap.cluster_centers_[:, 1], c='black', s=50)
plt.title('AffinityPropagation (scikit-learn)')
plt.xlabel("Feature 1")
plot_connected_points(X5, sk_ap_pred_res, sk_ap.cluster_centers_, plt.cm.rainbow)

plt.show()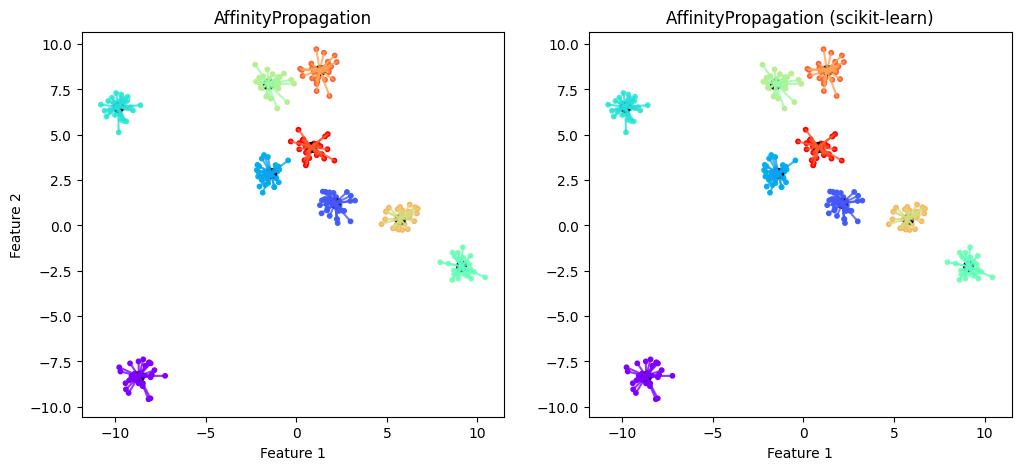

Преимущества и недостатки Affinity Propagation

Преимущества:

• высокая точность;

• автоматическое определение количества кластеров;

• не чувствителен к выбору начальных значений;

• небольшое количество гиперпараметров для настройки.

Недостатки:

• возможна чувствительность к выбросам и шуму в данных;

• высокая сложность по времени выполнения и использованию памяти, что делает затруднительным его применение к данным большого размера.

Не смотря на то, что Affinity Propagation является далеко не самым быстрым алгоритмом, на данный момент существует несколько модификаций, способных значительно повысить его скорость. Среди наиболее интересных модификаций можно выделить следующие:

• Hierarchical Affinity Propagation (HAP) — алгоритм кластеризации с использованием Affinity Propagation несколько раз на разных уровнях данных. Сначала находятся экземпляры на небольшом подмножестве данных, которые после применяются ко всему набору данных. Такой подход позволяет сократить время выполнения и уменьшить количество сообщений, передаваемых между точками, однако это может повлиять на качество кластеризации.

• Fast Affinity Propagation — модификация на основе обрезаний сообщений, которая базируется на двух основных идеях. Во-первых, сокращается размер матрицы сходства путем выбора небольшого подмножества экземпляров в качестве кандидатов в прототипы, а также вычисления сходства только между ними и всеми остальными экземплярами. Во-вторых, используется многомерный поиск для определения параметра предпочтения путем разбиения интервала возможных значений предпочтения на несколько подынтервалов и запуска алгоритма на каждом из них параллельно. Затем выбирается тот подынтервал, который даёт наилучшее качество кластеризации по некоторому установленному критерию.

• Affinity Propagation на основе пиков плотности — двухэтапный алгоритм кластеризации (DDAP), который сначала определяет пики плотности в данных с помощью алгоритма DDC (Density peaks and Distance-based Clustering), а затем использует стандартный Affinity Propagation для поиска экземпляров, которые близки к этим пикам. Такой подход позволяет значительно уменьшить количество вычислений при сопоставимом качестве кластеризации.

Дополнительные источники

Статьи:

• «Extended Affinity Propagation: Global Discovery and Local Insights», Rayyan Ahmad Khan, Rana Ali Amjad, Martin Kleinsteuber;

• «Hierarchical Affinity Propagation», Inmar E. Givoni, Clement Chung, Brendan J. Frey;

• «Fast Affinity Propagation Clustering based on Machine Learning», Shailendra Kumar Shrivastava, Dr. J.L. Rana and Dr. R.C. Jain;

• «Fast Clustering by Affinity Propagation Based on Density Peaks», Yang Li, Chonghui Guo, Leilei Sun.

Документация:

• описание Affinity Propagation, Affinity Propagation (алгоритм).

Видео: один, два.

---

The end

Вот и подошёл к концу обзор данной темы. Очень надеюсь, что вам понравилось, поскольку в дальнейшем я планирую опубликовать в подобном формате статьи по всем популярным алгоритмам машинного обучения с их реализацией с нуля на Python.

Всем успехов!

🡄 Метод главных компонент (PCA)