Мягкое знакомство с дополнительным кодом

Недавно, общаясь по видеосвязи с другом, я рассказывал ему о своих идеях по реализации нового продукта. В разговоре я упомянул добавление больших знаковых чисел в ассемблере с использованием дополнительного кода, на что получил от собеседника вопрос: «Что такое дополнительный код?» Меня немного удивила его неосведомлённость. Он уже больше 30 лет программирует на Java. Java и Python программисты (а также другие, работающие с языками *с придыханием* вроде Commodore / MicroSoft BASIC) не сталкиваются с нативным типом беззнакового целого числа. В этих языках подобные тонкости реализуются за них.

Всё это круто, но компьютер, за которым вы сидите, внутренне обрабатывает такие числа довольно простым способом, и хорошо бы знать, как именно это происходит.

Плюс это всё же наука. Так что давайте разбираться.

Что такое дополнительный код?

Дополнительный код – это система представления знаковых целых, упрощающая выполнение двоичной арифметики. Чтобы найти дополнительный код двоичного числа, вы инвертируете все его биты (изменяя 0 на 1 и наоборот), после чего прибавляете к результату единицу. Это представление упрощает построение вычислительных устройств, позволяя выполнять сложение и вычитание при помощи одной и тоже схемы, поскольку вычитание числа равнозначно прибавлению его дополнительного кода. К тому же этот приём позволяет эффективно обрабатывать изменение знаков и нулевые значения, в связи с чем он так широко используется в вычислительных системах.

Немного поупражняемся с 8-битным целым числом

Примечание: предполагаю, что вы уже знакомы с принципом работы двоичной системы исчисления. Если же нет, то вот хороший базовый материал. Кроме того, для лучшего понимания этой статьи вам потребуется знание побитовых операций. Для тех, кто недостаточно с ними знаком, тоже есть хороший ознакомительный материал.

Начнём с простого примера. Мы будем использовать 8-битные целые, потому что с ними проще работать.

5 в двоичном виде – это 00000101.

А как представить в двоичном виде -5? В дополнительном коде старший бит значения (крайний слева) используется как бит знака. Если он нулевой, то число положительное, а если равен единице – отрицательное.

Чтобы найти дополнительный код для 5 мы инвертируем все биты этого числа и затем добавляем к результату единицу.

• Инвертирование 00000101 даст нам 11111010.
• Добавление единицы к 11111010 даст 11111011.
• То есть для 00000101 дополнительным кодом является 11111011.
• В десятичном виде 11111011 – это -5.

Проделаем ещё одну операцию, чтобы вы лучше усвоили её принцип.

• 100 в двоичном виде – это 01100100.
• Инвертируя все биты 01100100, получаем 10011011.
• Добавление единицы к 10011011 даст 10011100.
• То есть дополнительным кодом для 01100100 является 10011100.
• В десятичном виде 10011100 – это -100.

Напомню, что старший бит равен нулю у положительных чисел и единице у отрицательных. Это бит знака.

Проще простого, не так ли?

Используя старший бит для обозначения знака, мы можем представить только 8-битные числа от -128 до 127. Причина в том, что устанавливая старший бит для получения числа 128, мы меняем знак этого числа на минус.

Обновление от 2023-11-23: пользователь dperrin с Hacker News высказал по этому поводу следующие мысли, которые могут показаться вам интересными:

«Когда я впервые изучал дополнительный код, то воспринял эту информацию как нужную только для сдачи теста и не стал особо разбираться, почему этот принцип работает.

Реально же он меня заинтересовал, когда я взглянул на него с позиции модульной арифметики. Если мы рассматриваем 8-битные целые числа, то они охватывают диапазон от 0 до 255, и по факту вы выполняете действия по модулю 256. Значит, числа от 0 до 127 можно рассматривать как неотрицательные числа, а числа от 128 до 255 выступают как отрицательные по модулю 256 (например, -1 mod 256 = 255)».

Реализация на схеме

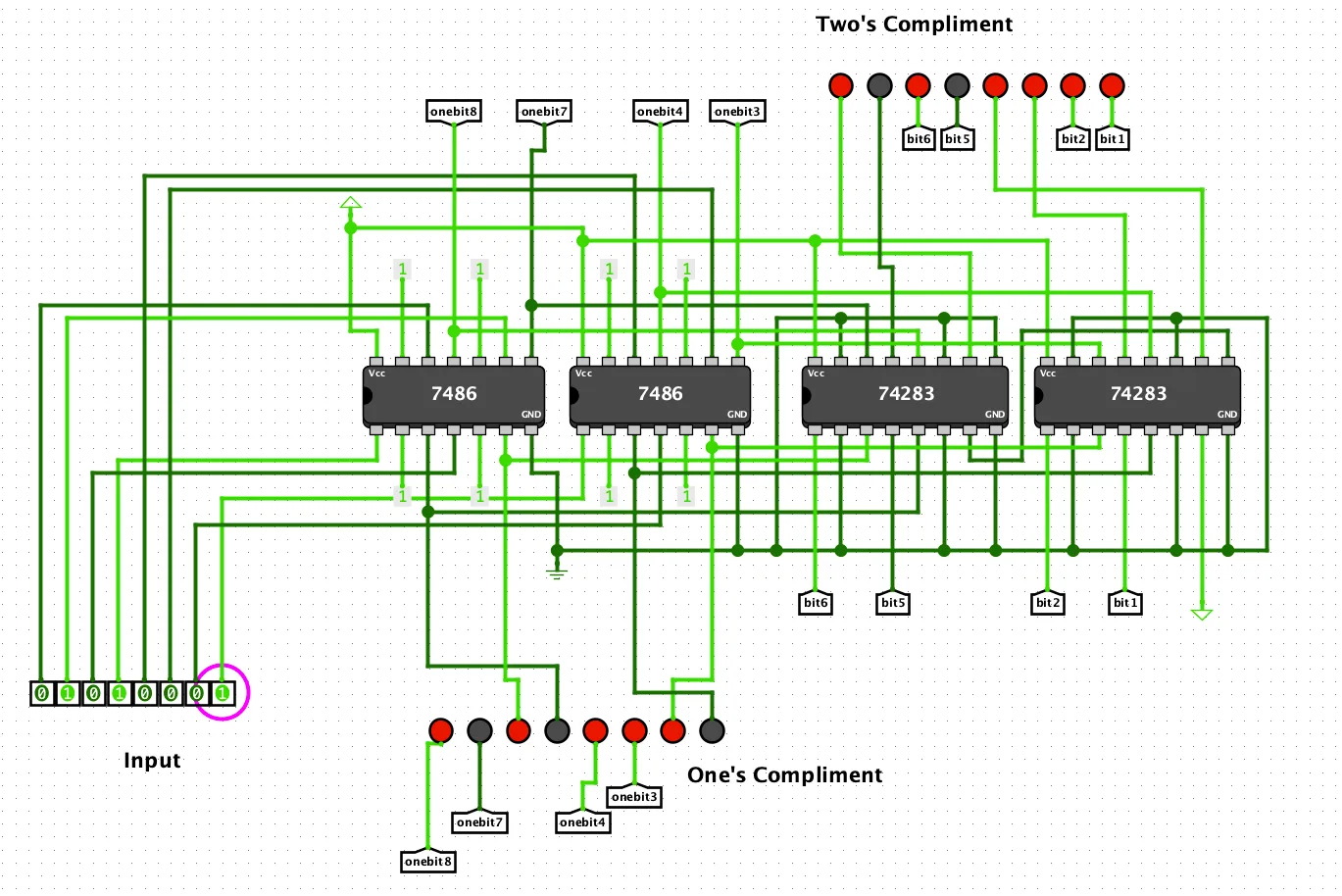
Один из стандартных способов реализации вычисления дополнительного кода – это использование схемы, получающей 8-битный ввод и выдающей его дополнительный код. Эта схема состоит из двух частей: инвертора и сумматора. Инвертор получает ввод и инвертирует все его биты, изменяя 0 на 1 и 1 на 0. Сумматор, в свою очередь, прибавляет к полученному результату единицу, что равнозначно добавлению дополнительного кода входного значения.

Для реализации этого можно использовать готовые логические вентили. Если мы хотим инвертировать бит, проще всего это будет сделать с помощью вентиля XOR. В микросхемах 74LS86 есть по 4 вентиля XOR. Можно использовать два из них для инвертирования битов.

Кстати, если вы просто будете считывать биты с вентилей 74LS86s, то получите обратный код входного значения. Подробнее об этом ниже.

В добавок к этому мы используем два 4-битных сумматора микросхемы 74LS283. Нам нужно подключить исходящий перенос первого сумматора на вход второго.

Чтобы выделить старший бит как знаковый, я использовал красный светодиод.

Вот видео схемы в действии. Здесь показано получение дополнительного кода для 5 и 100 вместе с проверкой результатов на калькуляторе:

Дополнительный квест: что за обратный код?

Обратный код – это система представления знаковых целых чисел, аналогичная дополнительному коду, но имеющая ключевое отличие. Чтобы найти обратный код двоичного числа, нужно просто инвертировать все его биты.

Обратный код стал известен тем, что использовался в вычислителе системы управления космическим кораблём Аполлон. Этот код активно применялся в первых компьютерах, потому что требует для своей реализации меньше аппаратных ресурсов, чем дополнительный код. Если взять нашу схему, то можно убрать сумматор и связанные с ним подключения, использовав для инвертирования битов вентили XOR. Такая схема будет выдавать для входного числа обратный код.

Однако у неё есть серьёзный недостаток. В этой системе существует два варианта представления нуля, +0 и -0. Это может вести к ошибкам в арифметических операциях. Например, если вы сложите +0 и -0, то получите -0. Мозг ещё не потёк?

В случае же дополнительного кода, когда нуль может быть представлен только в одной форме, такого уже не произойдёт.

Преимущество обратного кода (помимо мучений программиста) в том, что его легко реализовать в железе. Вы просто инвертируете биты.

Оперируя нашей скромной макетной платой, вы можете убрать две микросхемы справа и все провода, подключающие микросхемы XOR к сумматорам. В итоге мы будем считывать биты с микросхем XOR и получать обратный код для входного числа.

Как это использовать?

Основную часть работы за вас проделывает сам используемый язык. В некоторых языках, например, C/C++, Rust или Swift, есть знаковые и беззнаковые типы. При этом в других вроде Java, Ruby и Python такого различия нет.

Низкоуровневые языки

При использовании низкоуровневых языков, имеющих беззнаковые и знаковые типы данных, вы можете не понимать, что реализуете дополнительный код. Этот принцип неизменен, даже если вы не знаете, что конкретно происходит внутри процессора.

▍ Cи

#include <stdio.h>
#include <stdint.h>

int main() {
// 8-битное беззнаковое целое число
uint8_t unsignedEightBit = 255; // Максимальное значение для 8-битного беззнакового целого
printf("Unsigned 8-bit value: %un", unsignedEightBit);

// 8-битное знаковое целое число
int8_t signedEightBit = 127; // Максимальное значение для 8-битного знакового целого
printf("Signed 8-bit value: %dn", signedEightBit);

// Демонстрация переполнения
unsignedEightBit = 256; // Это значение вызовет переполнение
printf("Overflowed Unsigned 8-bit value: %un", unsignedEightBit);

signedEightBit = 128; // Это значение вызовет переполнение
printf("Overflowed Signed 8-bit value: %dn", signedEightBit);

return 0;
}

• Для 8-битных беззнаковых целых чисел используется тип uint8_t. Он может хранить значения от 0 до 255.
• Для знаковых 8-битных целых чисел используется тип int8_t. Он может хранить значения от -128 до 127.

Здесь будет кстати продемонстрировать условия для возникновения переполнения. Оно происходит, когда вы присваиваете типу слишком большое значение. В случае беззнаковых типов переполнение вызывает возврат к началу численного диапазона, а в случае знаковых технически поведение программы не определено, но в Си зачастую происходит аналогичный возврат.

▍ Rust

В Rust для 8-битных беззнаковых целых используется тип u8, а для 8-битных знаковых – тип i8. Этот язык предоставляет богатую систему типов и возможности безопасности, включая проверку на целочисленные переполнения в отладочных сборках. Вот пример, демонстрирующий использование обоих типов:

fn main() {
// 8-битное беззнаковое целое число
let unsigned_eight_bit: u8 = 255; // Максимальное значение для 8-битного беззнакового целого
println!("Unsigned 8-bit value: {}", unsigned_eight_bit);

// 8-битное знаковое целое число
let signed_eight_bit: i8 = 127; // Максимальное значение для 8-битного знакового целого
println!("Signed 8-bit value: {}", signed_eight_bit);

// Демонстрация переполнения
// Примечание: в случае переполнения в режиме отладки в Rust активируется механизм паники
// Для обработки переполнения можно использовать wrapping_add, saturating_add и тому подобное
let overflowed_unsigned = unsigned_eight_bit.wrapping_add(1);
println!("Overflowed Unsigned 8-bit value: {}", overflowed_unsigned);

let overflowed_signed = signed_eight_bit.wrapping_add(1);
println!("Overflowed Signed 8-bit value: {}", overflowed_signed);
}

В этом примере:

• Для 8-битных беззнаковых целых чисел используется тип u8, способный хранить значения от 0 до 255.
• Для 8-битных знаковых целых используется тип i8, способный хранить значения от -128 до 127.

В Rust переполнение обрабатывается не так, как в Си. По умолчанию проверка на переполнение реализована только в отладочных сборках языка, и в этом случае при его обнаружении срабатывает механизм паники. В релизные же сборки проверка на переполнение не включена в целях повышения быстродействия, и в этом случае Rust работает аналогично Си (производит возврат к началу диапазона). Однако в этом языке есть методы вроде wrapping_add и saturating_add, позволяющие обрабатывать переполнения явно и безопасно.

Как это реализовать на ассемблере?

Я всё ещё предпочитаю обучать людей ассемблеру начиная с ассемблера 6502. Он прост и прекрасно помогает понять основы работы компьютеров. Это также позволяет познакомиться с дополнительным кодом, поскольку внутри процессора мы ограничены работой с 8-битными значениями.

▍ Ассемблер 6502

В ассемблере 6502 понятие знаковых и беззнаковых целых чисел не определяется явно через типы данных, как это происходит в высокоуровневых языках. Вместо этого способ их различения определяется тем, как вы управляете данными в коде. Отмечу, что процессор 6502 работает с 8-битными данными и 16-битными адресами.

Ниже показан пример обработки знаковых и беззнаковых 8-битных значений на ассемблере 6502:

 LDA #$FF ; Загрузка в аккумулятор 8-битного значения (255 в десятичном виде или -1, если интерпретировать его как знаковое)
STA $0200 ; Сохранение значения в области памяти $0200

LDA #$7F ; Загрузка в аккумулятор 127 (максимальное положительное значение для 8-битного знакового целого)
STA $0201 ; Сохранение значения в области памяти $0201

• Инструкция LDA #$FF загружает в регистр-аккумулятор значение 0xFF (255 в десятичной системе). Если интерпретировать его, как беззнаковый байт, то получится 255. Если же трактовать его как знаковый байт (используя дополнительный код), то значением будет -1.
• Инструкция LDA #$7F загружает в аккумулятор значение 0x7F (127 в десятичной системе), являющегося максимумом для знакового 8-битного целого в представлении дополнительного кода.

Процессор 6502 не умеет различать знаковые и беззнаковые целые числа, поэтому программисту для правильной интерпретации передаваемых значений нужно использовать соответствующие инструкции.

Например, инструкции BPL (ветвление, если плюс) и BMI (ветвление, если минус) можно использовать для реализации ветвления на основе того, к какому знаковому числу привела последняя операция (положительному или отрицательному). При этом для сравнения беззнаковых целых чисел используются инструкции вроде BCS (ветвление, если перенос установлен) и BCC (ветвление, если переноса нет).

Это подобно вождению авто с механической коробкой передач. Автомобилю не важно, вперёд вы едете или назад – выбор нужной передачи за вами. Здесь комфортная и экономичная езда будет зависеть от своевременного включения правильной передачи. И те, кто ездит на механике, знает, что оно того стоит. Иногда.

Если у вас нет доступа к компьютеру с процессором 6502, то вы можете использовать эмулятор или онлайн-ассемблер. Мне нравится этот.

▍ Построение таблицы в Commodore BASIC

Commodore BASIC обрабатывает знаковые и беззнаковые числа внутренне. Но не может же статья на этом сайте (речь об imapenguin.com, — прим. пер.) обойтись без винтажного ПК?

Посмотрим, как это реализуется на Commodore 128 (должно работать на многих диалектах BASIC из начала 80-х):

2 PRINTCHR$(147)
3 PRINT"TWOS COMPLEMENT CHART FOR 8 BIT VALUES"
4 PRINT"----------------------------------------"
5 PRINT"POSITIVE NEGATIVE UNSIGNED BINARY"
10 FOR N=0TO127
30 T=0
40 FOR I=0 TO 7
50 B=2^I
60 IF (N AND B) = B THEN GOTO80
70 T=T+B
80 NEXT I
90 T=(T+1) AND 255
100 PRINT N,-N,T,
120 FOR I=7 TO 0 STEP -1
130 B=2^I
140 IF (T AND B) = B THEN PRINT "1";:GOTO 150
145 PRINT "0";
150 NEXT I
160 PRINT
170 NEXT

Интересно. В документации Commodore операция AND называется логическое AND. Но эту операцию можно использовать для проверки установки битов, значит, в правильных руках она будет побитовым AND.

Версия на ППВМ

Нет макетной платы – нет проблем. Вполне будет достаточно вашей карманной ППВМ.
У вас же припасена в кармане ППВМ, не так ли?

Дополнительный код на ППВМ реализуется легко. Вот пример модуля, получающего 8-битный ввод и выдающего его дополнительный код:

module TwosComplement(
input [7:0] in, // 8-битный ввод
output [7:0] out // 8-битный вывод, представляющий дополнительный код 
);

// Инвертирование всех битов входного значения; равнозначно работе наших вентилей XOR на микросхеме 74LS86
wire [7:0] inverted;
assign inverted = ~in;

// Прибавление 1 к инвертированному вводу; равнозначно работе сумматоров на нашей 74LS283 
assign out = inverted + 1;

endmodule

Поскольку ширина регистров 8 бит, эти операции будут циклически обнуляться и работать для всех 8-битных целых чисел. Как и ассемблер, ППВМ не интересует, используете вы знаковое или беззнаковое число. Вы сами должны подобрать для него правильную реализацию.

Также, если возникнет потребность поработать с обратным кодом, можете просто использовать этот инвертированный сигнал.

HP-16C

Программируемый калькулятор HP-16C поддерживает как обратный код, так и дополнительный. Это странная и диковинная штуковина, но мне нравится.

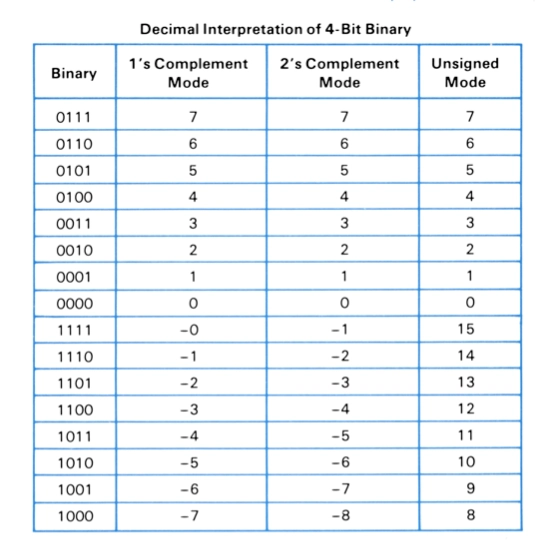
В руководстве к HP-16C есть прекрасная таблица, перечисляющая обратный и дополнительный код для всех 4-битных целых. Мне она очень пригодилась, когда я изучал эту тему около года назад.

Получилось мягко?

Дополнительный код – это система для представления знаковых чисел, упрощающая двоичную арифметику. Для нахождения дополнительного кода двоичного числа мы инвертируем все его биты (изменяя 0 на 1 и 1 на 0), а затем прибавляем к результату 1. Это представление упрощает проектирование компьютеров, позволяя выполнять сложение и вычитание на одной схеме, поскольку вычитание числа равнозначно прибавлению его дополнительного кода. Кроме того, эта техника позволяет эффективно обрабатывать изменения знаков и нулевые значения, в связи с чем используется в компьютерах по сей день.