Уже лет 50, со времён выхода первого издания «Языка программирования Си» Кернигана и Ритчи, известно, что «числа с плавающей запятой» одинарной точности имеют размер 32 бита, а числа двойной точности — 64 бита. Существуют ещё и 80-битные числа расширенной точности типа «long double». Эти типы данных покрывали почти все нужды обработки вещественных чисел. Но в последние несколько лет, с наступлением эпохи больших нейросетевых моделей, у разработчиков появилась потребность в типах данных, которые не «больше», а «меньше» существующих, потребность в том, чтобы как можно сильнее «сжать» типы данных, представляющие числа с плавающей запятой.

Я, честно говоря, был удивлён, когда узнал о существовании 4-битного формата для представления чисел с плавающей запятой. Да как такое вообще возможно? Лучший способ узнать об этом — самостоятельно поработать с такими числами. Сейчас мы исследуем самые популярные форматы чисел с плавающей запятой, создадим с использованием некоторых из них простую нейронную сеть и понаблюдаем за тем, как она работает.
«Стандартные» 32-битные числа с плавающей запятой
Прежде чем переходить к описанию «экстремальных» типов данных — давайте вспомним о стандартном типе. Стандарт IEEE 754, регламентирующий арифметику с плавающей запятой, был принят в 1985 году Институтом инженеров электротехники и электроники (Institute of Electrical and Electronics Engineers, IEEE). Типичное 32-битное число с плавающей запятой, в соответствии с этим стандартном, выглядит так:

Первый бит задаёт знак числа, следующие 8 битов представляют порядок, а остальные биты — мантиссу. Десятичное значение числа находят по следующей формуле:
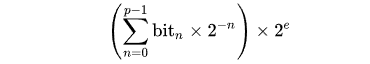
Вот — простая вспомогательная функция, которая позволит нам выводить на экран числа с плавающей запятой в их двоичном виде:
import struct
def print_float32(val: float):
""" Print Float32 in a binary form """
m = struct.unpack('I', struct.pack('f', val))[0]
return format(m, 'b').zfill(32)
print_float32(0.15625)
# > 00111110001000000000000000000000Напишем ещё одну вспомогательную функцию, которая позволяет выполнять обратное преобразование. Позже она нам пригодится:
def ieee_754_conversion(sign, exponent_raw, mantissa, exp_len=8, mant_len=23):
""" Convert binary data into the floating point value """
sign_mult = -1 if sign == 1 else 1
exponent = exponent_raw - (2 ** (exp_len - 1) - 1)
mant_mult = 1
for b in range(mant_len - 1, -1, -1):
if mantissa & (2 ** b):
mant_mult += 1 / (2 ** (mant_len - b))
return sign_mult * (2 ** exponent) * mant_mult
ieee_754_conversion(0b0, 0b01111100, 0b01000000000000000000000)
#> 0.15625И я надеюсь, что все программисты и IT‑энтузиасты знают, что точность чисел с плавающей запятой ограничена:
val = 3.14
print(f"{val:.20f}")
# > 3.14000000000000012434Это, в данном случае, не такая уж и проблема. Но, чем меньше у нас бит, тем меньше точность, на которую можно рассчитывать. И, как мы скоро увидим, точность вполне может быть проблемой. А теперь — начнём путешествие по кроличьей норе…
16-битные числа с плавающей запятой
Очевидно, раньше особой потребности в 16-битных числах с плавающей запятой не было, поэтому описание соответствующего типа было добавлено в стандарт IEEE 754 только в 2008 году. У таких чисел имеется знаковый бит, 5-битный порядок и 10-битная мантисса:

Логика преобразования десятичных представлений таких чисел в двоичные точно такая же, как и при работе с 32-битными числами, но их точность, безусловно, ниже, чем у 32-битных чисел. Выведем 16-битное число с плавающей запятой в двоичном виде:
import numpy as np
def print_float16(val: float):
""" Print Float16 in a binary form """
m = struct.unpack('H', struct.pack('e', np.float16(val)))[0]
return format(m, 'b').zfill(16)
print_float16(3.14)
# > 0100001001001000Прибегнув к методу, которым мы уже пользовались, можем выполнить обратное преобразование:
ieee_754_conversion(0, 0b10000, 0b1001001000, exp_len=5, mant_len=10)
# > 3.140625А вот как можно найти максимальное значение, представимое в виде числа типа float16:
ieee_754_conversion(0, 0b11110, 0b1111111111, exp_len=5, mant_len=10)
#> 65504.0Я использовал тут 0b11110 из-за того, что в стандарте IEEE 754 число 0b11111 зарезервировано для «бесконечности». Можно найти и возможное минимальное значение:
ieee_754_conversion(0, 0b00001, 0b0000000000, exp_len=5, mant_len=10)
#> 0.00006104Для большинства разработчиков типы, вроде описанного — это «неизведанная территория». И, судя по всему, даже в наши дни в C++ нет стандартного 16-битного типа данных для чисел с плавающей запятой. Но разнообразие типов этим не ограничивается.
16-битные числа с плавающей запятой «bfloat» (BFP16)
Этот формат чисел с плавающей запятой разработан командой Google Brain. Он спроектирован специально для нужд машинного обучения (буква «B» в его названии — это сокращение от «brain»). Это — модификация «стандартного» 16-битного формата: порядок увеличен до 8 бит, в результате диапазон значений bfloat16, на самом деле, получается таким же, как у float32. Но размер мантиссы был уменьшен до 7 бит:

Проведём небольшой эксперимент, аналогичный предыдущим:
ieee_754_conversion(0, 0b10000000, 0b1001001, exp_len=8, mant_len=7)
#> 3.140625Как уже было сказано — из‑за увеличенного порядка формат bfloat16 вмещает в себя гораздо больший диапазон значений, чем float16:
ieee_754_conversion(0, 0b11111110, 0b1111111, exp_len=8, mant_len=7)
#> 3.3895313892515355e+38Это — гораздо лучше в сравнении с 65504.0 из предыдущего примера, но, как уже было сказано, точность чисел bfloat16 ниже из‑за того, что на мантиссу приходится меньшее число бит. Можно протестировать оба типа в TensorFlow:
import tensorflow as tf
print(f"{tf.constant(1.2, dtype=tf.float16).numpy().item():.12f}")
# > 1.200195312500
print(f"{tf.constant(1.2, dtype=tf.bfloat16).numpy().item():.12f}")
# > 1.2031250000008-битные числа с плавающей запятой (FP8)
Этот (сравнительно новый) формат был предложен в 2022 году и, как может догадаться читатель, он тоже создан для целей машинного обучения. Модели становятся всё больше и больше, их всё сложнее и сложнее умещать в памяти GPU. Формат FP8 существует в двух вариантах: E4M3 (4-битный порядок и 3-битная мантисса) и E5M2 (5-битный порядок и 2-битная мантисса):

Выясним максимально возможные значения чисел для обоих вариантов FP8:
ieee_754_conversion(0, 0b1111, 0b110, exp_len=4, mant_len=3)
# > 448.0
ieee_754_conversion(0, 0b11110, 0b11, exp_len=5, mant_len=2)
# > 57344.0Формат FP8 можно использовать и в TensorFlow:
import tensorflow as tf
from tensorflow.python.framework import dtypes
a_fp8 = tf.constant(3.14, dtype=dtypes.float8_e4m3fn)
print(a_fp8)
# > 3.25
a_fp8 = tf.constant(3.14, dtype=dtypes.float8_e5m2)
print(a_fp8)
# > 3.0Нарисуем график синуса, используя оба типа:
import numpy as np
import tensorflow as tf
from tensorflow.python.framework import dtypes
import matplotlib.pyplot as plt
length = np.pi * 4
resolution = 200
xvals = np.arange(0, length, length / resolution)
wave = np.sin(xvals)
wave_fp8_1 = tf.cast(wave, dtypes.float8_e4m3fn)
wave_fp8_2 = tf.cast(wave, dtypes.float8_e5m2)
plt.rcParams["figure.figsize"] = (14, 5)
plt.plot(xvals, wave_fp8_1.numpy())
plt.plot(xvals, wave_fp8_2.numpy())
plt.show()Результат, что удивительно, не так уж и плох:
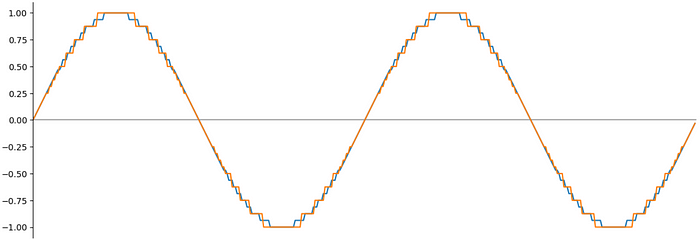
Тут ясно видны некоторые потери точности, но то, что получилось, очень даже похоже на синусоиду!
4-битные числа с плавающей запятой (FP4, NF4)
А теперь перейдём к самой «безумной» теме — к 4-битным числам с плавающей запятой (FP4). На самом деле такие числа — это самые компактные значения с плавающей запятой, соответствующие стандарту IEEE, имеющие 1 бит на знак, 2 бита на порядок и 1 бит на мантиссу:

Количество значений, которые можно сохранить в формате FP4, невелико. Все эти значения, на самом деле, помещаются в массив на 16 элементов!
Ещё одна возможная реализация 4-битных чисел с плавающей запятой представлена типом данных, называемым NormalFloat (NF4). Значения NF4 оптимизированы для сохранения нормально распределённых данных. Все возможные значения NF4 легко вывести на экран в виде небольшого списка (при исследовании других типов данных это может оказаться совсем непростой задачей):
[-1.0, -0.6961928009986877, -0.5250730514526367, -0.39491748809814453,
-0.28444138169288635, -0.18477343022823334, -0.09105003625154495, 0.0,
0.07958029955625534, 0.16093020141124725, 0.24611230194568634, 0.33791524171829224,
0.44070982933044434, 0.5626170039176941, 0.7229568362236023, 1.0]И тип FP4, и тип NF4 реализованы в Python‑библиотеке bitsandbytes. Давайте, в качестве примера, преобразуем массив [1.0, 2.0, 3.0, 4.0] в формат FP4:
from bitsandbytes import functional as bf
def print_uint(val: int, n_digits=8) -> str:
""" Convert 42 => �' """
return format(val, 'b').zfill(n_digits)
device = torch.device("cuda")
x = torch.tensor([1.0, 2.0, 3.0, 4.0], device=device)
x_4bit, qstate = bf.quantize_fp4(x, blocksize=64)
print(x_4bit)
# > tensor([[117], [35]], dtype=torch.uint8)
print_uint(x_4bit[0].item())
# > 01110101
print_uint(x_4bit[1].item())
# > 00100011
print(qstate)
# > (tensor([4.]),
# > 'fp4',
# > tensor([ 0.0000, 0.0052, 0.6667, 1.0000, 0.3333, 0.5000, 0.1667, 0.2500,
# > 0.0000, -0.0052, -0.6667, -1.0000, -0.3333, -0.5000, -0.1667, -0.2500])])Результат выглядит интересно. На выходе получилось два объекта: 16-битный массив [117, 35], содержащий наши 4 числа, и объект «состояния», в котором находятся коэффициент масштабирования 4.0 и тензор со всеми шестнадцатью FP4-числами.
Например, первое 4-битное число — это «0111» (=7). В объекте состояния можно видеть, что соответствующее ему значение с плавающей запятой — это 0.25; 0.25*4 = 1.0. Второе число — это «0101» (=5), а результирующее значение — 0.5*4 = 2.0. Третье число — это «0010», которое равняется 2, а соответствующее ему значение — 0.666*4 = 2.666, которое достаточно близко к 3, но не равно этому числу. Понятно, что при применении 4-битных значений мы столкнёмся с некоторой потерей точности. Последнее значение, «0011» — это 3, ему соответствует 1.000*4 = 4.0.
Понятно, что нет большой необходимости выполнять подобные вычисления вручную. С помощью bitsandbytes можно выполнить и обратное преобразование:
x = bf.dequantize_fp4(x_4bit, qstate)
print(x)
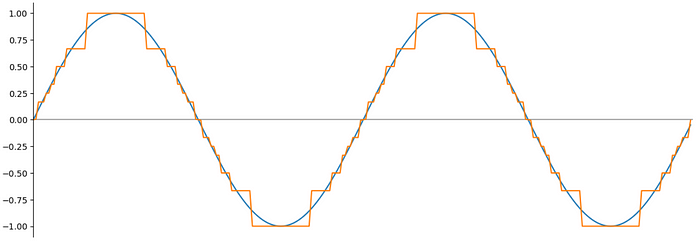
# > tensor([1.000, 2.000, 2.666, 4.000])4-битный формат чисел тоже обладает ограниченным диапазоном значений. Например, массив [1.0, 2.0, 3.0, 64.0] будет преобразован в [0.333, 0.333, 0.333, 64.0]. Но для более или менее нормализованных данных он даёт совсем неплохие результаты. Давайте, для примера, нарисуем синусоиду, воспользовавшись данными в формате FP4:
import matplotlib.pyplot as plt
import numpy as np
from bitsandbytes import functional as bf
length = np.pi * 4
resolution = 256
xvals = np.arange(0, length, length / resolution)
wave = np.sin(xvals)
x_4bit, qstate = bf.quantize_fp4(torch.tensor(wave, dtype=torch.float32, device=device), blocksize=64)
dq = bf.dequantize_fp4(x_4bit, qstate)
plt.rcParams["figure.figsize"] = (14, 5)
plt.title('FP8 Sine Wave')
plt.plot(xvals, wave)
plt.plot(xvals, dq.cpu().numpy())
plt.show()Тут, что неудивительно, видны некоторые потери точности, но то, что получилось, выглядит довольно прилично.
Если же говорить о типе NF4 — читатели сами могут попробовать исследовать его с помощью методов quantize_nf4 и dequantize_nf4; весь код останется таким же, как прежде. Но, к сожалению, на момент написания этой статьи 4-битные типы данных работают лишь с CUDA; вычисления на CPU пока не поддерживаются.
Тестирование
Теперь, в роли финального этапа этой статьи, предлагаю создать нейросетевую модель и протестировать её. При использовании Python‑библиотеки transformers можно загрузить заранее обученную модель в 4-битном формате. Для этого достаточно установить в True параметр load_in_4-bit. Но будем честны: это не приблизит нас к пониманию того, как новые форматы чисел влияют на нейросетевые модели. Вместо этого прибегнем к «игрушечному» примеру — создадим маленькую нейросеть, обучим её и воспользуемся ей, применив 4-битные числа.
Для начала создадим нейросетевую модель:
import torch
import torch.nn as nn
import torch.optim as optim
from typing import Any
class NetNormal(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.model = nn.Sequential(
nn.Linear(784, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10)
)
def forward(self, x):
x = self.flatten(x)
x = self.model(x)
return F.log_softmax(x, dim=1)Теперь надо подготовить загрузчик набора данных. Я буду использовать набор данных MNIST, содержащий 70000 изображений рукописных цифр размером 28x28 (авторские права на этот набор данных принадлежат Яну Лекуну и Коринне Кортез, он доступен по лицензии Creative Commons Attribution-Share Alike 3.0). Набор данных разделён на две части — 60000 учебных и 10000 тестовых изображений. Выбор загружаемых данных может быть выполнен в загрузчике путём использования параметра train=True|False.
from torchvision import datasets, transforms
train_loader = torch.utils.data.DataLoader(
datasets.MNIST("data", train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST("data", train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)Теперь мы готовы к тому, чтобы обучить и сохранить модель. Процесс обучения выполняется «нормальным» способом, с применением стандартного формата чисел.
device = torch.device("cuda")
batch_size = 64
epochs = 4
log_interval = 500
def train(model: nn.Module, train_loader: torch.utils.data.DataLoader,
optimizer: Any, epoch: int):
""" Train the model """
model.train()
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
loss = F.nll_loss(output, target)
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print(f'Train Epoch: {epoch} [{batch_idx * len(data)}/{len(train_loader.dataset)}]tLoss: {loss.item():.5f}')
def test(model: nn.Module, test_loader: torch.utils.data.DataLoader):
""" Test the model """
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
t_start = time.monotonic()
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item()
pred = output.argmax(dim=1, keepdim=True)
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
t_diff = time.monotonic() - t_start
print(f"Test set: Average loss: {test_loss:.4f}, Accuracy: {correct}/{len(test_loader.dataset)} ({100. * correct / len(test_loader.dataset)}%)n")
def get_size_kb(model: nn.Module):
""" Get model size in kilobytes """
size_model = 0
for param in model.parameters():
if param.data.is_floating_point():
size_model += param.numel() * torch.finfo(param.data.dtype).bits
else:
size_model += param.numel() * torch.iinfo(param.data.dtype).bits
print(f"Model size: {size_model / (8*1024)} KB")
# Обучение
model = NetNormal().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)
for epoch in range(1, epochs + 1):
train(model, train_loader, optimizer, epoch)
test(model, test_loader)
get_size(model)
# Сохранение
torch.save(model.state_dict(), "mnist_model.pt")Я, кроме того, написал вспомогательный метод get_size_kb, позволяющий узнать размер модели в килобайтах.
Вот как выглядит процесс обучения модели:
Train Epoch: 1 [0/60000] Loss: 2.31558
Train Epoch: 1 [32000/60000] Loss: 0.53704
Test set: Average loss: 0.2684, Accuracy: 9225/10000 (92.25%)
Train Epoch: 2 [0/60000] Loss: 0.19791
Train Epoch: 2 [32000/60000] Loss: 0.17268
Test set: Average loss: 0.1998, Accuracy: 9401/10000 (94.01%)
Train Epoch: 3 [0/60000] Loss: 0.30570
Train Epoch: 3 [32000/60000] Loss: 0.33042
Test set: Average loss: 0.1614, Accuracy: 9530/10000 (95.3%)
Train Epoch: 4 [0/60000] Loss: 0.20046
Train Epoch: 4 [32000/60000] Loss: 0.19178
Test set: Average loss: 0.1376, Accuracy: 9601/10000 (96.01%)
Model size: 427.2890625 KBНаша простая модель достигла точности в 96%, размер нейронной сети — 427 Кб.
А теперь — самое интересное! Создадим и протестируем 8-битную версию модели. Описание модели будет, на самом деле, таким же, как прежде. Я лишь заменил слой Linear на слой Linear8bitLt.
from bitsandbytes.nn import Linear8bitLt
class Net8Bit(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.model = nn.Sequential(
Linear8bitLt(784, 128, has_fp16_weights=False),
nn.ReLU(),
Linear8bitLt(128, 64, has_fp16_weights=False),
nn.ReLU(),
Linear8bitLt(64, 10, has_fp16_weights=False)
)
def forward(self, x):
x = self.flatten(x)
x = self.model(x)
return F.log_softmax(x, dim=1)
device = torch.device("cuda")
# Загрузка
model = Net8Bit()
model.load_state_dict(torch.load("mnist_model.pt"))
get_size_kb(model)
print(model.model[0].weight)
# Преобразование
model = model.to(device)
get_size_kb(model)
print(model.model[0].weight)
# Запуск
test(model, test_loader)Вот — выходные данные:
Model size: 427.2890625 KB
Parameter(Int8Params([[ 0.0071, 0.0059, 0.0146, ..., 0.0111, -0.0041, 0.0025],
...,
[-0.0131, -0.0093, -0.0016, ..., -0.0156, 0.0042, 0.0296]]))
Model size: 107.4140625 KB
Parameter(Int8Params([[ 9, 7, 19, ..., 14, -5, 3],
...,
[-21, -15, -3, ..., -25, 7, 47]], device='cuda:0',
dtype=torch.int8))
Test set: Average loss: 0.1347, Accuracy: 9600/10000 (96.0%)Исходная модель была загружена с использованием стандартного формата чисел с плавающей запятой. Её размер остался таким же, веса выглядят как [0.0071, 0.0059,…]. Вся «магия» заключается в преобразовании модели в cuda — она становится в 4 раза меньше. Как видно, значения весов находятся в одном и том же диапазоне, поэтому преобразование модели сложностей не вызывает. В процессе проверки модели на тестовых данных оказалось, что она не потеряла ни единого процента точности!
А теперь — 4-битная версия:
from bitsandbytes.nn import LinearFP4, LinearNF4
class Net4Bit(nn.Module):
def __init__(self):
super().__init__()
self.flatten = nn.Flatten()
self.model = nn.Sequential(
LinearFP4(784, 128),
nn.ReLU(),
LinearFP4(128, 64),
nn.ReLU(),
LinearFP4(64, 10)
)
def forward(self, x):
x = self.flatten(x)
x = self.model(x)
return F.log_softmax(x, dim=1)
# Загрузка
model = Net4Bit()
model.load_state_dict(torch.load("mnist_model.pt"))
get_model_size(model)
print(model.model[2].weight)
# Преобразование
model = model.to(device)
get_model_size(model)
print(model.model[2].weight)
# Запуск
test(model, test_loader)Вот — результаты работы:
Model size: 427.2890625 KB
Parameter(Params4bit([[ 0.0916, -0.0453, 0.0891, ..., 0.0430, -0.1094, -0.0751],
...,
[-0.0079, -0.1021, -0.0094, ..., -0.0124, 0.0889, 0.0048]]))
Model size: 54.1015625 KB
Parameter(Params4bit([[ 95], [ 81], [109],
...,
[ 34], [ 46], [ 33]], device='cuda:0', dtype=torch.uint8))
Test set: Average loss: 0.1414, Accuracy: 9579/10000 (95.79%)Мы получили интересные результаты. После преобразования размер модели уменьшился в 8 раз — с 427 до 54 Кб, но точность упала лишь на 1%. Как это возможно? Ответить на этот вопрос несложно. По крайней мере — для этой модели:
-
Как видно, веса распределены более или менее равномерно, и потеря точности не слишком велика.
-
При обработке выходных данных в модели используется Softmax, результат определяется по индексу максимального значения. Несложно понять, что при поиске максимального индекса само значение роли не играет. Например — между 0,8 и 0,9 нет никакой разницы в том случае, если другие значения — это 0,1 или 0,2.
Полагаю — важно более тщательно изучить то, что у нас получилось. Загрузим числа из тестового набора данных и ознакомимся с тем, что выдаст модель.
dataset = datasets.MNIST('data', train=False, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
]))
np.set_printoptions(precision=3, suppress=True) # Не использовать научную запись
data_in = dataset[4][0]
for x in range(28):
for y in range(28):
print(f"{data_in[0][x][y]: .1f}", end=" ")
print()Вот — выведенное на экран число, которое нужно распознать:

Посмотрим, что выдаст «стандартная» модель:
# Подавить научную запись
np.set_printoptions(precision=2, suppress=True)
# Прогноз
with torch.no_grad():
output = model(data_in.to(device))
print(output[0].cpu().numpy())
ind = output.argmax(dim=1, keepdim=True)[0].cpu().item()
print("Result:", ind)
# > [ -8.27 -13.89 -6.89 -11.13 -0.03 -8.09 -7.46 -7.6 -6.43 -3.77]
# > Result: 4Максимальный элемент находится в 5-й позиции (элементы в массивах numpy нумеруются с 0), что соответствует числу 4.
Вот — результаты работы 8-битной модели:
# > [ -9.09 -12.66 -8.42 -12.2 -0.01 -9.25 -8.29 -7.26 -8.36 -4.45]
# > Result: 4Вот что выдала 4-битная модель:
# > [ -8.56 -12.12 -7.52 -12.1 -0.01 -8.94 -7.84 -7.41 -7.31 -4.45]
# > Result: 4Хорошо видно, что реальные выходные значения у разных моделей различаются, но индекс максимального элемента остаётся одним и тем же.
Итоги
В этой статье мы исследовали разные способы представления 16-битных, 8-битных и 4-битных чисел с плавающей запятой. Мы создали нейронную сеть и смогли запустить её с применением 8-битных и 4-битных чисел. И, на самом деле, за тем, как она работает, было интересно наблюдать. Уменьшая точность используемых чисел — со стандартной до 4-битной, нам удалось снизить объём памяти, необходимый модели, в 8 раз, при этом потеря точности оказалась минимальной. Конечно, мы экспериментировали на «игрушечном» примере, в по‑настоящему больших моделях используются более сложные механизмы (тем, кто интересуется данной темой, рекомендую этот материал).
Надеюсь, эта статья помогла вам получить представление об общих идеях, лежащих в основе вычислений с плавающей запятой. Как известно, «нужда — мать изобретений». Уменьшение объёма памяти, занимаемой моделью, в 4–8 раз — это замечательное достижение, особенно учитывая разницу в цене между видеокартами с памятью в 8, 16, 32 и 64 Гб ;).
Кстати, даже 4 бита — это уже не предел. В публикации о GTPQ была упомянута возможность квантификации весов в 2 или даже в три (1,5 бита!) состояния. И последнее — по порядку, но не по важности: интересно поразмышлять о «точности» нейротрансмиттеров человеческого . Интуитивно понятно, что она не так уж и высока. Возможно, 2- или 4-битные нейросетевые модели ближе, чем другие, к тем «моделям», которые находятся в наших головах.
О, а приходите к нам работать? 

Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.
Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.
Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.
Автор:
mr-pickles






