Недавно мой старший сын решил собрать однобитный компьютер на дискретных транзисторах. Идея создания однобитного устройства может показаться дурацкой, но в данном случае речь идёт не о машине, имеющей всего две инструкции или ячейки памяти, а о размере «слова» арифметически-логического устройства (АЛУ). Малая ширина в битах позволяет получить более простую схему, но для пошаговой обработки требует использования операндов шире аппаратного лимита. Однобитные АЛУ можно назвать экстремальным решением, но они вполне имеют коммерческое применение, включая микроконтроллер MC14500B, выпущенный компанией Motorola в конце 70х.
Но эта статья немного о другом. В традициях неизменных законов соперничества между братьями и сёстрами вскоре ко мне подошёл младший сын и попросил помочь ему собрать ещё более устаревшее устройство. После некоторого обсуждения мы выбрали в качестве такого устройства калькулятор на основе реле. Затем я получил дальнейшие инструкции: печатная плата должна быть старого образца в жёлтом цвете, и все реле должны быть прозрачными.
Я изначально понимал, что мы не будем собирать схему исключительно на реле. Такая задача затянула бы реализацию проекта на месяцы. К тому же при цене прозрачных реле в $6 за единицу его общая стоимость оказалась бы слишком высока. И всё же я выяснил, что можно заставить реле выполнять реальные математические действия.
▍ Немного про АЛУ
Одной из основных составляющих любого электронного вычислительного устройства является суммирующая схема. Но, несмотря на её название, этой схемы также достаточно для реализации вычитания, умножения и деления целых чисел. Современные АЛУ обычно содержат и другие арифметические схемы, но сумматор в них всё равно является основным.
Сложение двоичных цифр по своему принципу аналогично работе с десятичными числами, только в максимально упрощённой форме. У вас есть два входа с двумя возможными значениями каждый. Также есть одно выходное значение с тем же свойством. Ещё есть бит переноса, который может либо передаваться в следующий столбец, либо использоваться в качестве сигнала о переполнении. Это поведение можно обобщить в виде следующей логической таблицы:
| In_A | In_B | Out | Out_C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Теоретически это арифметическая операция, но при внимательном рассмотрении правых столбцов становится ясно, что её можно реализовать с помощью булевой логики:
Out = In_A XOR In_B
Out_C = In_A AND In_BВ электронной схеме, если у вас есть способ построить простые логические вентили, то очевидной альтернативой будет:
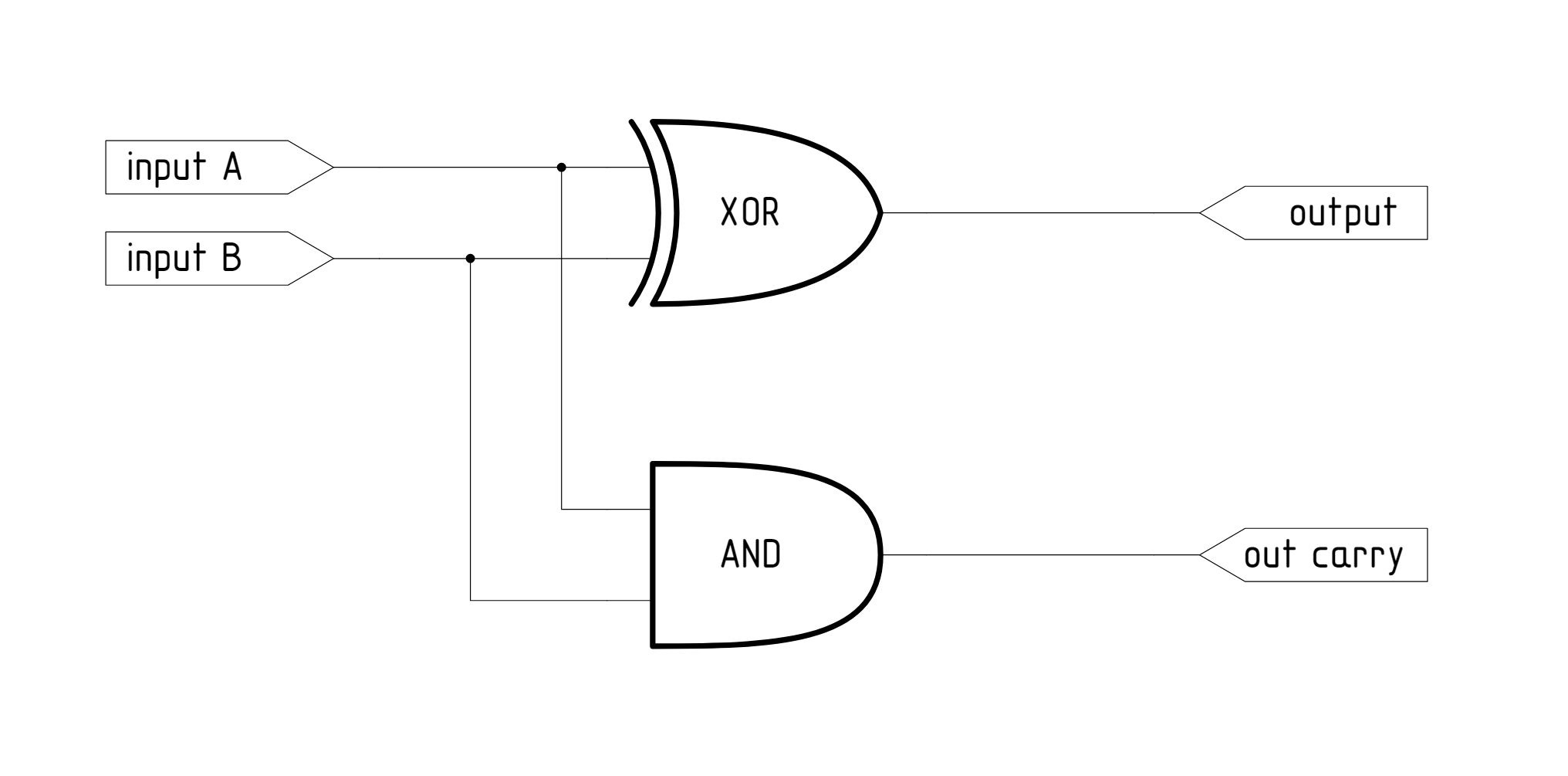
Рудиментарный однобитный сумматор
Тем не менее эта схема (полусумматор) неполноценна в том смысле, что не может учитывать перенос из предыдущего столбца. Иными словами, она не может автоматически складывать многозначные целые числа.
Чтобы собрать полноценный сумматор, нам потребуется более сложный подход с третьей входной строкой:
| In_A | In_B | In_C | Out | Out_C |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Первая половина (In_C = 0) останется такой же, что и в полусумматоре, а вот вторая будет отличаться. При наличии входного переноса выход инвертируется, и этот перенос распространяется на все кейсы, кроме In_A = In_B = 0. Равнозначный эквивалент в виде булевой алгебры получится менее элегантен, но всё равно достаточно прост для анализа:
Out = (In_A XOR In_B) XOR In_C
Out_C = (In_A AND In_B) OR (In_C AND (In_A OR In_B))В электронике это можно реализовать, в точности следуя приведённой формуле. В качестве альтернативы схему можно представить в виде двух связанных полусумматоров и операции OR, применяемой к получаемому на их выходе переносу:
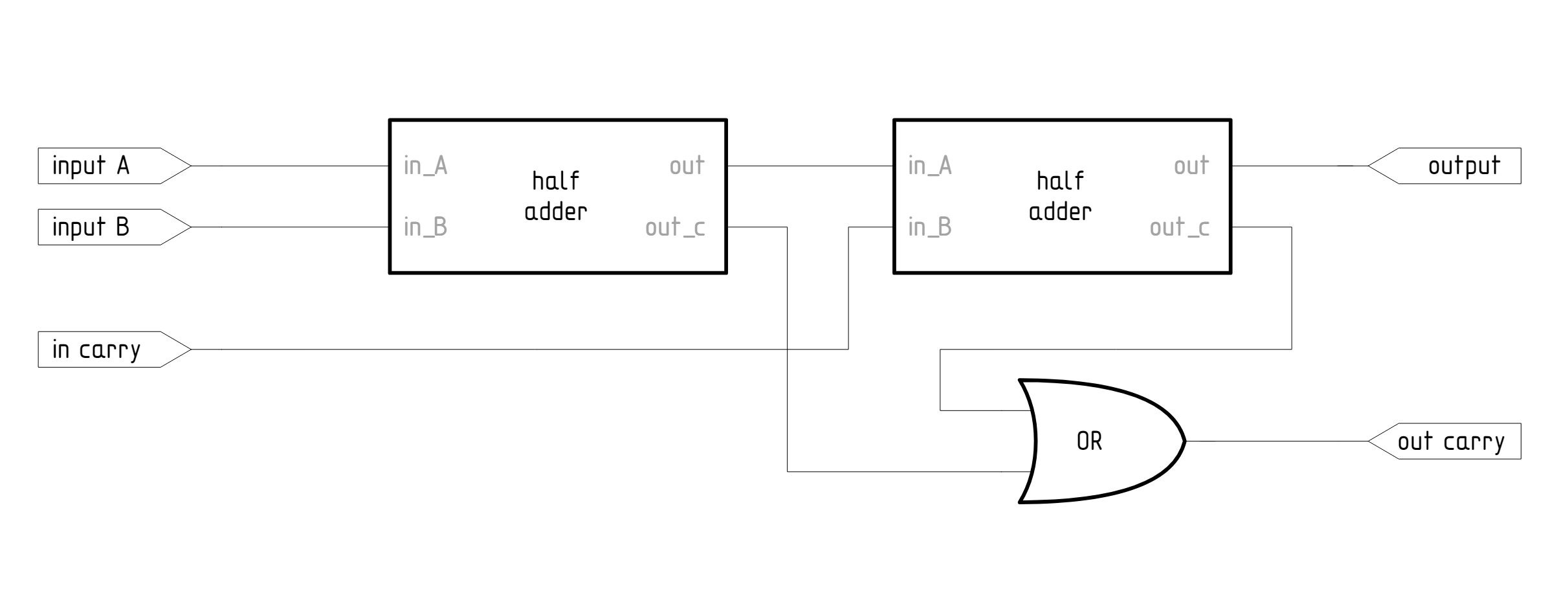
Один из вариантов представления полноценного сумматора
Полноценные сумматоры можно составить в столбец для одновременного сложения любого количества двоичных значений. Один сумматор также можно использовать последовательно в составе однобитного АЛУ – как в дизайне моего старшего сына.
▍ Логика на основе реле
Реле обладают двумя свойствами, которые делают их подходящими для построения цифровой логики: они двоичны по своему принципу действия и могут «усиливать» входные сигналы, позволяя бесконечно соединять их в цепочку.
По правде говоря, у реле есть и ряд недостатков: они медленные, дорогие, шумные, и их контакты быстро изнашиваются.
Существует много вариантов реализации логики на основе реле, отчасти ввиду разнообразия на рынке и различных способов кодирования нулей и единиц. Например, компьютер Z3 Конрада Цузе был построен на основе четырёхполюсных двухточечных устройств (4PDT) и «хитрил», также передавая вторичный, инвертированный сигнал переноса – но эта конструкция давала полноценный сумматор на основе всего двух реле.
Тем не менее использование для моего проекта минимально возможного количества реле не выглядело особо привлекательной целью. Напротив, я хотел задействовать удобные детали и реализовать чистую схему. Передо мной также стояло вышеупомянутое требование использовать реле в прозрачных корпусах.
После некоторого изучения вопроса я остановился на серии компактных реле G6C компании Omron. Эти устройства доступны как с одним переключателем SPST-NO, так и с дополнительной парой терминалов SPST-NO и SPST-NC. Вот схема SPST-NO, которую я использовал для вентиля OR:
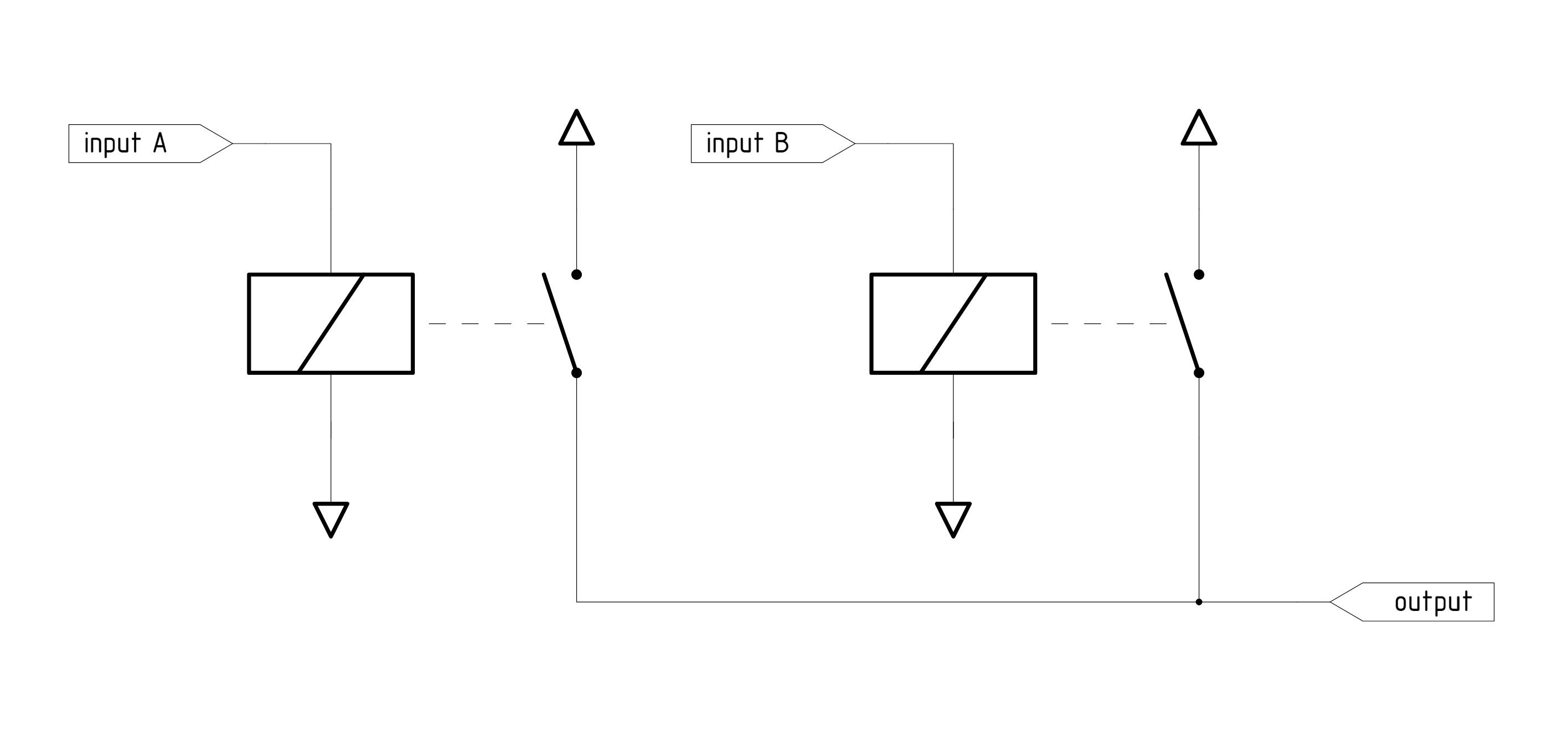
Простая схема OR на основе реле
Принцип работы этой схемы должен быть очевиден: если одно из реле активно, выход оказывается подключён к плюсовой линии подачи. В противном случае выход остаётся подвешен.
Вентиль OR также можно реализовать на основе одного реле SPDT, хотя проводящая архитектура для одного из входов подразумевает необходимость следить за «разветвлением» (нисходящей нагрузкой выхода).
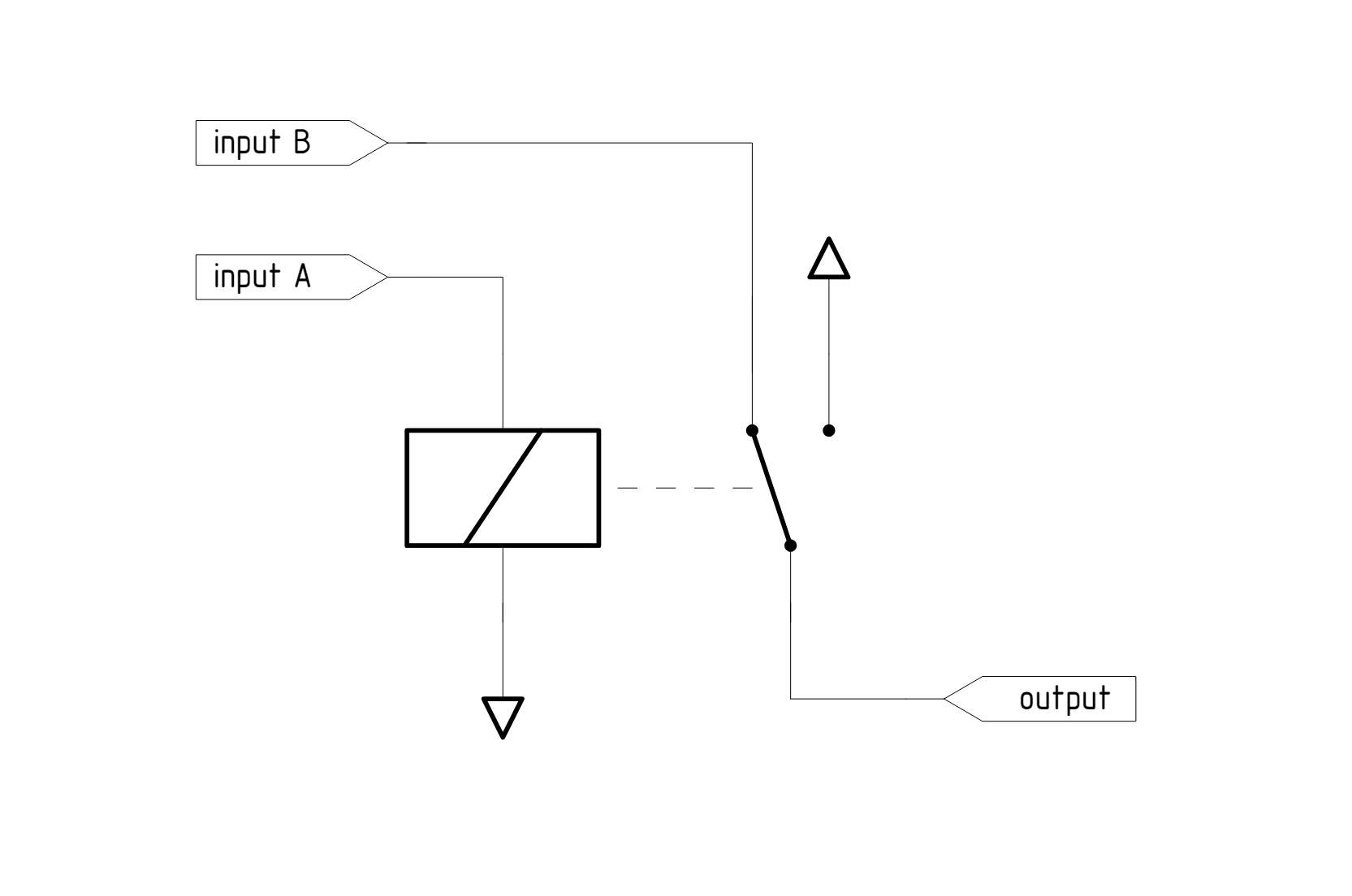
«Бюджетная» версия того же самого
Вентиль AND можно построить аналогичным образом, с помощью одного или двух реле SPST-NO:
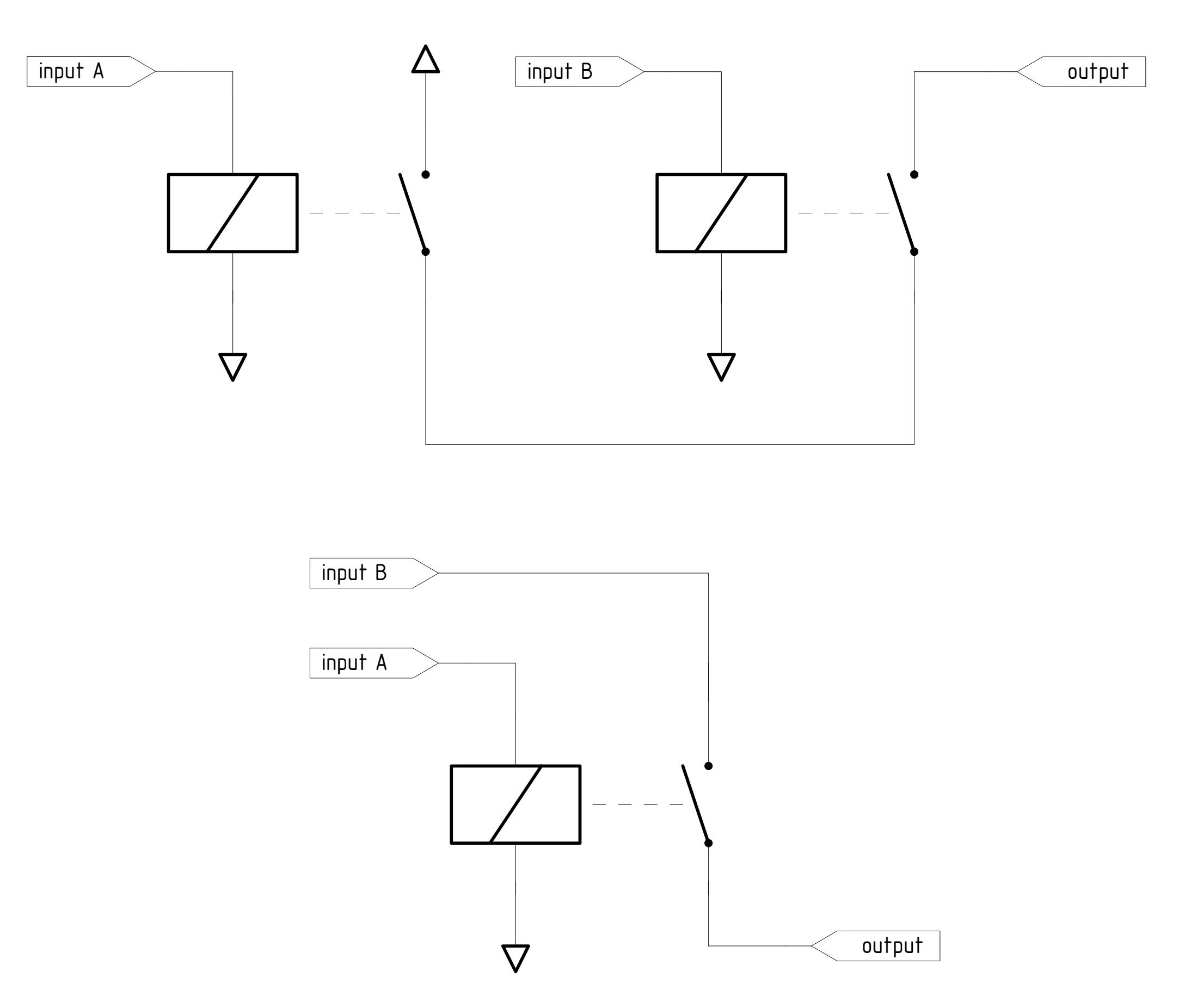
Два варианта схемы вентиль AND
Вентиль XOR собирается уже чуть сложнее и требует, как правило, двух двухходовых реле. Вот решение, которое я реализовал с помощью расширенной топологии SPST-NO + SPST-NC:
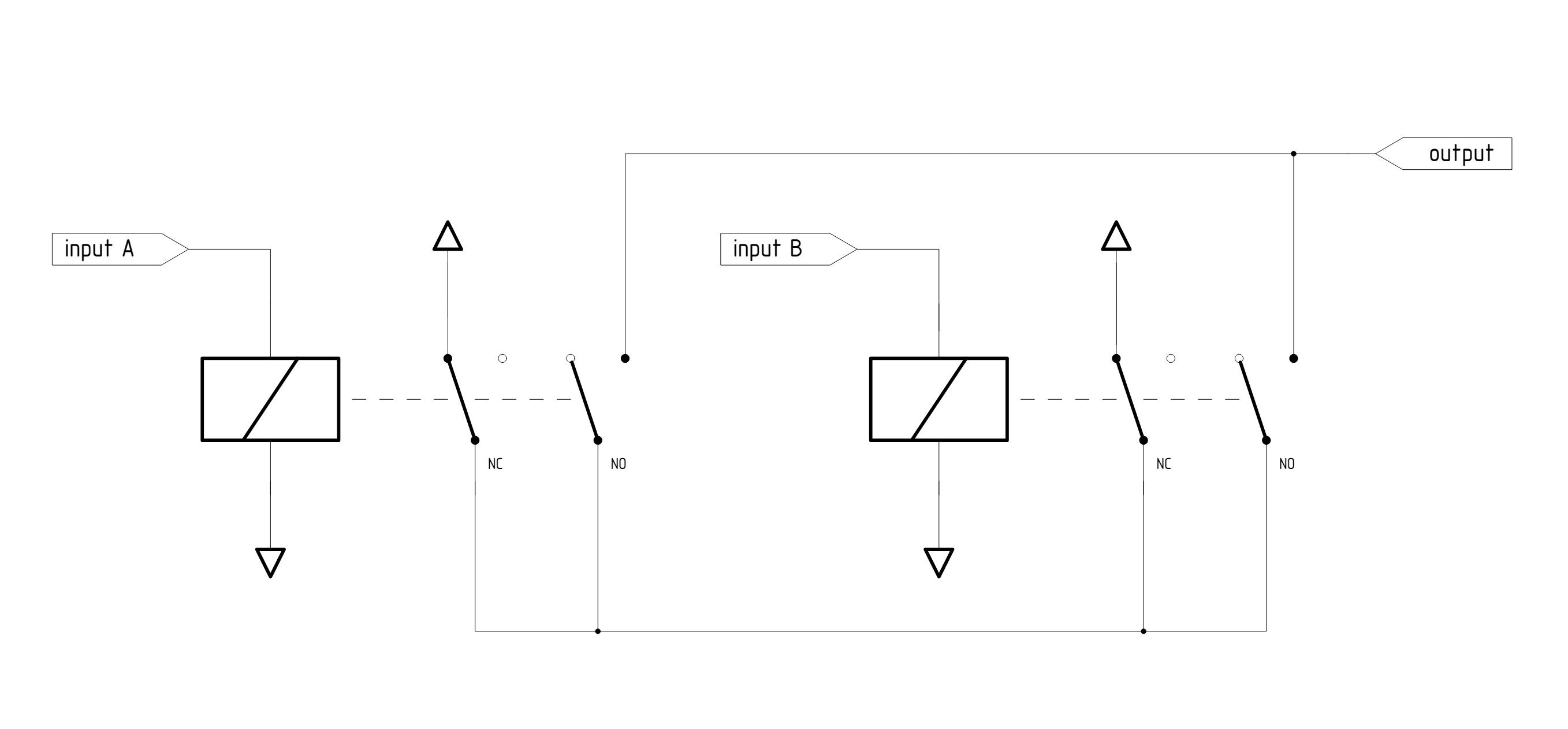
XOR на основе реле
Терминалы SPST-NO выполняют операцию OR, подключая выход к общей линии (внизу), когда любое из реле активно. Сторона SPST-NC выполняет NAND, отключая эту линию от положительного источника, когда включены оба реле.
Более компактную версию, по сути, той же архитектуры можно получить, используя реле SPDT:
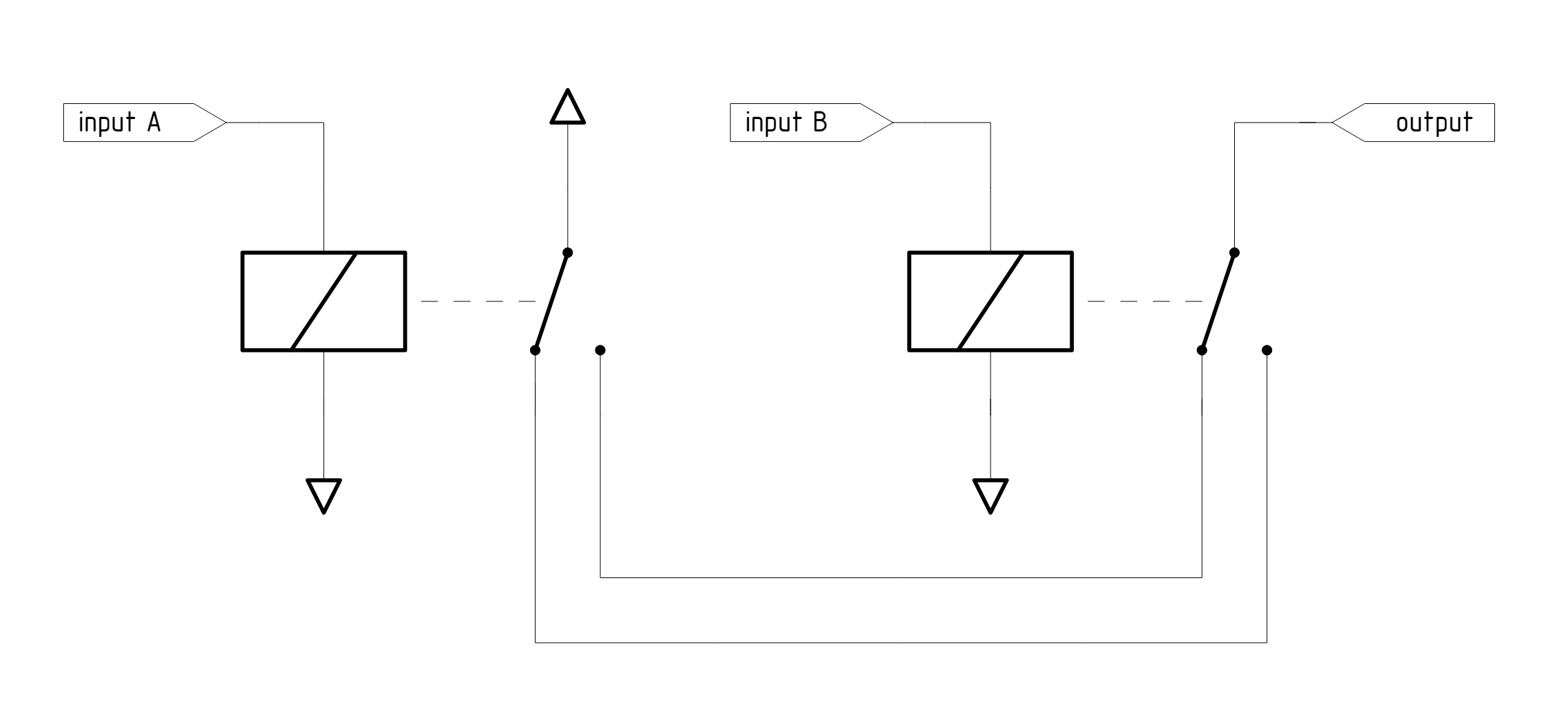
Ещё один, по сути, идентичный вариант реализации XOR
В конце я использовал два реле для самой простой реализации шести логических операций, необходимых для получения полноценного сумматора:
Out = (In_A XOR In_B) XOR In_C
Out_C = (In_A AND In_B) OR (In_C AND (In_A OR In_B))А вот крупный план раздела сумматора на печатной плате. Обратите внимание на изогнутость дорожек в «ретро» стиле и намеренное отсутствие паяльной маски:
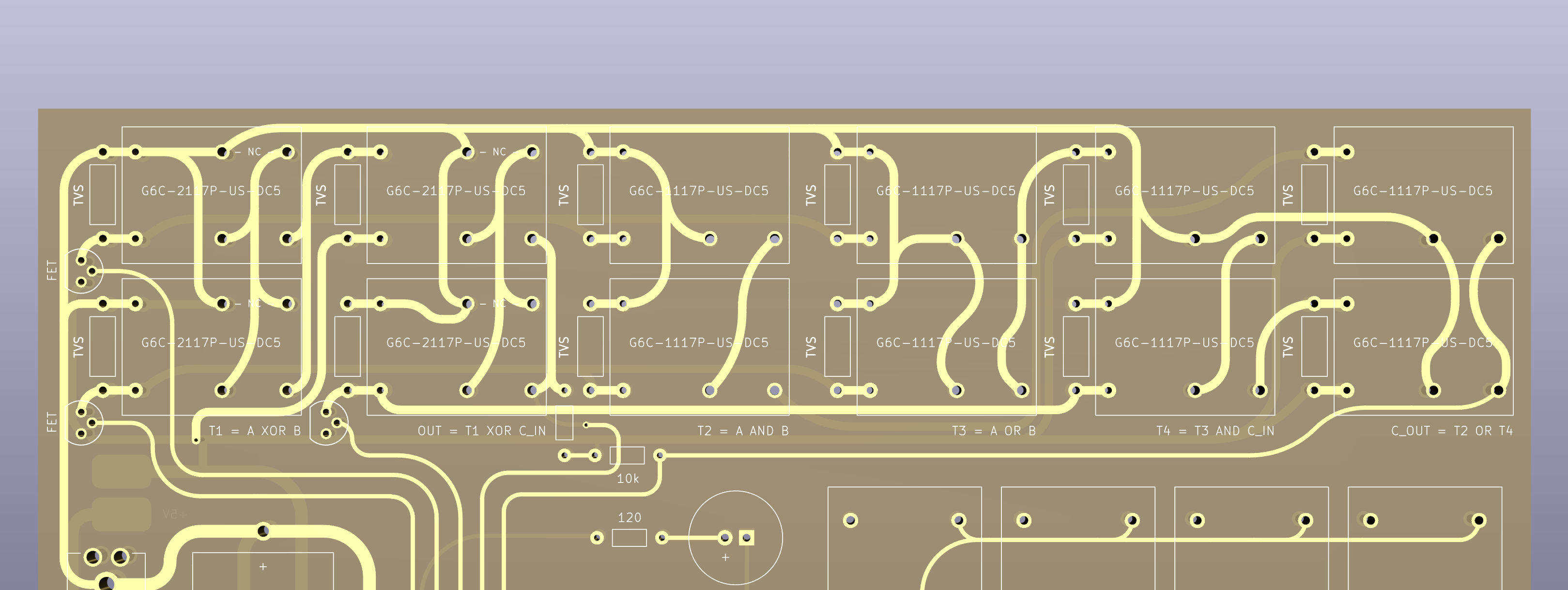
Сумматор на печатной плате
Реализация этого макета в KiCad вызвала массу негодования. Кроме того, не обошлось без продолжительной переписки с производителем печатной платы.
▍ Но ведь используются не только о реле?
Нет, по крайней мере, не сейчас. Вся «основная» плата показана ниже, вместе с самодельными стикерами для клавиш, старым переключателем, редким аксиальным электролитическим конденсатором и… да – 8-битным микроконтроллером:

Основная плата для Calc-U-Later
Микроконтроллер будет отвечать за различные вспомогательные задачи, которые потребовали бы сотен дополнительных реле. К ним относится сканирование блока клавиш, декодирование цифр, выстраивание последовательности операций, обработка ошибок и память. Тем не менее сумматор имеет чётко обозначенную роль и будет выполнять реальные математические вычисления.
Вот последовательность операций микроконтроллера при выполнении сложения:
- Установка указателя бита операнда на 0 (LSB, младший бит).
- Инициализация строки «входящего переноса» на нуль.
- Передача битов операндов на входные линии сумматора.
- Ожидание установки реле в течение ~ 20 мс.
- Обратное считывание и сохранение выходного бита сумматора.
- Передача «исходящего переноса» во «входящий перенос».
- Смещение указателя бита операнда вправо.
- Возвращение к шагу 3, пока не кончатся биты для сложения.
Иными словами, здесь всё честно, хотя микроконтроллер, в принципе, мог бы и сам выполнить работу АЛУ.
Естественно, тут речь идёт не только о сложении. На той же схеме можно выполнять и другую арифметику. Например, умножение можно разбить на серию поэтапных сложений сдвигаемых битов, в некотором роде подобно умножению столбиком:
110 × 1011 = ?
↓ ↓
110 × 1 → 110
110 × 1 → 110
110 × 0 → 000
110 × 1 → 110
-------
sum = 1000010При большом желании это смещение битов можно выполнять с помощью сумматора. Каждый сдвиг влево равнозначен сложению операнда с самим собой (то есть умножению на 2).
Вычитание тоже происходит легко. Его можно реализовать с помощью дополнения до двух (которое, в свою очередь, можно вычислить, заставив сумматор работать в качестве вентиля NOT). А разобравшись с вычитанием, несложно реализовать и деление.
▍А дисплей?
Вот здесь я не поленился и собрал специально ради этого хитроумный девайс. Его печатная плата содержит несколько 7-сегментных дисплеев полностью под управлением реле:

Крупный план пустой платы дисплея
Для сохранения контроля над числом линий данных состояние дисплея сохраняется в 8-битных регистрах-защелках (шесть микросхем 74HC259 внизу), поэтому реле присутствуют в избытке – но задача была в том, чтобы вводить цифры было так же приятно, как наблюдать АЛУ в действии.

Собранный модуль дисплея
Вот первый ролик тестирования модуля дисплея:
В следующем завораживающем аудиовизуальном ролике показано, как калькулятор обрабатывает умножение 111 на 222:
Естественно, для подобного проекта нам требовался подходящий корпус. Его мы собрали в мастерской за пару часов:

Настольный калькулятор представительского уровня из орехового дерева
Спереди калькулятор выглядит не столь впечатляюще. Вот фото сбоку:

Клавишно-дисплейный интерфейс
Ну и, наконец, вот видео, на котором калькулятор обрабатывает дроби, отрицательные числа и деление:
▍ Сколько реле реально потребуется?
Всё зависит от контекста. Если мы ограничимся примитивным входом и выходом – скажем, столбцами переключателей с фиксированным положением и индикаторами – тогда сложение и вычитание можно будет выполнять в один шаг с помощью сумматора достаточной ширины. Общее число реле будет наименьшим кратным числу входных битов.
Если же мы решим реализовать умножение и деление, то картина усложнится. В наиболее практичной форме эти операции реализуются в виде серии шагов. Вам потребуется тактовый генератор, «микросеквенсор» и массив мультиплексоров, который будет гибко подключать регистры для выполнения загрузки, сохранения и операций АЛУ.
Ещё больше всё усложнится, если мы захотим реализовать поддержку современного типа ввода, когда цифры вводятся слева направо. Поскольку для отображения и вычисления операнды должны быть выровнены по правому краю, а количество вводимых цифр заранее будет неизвестно, то потребуется дополнительная схема для выполнения необходимых сдвигов.
Сложно оценить точно, но, отталкиваясь от первых транзисторных калькуляторов вроде Friden EC-130, я бы предположил, что для подобной задачи потребуется около 500 реле.
При цене в $6 за штуку, использованные мной в проекте прозрачные детали, стали бы не самым удачным выбором. Тем не менее, взяв миниатюрные сигнальные реле, такие как Kemet EA2-5NU, мы бы уже заплатили за них меньше $1,000, а также получили более адекватный размер устройства.
Что касается питания, то оно не должно являться серьёзной проблемой – здесь речь идёт о десятках ватт – но вот производительность выступает ограничивающим фактором. В случае миниатюрных реле верхним пределом станет, пожалуй, 200 Гц. Если же брать более крупные детали, то 50 Гц уже будет много.
Теперь, когда я завершил этот «разминочный» проект, у меня может возникнуть соблазн собрать калькулятор уже исключительно на реле…
Скачать исходный код для Calc-U-Later можно здесь.
Автор: Дмитрий Брайт