В этой статье я опишу одно из последних своих дерзновений в сфере оптимизации производительности с помощью Rust. Надеюсь, что в ней вы откроете для себя какие-то новые приёмы для написания быстрого кода на Rust.
Контекст следующий: представьте, что у вас есть данные онлайн-экзамена, в котором множество пользователей отвечали на вопросы. В сыром виде эти данные выглядят так:
[
{
"user": "5ea2c2e3-4dc8-4a5a-93ec-18d3d9197374",
"question": "7d42b17d-77ff-4e0a-9a4d-354ddd7bbc57",
"score": 1
},
{
"user": "b7746016-fdbf-4f8a-9f84-05fde7b9c07a",
"question": "7d42b17d-77ff-4e0a-9a4d-354ddd7bbc57",
"score": 0
},
/* ... дополнительные данные ... */
]Заметьте, что не все пользователи правильно ответили на каждый вопрос, и результаты, в связи с этим, были отмечены как 0 либо 1.
Задача: дано некое k. Какое множество из k вопросов будет максимально коррелировать с общим показателем экзамена? Назовём это задачей k-CorrSet. Простой алгоритм перебора для решения этой задачи в виде псевдокода будет таким:
func k_corrset($data, $k):
$all_qs = all questions in $data
for all $k-sized subsets $qs within $all_qs:
$us = all users that answered every question in $qs
$qs_totals = the total score on $qs of each user in $us
$grand_totals = the grand score on $all_qs of each user in $us
$r = correlation($qs_totals, $grand_totals)
return $qs with maximum $r Далее мы реализуем несколько вариаций этого алгоритма, чтобы выяснить, насколько его можно ускорить.
▍ Основа на Python
Анализ данных я обычно начинаю с использования Python и затем уже перехожу на Rust, когда возникает потребность повысить скорость или снизить затраты памяти. Так что в качестве основы предлагаю разобрать простую программу для решения k-CorrSet, написанную с помощью Pandas:
from itertools import combinations
import pandas as pd
from pandas import IndexSlice as islice
def k_corrset(data, K):
all_qs = data.question.unique()
q_to_score = data.set_index(['question', 'user'])
all_grand_totals = data.groupby('user').score.sum().rename('grand_total')
corrs = []
for qs in combinations(all_qs, K):
qs_data = q_to_score.loc[islice[qs,:],:].swaplevel()
answered_all = qs_data.groupby(level=[0]).size() == K
answered_all = answered_all[answered_all].index
qs_totals = qs_data.loc[islice[answered_all,:]]
.groupby(level=[0]).sum().rename(columns={'score': 'qs'})
r = qs_totals.join(all_grand_totals).corr().qs.grand_total
corrs.append({'qs': qs, 'r': r})
corrs = pd.DataFrame(corrs)
return corrs.sort_values('r', ascending=False).iloc[0].qs
data = pd.read_json('scores.json')
print(k_corrset(data, K=5))В ней используется магия MultiIndex, но детали опустим. Сразу начнём тестирование. Для этого нам нужны данные. Чтобы сделать бенчмарк реалистичным, я сгенерировал синтетический датасет, который примерно соответствует реальному. Вот его характеристики:
- 60,000 пользователей;
- 200 вопросов;
- 20% незаполненности (то есть на все вопросы ответило 12,000 пользователей);
- каждый бал может с равной вероятностью быть 1 или 0.
Наша цель – вычислить для этого датасета k-CorrSet при k=5 на моём M1 MacBook Pro 2021 года за адекватный промежуток времени. Заметьте, что всего существует 2,5 миллиарда комбинаций вопросов, поэтому нужно, чтобы внутренний цикл алгоритма брутфорса был достаточно быстр.
Используя функцию Python time.time(), я вычислил скорость этого внутреннего цикла при 1,000 итераций в CPython 3.9.17. Среднее время выполнения составило 36 миллисекунд. Неплохо, но при такой скорости на общее вычисление уйдёт 2,9 года. Нужно его ускорить!
Примечание: есть разные способы ускорения кода Python, но моя цель сравнить не высоко оптимизированный код Python с высоко оптимизированным кодом Rust, а скорость вычисления «стандартного блокнота Jupyter» в Python со скоростью его высоко оптимизированной альтернативой на Rust.
▍ Перевод в Rust
Начать оптимизацию можно с повторной реализации кода Python в качестве примерно такой же программы Rust. В этом случае мы будем ожидать некоторого ускорения за счёт оптимизаций компилятора Rust. В целях читаемости весь код ниже представляет упрощение фактического бенчмарка. К примеру, я буду опускать #[derive] в типах и объединять разрозненные блоки кода в прямолинейные функции. Весь бенчмарк находится в репозитории на GitHub.
Сперва переведём типы данных:
pub struct User(pub String);
pub struct Question(pub String);
pub struct Row {
pub user: User,
pub question: Question,
pub score: u32,
}
Мы преобразуем User и Question в новые типы для ясности, и чтобы можно было реализовать для них трейты. Затем реализуем базовый алгоритм k-CorrSet так:
fn k_corrset(data: &[Row], k: usize) -> Vec<&Question> {
// utils::group_by(impl Iterator<Item = (K1, K2, V)>)
// -> HashMap<K1, HashMap<K2, V>>;
let q_to_score: HashMap<&Question, HashMap<&User, u32>> =
utils::group_by(data.iter().map(|r| (&r.question, &r.user, r.score)));
let u_to_score: HashMap<&User, HashMap<&Question, u32>> =
utils::group_by(data.iter().map(|r| (&r.user, &r.question, r.score)));
let all_grand_totals: HashMap<&User, u32> =
u_to_score.iter().map(|(user, scores)| {
let total = scores.values().sum::<u32>();
(*user, total)
})
.collect();
let all_qs = q_to_score.keys().copied();
all_qs.combinations(k)
.filter_map(|qs: Vec<&Question>| {
let (qs_totals, grand_totals): (Vec<_>, Vec<_>) = all_grand_totals.iter()
.filter_map(|(u, grand_total)| {
let q_total = qs.iter()
.map(|q| q_to_score[*q].get(u).copied())
.sum::<Option<u32>>()?;
Some((q_total as f64, *grand_total as f64))
})
.unzip();
// utils::correlation(&[f64], &[f64]) -> f64;
let r = utils::correlation(&qs_totals, &grand_totals);
(!r.is_nan()).then_some((qs, r))
})
.max_by_key(|(_, r)| FloatOrd(*r))
.unwrap().0
}Что здесь важно понять:
- Как и в случае Python, мы преобразуем плоские данные в иерархические, используя хэш-таблицу и вспомогательную функцию
utils::group_by. (Имейте ввиду, всё, что мы называемHashMap, фактически выступает псевдонимом дляfxhash::FxHashMap, которая является простоstd::collections::HashMapс более эффективным алгоритмом хэширования). - Затем мы перебираем все комбинации вопросов методом
Itertools::combinations. - Во внутреннем цикле мы перебираем всех пользователей посредством
all_grand_totals.iter(). - Выражение
q_to_score[*q].get(u).copied()имеет типOption<u32 >, который оказываетсяSome(n), если у пользователя отмечен балл дляq, иNoneв противном случае. - Итератор
.sum::<Option<u32>>()возвращаетSome(total), если пользователь ответил на все вопросы вqs, иNoneв противном случае. - Мы вызываем вспомогательный метод
utils::correlation, который реализует стандартное вычисление коэффициента корреляции Пирсона. - С помощью
max_by_keyмы получаем вопросы, максимально коррелирующие с показателем экзамена. Помимо этого, мы используемFloatOrd, чтобы иметь возможность сравнивать числа с плавающей запятой.
И какая получилась производительность? Для оценки быстродействия внутреннего цикла (filter_map) я использовал Criterion с установками по умолчанию, взяв тот же датасет. Новый внутренний цикл выполняется за 4,2 мс, что примерно в 8 раз быстрее базовой Python-версии. Но на общее вычисление при такой скорости потребуется 124 дня, что всё равно слишком долго. Пора заняться реальной оптимизацией.
▍ Индексирование данных
Вместо того чтобы гадать, как оптимизировать код, мы запустим профилировщик и посмотрим, где в нём узкие места. На своём Mac я обычно использую Instruments.app, но недавно попробовал samply и был приятно удивлён! Он гораздо удобнее. Похоже, что samply лучше работает с Rust как в плане обработки символов (demangling), так и в плане перестройки стека вызовов. Вот скриншот соответствующей части трейса samply для реализации Rust:

Около 75% всего времени выполнения код проводит в HashMap::get! А вот и виновная в этом строка кода:
q_to_score[*q].get(u).copied()Проблема в том, что мы хэшируем и сравниваем 36-байтовые строки UUID, что очень затратно. Нам нужен более компактный тип, который можно будет использовать для строк вопрос/пользователь.
Для этого мы соберём все вопросы и пользователей в Vec и представим каждую пару пользователь/вопрос по их индексу в этом Vec. Можно просто использовать индексы usize с типом Vec, но лучше будет задействовать новые типы для представления каждого вида индекса. По факту в моей работе эта проблема возникает так часто, что я уже написал для неё крейт, Indexical, взяв за основу крейт index_vec.
Эти типы индексов мы определим так:
pub struct QuestionRef<'a>(pub &'a Question);
pub struct UserRef<'a>(pub &'a User);
define_index_type! {
pub struct QuestionIdx for QuestionRef<'a> = u16;
}
define_index_type! {
pub struct UserIdx for UserRef<'a> = u32;
}
QuestionRef и UserRef – это новые типы, которые позволяют реализовывать трейты в &Question и &User. Макрос define_index_type создаёт новые типы индекса QuestionIdx и UserIdx, которые связываются с QuestionRef и UserRef. Эти индексы представлены как u16 и u32 соответственно.
Наконец, мы обновляем k_corrset, чтобы сгенерировать IndexedDomain для вопросов и пользователей, а затем на протяжении оставшейся части кода используем типы QuestionIdx и UserIdx:
fn k_corrset(data: &[Row], k: usize) -> Vec<&Question> {
// сначала создаём `IndexedDomain` для вопросов и пользователей.
let (questions_set, users_set): (HashSet<_>, HashSet<_>) = data.iter()
.map(|row| (QuestionRef(&row.question), UserRef(&row.user)))
.unzip();
let questions = IndexedDomain::from_iter(questions_set);
let users = IndexedDomain::from_iter(users_set);
// затем создаём те же структуры данных, что и раньше,
// за исключением использования `IndexedDomain::index` для поиска индексов.
// обратите внимание на изменение в типах ключей HashMap.
let q_to_score: HashMap<QuestionIdx, HashMap<UserIdx, u32>> =
utils::group_by(data.iter().map(|r| (
questions.index(&(QuestionRef(&r.question))),
users.index(&(UserRef(&r.user))),
r.score,
)));
let u_to_score: HashMap<UserIdx, HashMap<QuestionIdx, u32>> =
utils::group_by(data.iter().map(|r| (
users.index(&(UserRef(&r.user))),
questions.index(&(QuestionRef(&r.question))),
r.score,
)));
let all_grand_totals = // тот же код.
let all_qs = questions.indices();
all_qs.combinations(k)
.filter_map(|qs: Vec<QuestionIdx>| {
// тот же код.
})
.max_by_key(|(_, r)| FloatOrd(*r))
.unwrap().0
// нужно преобразовать индексы обратно в значения.
.into_iter().map(|idx| questions.value(idx).0).collect()
}Всю реализацию также можете найти на GitHub. Что касается API крейта Indexical, то он описан в документации.
Снова запускаем бенчмарк для внутреннего цикла вычислений, и теперь он выполняется за 1,0 мс, что в 4 раза быстрее предыдущей версии и в 35 раз быстрее самой первой. Итого на все вычисления сейчас у нас уйдёт уже 30 дней – продолжим!
▍ Индексирование коллекций
Повторим профилирование:

Надо же, по прежнему бо́льшую часть времени мы проводим в HashMap::get. А что, если вообще избавиться от хэш-таблиц? HashMap<&User, u32> – это, по сути, то же, что и Vec<Option<u32, где у каждого &User есть уникальный индекс. Например, в области пользователей ["a", "b", "c"] хэш-таблица {"b" => 1} равнозначна вектору [None, Some(1), None]. Для этого вектора требуется больше памяти (из-за пространств None), но он повышает скорость поиска пар ключ/значение за счёт избежания хэширования.
Мы пытаемся полностью оптимизировать производительность, и с учётом масштаба нашего датасета можем позволить себе разменять дополнительную память на прирост в скорости вычислений. Мы используем Indexical, который предоставит тип DenseIndexMap<K, V>, внутренне реализуемый как Vec<V> и индексируемый посредством K::Index.
Основное изменение функции k_corrset в том, что мы преобразуем все вспомогательные структуры данных в сжатые индексные карты:
pub type QuestionMap<'a, T> = DenseIndexMap<'a, QuestionRef<'a>, T>;
pub type UserMap<'a, T> = DenseIndexMap<'a, UserRef<'a>, T>;
fn k_corrset(data: &[Row], k: usize) -> Vec<&Question> {
// как и раньше создаём области `users` и `questions`.
// инициализируем q_to_score как пустую сжатую карту.
let mut q_to_score: QuestionMap<'_, UserMap<'_, Option<u32>>> =
QuestionMap::new(&questions, |_| UserMap::new(&users, |_| None));
// заполняем q_to_score датасетом.
for r in data {
q_to_score
.get_mut(&QuestionRef(&r.question))
.unwrap()
.insert(UserRef(&r.user), Some(r.score));
}
let grand_totals = UserMap::new(&users, |u| {
q_to_score.values().filter_map(|v| v[u]).sum::<u32>()
});
let all_qs = questions.indices();
all_qs.combinations(k)
// почти тот же код, см. ниже
}Единственное изменение внутреннего цикла в том, что наш код, который выглядел так:
q_to_score[*q].get(u).copied()Теперь выглядит так:
q_to_score[*q][u]Повторение бенчмарка показывает, что теперь внутренний цикл выполняется за 181 мкс, то есть в 6 раз быстрее последней версии и в 199 раз быстрее Python-версии. Нам удалось сократить общее время вычисления до 5,3 дня.
▍ Контроль границ
Ещё один удар по быстродействию наносит каждое использование квадратных скобок для индексирования DenseIndexMap. Приведённый ниже вектор выполняет проверку границ, но наш код в его текущем виде гарантированно никогда не выйдет за границы вектора. Я не смог найти эту проверку в выводе samply, но она значительно влияет на бенчмарк, а значит, её стоит убрать.
До этого наш внутренний цикл выглядел так:
let q_total = qs.iter()
.map(|q| q_to_score[*q][u])
.sum::<Option<u32>>()?;
let grand_total = all_grand_totals[u];
После удаления проверки с помощью get_unchecked наш внутренний цикл принял такой вид:
let q_total = qs.iter()
.map(|q| unsafe {
let u_scores = q_to_score.get_unchecked(q);
*u_scores.get_unchecked(u)
})
.sum::<Option<u32>>()?;
let grand_total = unsafe { *all_grand_totals.get_unchecked(u) };
Без проверки выхода за границы цикл оказывается небезопасным, поэтому мы помечаем блоки как unsafe.
При очередном выполнении бенчмарка внутренний цикл занимает 156 мкс, что в 1,16 раза быстрее последнего варианта и в 229 раз быстрее базовой Python-версии. Теперь на все вычисления потребуется 4,6 дня.
▍ Битовые карты
На данный момент мы добились ускорения в 225 раз, а значит, нам ещё предстоит улучшить результат почти на три порядка. Для этого нужно переосмыслить структуру внутреннего цикла.
Сейчас он, по сути, выглядит так:
for each subset of questions $qs:
for each user $u:
for each question $q in $qs:
if $u answered $q: add $u's score on $q to a running total
else: skip to the next user
$r = correlation($u's totals on $qs, $u's grand total)Важная особенность наших данных в том, что они формируют разрежённую матрицу. На любой отдельно взятый вопрос лишь 20% пользователей дали ответ. Если брать 5 произвольных вопросов, то на них ответ дало ещё меньшее число людей. Поэтому если мы сможем эффективно сначала определять, какие пользователи ответили на все 5 вопросов, то итоговый цикл будет выполнять меньше итераций (и освободится от ветвлений). Что-то вроде такого:
for each subset of questions $qs:
$qs_u = all users who have answered every question in $qs
for each user $u in $qs_u:
for each question $q in $qs:
add $u's score on $q to a running total
$r = correlation($u's scores on $qs, $u's grand total)
Как же нам представить множество пользователей, ответивших на конкретный вопрос? Можно использовать HashSet, но мы уже видели, что хэширование вычислительно затратно. Поскольку наши данные индексированы, можно использовать более эффективную структуру битовой карты, в которой с помощью отдельных битов памяти выражается присутствие или отсутствие объекта. Indexical предоставляет ещё одну абстракцию для интеграции битовых карт с нашими индексами нового типа: IndexSet.
Ранее наша структура данных q_to_score представляла отображение вопросов в индексированный по пользователям вектор баллов (то есть, UserMap<'_, Option<u32>>). Теперь мы изменим Option<u32> на u32 и добавим битовую карту, описывающую множество пользователей, ответивших на конкретный вопрос. Первая половина изменённого кода будет выглядеть так:
type UserSet<'a> = IndexSet<'a, UserRef<'a>>;
let mut q_to_score: QuestionMap<'_, (UserSet<'_>, UserMap<'_, u32>)> =
QuestionMap::new(&questions, |_| (
UserMap::<'_, u32>::new(&users, |_| 0),
UserSet::new(&users),
));
for r in data {
let (scores, set) = &mut q_to_score.get_mut(&QuestionRef(&r.question)).unwrap();
scores.insert(UserRef(&r.user), r.score);
set.insert(UserRef(&r.user));
}
Заметьте, что q_to_score теперь, по сути, содержит недействительные значения, так как мы устанавливаем 0 для тех, кто на вопрос не ответил. Нам нужно остерегаться использования в вычислениях недействительных значений.
Далее мы обновляем внутренний цикл, чтобы он соответствовал новому псевдокоду:
let all_qs = questions.indices();
all_qs.combinations(k)
.filter_map(|qs: Vec<QuestionIdx>| {
// вычисляем пересечение множеств пользователей для каждого вопроса.
let mut users = q_to_score[qs[0]].1.clone();
for q in &qs[1..] {
users.intersect(&q_to_score[*q].1);
}
let (qs_totals, grand_totals): (Vec<_>, Vec<_>) = users.indices()
// только .map, а не .filter_map, как раньше.
.map(|u| {
let q_total = qs.iter()
.map(|q| unsafe {
let (u_scores, _) = q_to_score.get_unchecked(q);
*u_scores.get_unchecked(u)
})
// только u32, а не Option<u32>, как раньше.
.sum::<u32>();
let grand_total = unsafe { *all_grand_totals.get_unchecked(u) };
(q_total as f64, grand_total as f64)
})
.unzip();
let r = utils::correlation(&qs_totals, &grand_totals);
(!r.is_nan()).then_some((qs, r))
})
// остальной код прежний.Снова выполняем бенчмарк и видим, что внутренний цикл обрабатывается за 47 мкс – то есть в 3,4 раза быстрее последнего варианта и в 769 раз быстрее изначальной реализации Python. Теперь мы сократили общее время вычисления до 1,4 дня.
▍ SIMD
Новая вычислительная структура определённо всё ускорила, но пока что недостаточно. Повторим проверку с помощью samply:

Теперь код всё основное время проводит за вычислением пересечений битовых карт. Это означает, что нам нужно заглянуть в реализацию соответствующей библиотеки. В качестве такой библиотеки для работы с битовыми картами Indexical использует bitvec. На 2023 год реализация метода intersect в ней выглядит примерно так:
fn intersect(dst: &mut BitSet, src: &BitSet) {
for (n1, n2): (&mut u64, &u64) in dst.iter_mut().zip(&src) {
*n1 &= *n2;
}
}
Значит, bitvec выполняет AND для одного элемента u64 за раз. Но, как оказывается, в большинстве процессоров есть инструкции SIMD (Single Instruction stream, Multiple Data stream, одна команда – множество потоков данных), предназначенные для манипуляции с битами в нескольких элементах u64 одновременно. К счастью, в Rust предлагается экспериментальный API SIMD std::simd, который мы и используем. В примерном виде версия SIMD для вычисления пересечений битовых карт выглядит так:
fn intersect(dst: &mut SimdBitSet, src: &SimdBitSet) {
for (n1, n2): (&mut u64x4, &u64x4) in dst.iter_mut().zip(&src) {
*n1 &= *n2;
}
}
Единственное отличие в том, что мы заменили примитивный тип u64 типом SIMD u64x4, и внутренне Rust создаёт одну инструкцию SIMD для выполнения операции &=, обрабатывающей четыре элемента u64 одновременно.
А где нам взять BitSet, ускоренный с помощью SIMD? Bitvec не поддерживает SIMD. На crates.io есть несколько решений, и я попробовал одно из них под названием bitsvec. Для быстрого вычисления пересечений подходит отлично, но используемый в этом крейте итератор, отвечающий за поиск индексов битов 1, оказался медленным. Поэтому я скопировал основные куски bitsvec и написал более эффективный итератор, с которым вы можете ознакомиться в исходном коде Indexical.
Благодаря абстракциям Indexical, для подстановки битовых карт, обрабатываемых с помощью SIMD, потребуется лишь изменить псевдоним типов в функции k_corrset. Я экспериментировал с разными размерами линий векторов, и на моей машине с этим датасетом самым эффективным оказался u64x16.
Снова запускаем бенчмарк, и наш цикл выполняется за 1,35 мкс, то есть в 34 раза быстрее последней версии и в 26,459 раз быстрее самой первой. Общее время вычисления сократилось до 57 минут.
▍ Выделение памяти
Мы уже приблизились к пиковой производительности. (Вам это может не понравиться, но…) Вернёмся к данным профилировщика и на этот раз рассмотрим их инвертированное представление (в котором отражены самые часто вызываемые функции в листовых узлах дерева вызовов):
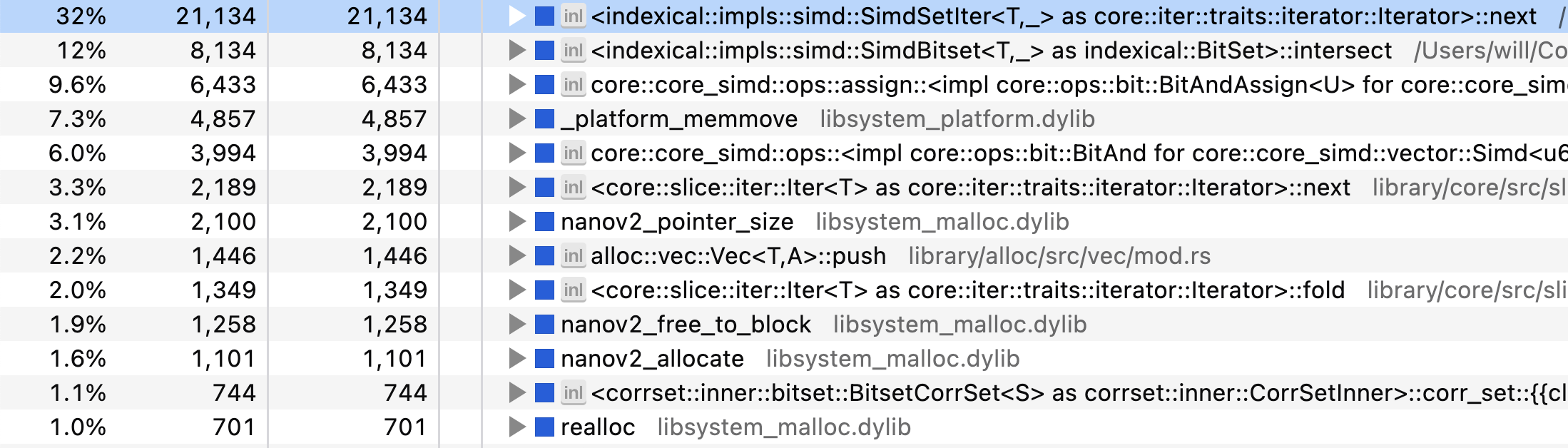
Самое узкое место – это итератор битовых карт. Серьёзно! Но здесь ещё есть ряд связанных функций: memmove, realloc, allocate — всё верно, мы выделяем во внутреннем цикле итератора память. В частности, здесь есть битовая карта пользователей, которую мы изначально клонируем, и есть два вектора для qs_totals и grand_totals, которые мы выделяем с помощью unzip.
Чтобы избежать выделения, мы создаём эти структуры данных заранее с максимально необходимым размером и затем циклически производим в них запись:
// заблаговременное выделение данных.
let mut qs_totals = vec![0.; users.len()]
let mut grand_totals = vec![0.; users.len()];
let mut user_set = IndexSet::new(&users);
let all_qs = questions.indices();
all_qs.combinations(k)
.filter_map(|qs| {
// используем `clone_from` вместо `clone`, чтобы выполнить копирование без выделения.
user_set.clone_from(&q_to_score[qs[0]].1);
for q in &qs[1..] {
user_set.intersect(&q_to_score[*q].1);
}
let mut n = 0;
for (i, u) in user_set.indices().enumerate() {
let q_total = qs.iter()
.map(|q| unsafe {
let (u_scores, _) = q_to_score.get_unchecked(q);
*u_scores..get_unchecked(u)
})
.sum::<u32>();
let grand_total = unsafe { *all_grand_totals.get_unchecked(u) };
// обновляем totals/grand_totals на месте без передачи в вектор.
unsafe {
*qs_totals.get_unchecked_mut(i) = q_total as f64;
*grand_totals.get_unchecked_mut(i) = grand_total as f64;
}
n += 1;
}
// передаём только первые `n` элементов!
let r = utils::correlation(&qs_totals[..n], &grand_totals[..n]);
(!r.is_nan()).then_some((qs, r))
})Повторяем бенчмарк и видим, что внутренний цикл ускорился до 1,09 мкс, что в 1,24 раза быстрее прошлой версии и в 32,940 раз быстрее основы на Python. Теперь на общее вычисление уйдёт всего 46 минут.
Впечатляет, что аллокатор кучи оказался достаточно быстр и повлиял на время выполнения совсем незначительно.
В таблице 1 представлена сводка, отражающая время выполнения, относительное ускорение и примерное общее время для каждого уровня бенчмарка.
Таблица 1: Показатели быстродействия для внутреннего цикла:
| Уровень | Время выполнения | Ускорение относительно прошлого уровня | Ускорение относительно Python | Оценочное время полного завершения |
| Python | 35.85 мс | 1.00× | 2.88 лет | |
| 0_basic | 4.24 мс | 8.46× | 8.46× | 124.40 дня |
| 1_indexed | 1.03 мс | 4.11× | 34.78× | 30.25 дня |
| 2_imap | 180.52 мкс | 5.71× | 198.60× | 5.30 дня |
| 3_bchecks | 156.23 мкс | 1.16× | 229.47× | 4.59 дня |
| 4_bitset | 46.60 мкс | 3.35× | 769.26× | 1.37 дня |
| 5_simd | 1.35 мкс | 34.40× | 26,459.54× | 57.26 мин |
| 6_alloc | 1.09 мкс | 1.24× | 32,940.02× | 45.99 мин |
Достигнутое абсолютное ускорение отражено на рисунке ниже. Обратите внимание, что ось y представлена в логарифмическом масштабе.
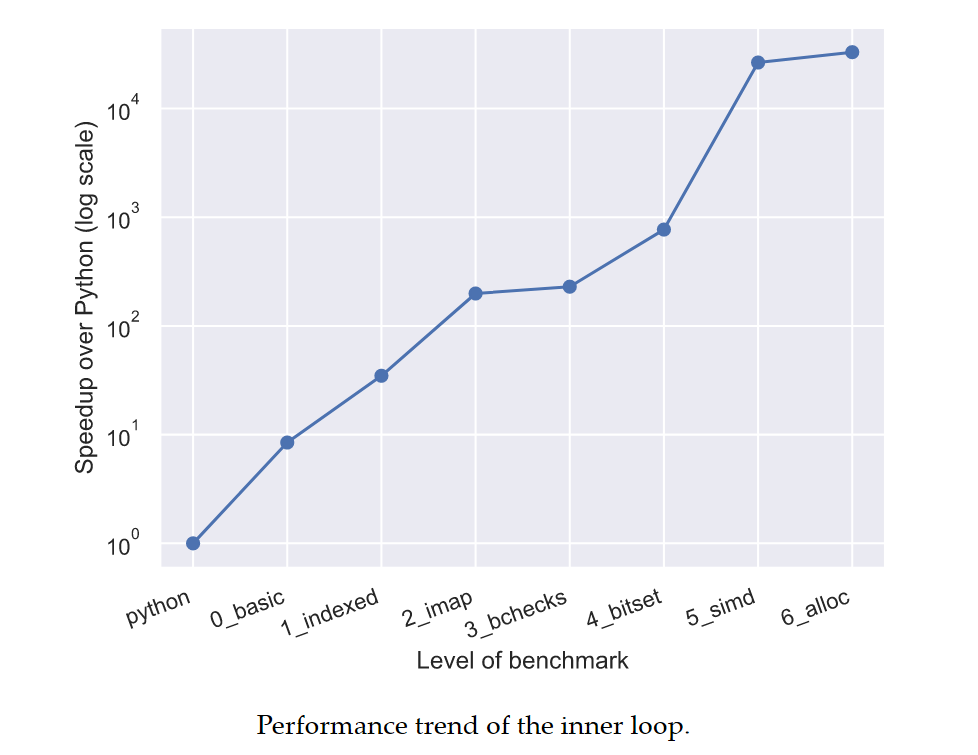
Тренд изменения производительности внутреннего цикла
▍ Параллелизм
К этому моменту мы, казалось бы, полностью исчерпали доступные для оптимизации средства. Лично я не могу придумать какие-либо ещё приёмы для ощутимого ускорения внутреннего цикла – напишите в комментариях, если у вас есть идеи на этот счёт. Но у нас остался ещё один, теперь уже последний, приём – параллелизм. Эта задача крайне параллельна, а значит можно с лёгкостью распределить выполнение внутреннего цикла по нескольким ядрам. С помощью Rayon это делается на раз:
let all_qs = questions.indices();
all_qs.combinations(k)
.par_bridge()
.map_init(
|| (vec![0.; users.len()], vec![0.; users.len()], IndexSet::new(&users)),
|(qs_totals, grand_totals, user_set), qs| {
// тот же код, что и раньше.
})
// тот же код, что и раньше.
Метод par_bridge получает последовательный итератор и преобразует его в параллельный. Функция map_init представляет параллельную карту с соответствующим потоку состоянием, поэтому мы по-прежнему обходимся без выделения.
Для оценки внешнего цикла нам нужен другой бенчмарк. Я выполнил этот цикл для обработки 5,000,000 комбинаций вопросов за раз с помощью Criterion, используя заданную стратегию. Этого количества выполнений достаточно, чтобы обнаружить отличия в каждом внешнем цикле без многонедельного ожидания завершения бенчмарка.
Выполнение теста с использованием последовательной стратегии для самого быстрого внутреннего цикла занимает 6,8 секунд. В моём MacBook Pro 10 ядер, значит при использовании Rayon можно ожидать примерно 10-кратного ускорения. После анализа этой параллельной стратегии мы получаем 4,2 секунды на вычисление 5,000,000 комбинаций. Ускорение составило всего 1,6 раза. Позор!
▍ Группирование
Вернёмся к профилировщику, чтобы найти причину проблем с масштабированием:

Наши потоки бо́льшую часть времени проводят за блокированием и разблокированием мьютекса. Получается, у нас есть проблемы с синхронизацией. Действительно, если внимательно прочесть документацию к par_bridge, то мы найдём ключевое предложение:
Итерируемые элементы по одному извлекаются функцией
next()из каждого готового к работе потока синхронизировано, в связи с чем этот процесс может стать узким местом, если последовательный итератор не будет поспевать за параллельным спросом со стороны потоков.
Похоже, что процесс передачи между итератором Itertools::combinations и параллельным мостом Rayon слишком медленный. Учитывая, что у нас есть огромное число комбинаций, простым способом избежания этого узкого места будет более детальное присваивание задач. То есть мы можем объединять вместе множество комбинаций вопросов и передавать их в поток одновременно.
Для этого я наскоро набросал группирующий итератор, который использует ArrayVec для избежания выделения.
pub struct Batched<const N: usize, I: Iterator> {
iter: I,
}
impl<const N: usize, I: Iterator> Iterator for Batched<N, I> {
type Item = ArrayVec<I::Item, N>;
#[inline]
fn next(&mut self) -> Option<Self::Item> {
let batch = ArrayVec::from_iter((&mut self.iter).take(N));
(!batch.is_empty()).then_some(batch)
}
}Затем мы изменим внешний цикл, добавив группировку в итератор комбинаций, и внутренний, чтобы тот уплощал каждый пакет:
let all_qs = questions.indices();
all_qs.combinations(k)
.batched::<1024>()
.par_bridge()
.map_init(
|| (vec![0.; users.len()], vec![0.; users.len()], IndexSet::new(&users)),
|(qs_totals, grand_totals, user_set), qs_batch| {
qs_batch
.into_iter()
.filter_map(|qs| {
// тот же код, что и раньше.
})
.collect_vec()
})
.flatten()
// тот же код, что и раньше.Снова повторяем бенчмарк внешнего цикла, и теперь группирующий итератор обрабатывает 5,000,000 комбинаций за 982 мс. Это в 6,9 раза быстрее последовательного подхода, что уже гораздо лучше для моей 10-ядерной машины. В идеале мы бы приблизились к 10-кратному ускорению, но я думаю, статья и без того получилась достаточно большой. Сводка показателей выполнения внешнего цикла приведена в таблице 2.
Таблица 2: показатели производительности внешнего цикла:
| Уровень | Время выполнения | Ускорение относительно предыдущей версии | Ускорение относительно Python | Оценочное время завершения |
| 0_serial | 6.80 с | 26,342.63× | 57.51 мин | |
| 1_parallel | 4.22 с | 1.61× | 42,439.31× | 35.70 мин |
| 2_batched | 982.46 мс | 4.30× | 182,450.94× | 8.30 мин |
▍ Заключение
Чего же мы достигли? При k=5 исходной программе Python потребовалось бы 2,9 года для завершения. Итоговой же программе Rust на обработку того же датасета нужно всего 8 минут. То есть мы добились ускорения почти в 180,000 раз. Какие основные оптимизации мы применили:
- оптимизации компилятора Rust;
- хэш-числа вместо строк;
- (индексированные) векторы вместо хэш-таблиц;
- битовые карты для эффективного тестирования принадлежности;
- SIMD для эффективной обработки пересечений битовых карт.
- Многопоточность для разделения работы по нескольким ядрам;
- группировку для избежания возникновения узкого места при распределении работы;
Можно ли добиться большего? Сформируем последний профиль:
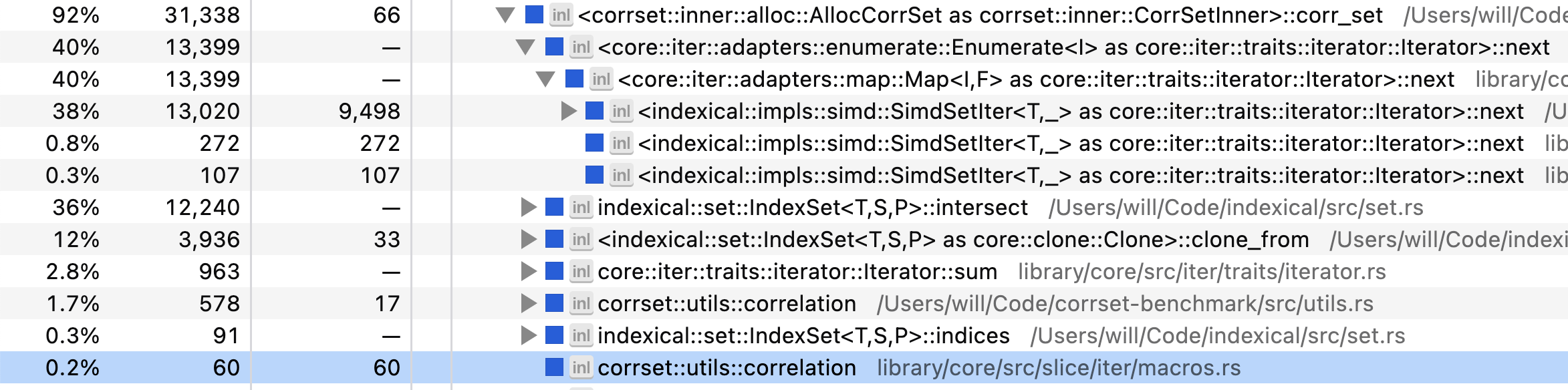
Код 38% времени проводит в итераторе битовых карт и 36% за вычислением пересечений этих карт. Ещё 12% уходит на копирование изначальной битовой карты для заданного множества вопросов. Ещё остаётся длинный хвост других операций вроде вычисления корреляции.
Я приложил все усилия, чтобы ускорить реализацию вычисления битовых карт с помощью SIMD, поэтому не знаю, как ещё можно улучшить эти показатели. Можно получить +10% к скорости за счёт точечной подстройки различных констант (размера линий векторов, размера пакетов и так далее), но я не думаю, что удастся продвинуться ещё на целый порядок. Если у вас есть идеи, приглашаю их опробовать: github.com/willcrichton/corrset-benchmark
Кроме того, если вам известно аналитическое решение этой задачи, то есть более грамотный способ получить оптимальный ответ без брутфорса, обязательно сообщите. А так надеюсь, что в статье вы нашли для себя что-то новое в контексте оптимизации производительности в Rust.
Автор: Дмитрий Брайт