Добро времени суток. Хочу рассказать о том, как я создавал велосипед для подсчета рейтинга в списке объектов на основе данных о визитах и хитах.
Предметная область
- имеется веб-ресурс — каталог некоторых сущностей
- сущности разделены на группы/каталоги
- у каждый сущности могут быть фото, видео, отзывы, контактные данные
- в разных категориях сущностей разные средние посещения и просмотры, последние обозначим "k"
Требования
Необходимо внедрить алгоритм сортировки внутри категорий сущностей, который зависит следующих переменных:
- визиты сущности. Составной ключ: день + ip + id + дополнительное_поле:= «index»
- визиты страницы с видео. Составной ключ: день + ip + id + дополнительное_поле:= «video»
- визиты страницы с аудио. Составной ключ аналогично визиту для видео
- визиты страницы с фото. Составной ключ аналогично визиту для видео
- просмотры по аналогичным параметрам
- "k" — среднее количество просмотр в каталоге за единицу времени
Фактически, визит — одна запись в таблице визитов, а просмотр — это счетчик обновляемый следующим запросом в бд:
INSERT INTO `visit` (pEssence, pMethod, tEssense, ip, ddDateCreated)
VALUES ("%s", "%s", %d, "%s", "%s")
ON DUPLICATE KEY UPDATE pViewsCount = pViewsCount + 1;
Причем, все визиты должны влиять на рейтинг линейно, но при росте числа просмотров скорость роста рейтинга(производная) должна замедляться, а просмотр страницы с контактами сущности должен поднимать рейтинг в два раза быстрее.
С линейными параметрами всё ясно, а для просмотров нужна формула разная для каждого каталога, которая зависит от нашего k, т.е до достижения параметра k количество просмотров «почти линейно» должно влиять на рейтинг, а после «утрачивать свое влияние». Первым в голову пришли логарифм и функция квадратного корня. Я выбрал логарифм.
Ход работы
f(x) = ln(x)
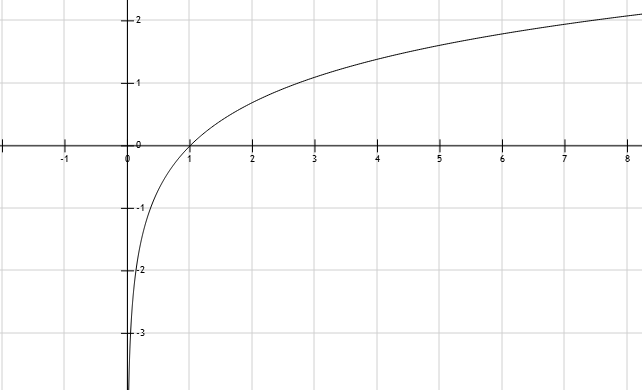
Здесь видно, что на отрезке x:[1; 2] и x:[2; +infinity] график ведет почти так, как нам нужно — остается только изменить его масштаб, переместить пересечение с осью x в точку [0,0], подобрать коэффициент так, чтобы график попал в точку [k, k].
Чтобы адаптировать его под параметр k нужно будет произвести несколько преобразований:
Для наглядности возьмем k=10
Растянем график в k раз и переместим пересечение с осью x в точку [0,0]:
f(k, x)|k:=10 = 10 + 10*ln((10+x)/(10*e))
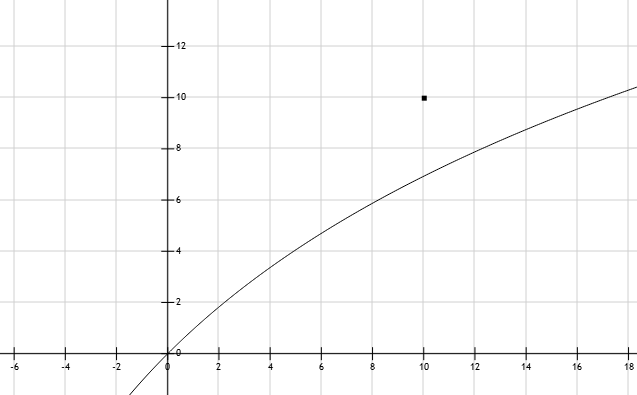
Осталось подобрать коэффициент j:
f(k, k)*j = k => j = k/f(k, k)
j — константа, равная 1.44269504089
Интересно, что же это за число? Wolframalpha подсказывает, что это 1/ln(2), за что ему спасибо.
В итоге конечная формула имеет вид:
f(k, x) = (k + k*ln((x+k)/(k*e)))*(1.44269504089) или f(k, x) = (k + k*ln((x+k)/(k*e)))/ln(2)
Для оптимизации под бд, с помощью того же Wolframalpha, уменьшим количество умножений, делений и выделим константы:
c1(k) = k*ln(k)
c2 = 1.4426950408889634
f(k, x) = (k*ln(k + x)-c1(k))*c2
f(k, x)|k:=10
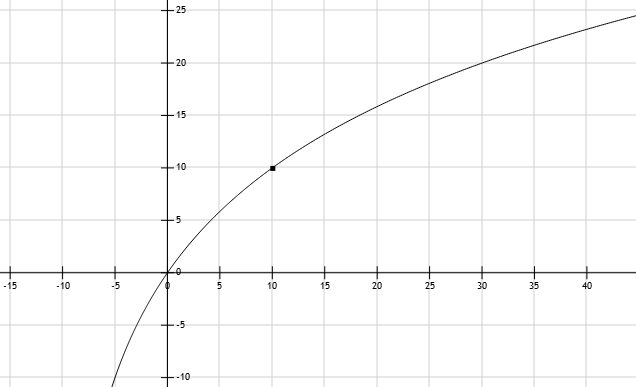
Что и требовалось получить.
Защита рейтинга
Первое что нужно сделать — выдавать заголовок для всех рейтинговых страниц «X-FRAME-OPTIONS: DENY» чтобы рейтинг не накручивался через i-фреймы.
Второе — это ввод геофильтра ip-адресов. В моем случае мне нужно было отсечь все адреса, которые не относятся к двум нашим мегаполисам и к их областям.
Третье — посещения записывать только с помощью javascript, чтобы осложнить работу ленивым накрутчикам. Соответственно необходимо обфусцировать сам скрипт, обфусцировать его выдачу (выдавать в случайные места страницы), создать ложные выдачи, написать генератор обфусцированного javascript-кода, обфусцировать URI приёмника запроса на обновление статистики, т.е лучше всего его сделать динамическим, который зависеть от ip-адреса и текущей даты
Идеальную защиту придумать здесь будет трудно, но так мы отнимем некоторое время на анализ защиты и отсеим ленивую/дешевую рабочую силу.
Использованные реусрсы
fooplot.com — построение графиков
wolframalpha.com — математические преобразования
Автор: frostosx






