Мои читатели — занятые люди, поэтому сразу перейду к делу. Вот она, самая быстрая обобщённая (и простая) реализация двоичного поиска на C++:
template <class ForwardIt, class T, class Compare>
constexpr ForwardIt sb_lower_bound(
ForwardIt first, ForwardIt last, const T& value, Compare comp) {
auto length = last - first;
while (length > 0) {
auto rem = length % 2;
length /= 2;
if (comp(first[length], value)) {
first += length + rem;
}
}
return first;
}
Тот же интерфейс функции, что и у std::lower_bound, но вдвое быстрее и короче. «Без ветвления», потому что if компилируется в команду условной передачи, а не в ветвление/условный переход. Ближе к концу статьи мы изучим опции компилятора и даже более быстрые версии полностью без ветвления. Для понимания этой статьи не нужны особые знания в C++. Достаточно понимать, что итераторы (first и last) по сути являются указателями на элементы массива, хотя могут указывать на один элемент дальше, чем последний элемент массива. Можете не обращать внимания на template, class, constexpr и &. Вот если бы существовал быстрый и чистый язык, работающий на уровне железа...1 2
Введение в двоичный поиск
У нас имеется отсортированный список, и нам нужно найти, куда можно вставить value. В C++ для этого используется std::lower_bound, возвращающая первую позицию (итератор), для которой сравнение (обычно <) возвращает false, или last, если сравнение истинно для всех элементов.
Двоичным поиск назван потому, что разделяет список на две части по какому-то среднему элементу, а затем выполняет сравнение среднего с нужным значением value. Исходя из результатов сравнения, мы выбираем один из двух списков, в котором будем продолжать поиск. Мы начинаем со списка с некой длиной length = last - first, начинающегося с заданного итератора first. Нам нужен цикл, чтобы продолжать исполнение, пока список не окажется пустым, то есть while (length > 0). Выбираем середину в length / 2, выполняем сравнение и обновляем текущий список, что происходит при помощи изменения first и length. Вот так:
// std_lower_bound()
auto length = last - first;
while (length > 0) {
auto half = length / 2;
if (comp(first[half], value)) {
first += half + 1;
length -= half + 1;
} else {
length = half;
}
}
return first;Всё просто. Мы получили слегка отрефакторенную версию, которая используется в gcc/libstdc++, или в llvm/libc++. Они имеют примерно одинаковую скорость и даже компилируются (иногда) в один и тот же ассемблерный код в цикле.
Прогнозирование ветвления
«Что же в этом коде медленного?» Почти ничего, но я рад, что вы спросили. Отличный вопрос. За долгие годы развития процессоры становились всё быстрее и быстрее, в том числе и благодаря прогнозированию ветвления. Краткое объяснение: для ускорения работы CPU пытается исполнять команды параллельно, разделяя исполнение каждой команды на несколько этапов, допустим, F-D-E-W (fetch, decode, execute, writeback — получение, декодирование, исполнение, запись обратно). При правильном проектировании он может одновременно выполнять вычисления на нескольких этапах разных команд (например: команда 5 на этапе F, 6 — на этапе D, 7E, 8F). Трудности возникают в случае наличия в коде ветвлений, например, команд условного перехода, когда в зависимости от некого результата следующей командой должна быть X или Y. CPU прогнозирует один вариант, X, и начинает поэтапное выполнение, постепенно добавляя этапы, допустим, X+1 и X+2. Когда результат будет готов, но окажется, что нужно было выполнить команду Y, то результаты выполнения X, X+1 и X+2 становятся бессмысленными и выбрасываются. Ошибочные прогнозы ветвления затратны, поскольку CPU мог вместо них выполнить расчёты Y, Y+1 и Y+2.
Прогнозирование ветвлений — отличная вещь, но не для двоичного поиска. Это поиск, а ищем мы только то, местонахождения чего точно не знаем, в противном случае мы бы просто взяли нужное. Это значит, что if (comp(first[half], value)) непредсказуемо при обычном применении std::lower_bound.

«Мои прогнозы ошибочны только в половине случаев!»
Давайте поможем процессору.
Мы говорим:
// bstd_lower_bound()
auto length = last - first;
while (length > 0) {
auto half = length / 2;
bool compare = comp(first[half], value);
// if больше нет
first = compare ? first + half + 1 : first;
length = compare ? length - half - 1 : half;
}
return first;Компилятор Clang: «Нет, это так не работает!»
Мы: -mllvm -x86-cmov-converter=false
Компилятор Clang: «Как скажете, босс»3.
Результат на 25% быстрее, потому что использует две команды условной передачи. Неплохо. Но оказывается, что -mllvm -x86-cmov-converter=false, который мы сократим до -cmov, настолько же ускоряет std::lower_bound, потому что clang достаточно умён, чтобы понять, как преобразовать if/else в условную передачу. У gcc нет такой опции, и обычно его не волнует, что нам нужно.
В целом пока нет удобного способа узнать, будет ли clang4 или gcc5 использовать условную передачу в конкретном случае. Но я пишу статью не об особенностях компиляторов, так что давайте двигаться дальше.
С чего всё началось
Почему мы вообще обсуждаем ускорение двоичного поиска? Зачем я втягиваю вас в это? Потому что меня самого в это втянули.
Я увидел, как Малте Скарупке преобразовал алгоритм Шора в двоичный поиск на C++ (branchless_lower_bound), и не мог отделаться от мысли, что он неоптимален. Версия Малте иногда несколько раз сравнивает value с одним и тем же элементом. Поэтому я задался вопросом, каким же будет оптимальный двоичный поиск без ветвления? Это привело меня к созданию sb_lower_bound, который примерно на 20% быстрее, чем версии lower_bound Малте, по его тестам оказавшаяся вдвое быстрее, чем у GCC.
«Что вообще такое „оптимальный“ двоичный поиск?» Хороший вопрос. Думаю, что двоичный поиск «оптимален», если он выполняется за минимальное количество сравнений. Это очень полезно, если функция сравнения (относительно) медленная. Малте отметил, что его версия медленнее, чем std::lower_bound при двоичном поиске в большом количестве строк.
Взглянув на std::lower_bound, мы увидим, что она возвращает итератор, который может указывать на любой из элементов списка, но также на один элемент за его концом. Для списка размером n существует n+1 возможных вариантов. То есть для списка размером 2k-1 существует 2k возможных вариантов. В таком случае оптимальное количество сравнений равно k. Это можно доказать, поскольку возможность провести различие между всеми 2k вариантами требует k битов информации, а каждое сравнение даёт нам 1 бит информации (true или false). Преобразовав этот случай в код, мы получим:
// Очень быстро, но работает, когда длина равна степени двойки минус 1
// В противном случае это может привести к доступу out of bounds, например, для
// массива [0, 1, 2, 3, 4, 5] и значения 4
auto length = last - first;
while (length > 0) {
length /= 2;
if (comp(first[length], value)) {
first += length + 1;
}
}
return first;
При clang -cmov цикл компилируется в 6 команд, одной из которых является cmov. Этот код (и код Малте) настолько быстр, потому что от результата сравнения зависит только изменение first.
sb_lower_bound
Теперь давайте рассмотрим sb_lower_bound (название дано от simple branchless, «простой алгоритм без ветвления»). На самом деле, я наткнулся на него позже, чем на более быстрые версии (о которых будет рассказано ниже), потому что он не «оптимален».
auto length = last - first;
while (length > 0) {
auto rem = length % 2;
length /= 2;
if (comp(first[length], value)) {
first += length + rem;
}
}
return first;
Каждый раз, когда мы разбиваем список, и количество элементов оказывается чётным, а comp возвращает true, то мы не пропускаем достаточное количество элементов. Для n элементов, где 2k <= n < 2k+1 алгоритм sb_lower_bound всегда будет выполнять k+1 сравнений, а std::lower_bound будет выполнять или k, или k+1 сравнений. В среднем std::lower_bound будет делать примерно log2(n+1) сравнений. В целом sb_lower_bound быстрее, потому что у него в цикле гораздо меньше команд. Чтобы различие между количеством сравнений k+1 и log2(n+1) оказалось существенным, функция сравнения должна быть очень медленной.
Вторая тонкость заключается в том, сейчас вне зависимости от уровня оптимизации gcc не создаёт для sb_lower_bound код без ветвления. Для std::lower_bound он тоже не создаёт код без ветвления, поэтому в конечном итоге он оказывается столь же быстрым. Мы можем попробовать написать встроенный ассемблерный код, чтобы вынудить gcc использовать cmov, но тут возникает недостаток. При простом решении получается больше команд, чем необходимо. Альтернатива требует написания разного ассемблерного кода для каждого возможного типа value (int, float и так далее).
auto length = last - first;
while (length > 0) {
auto rem = length % 2;
length /= 2;
auto firstplus = first + length + rem;
// Выполняет сравнение, задающие x86 FLAGS наподобие CF или ZF
bool compare = comp(first[length], value);
// Встроенный ассемблерный код не поддерживает передачу bool напрямую во FLAGS
// поэтому мы просим компилятор скопировать их из FLAGS в регистр
__asm__(
// Затем мы тестируем регистр, который присваивает ZF=!compare и CF=0
// Ссылка: https://www.felixcloutier.com/x86/test
"test %[compare],%[compare]n"
// cmova копирует firstplus first, если ZF=0 и CF=0
// Ссылка: https://www.felixcloutier.com/x86/cmovv
"cmova %[firstplus],%[first]n"
: [first] "+r"(first)
: [firstplus] "r"(firstplus), [compare]"r"(compare)
);
}
return first;
В два раза быстрее, чем gcc-версия std::lower_bound, но немного медленнее, чем sb_lower_bound с clang -cmov. Показываю это просто для демонстрации.
▍ Более оптимально
Во введении я обещал показать ещё более быструю версию. Вот она:
// bb_lower_bound
auto length = last - first;
// пока length не является степенью двойки минус 1
while (length & (length + 1)) {
auto step = length / 8 * 6 + 1; // МАГИЯ
if (comp(first[step], value)) {
first += step + 1;
length -= step + 1;
} else {
length = step;
break;
}
}
while (length != 0) {
length /= 2;
if (comp(first[length], value)) {
first += length + 1;
}
}
return first;
Давайте вкратце разберём length & (length + 1). Пример: length равна 110011, length+1 равна 110100, length & (length+1) равно 110000. Обратите внимание, что они всегда имеют один общий самый старший бит 1, за исключением случая, когда length+1 выполняет перенос всех битов со значением 1. Это случай, когда length имеет вид 11..1, то есть степень двойки минус 1, и в таком случае length & (length + 1) будет равно 0. Эта методика является адаптацией одного из трюков с жонглированием битами, которые я помню. Осторожно, здесь есть целая куча потрясающих трюков.
Давайте называть length «хорошей», если она является степенью двойки минус 1. Выше мы выяснили, что для хороших длин можно выполнять оптимальный поиск. Изначальная идея заключалась в том, чтобы в случае неудобной длины мы бы разбивали список поиска не пополам, а так, чтобы быстро прийти к поиску только по подспискам хорошей длины. Эта идея была недостаточно быстрой, потому что нам бы пришлось тратить много времени только на разбиение списка. Первый компромисс заключается в этом раннем break, означающем, что второй цикл while может (неоптимально) выполнять поиск за пределами своей исходной длины; но доступ out of bounds не выполняется, потому что этот подсписок не находится в конце полного списка. Этот компромисс приводит ко второму компромиссу, но МАГИЯ заключается в выборе размера step. Для быстрого выполнения step должен быть большим, конкретно >= length/2, потому что мы чаще выходим к более быстрому циклу while. Но не настолько большим, чтобы step был почти равен length, потому что мы потеряем то, что делает двоичный поиск быстрым. Также мы бы предпочли, чтобы step был «хорошим» или имел много единиц в своём двоичном виде, что делает второй цикл while более оптимальным. Именно множество единиц заставляет step быть нечётным. И последнее: мы хотим, чтобы length - step - 1 было «хорошим».
Я попробовал довольно много вариаций. Самой привлекательной была auto step = length >> 1; step |= step >> 1;; я рассчитывал, что это будет хорошая быстрая эвристика, балансирующая перечисленные выше компромиссы, она очень близка к оптимальной, но в конечном итоге оказалась немного медленнее МАГИИ. Ещё одна проблема заключается в том, что из «break» в ней появляется ветвление.
Ещё одна неисследованная возможность заключается в полном поиске самых быстрых (но всё равно оптимальных) значений step для каждой длины и в сохранении их в таблицу. Потом можно извлечь из этой таблицы хорошую эвристику, или использовать её напрямую. В случае с sb_lower_bound я нашёл свою достаточно хорошую точку, но вы можете исследовать этот вопрос глубже.
auto length = last - first;
while (length & (length + 1)) {
auto step = precomputed[length];
if (comp(first[step], value)) {
first += step + 1;
length -= step + 1;
} else {
length = step;
}
}Чем меньше ветвлений, тем лучше?
Если вкратце, то нет. Этот раздел можно пропустить, но вот более развёрнутый ответ: для n элементов, где 2k <= n < 2k+1, алгоритм sb_lower_bound всегда будет выполнять k+1 сравнений. На 64-битной машине это означает наличие максимум 64 итераций цикла while (length > 0). То есть можно написать версию «полностью без ветвления», не имеющую проверки length благодаря намеренно неудачному использованию switch.
size_t length = last - first;
size_t rem;
switch(std::bit_width(length)) {
case 64:
rem = length % 2;
length /= 2;
first += comp(first[length], value) * (length + rem);
case 63:
rem = length % 2;
length /= 2;
first += comp(first[length], value) * (length + rem);
// ...
case 1:
rem = length % 2;
length /= 2;
first += comp(first[length], value) * (length + rem);
}
return first;
Если вам незнаком switch, то можно воспринимать его как переход в код. В нашем случае это конкретное место, с которого мы делаем ровно нужное нам количество сравнений.
«Быстрее ли он?» Нет. Современные процессоры x86 хорошо справляются с условиями циклов, потому что они предсказуемы; крайне вероятно, что программа останется в цикле. И это особенно хорошо, потому что позволяет нам не писать шаблоны или макросы и не копипастить и редактировать код для 64 случаев.
Внимание к производительности
Среднее время исполнения (нс):
std::lower_ |
branchless_lower_ |
asm_lower_ |
sb_lower_ |
sbm_lower_ |
bb_lower_ |
|
|---|---|---|---|---|---|---|
| gcc | 80.68 | 43.65 | 54.92 | 77.22 | 34.19 | 75.64 |
| clang | 78.66 | 90.97 | 51.83 | 80.06 | 83.95 | 74.44 |
| clang -cmov | 61.30 | 43.43 | 54.32 | 33.24 | 35.54 | 32.73 |
Среднее геометрическое время исполнения (нс):
std::lower_ |
branchless_lower_ |
asm_lower_ |
sb_lower_ |
sbm_lower_ |
bb_lower_ |
|
|---|---|---|---|---|---|---|
| gcc | 62.44 | 25.55 | 32.35 | 59.67 | 20.62 | 57.93 |
| clang | 61.24 | 65.72 | 30.67 | 63.59 | 66.91 | 58.19 |
| clang -cmov | 39.17 | 25.14 | 31.21 | 19.81 | 20.91 | 21.33 |
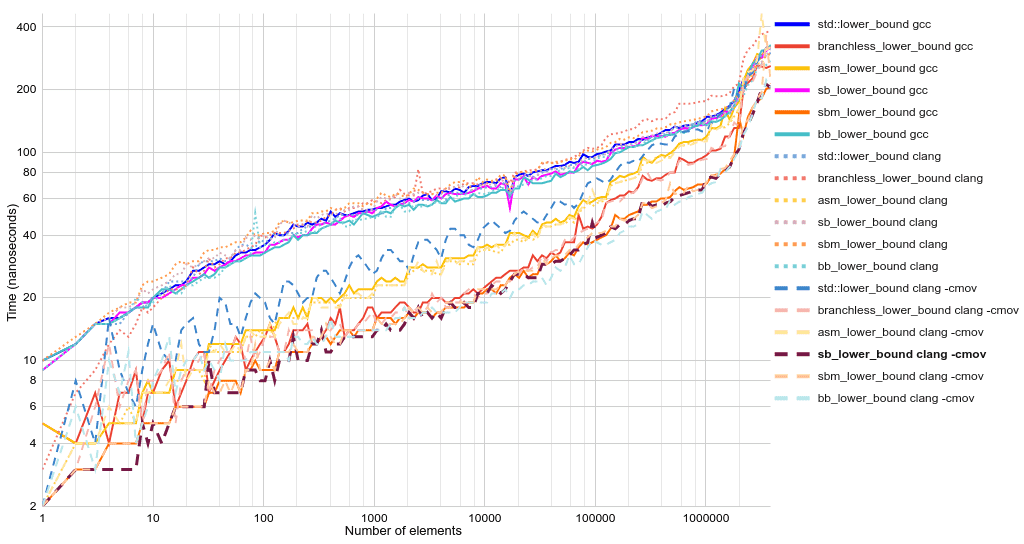
Время исполнения в виде линейных графиков:
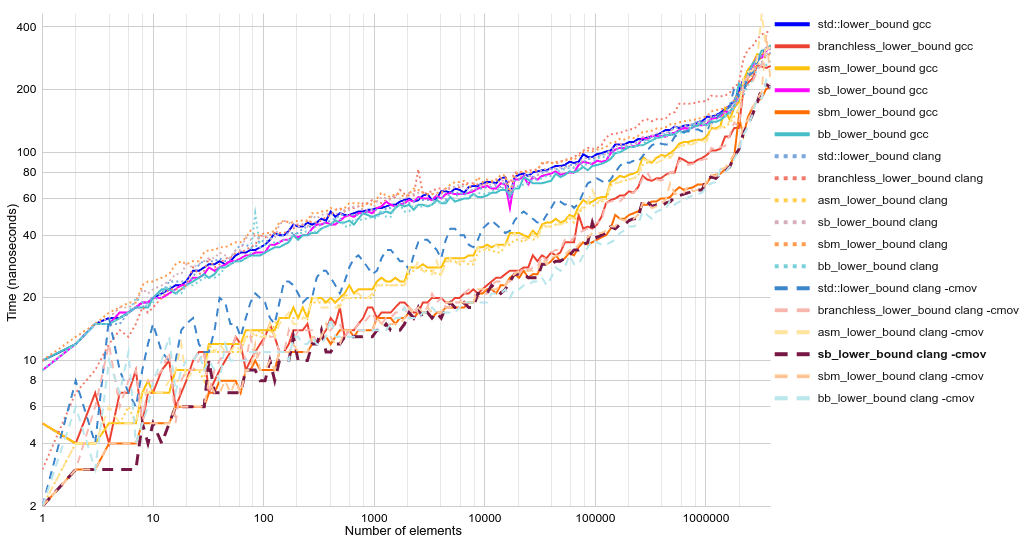
«Что за sbm_lower_bound?» По сути это sb_lower_bound, но изменённый так, чтобы хитростью заставить gcc сгенерировать условную передачу. Разница заключается в замене оператора if на first += comp(first[length], value) * (length + rem). Такой приём следует использовать с предосторожностями и комментариями, потому что в новой версии gcc эта оптимизация может и не работать.
Команды бенчмарков, демонстрирующие опции компилятора:
g++-10 -std=c++20 -Wall -O2 -march=haswell test.cpp -o test && ./test
clang++-10 -std=c++20 -Wall -O2 -march=haswell test.cpp -o test && ./test
clang++-10 -std=c++20 -Wall -O2 -march=haswell -mllvm -x86-cmov-converter=false test.cpp -o test && ./test
-march=native и отсутствие -march несущественно влияют на результаты. Бенчмарки замерялись на intel i7 kaby lake.
▍ Ошибки прогнозирования ветвлений
Изучить ошибки прогнозирования/промахи ветвления можно при помощи perf:
# clang
perf stat ./test
# [..]
16,599.95 msec task-clock:u # Использована 1000 CPU
# [..]
30,309,755,516 instructions:u # 0.53 команды на такт
6,941,783,502 branches:u # 418.181 М/с
1,203,569,540 branch-misses:u # 17.34% от всех ветвлений
# clang -cmov
perf stat ./test
# [..]
10,982.97 msec task-clock:u # Использована 1000 CPU
# [..]
32,603,123,521 instructions:u # 0.90 команды на такт
4,070,883,093 branches:u # 370.654 М/с
35,954,999 branch-misses:u # 0.88% от всех ветвлений
-cmov устраняет примерно 2,9 миллиарда ветвлений и примерно 1,2 миллиарда промахов ветвлений, то есть устраняет ошибочно спрогнозированные в 41% случаев ветви. Это близко к 50%, которых бы мы ожидали при полностью непредсказуемом ветвлении, при совершенной случайности и бенчмарках. В таком случае -cmov привёл бы ещё к более высоким показателям улучшений.
▍ Производительность при более медленной comp()
В качестве реалистичных сценариев двоичного поиска с более медленной функцией comp() можно взять поиск идентификаторов, телефонных номеров, аккаунтов и ключевых слов. Поэтому я остановился на тестировании 8-байтными строками.
Среднее время исполнения (нс):
std::lower_ |
branchless_lower_ |
sb_lower_ |
sbm_lower_ |
bb_lower_ |
|
|---|---|---|---|---|---|
| gcc | 160.01 | 205.24 | 165.66 | 193.96 | 163.91 |
| clang | 157.71 | 178.77 | 162.68 | 166.00 | 157.22 |
| clang -cmov | 156.06 | 193.70 | 164.71 | 181.57 | 157.48 |
В этом случае std::lower_bound очень незначительно, но стабильно быстрее, чем sb_lower_bound. Чтобы всегда обеспечивать наилучшую производительность, библиотеки могут использовать при непосредственной работе с примитивными типами sb_lower_bound, а во всех остальных случаях использовать std::lower_bound.
Ассемблерный код
Оптимизация производительности близкого к железу кода не может считаться завершённой без исследования сгенерированного ассемблерного кода. Впрочем, вы можете спокойно пропустить этот раздел.
Время% | команды
// std::lower_bound, clang -cmov, ассемблерный код самого горячего цикла
1.68 │20: mov %rsi,%rcx // rcx = length
3.20 │ shr %rcx // rcx = length / 2
1.08 │ mov %rcx,%rdx // rdx = length / 2
4.42 │ not %rdx // rdx = binary_not(rdx) = -length / 2 - 1
2.85 │ add %rsi,%rdx // rdx = length - length / 2 - 1
63.41 │ vucomiss (%rax,%rcx,4),%xmm0 // Сравниваем first[rcx] с value, устанавливаем FLAGS
0.21 │ lea 0x4(%rax,%rcx,4),%rsi // rsi = first + length / 2 + 1
10.14 │ cmova %rsi,%rax // first = compare_res ? first : rsi
4.87 │ cmovbe %rcx,%rdx // rdx = not compare_res ? length / 2 : rdx
0.88 │ mov %rdx,%rsi // rsi = rdx (новая длина)
0.33 │ test %rdx,%rdx // Устанавливаем FLAGS на основании rdx
3.90 │ ↑ jg 20 // Переходим к команде 20, если rdx не равно нулю
// sb_lower_bound, clang -cmov, ассемблерный код самого горячего цикла
4.21 │20: shr %rcx // rcx = length / 2
4.70 │ and $0x1,%esi // esi = length % 2
5.00 │ add %rcx,%rsi // rsi = length / 2 + length % 2
68.86 │ vucomiss (%rax,%rcx,4),%xmm0 // Сравниваем first[rcx] с value, устанавливаем FLAGS
0.01 │ lea (%rax,%rsi,4),%rdx // rdx = first + length / 2 + length % 2
11.69 │ cmova %rdx,%rax // first = compare_res ? first : rdx
3.71 │ mov %rcx,%rsi // rsi = length / 2
│ test %rcx,%rcx // Устанавливаем FLAGS на основании rcx
0.02 │ ↑ jne 20 // Переходим к команде 20, если rcx не равно нулю
// branchless_lower_bound, clang -cmov, ассемблерный код самого горячего цикла
3.04 │70: lea (%rdi,%rcx,4),%rax // rax = first + length
71.22 │ vucomiss (%rdi,%rcx,4),%xmm0 // Сравниваем first[rcx] с value, устанавливаем FLAGS
12.26 │ cmova %rax,%rdi // first = compare_res ? first : rax
1.03 │7d: shr %rcx // length /= 2, но также стоит заметить, что здесь устанавливаются FLAGS
1.64 │ ↑ jne 70 // Переходим к команде 20, если length не равно нулю
Ассемблерный код branchless_lower_bound очень короткий и понятный. Хотя это хороший показатель скорости, sb_lower_bound выигрывает в тестах производительности из-за низких дополнительных затрат.
Заключение
Если в самой медленной части вашей программы есть поиск и/или сравнения, которые процессор не сможет спрогнозировать, то попробуйте clang с -mllvm -x86-cmov-converter=false (если вы работаете с процессором x86).
Если вы выиграете от более быстрого двоичного поиска, то попробуйте sb_lower_bound (или для gcc можно также попробовать sbm_lower_bound). Код я сделал опенсорсным с лицензией MIT.
Код вместе с бенчмарками выложен здесь: github.com/mh-dm/sb_lower_bound/.
Если у вас есть какие-то идеи, мысли или дополнения, то можете оставить комментарий здесь.
Дополнение
В комментариях автор orlp.net сообщил, что sb_lower_bound можно немного отрефакторить, чтобы уменьшить количество ассемблерных команд в горячем цикле с 9 до 8.
// sb_lower_bound с рефакторингом
auto length = last - first;
while (length > 0) {
auto half = length / 2;
if (comp(first[half], value)) {
// length - half равно half + length % 2
first += length - half;
}
length = half;
}
return first;
При использовании clang -cmov происходит небольшое ускорение, среднее время исполнения снижается с 33 нс до 32 нс.
▍ Предварительная выборка
Также в комментариях порекомендовали методику ещё большего ускорения при помощи предварительной выборки (prefetching). Предварительная выборка копирует отдельные части памяти в кэш (обычно L1/L2), поэтому когда предварительно переданные данные нужны, то загрузка длится только время задержки кэша L1/L2 (примерно 4/12 тактов), а не время более медленного кэша (L3, примерно 40 тактов) или памяти (примерно 200 тактов). Примеры таймингов. Для этого существует __builtin_prefetch() поддерживаемая и gcc, и clang.
Допустим, мы собираемся выполнить сравнение с элементом по индексу length / 2. Мы можем выполнить предварительную выборку по индексу length / 4 и length * 3 / 4. Или также можем выполнить предварительную выборку с делением length / 8, что даёт 4 дополнительных места в памяти. В случае деления по length / 4 один из каждых двух предварительно переданных элементов будет отброшен, удваивая нагрузку на кэш. Если деление будет length / 8, то впустую будут выброшены пять из каждых предварительно переданных элементов. Также существуют дополнительные затраты на вычисление областей и предварительную выборку, которые будут достаточно большими в горячем цикле, над укорачиванием которого мы так упорно трудились.
Наконец, если мы уже выполнили несколько полных поисков, то изначальные разбиения, скорее всего, уже будут находиться в кэше, потому что в современные кэши L2 размером 256КБ и более может вместиться довольно много элементов.
При проверке различных стратегий предварительных выборок, как мы и ожидали, ни одна не помогла при работе с массивами менее 256 КБ. Вот sb_lower_bound, но с добавленной предварительной выборкой для массивов от 256 КБ:
// sbp_lower_bound
auto length = last - first;
// Размер подобран так, чтобы приблизительно помещаться в кэш L2
constexpr int entries_per_256KB = 256 * 1024 / sizeof(T);
if (length >= entries_per_256KB) {
constexpr int num_per_cache_line = std::max(64 / int(sizeof(T)), 1);
while (length >= 3 * num_per_cache_line) {
auto half = length / 2;
__builtin_prefetch(&first[half / 2]);
// length - half равно half + length % 2
auto first_half1 = first + (length - half);
__builtin_prefetch(&first_half1[half / 2]);
first = comp(first[half], value) ? first_half1 : first;
length = half;
}
}
while (length > 0) {
auto half = length / 2;
auto first_half1 = first + (length - half);
first = comp(first[half], value) ? first_half1 : first;
length = half;
}
return first;При тестировании, аналогичном приведённому ранее, для размеров в интервале до примерно 4 миллионов записей (или 16 МБ) средняя скорость исполнения снижается с 32 нс до 26 нс. Здесь я должен признать, что моя исходная точка останова размеров оказалась слишком маленькой. Так что давайте заберёмся гораздо выше, теперь примерно до 128 миллионов записей (или 512 МБ). Это намного больше, чем L3, но всё равно остаётся достаточно разумным размером набора данных.
Время исполнения в виде линейных графиков:
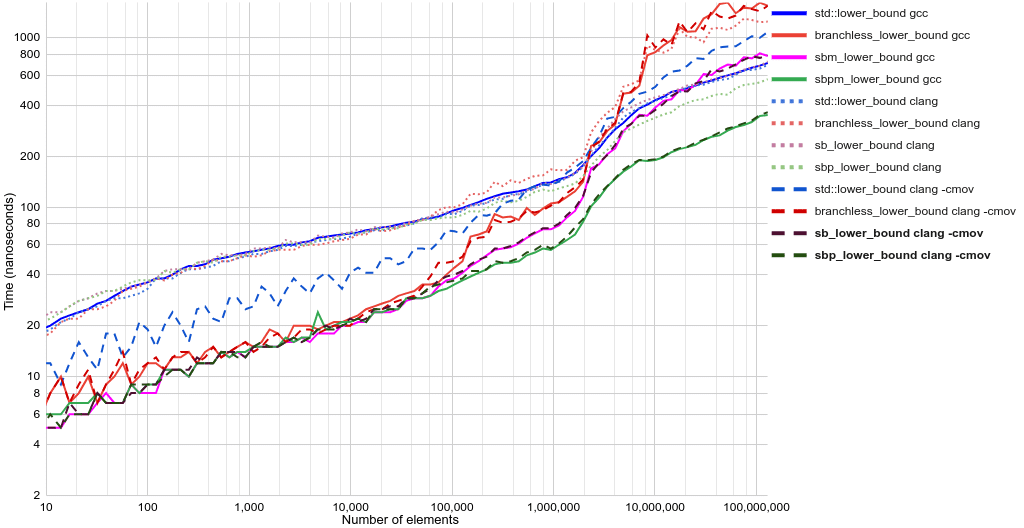
Происходят интересные вещи.
std::lower_boundбез ветвления, которая генерируется при помощиclang -cmov, при огромных размерах массивов медленнее, чем версия с ветвлением. Современные CPU следуют по спрогнозированным ветвлениям, в том числе и выполняют загрузку из памяти (по сути, предварительную выборку), и спекулятивно проводят работу с этими данными (по сути это кошмар для безопасности).sbpm_lower_bound— это версияsbm_lower_boundс предварительной выборкой, которая умножается на boolean, чтобы хитростью заставить gcc генерировать код без ветвления.- При сравнении среднего времени
std::lower_bound(161 нс) и версии с предварительной выборкой (71 нс) мы получаем ускорение примерно в 2,3 раза.
▍ Быстрее?
▍ Вставляемая замена для std::lower_bound
На графике производительности есть всплеск/аномалия в интервале 1-10 миллионов элементов, так что в теории она может быть быстрее. На практике код с предварительной выборкой становится хаотичным и в нём появляются волшебные константы. В процессе написания этого поста у меня была восхитительная (маленькая) возможность внести вклад в gcc/libstdc++ и/или llvm/libc++. Я остановлюсь на этом, потому что вероятность становится ещё меньше с добавлением сложности.
▍ Ломаем ограничения std::lower_bound
В комментариях также упомянули интересный вариант двоичного поиска Эйтцингера, в котором входной массив модифицируется (в двоичную промежуточную «кучу»), чтобы операции поиска были удобны для кэширования. Я мог бы подумать, насколько быстрыми могут быть SIMD-оптимизированные K-ичные деревья, но размышлять об этом не понадобилось: от 7 до 15 раз быстрее, чем std::lower_bound (16-ичного дерева int), как показал Сергей Слотин на CppCon 2022.
Ссылки
- А ВОТ RUST… Rust быстрый, но вы действительно хотели бы, чтобы мой первый пост был посвящён unsafe-коду?
- А ВОТ ZIG… В Zig нет двоичного поиска наподобие
lower_bound(), только вот это. - Всегда есть подходящий XKCD.
- При помощи clang мы можем выполнить
__builtin_unpredictable(comp(first[half], value)), но это ничего не даёт (протестировано на v10-13). - У gcc есть
__builtin_expect_with_probability(cond, 0, 0.5), но это ничего не даёт (протестировано на v10).
Автор:
ru_vds






