
Есть несколько причин смотреть на игры как на нечто большее, чем просто на развлечения. Как станет яснее по ходу дела, многие игры основаны на сложных вычислительных задачах, хотя зачастую и с более низким «входным барьером», поскольку они редко требуют наличия формального образования.
Многие игры и головоломки интересны своей сложностью, и для их решения требуется определённая смекалка и некоторые навыки. Почти всегда трудность решений можно показать математически в виде результатов вычислительной разрешимости. К примеру, каждая NP-полная задача в некотором смысле является головоломкой, и, наоборот, многие головоломки являются NP-полными. Игры для двух игроков часто имеют более высокую сложность, например, PSPACE. На Хабре есть достаточно подробное руководство по сложным вычислительным задачам.
Некоторые исследователи пренебрежительно относятся к такого рода результатам, считая, что они мало что говорят о трудностях расчета оптимальных стратегий, и описывая NP-трудные игровые позиции как «вырожденные». Но на самом деле NP-полнота — далеко не конец, а начало изучения игры. Она показывает, что игра достаточно сложна, чтобы можно было кодировать в ней интересные вычислительные задачи. Если игра находится в P, она становится тривиальной, как только станет известна характерная особенность идеальной игры, а результаты сложности подразумевают, что такому трюку не нужно учиться.
Конечно, NP-полнота или даже PSPACE-полнота не исключает возможности точного вычисления алгоритма игры, правда, для наихудшего случая могут потребоваться экспоненциальные алгоритмы, которые интересно разрабатывать, анализировать и реализовывать.
Существует любопытная связь между вычислительной сложностью и качеством головоломки. Лучшие головоломки являются как минимум NP-полными (хотя некоторые неплохие головоломки можно обнаружить и в P, полагаясь на пробелы человеческой интуиции, а не на их вычислительную сложность).
Некоторые головоломки сложнее, чем NP (например, сокобан является PSPACE-полной), но это всего лишь означает только то, что задача может обладать раздражающе длинной последовательностью манипуляций при её решении. В играх для двух игроков можно встретить подобное явление на ещё более высоком уровне сложности. Дерево потенциальных взаимодействий в игре обычно приводит к таким результатам PSPACE-полноты, которые более интересны, чем PSPACE-полнота головоломок для одного игрока.
Существуют игры ещё сложнее — EXPTIME-полные (например, го). В таких играх может потребоваться утомительно длинная последовательность ходов. Возможно, некоторые игры или головоломки, в которых игроки начинают с неполным знанием игры или конфигурации головоломки, могут привести к другим типам полноты (например, MA-полнота или #P-полнота) для нахождения идеального начального хода.
В этой статье мы в первую очередь рассмотрим некоторые настоящие игры и головоломки, то есть игры, придуманные для того, чтобы в них играли, а не для того, чтобы их анализировали. Так или иначе, сразу предупреждаю, во-первых, в одной статье невозможно описать все игры, да и просто перечислить та ещё задача, а во-вторых, понятие NP-полноты или другой сложности игры — это не то понятие, которое можно было бы применить к одной головоломке или игровой позиции или даже к конечному набору позиций. Имеет смысл говорить только о бесконечном семействе задач как о NP-полных. По этой причине такие игры, как шахматы, сами по себе не могут быть NP-полными, поскольку имеют конечное число возможных позиций. Однако во многих случаях имеет место естественное обобщение некоторой конечной игры или головоломки на бесконечное семейство игровых позиций на сколь угодно больших игровых полях, в которых имеет смысл говорить о NP-полноте. Тот факт, что эти бесконечные обобщения сложны в вычислительном отношении, даёт нам некоторое основание полагать, что исходные конечные игры также сложны в каком-то менее чётко определенном смысле.
В простых играх из P (например, Nim), как я уже писал выше, существует определённая хитрость, позволяющая найти оптимальный ход при любом состоянии игры, которая заключается в простом выполнении XOR над различными стеками. Игрок может форсировать победу, завершив ход, пока состояние стеков XOR равно 0. Существует несколько различных алгоритмов, которые были довольно детально изучены ранее и никому не составит труда найти эти алгоритмы самостоятельно (например, здесь).
С другой стороны, го и шахматы, очень сложные игры, в которых нет простого алгоритма победы (разумеется, при сравнительно одинаковом уровне подготовки игроков). Сложность игр является одной из причин разницы в популярности и долговечности игр. Шахматы и го интересны и по сей день, даже, несмотря на то, что компьютеры уже превосходят в этих играх всех игроков.
Формальное исследование сложности игры может быть проведено с помощью теории сложности, определяющей, к каким именно классам сложности относятся эти проблемы, и демонстрирующей ранее неизвестные отношения между многими различными играми. Классы сложности устанавливаются в зависимости от того, как сложность (в основном время решения) задачи увеличивается с её размером. Это не всегда относится к играм напрямую, в которые в основном играют на доске фиксированного размера. Хотя в го можно играть на досках разного размера, существует фиксированный стандартный размер. Однако, глядя на игру через призму теории сложности, можно обнаружить, что проблема в некотором смысле всё равно обладает определённой затейливостью в играх для двух игроков, что показывает глубину игры и различные виды подзадач, которые обнаруживаются в процессе игры.
Аналогичный аргумент можно использовать для многих других настольных игр, поскольку каждая последующая конфигурация игрового поля представляет собой новую головоломку. Да, если существует определённая хитрость решения, то независимо от количества игровых состояний всегда есть возможность быстрого выигрыша. В другом случае, если хитрости нет, то, вероятно, обнаружатся особенно интересные варианты, дающие новые головоломки и очень любопытные эндшпили. Итак, перейдём к описанию некоторых игр, в которые ваш покорный слуга имел неосторожность играть.
Амазонки
Признаюсь честно, эта игра была для меня открытием. Она была изобретена шахматным энтузиастом Вальтером Замкаускасом в 1988 году. Амазонки обладают рядом свойств, которые делают их интересными для теоретического изучения. Как и в го, эндшпили естественным образом разделяются на независимые подыгры и изучаются с помощью комбинаторной теории игр. В Амазонках из типовой позиции доступно очень большое количество ходов, даже больше, чем в го на стандартном гобане, что делает простые алгоритмы поиска непрактичными. Классическая игра является PSPACE-полной.
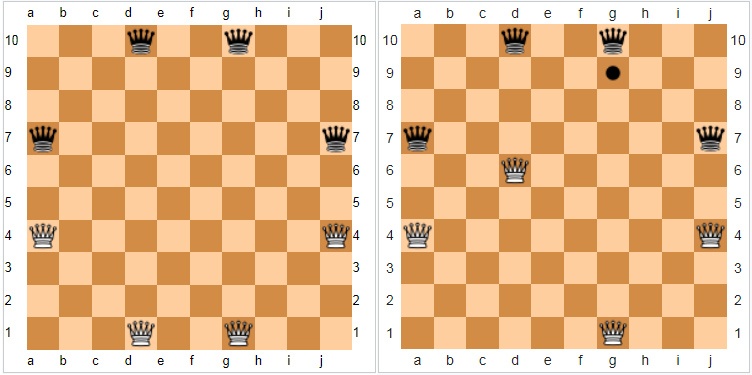
Для игры используется стоклеточная доска. Стандартная начальная позиция и первый ход на рисунке выше. У каждого игрока четыре фигуры, в качестве которых обычно используют шахматных ферзей (с присущей им манерой хода) и набор маркеров для стрел. Белые ходят первыми, а ходы чередуются. На каждом ходу игрок должен сначала переместить амазонку, а затем пустить стрелу этой амазонкой. Стрела движется также как и фигуры. Квадрат, на который попала стрела, блокируется (никакая амазонка или стрела не могут перемещаться по квадрату или пересекать его). Фигуры бессмертны. Первый игрок, который не сможет совершить ход, проигрывает.
Амазонки — игра гибрид, обладающая тактическими свойствами шахмат и захвата территории го. Стратегия игры предполагает ограничение мобильности фигур противника и захват изолированной территории для собственных фигур. Таким образом, изначально игра является PSPACE-полной, а эндшпили, в которых фигуры противоположных цветов отделены друг от друга, являются NP-трудными.
Криптарифмы
На эту игру я залип совершенно случайно в процессе работы над решением небольшой криптологической задачи, и по большей части эта статья обязана своим появлением именно этой игре. Криптарифмы, или буквенные головоломки, представляют собой арифметические формулы, в которых цифры заменены буквами или иногда другими символами. Изобретение криптарифметики приписывают древнему Китаю. Первоначально это искусство было известно как буквенная арифметика или словесная арифметика. Самым распространённым и известным примером такой головоломки является криптарифм, опубликованный Генри Дьюдени в 1924 году в журнале Strand Magazine: SEND+MORE=MONEY (подробное решение).

Существует несколько отличающихся вариантов криптарифм, но главными особенностями этого вида головоломок являются следующие:
— решение криптарифма должно быть единственным, чтобы избежать коллизий,
— слова всегда преобразуются в математическое выражение (будь то классические математические операторы или логические условия),
— цифровая база, если не указано иное 0-9, а числа не должны начинаться с нуля.
В общем, при использовании десятичной системы счисления любой криптарифм является конечной задачей и принадлежит NP. Однако при использовании других систем счисления, является NP-полной. На Хабре имеется довольно любопытная статья, в которой описывается один из возможных алгоритмов генерации криптарифмов.
Точки и квадраты
Пипопипетта, La Pipopipette
В эту, как считается, детскую игру играют на бумаге, начиная с рисования прямоугольной решётки из точек (можно использовать лист в клетку). Обычно два игрока по очереди добавляют одну горизонтальную или вертикальную линию между двумя несоединёнными соседними точками. Игрок, заполнивший четвертую сторону коробки 1×1, получает одно очко и делает ещё один ход. Очко обычно записывается путем размещения отметки, идентифицирующей игрока, в поле. Игра заканчивается, когда больше нельзя поместить линии на заранее размеченном поле. Победителем становится игрок с наибольшим количеством очков. Поле может иметь любой размер сетки.
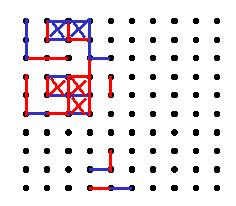
Существует определённый набор выигрышных стратегий игры, однако полной классификации найти не удалось. Большинство игроков играют без всякой стратегии, либо игра делится на две фазы: случайное сегментирование поля и жадное деление добычи. Тем не менее пипопипетта является классическим примером игры, которая сложнее, чем кажется.
В комбинаторной теории игр является беспристрастной игрой, и многие позиции могут быть проанализированы с использованием теоремы Шпрага-Гранди. Однако в этой игре отсутствует обычное правило беспристрастной игры, где побеждает последний игрок, сделавший ход, что значительно усложняет анализ. Обобщённая версия игры, является NP-трудной за счёт сокращения от нахождения множества вершинно-непересекающихся циклов в графах.
Разбираясь с этой игрой, у меня возникли «смутные сомнения», что Эдуард Люка придумал её в процессе создания математической задачи, известной нам под названием «Задача о пушечных ядрах».
Пятнашки
Ещё одна популярная головоломка, правила которой объяснять не нужно. Вкратце классическая игра выглядит как матрица 4×4, в которой плитками с нанесёнными на них цифрами заполнены 15 из 16 позиций и осталось одно незаполненное отверстие. Плитки, примыкающие к отверстию, могут быть перемещены в отверстие, цель состоит в том, чтобы сформировать определённую перестановку плиток (по порядку, магический квадрат и другие). На первый взгляд может показаться, что не о чем тут писать, однако это далеко не так.
Во-первых, в докомпьютерные времена не так уж и много было развлечений, и появление новой головоломки вызывало просто бешеный ажиотаж. Сама история изобретения пятнашек достаточно скандальна и достаточно подробно описана в Вики. Во-вторых, семейство этих головоломок уже десятки лет используется в математике, теории алгоритмов и информатике, и является классической задачей для моделирования эвристических алгоритмов.
Описывать математические свойства этой головоломки подробно не стоит, поскольку об этом достаточно информации. Относительно сложности понятно, что само решение является конечной проблемой, проверка существования решения находится в P, но вот поиск решения с наименьшим количеством ходов является NP-полным. Что интересно «не известен ни один алгоритм, находящий кратчайшее решение для обобщённых пятнашек N×N за разумное время». Если рассматривать эвристические алгоритмы, то «оптимальное решение произвольных конфигураций головоломки 6×6 до сих пор находится за пределами возможностей».
Гекс
Изначально эта игра привлекла моё внимание своей историей. Одним из независимых создателей этой игры является Пит Хейн, а вторым Джон Нэш. Каждый из них был очень необычным человеком.

Правила игры очень просты. Игроки по очереди размещают фигуры на ромбовидной доске, состоящей из шестиугольных плиток. Каждый игрок владеет двумя противоположными сторонами доски, размеченными цветом, и стремится соединить эти стороны непрерывным путём из фигур. Гекс — игра с нулевой суммой.
При идеальном раскладе в игре для всех N: на пустом игровом поле у первого игрока всегда есть выигрышная стратегия на поле N×N. Однако, если рассматривать игровые ситуации, когда различные позиции игрового поля уже заняты фишками различного цвета, задача по определению того, у какого игрока есть выигрышная стратегия в данной игровой ситуации, является PSPACE-полной.
Шашки
Глупо рассчитывать на то, что на Хабре найдётся человек, не знающий правил игры, однако на самом деле существует много разновидностей шашек и некоторые из них сложней, чем другие. Если вкратце, то игроки перемещают фигуры по диагонали вперед на одну клетку за раз по чередующимся клеткам доски N×N, удаляя фигуры других игроков, перепрыгивая через них по диагонали. Цель игры — побить все шашки соперника или лишить их возможности хода.
При условии введения ограничений числа ходов в зависимости от N уровень сложности игры лежит в PSPACE, однако без ввода ограничений шашки относятся к классу EXPTIME-полных задач.
Го
В этой древней настольной игре участвуют два игрока, один из которых играет чёрными, а другой — белыми. Они по очереди кладут камни на свободные места квадратной деревянной доски (гобан) с целью захвата территории. У игроков в го множество вероятных ходов, что делает эту игру одной из самых сложных игр в мире. Даже если сыграть миллион партий, невозможно сыграть одну и ту же игру дважды. Безграничные возможности го приводят к тому, что игроки могут посвятить игре хоть всю свою жизнь, но при этом так и продолжать познавать её стратегические тонкости.
Го была изобретена в Китае более 2500 лет назад, и считается, что она была завезена в Японию в седьмом веке. Сначала она стала фаворитом при императорском дворе, а затем и у широкой публики, прежде чем была изменена и формализована в игру, которую мы знаем сегодня.
Создание государственных школ этой игры в XVII веке поставило Японию в центр мира го, и с тех пор игра пропитала суть этой страны. Чтобы оценить уровень влияния го на японскую культуру, приведу несколько любопытных фактов.
Лауреат Нобелевской премии, писатель Ясунари Кавабата написал об этой игре в своём magnum opus «Мэйдзин». Интересная серия манги «Хикару и го» способствовала популяризации игры во всем мире, хотя её создатели даже не преследовали такой цели. А в 1996 году японский космонавт Коити Ваката играл в го в космосе с американским космонавтом Дэниэлом Барри. Вообще, идея того, что го является искусством и значительной частью национальной культуры, весьма сильна в Японии.
В марте 2016 года 18-кратный чемпион мира по го Ли Седоль сыграл матч против AlphaGo, и ко всеобщему удивлению проиграл со счетом 4:1. Программа применила ряд новаторских ходов, противоречащих многовековой мудрости го. Хотя эксперты предсказывали, что пройдёт ещё как минимум 10 лет, прежде чем машина сможет обыграть игрока такого уровня, как Ли. Этот результат потряс мир го, многие были просто ошеломлены. Сейчас никто не сомневается, что искусственный интеллект может победить человека в такую игру. Машины могут анализировать и оценивать действия игроков с недоступной для человеческого разума точностью и скоростью, и поэтому профессиональные игроки в го внесли коррективы в свои планы обучения, что сделало его более эффективным.
Математически го является конечной игрой, однако даже без «ко» (специальные правила, связанные с повторением позиций) игра является PSPACE-сложной. С «ко» по японским правилам игра принадлежит множеству EXPTIME-полных. По-видимому, остаётся открытым вопрос о том, является ли го EXPTIME-полной по китайским или американским правилам, однако даже некоторые «простые» эндшпили, в которых доска го разбита на множество небольших независимых областей игры, относятся к PSPACE.
Шахматы
В конце статьи я не мог не упомянуть мои любимые шахматы. Это поистине великая игра. С точки зрения современного уровня развития нейронных сетей и суперкомпьютеров классическая игра уже, кажется, не представляет такой сложности, и по рейтингу Эло машины с лихвой перегнали человека. Однако пока у каждого любителя этой игры в спальне не будет стоять машина с нейросетью на борту, люди будут продолжать играть в эту игру. Да и потом обязательно найдутся любители сразиться.
Конечно, было бы несусветной глупостью описывать подробно правила этой игры, она слишком сложна и хорошо известна. Основная идея состоит в том, чтобы перемещать фигуры по доске 8×8, захватывая фигуры противника, пока игра не закончится матом (игрок выигрывает, форсируя взятие короля противника) или с помощью различных видов ничьих.
В общем, классические шахматы являются игрой с конечным числом возможных позиций (поэтому, собственно, машины опередили человека), однако расширение доски до сколь угодно большого игрового поля типа N×N также переводит игру в класс EXPTIME.
P.S. Как вы могли заметить, в топике в основном описываются игры для нескольких игроков, за исключением криптарифм и пятнашек. Однако дело в том, что в эти игры в моей семье тоже принято играть вдвоём, поэтому после проработки материала решил их не убирать.
«Почему нет кубика Рубика», — спросите вы. Ответ я дам такой — «42» шутка. На самом деле, кубик Рубика — культурно-математический феномен. Существует отдельное направление математики, изучающее алгоритмы сборки и оценки их работы, соревнования по сборке и многое другое. Так что глупо было бы даже упоминать его.
По каждой из игр, фигурирующих в топике, можно было бы написать отдельную статью как минимум, но я, пожалуй, ограничусь материалами и приложениями.
— Hex is PSPACE-complete (PDF)
— Amazons is PSPACE-complete (PDF)
— 150 puzzles in crypt-arithmetic (PDF)
— Небольшое описание вариантов Hex (PDF)
Продолжение следует...
НЛО прилетело и оставило здесь промокод для читателей нашего блога:
— 15% на все тарифы VDS (кроме тарифа Прогрев) — HABRFIRSTVDS
Автор: Александр






