Здравствуйте, меня зовут Николай Стрекопытов и я придумал как подбирать гиперпараметры бескомпромиссно лучше GridSearch’а. Нужно лишь изменить порядок вычислений. И да, это заявка на обновление индустриального стандарта - скоро вы сможете улучшить свои ML-пайплайны заменой нескольких строчек кода.

Сначала коротко
Разберем как проводит вычисления GridSearch, а как ProgressiveGridSearch. Первый перебирает все возможные комбинации стандартным вложенным циклом, то есть если нужно перебрать элементы матрицы, то первый алгоритм сначала переберет все столбцы по первой строке и только после приступит ко второй строке, то есть это просто брутфорс. Я предлагаю действовать разумнее. Постепенно увеличивать разрешение вычислений, то есть сначала получить представление о функции крупным мазками по всему диапазону, затем средними мазками, а дальше мелкими и так далее до останова (такой подход дает возможность адекватно приближать функцию в невычисленных узлах).
В качестве функций возьмем два изображения, визуально процессы выглядят так:
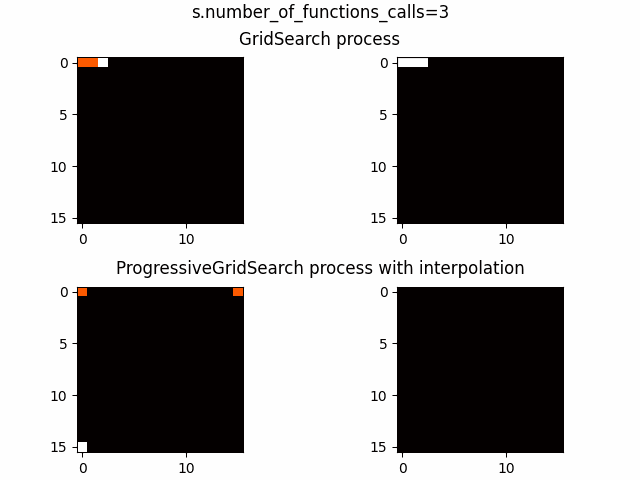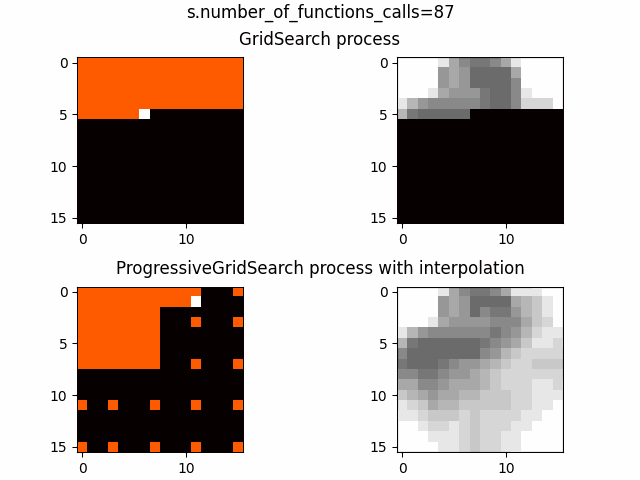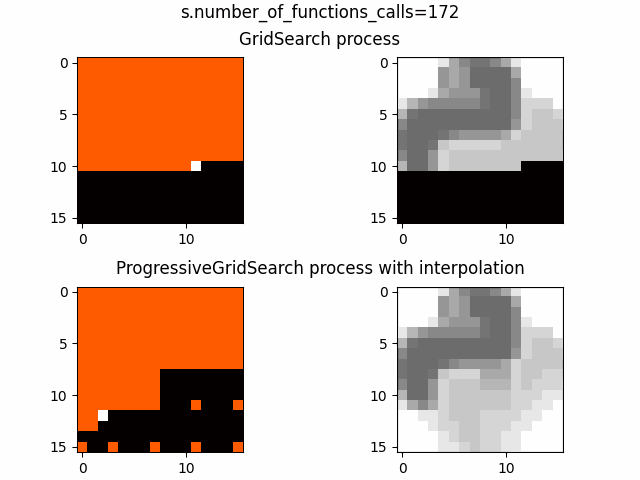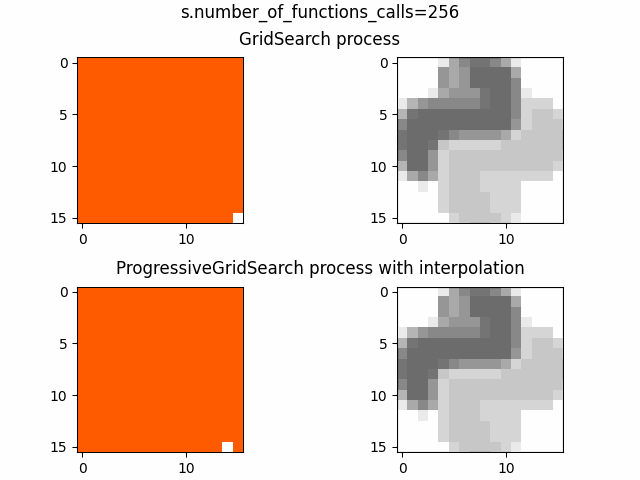

Пока не ясно лучше ли метод, чем аналоги из optuna, но его уже можно использовать как генеративный алгоритм для фильмов ужасов (гифку получше залью чуть позже)
По анимациям процессов видно, что пока GridSearch проходит одну строчку ProgressiveGridSearch уже получает массу информации о ландшафте функции и это для размерности 2 и порядка разрешения 4 и отрыв растет прямо пропорционально размерности и порядку разрешения, что видно по второй анимации, где размерность все те же 2, но порядок разрешения уже 7
Теперь подробнее
Решение получилось красивым, а, как известно, математические результаты бывают либо красивыми, либо неправильными.
Сразу предупрежу, что речь дальше пойдет о многокритериальной оптимизации, гиперкубах и рекурсии, которые в совокупности порождают фрактал поэтому текст под спойлером предназначен для смелых духом и полных сил, а остальные могут поддержать меня поставив статье плюсик и звездочку репозиторию, посмотреть картинки и перейти к заключению.
Математическая сторона
Идея строится на том чтобы получать представление о ландшафте функции сначала крупными мазками, затем средними, затем мелким и так далее до заданной мелкости или пока не сработает критерий останова. Такой подход дает инвариантность относительно стартовой точки поиска, а это уже огромное преимущество
Математически задачу можно поставить так: следующий узел-кандидат выбирается так, что он дальше всего расположен от всех предыдущих узлов. Первыми узлами будет разумно выбрать вершины гиперкуба (отрезка/квадрата/куба для 1D/2D/3D), являющимся нашим диапазоном вариантов, что эквивалентно формуле:
Решение этой многокритериальной оптимизационной задачи оказалось неожиданно красивым и легко вычисляемым, рассмотрим его для одномерного случая
В качестве я взял квадрат евклидовой нормы и точки-решения оказались серединами отрезков, границы которых уже в последовательности, но внутри отрезка нет ни одной точки последовательности
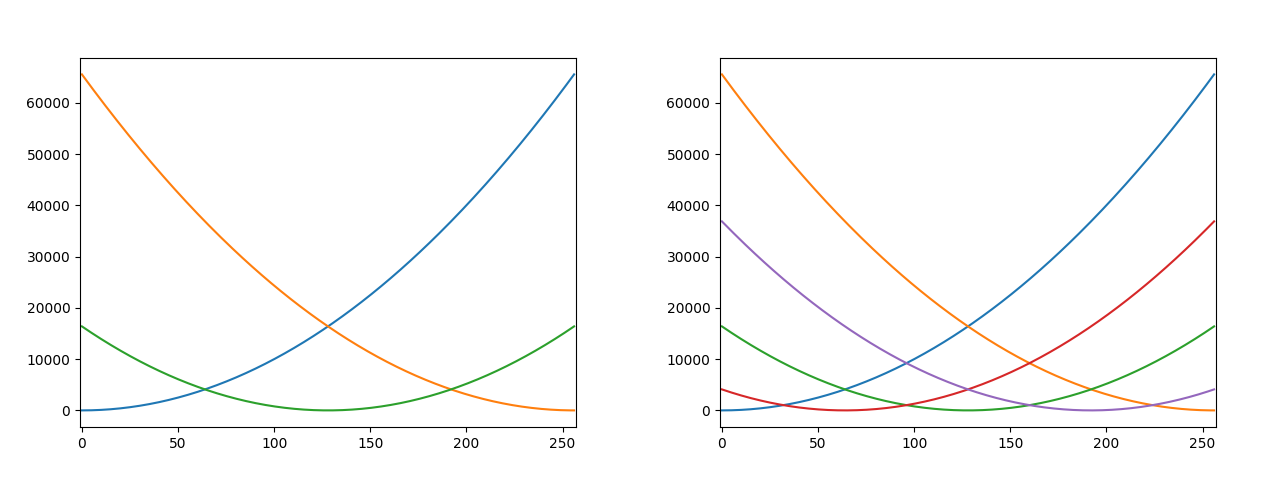
По графикам видно, что эти точки действительно являются Парето-оптимальными (при изменении координат нельзя увеличить ни один из функционалов не уменьшив хотя бы один, это вариант обобщения понятия экстремума для многомерных критериев)
Для большей наглядности рассмотрим порядок без построения кривых расстояний
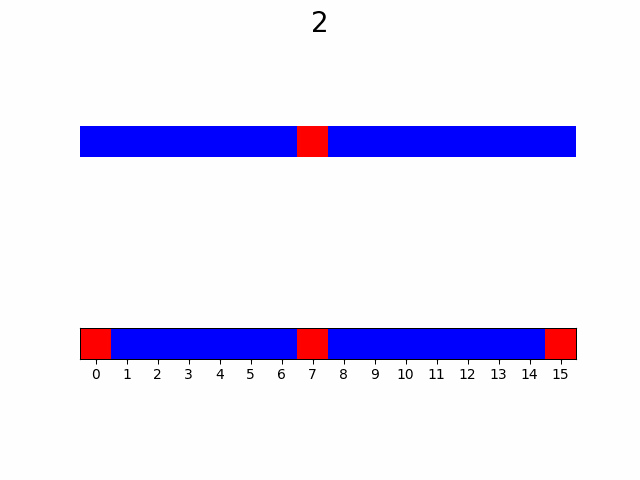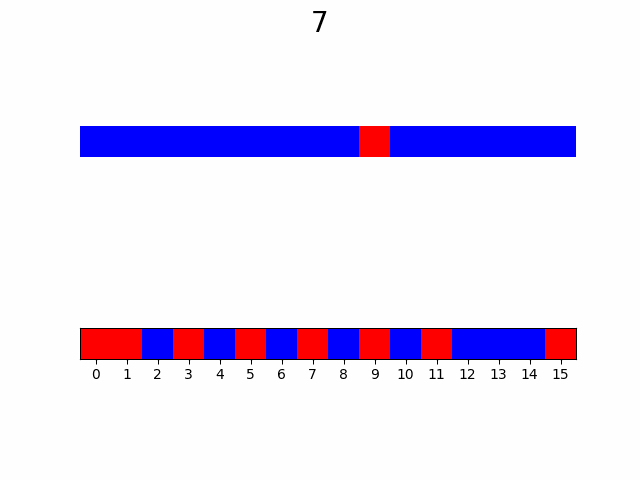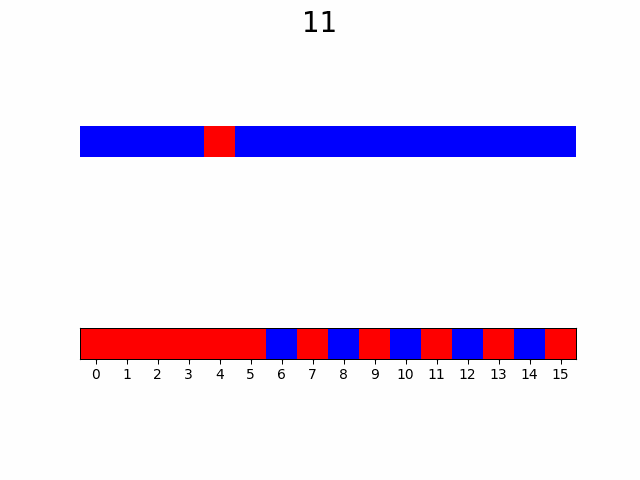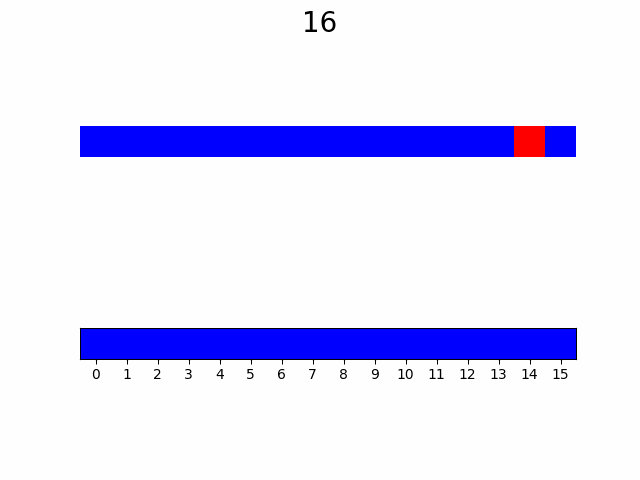
Но как этот результат обобщается для N-мерного случая? Здесь и появляются гиперкубы и фрактал. Точками-решениями будут являться вершины гиперкуба, а каждый гиперкуб делится на с вдвое меньшей стороной. Таким образом возникает последовательность вложенных друг в друга гиперкубов, образующая фрактал, вершины которых являются решением задачи оптимального упорядочивания
При желании эту закономерность можно увидеть и в одномерном случае, но на двумерном уже сильно заметнее

Поскольку речь идет о поиске на сетке, то я свожу этот метод к целочисленному, а не непрерывному, а это дает свой вклад: 1) это универсализирует метод потому что мы вместо точек просто оперируем индексами и автоматом получаем и целочисленный, и непрерывный метод, да еще и с кастомизируемыми по распределению шага сетками 2) Парето-оптимальных решений у целочисленной задачи больше потому что максимально далекое вещественное число от 0 и 15 внутри отрезка это 7.5, а самых далеких целых уже два - 7 и 8 и эту особенность нужно учитывать, иначе будут коллизии и повторные вычисления
Приступаем к программированию
Оказалось, что алгоритм оптимального упорядочивания узлов по сути является построением dim-арного дерева заданной глубины и обход его узлов поэтажно.
Нам нужно всего два класса - Hypercube и ProgressiveGridSearch
import numpy as np
from typing import Callable, List, Union
# Это просто "контейнер" для узлов-кандидатов, который еще и дает потомков
# лежащих внутри него гиперкубов и тоже являющихся "контейнерами" для узлов-кандидатов
class Hypercube:
def __init__(self, resolution_degree: int, start_point: np.array, parent=None):
self.resolution_degree = resolution_degree
self.start_indexes = start_point
self.parent = parent
self.side = 2 ** resolution_degree - 1
self.dim = self.start_indexes.shape[0]
self.node_order_graph = None
self.set_node_order_graph()
def set_node_order_graph(self):
self.node_order_graph = []
schema_string = '{0:0' + str(self.dim) + 'b}'
for node_number in range(2 ** self.dim):
binary_mask = schema_string.format(node_number)
point = np.array(self.start_indexes)
for index, flag in enumerate(binary_mask):
if flag == '1':
point[index] += self.side
self.node_order_graph.append(point)
def split(self):
for node in self.node_order_graph:
yield Hypercube(resolution_degree=self.resolution_degree - 1,
start_point=np.around((node + self.start_indexes) / 2).astype(int),
parent=self)
def compute_curr_depth(self):
res = 0
if self.parent is None:
return res
else:
parent = self.parent
while parent is not None:
res += 1
parent = parent.parent
return res
class ProgressiveGridSearch:
def __init__(self, func: Callable, params: List, stop_criterion: Callable, max_resolution_degree: int = 10):
self.func = func
self.params = params
self.stop_criterion = stop_criterion
self.max_resolution_degree = max_resolution_degree
self.number_of_nodes = 2 ** max_resolution_degree
self.dim = 0
self.grids = []
for param in self.params:
if type(param) is Real:
self.dim += 1
grid = np.linspace(param.left_boundary, param.right_boundary, num=self.number_of_nodes)
self.grids.append(grid)
elif type(param) is Integer:
self.dim += 1
grid = np.arange(param.left_boundary, param.right_boundary)
self.grids.append(grid)
self.mask = np.zeros([self.number_of_nodes] * self.dim).astype(bool)
self.values = np.full_like(self.mask, fill_value=np.nan).astype(float)
self.nodes_queue = None
self.curr_hypercube = None
self.number_of_functions_calls = None
def __iter__(self):
hypercube = Hypercube(resolution_degree=self.max_resolution_degree, start_point=np.zeros(self.dim).astype(int))
self.generator = (curr_hc.node_order_graph for curr_hc in self.append_generator(hypercube))
self.number_of_functions_calls = 0
self.nodes_queue = iter([])
return self
def __next__(self):
try:
node_indexes = next(self.nodes_queue)
# Это фильтрация коллизий
if self.mask[tuple(node_indexes)].item() is True:
return next(self)
node_point = []
for k, index in enumerate(node_indexes):
node_point.append(self.grids[k][index])
node_point = np.array(node_point)
# Это префильтрация коллизий
if self.curr_hypercube.resolution_degree != self.max_resolution_degree and self.curr_hypercube.resolution_degree != 1:
if np.any(node_indexes % 2 == 0) and np.sum(node_indexes) % 2 == 0 and np.sum(node_point) != 0:
return next(self)
b = node_indexes - self.curr_hypercube.start_indexes
if np.any(b % 2 == 0) and np.all(node_indexes != 0):
return next(self)
self.mask[tuple(node_indexes)] = True
self.number_of_functions_calls += 1
return node_point, node_indexes
except StopIteration:
self.nodes_queue = iter(next(self.generator))
return next(self)
def append_generator(self, hypercube: Hypercube):
lst = [hypercube]
while lst:
self.curr_hypercube = lst.pop(0)
yield self.curr_hypercube
if self.curr_hypercube.resolution_degree == 1:
continue
for sub_elem in self.curr_hypercube.split():
lst.append(sub_elem)
# Здесь будет расположен сам цикл поиска минимума/максимума функции на сетке с критериями останова
def optimize(self):
for point in self:
raise NotImplementedError
optimizer = ProgressiveGridSearch(func=evaluator,
params=[Real('lr', left_boundary=1e-10, right_boundary=1e-1),
Integer('batch_size', left_boundary=16, right_boundary=512),
Integer('latent_space_dimension', left_boundary=128, right_boundary=1024),
String('activation', necessary_values=['relu', 'hard_sigmoid'])],
stop_criterion=LastDifferenceBetweenBestLowerThan(1e-1)))Более ста строк чтобы превзойти вложенный цикл
Заключение
Преимущества алгоритма:
-
В основном пользователи GridSearch не знают хорошего шага сетки, по которой задают поиск и задают его интуитивно. Но они с большим шансом знают желаемое время на поиск и желаемую точность, что можно обеспечить сеткой переменного разрешения реализованной в ProgressiveGridSearch
-
Алгоритм легко модифицируется кастомными критериями останова и в будущем фильтрацией узлов на очереди к вычислению (узлов-кандидатов)
-
ProgressiveGridSearch быстрее находит точки близкие к оптимальным (в среднем), то есть просто лучше как метод оптимизации
-
Поиск настраивается проще, нет необходимости указывать шаг сетки, хотя как опция это возможно
-
Преимущество ProgressiveGridSearch над GridSearch стремительно нарастает прямо пропорционально количеству переменных и количеству узлов, которые нужно проверить
Недостатки:
-
Временная сырость продукта - код можно оптимизировать и отсутствует заточенность интерфейса на неизвестные мне, но возможно распространенные, use case'ы из-за недостатка обратной связи - надеюсь на вашу помощь с этим
-
Микроскопический оверхед на вычисления на усреднения узлов, устраняющийся C-extesion’ом и кэшированием порядка узлов для заданных N - размерности и D - вектора разрешений для соответствующих компонент
Планируемые фичи:
-
Кастомные критерии останова
-
Сетка с неравномерным шагом
-
Отдельность повышения разрешения по критерию для каждой переменной
-
Фильтрация узлов-родителей по значению функции в них (например, оставлять лишь половину лучших)
-
Сортировка узлов-кандидатов по аналогичным образом
-
Кэширование порядка узлов?
-
Другие методы оптимизации алгоритмически заданных функция (есть еще несколько оригинальных идей)
-
Оставляйте в комментариях свои мысли, в том числе предлагайте фичи
-
Приглашаю вас в свой блог https://t.me/research_and_deep_learning . В нем я пишу в основном о своих исследования и разработках, но бывают и трезвые оценки и разборы другие работ. В комментариях вы можете повлиять на мои работы до их публикации или просто размылить свои глаза от LLM/GPT нехайповым, но содержательным материалом
-
Пользуйтесь этим продуктом https://github.com/nstrek/progressive_search, расскажите о нем коллегам
-
Если вы нанимаете исследователей или R&D специалистов или вашему проекту нужен свежий взгляд, то с радостью с вами познакомлюсь - я как раз ищу работу
-
Буду рад вашей поддержке в конкурсе статей по ML. Ставьте плюсики статье, я старался и мне сейчас пригодятся эти призы, да и это действительно ценный результат для всей ML-индустрии, хоть и совсем небольшой
Кто увидел возможность оптимизировать оптимизатор им же самим - молодец, а остальные могут дождаться следующей статьи.
Такие вот фракталы и незаметная теория управления на службе у машинного обучения.
ПМ-ПУ лучший и вне СПбГУ
%%% Пока вы видите этот абзац статья и код активно дорабатываются, смело пишите ваши замечания в комментарии или в тг %%%
Над чем я уже точно работаю
-
Доведение кода от прототипа до production-ready
-
Еще более разумный порядок узлов за счет изменения порядка нод-гиперкубов внутри одного этажа
-
Загрузка в PyPI
-
Документация и readme.md
-
Сейчас коллизии фильтруются проверкой, я хочу сделать так чтобы повторные ноды вообще не генерились
-
Картинка, которая более понятно визуализирует фрактал
Кому не хватило красивой картинки с фракталом
Это получилось при разработке в качестве ошибки, экспериментировал с фильтрацией узлов-кандидатов
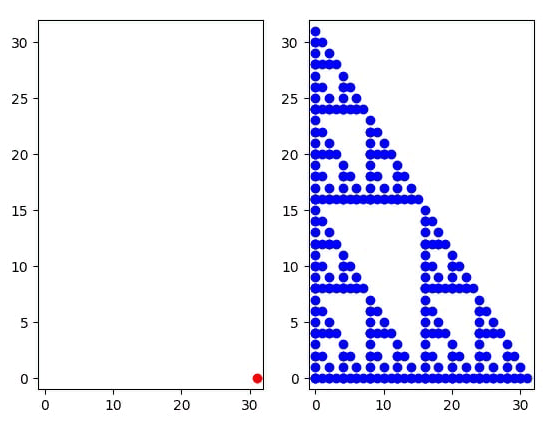
А это по сути https://ru.wikipedia.org/wiki/Треугольник_Серпинского , только у него треугольники равносторонние, а тут прямоугольные
А так выглядит одно из состояний процесса если узлы с последнего этажа случайно перемешать
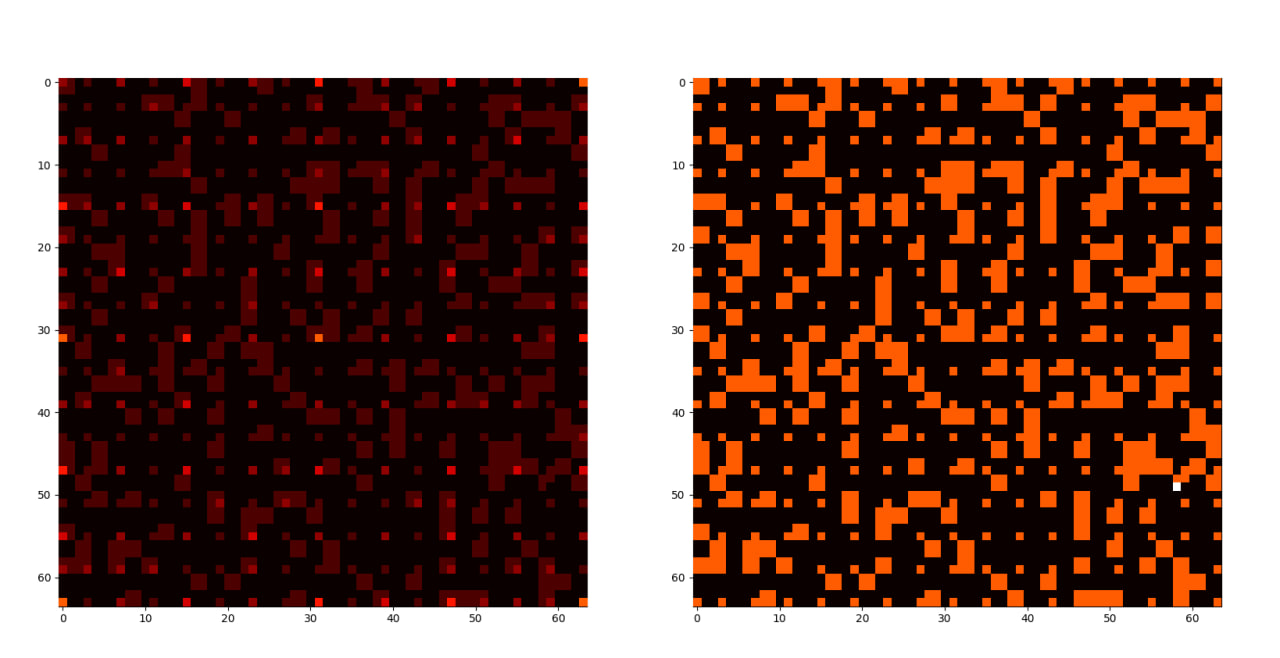
F.A.Q.
Тут пока пусто
Поддержите меня поднятием рейтинга статье, поделитесь статьей с коллегами.
Автор:
nstrek





