Самая маленькая хеш-таблица в мире

1 декабря я в очередной раз поучаствовал в Advent of Code, написав программу на Rust. Если интересно — код можно найти на GitHub. Тут мне хотелось бы рассказать о моём решении задачи, предлагавшейся во 2 день мероприятия, так как это решение, с одной стороны, сверх всякой меры оптимизировано, а с другой — демонстрирует кое-какие полезные приёмы. Чтобы не усложнять себе жизнь — мы рассмотрим лишь первую часть задачи, но те же приёмы можно применить и к её второй части.

Мы начнём входить в курс дела не спеша, но я предлагаю вам не отклоняться от заданного мной курса, так как, после того, как вы полностью прочтёте этот материал, у вас должно появиться понимание того, что именно делает следующая функция, как она работает, как такую функцию написать, и того, почему это — самая маленькая в мире хеш-таблица:

pub fn phf_shift(x: u32) -> u8 {
    let shift = x.wrapping_mul(0xa463293e) >> 27;
    ((0x824a1847u32 >> shift) & 0b11111) as u8
}

Задача

Мы получаем файл, в каждой строке которого содержится символ A, B или C, за которым следует пробел, а потом идёт символ X, Y или Z. Это всё интерпретируется как ходы в игре «Камень, ножницы, бумага».

A = X = Камень
B = Y = Ножницы
C = Z = Бумага

Первая буква (A/B/C) указывает на выбор, сделанный во время хода вашим оппонентом, а вторая (X/Y/Z) — на выбор, который сделали вы. Получив эти данные, мы вычисляем очки, заработанные нами в игре. Очки каждого хода состоят из двух компонентов:

1. Если мы выбрали Камень — мы получаем 1 очко. Бумага даёт 2 очка. Ножницы — 3 очка.

2. Если мы проиграли — получаем 0 очков. Если вышла ничья — 3 очка. Победа даёт 6 очков.

Предположим, имеются такие входные данные, описывающие игру:

A Y
B X
C Z

Расчёт наших очков — результатов этой игры — будет таким:

(2 + 6) + (1 + 0) + (3 + 3) = 15.

Изящное решение

В нормальном решении этой задачи будет проверяться то, имеют ли строки входных данных формат [ABC] [XYZ], а уже потом из строк будут извлекаться две буквы. После преобразования букв в целые числа, 0, 1 или 2, проводимого путём вычитания из их ASCII-кодов кода, соответственно, буквы A или X, сразу же можно посчитать первый компонент наших очков, находимый по формуле 1 + ours. Здесь и далее ours — это очки за выбор игрока, а theirs — очки за выбор противника.

Второй компонент найти немного сложнее, но и его можно красиво рассчитать, используя операции модульной арифметики. Обратите внимание на то, что если Камень = 0, Бумага = 1 а Ножницы = 2, то всегда оказывается, что выбранный вариант, описываемый формулой k + 1 mod 3, одерживает победу над вариантом k. И, аналогично, вариант k выигрывает у варианта k − 1 mod 3. Вот как это можно представить в виде схемы.

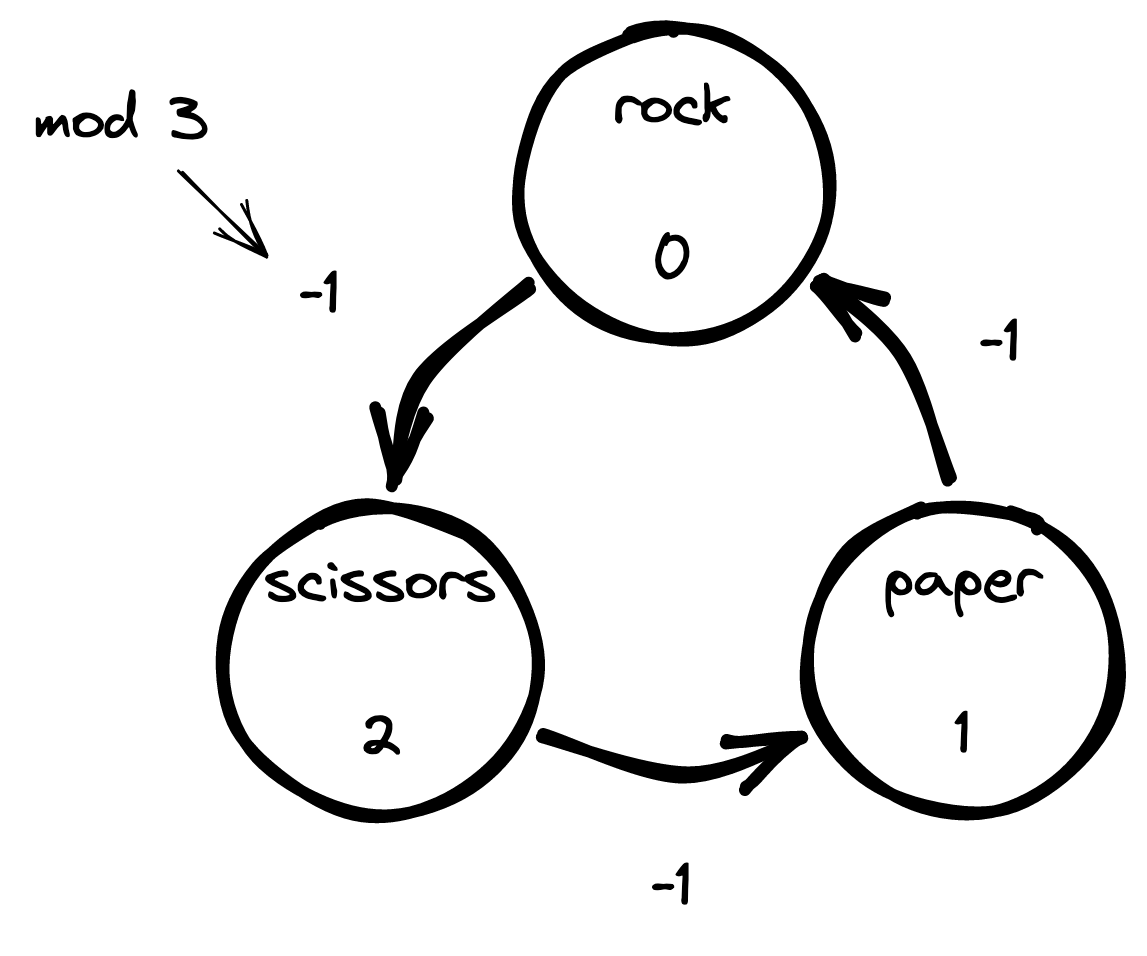
Если поделить на три количество очков, которое в Advent of Code ожидается получить за проигрыш, ничью и выигрыш, то получится, что проигрыш даст 0 очков, ничья — 1 очко, а выигрыш — 2 очка. Эти наблюдения позволяют нам вывести следующее модульное равенство:

1 + ours − theirs ≡ points (mod 3).

Для того чтобы подтвердить правильность этого выражения — обратите внимание на то, что если будет ничья, то ours — theirs даст 0 и нам, как и ожидается, будет начислено 1 очко. Если к ours добавить 1, то от ничьей мы перейдём к выигрышу, и показатель points окажется, как нам и нужно, соответствующим 2. В случае с показателем theirs наблюдается симметричная ситуация. Если добавить 1 к theirs, то мы переходим от ничьей к проигрышу, а point, снова ведя себя так, как нам нужно, оказывается равно 0.

Если представить эти рассуждения в виде кода — получится, что наши итоговые очки рассчитываются так:

1 + ours + 3 * ((1 + ours + (3 - theirs)) % 3)

Обратите внимание на то, что вместо вычисления выражения ours — theirs мы вычисляем выражение ours + (3 — theirs). Делается это из-за того, что в Rust операция взятия остатка от целочисленного деления (деления по модулю), к сожалению, может возвращать отрицательные числа для положительных делителей. Вместо этого можно было бы воспользоваться функцией rem_euclid, но я не могу спокойно рекомендовать эту функцию, так как она, к сожалению, определена для отрицательных делителей. Мне следовало бы написать об этом отдельную статью…

Общее решение

Мы обнаружили аккуратную формулу для вычисления того, что нам нужно, но если бы мы были хоть чуть менее удачливыми, то такой формулы могло и не существовать. Хорошо было бы найти более общий метод решения подобных задач. В данном конкретном случае такой метод существует. Имеется лишь 3 × 3 = 9 пар входных значений. Поэтому результат для каждой ситуации можно, не мудрствуя лукаво, жёстко задать в коде:

let answers = HashMap::from([
    ("A X", 4),
    ("A Y", 8),
    ("A Z", 3),
    ("B X", 1),
    ("B Y", 5),
    ("B Z", 9),
    ("C X", 7),
    ("C Y", 2),
    ("C Z", 6),
]);

Теперь результат можно получать, просто использовав конструкцию вида answers[input]. Может показаться, что это — так себе решение, но это — подход, который вполне имеет право на жизнь. Мы точно знаем то, какие выходы соответствуют каким входам. Иногда самое простое или самое быстрое (либо в плане времени, потраченного программистом, либо в плане времени, нужного на выполнение кода) решение заключается в том, чтобы просто самостоятельно и полностью что-либо вписать в код, вместо того, чтобы вычислять это во время выполнения программы, пользуясь реализацией некоего алгоритма.

Идеальные хеш-функции

Вышеприведённое решение работает правильно, но его обобщённость не бесплатна. Оно использует полнофункциональную реализацию алгоритма хеширования строк. Поиск значения предусматривает прохождение по всему пути выполнения кода поиска по хеш-таблице (и что самое важное — по пути кода разрешения конфликтов при хешировании).

Можно отказаться от обобщённости ради значительного прироста в скорости, если воспользоваться идеальной (или совершенной) хеш-функцией. Это — специально сконструированная хеш-функция, работающая на некотором множестве значений S и устроенная так, что каждое значение из этого множества преобразуется, без коллизий, в разные выходные данные. Важно отметить, что нас заботит только поведение функции на входных данных из множества S, и что нас совершенно не интересуют результаты её работы с другими входными данными.

Минимальная идеальная хеш-функция — это такая функция, которая, кроме прочего, задаёт соответствие входных данных с плотным диапазоном целых чисел [0,1,…,|S|−1]. Это свойство может оказаться очень полезным, так как выход хеш-функции можно напрямую использовать для индексирования поисковой таблицы. Это, фактически, приводит к созданию хеш-таблицы, которая назначает соответствия значений из множества S с чем угодно, нужным разработчику. Но тут нет необходимости в строгой минимальности решения — до тех пор, пока разработчика устраивает то, что некоторый объём пространства хеш-таблицы будет потрачен нерационально.

Есть полностью обобщённые методы конструирования (минимальных) идеальных хеш-функций. Такие, как алгоритм Hash, displace and compress, реализованный в крейте phf. Правда, для этих методов характерна тенденция использовать поисковые таблицы для создания самих хешей. При работе с маленькими пространствами входных данных, где чрезвычайно важны скорость и размер, я добился успеха, просто пробуя разные подходы к решению задачи. Это может звучать как-то непонятно, потому что так оно и есть, поэтому позвольте мне вам всё это показать.

Чтение входных данных

Тут мы оставляем мир разумных решений ради обучения и развлечения. Мы, для простоты, не будем обрабатывать такие вещи, как переходы на новую строку в стиле Windows (rn) или некорректные входные данные.

Можно заметить, что каждая строка входных данных, получаемых от Advent of Code, состоит ровно из четырёх байтов. Это наблюдение позволит нам применить нечто вроде хака. Вот эти байты: одна буква — это выбор нашего оппонента, потом — пробел, потом — наш выбор, и в конце — байт, обозначающий переход на новую строку. Это значит, что мы можем просто прочесть строку входных данных в виде числа u32. Это чрезвычайно упрощает конструирование хеша в сравнении с его конструированием из строк.

Например, обращаясь к таблице ASCII, мы выясняем, что код символа A — это 0x41, код пробела — это 0x20, код символа X — это 0x58, а код символа новой строки — 0x0a. Это значит, что строка A Xn может быть представлена в виде целого числа 0x0a582041 (при условии, что мы работаем на машине с порядком байтов от младшего к старшему). Если вам неясно — почему 0x41 попадает в конец этого числа — помните о том, что у людей принято записывать числа так, что младшая значащая цифра располагается в их правой части.

Обратите внимание на то, что в системе с порядком байтов от старшего к младшему байты в числе u32 будут перевёрнуты, поэтому решение представить четыре байта в виде целого числа приведёт к появлению значения 0x4120580a. Вызов функции u32::from_le_bytes преобразует четыре байта, которые, как ожидается, расположены от младшего к старшему, в нативное целочисленное представление. На машине, где байты расположены от старшего к младшему, порядок следований байтов меняется, а на машине, где байты расположены от младшего к старшему, байты остаются в исходном виде. Правда, почти все современные процессоры используют порядок байтов от младшего к старшему. Поэтому, если преобразования не избежать, обычно рекомендуется писать код так, чтобы путь его выполнения, рассчитанный на порядок байтов от младшего к старшему, выполнялся бы быстро, а путь выполнения, рассчитанный на порядок байтов от старшего к младшему, предусматривал бы шаг преобразования.

Выполнение вышеописанных манипуляций со всеми возможными вариантами входных данных даёт нам следующее нужное нам соответствие между целыми числами:

Вход       LE u32      Ответ
-------------------------------
 A X       0xa582041       4
 A Y       0xa592041       8
 A Z       0xa5a2041       3
 B X       0xa582042       1
 B Y       0xa592042       5
 B Z       0xa5a2042       9
 C X       0xa582043       7
 C Y       0xa592043       2
 C Z       0xa5a2043       6

Исследование разных конструкций

Когда я говорил, что, решая задачу, просто пробую разные подходы, я именно это и имел в виду. Загрузим наши входные данные и соответствующие им выходные данные в Python и напишем тест:

inputs =  [0xa582041, 0xa592041, 0xa5a2041, 0xa582042,
           0xa592042, 0xa5a2042, 0xa582043, 0xa592043, 0xa5a2043]
answers = [4, 8, 3, 1, 5, 9, 7, 2, 6]

def is_phf(h, inputs):
    return len({h(x) for x in inputs}) == len(inputs)

Тут имеется девять входных показателей, поэтому, может быть, нам повезёт, и мы сразу же создадим минимальную идеальную хеш-функцию:

>>> [x % 9 for x in inputs]
[0, 7, 5, 1, 8, 6, 2, 0, 7]

Но, увы, тут у нас коллизии. Что если мы не стремимся к абсолютному минимализму?

>>> next(m for m in range(9, 2**32)
...      if is_phf(lambda x: x % m, inputs))
12
>>> [x % 12 for x in inputs]
[9, 1, 5, 10, 2, 6, 11, 3, 7]

Не так уж и плохо! Нерационально используемое пространство памяти соответствует лишь трём элементам. Создать нашу первую идеальную хеш-таблицу можно, разместив ответы в подходящих местах:

def make_lut(h, inputs, answers):
    assert is_phf(h, inputs)
    lut = [0] * (1 + max(h(x) for x in inputs))
    for (x, ans) in zip(inputs, answers):
        lut[h(x)] = ans
    return lut

Попробуем это:

>>> make_lut(lambda x: x % 12, inputs, answers)
[0, 8, 5, 2, 0, 3, 9, 6, 0, 4, 1, 7]

Применим простое сопоставление данных:

const LUT: [u8; 12] = [0, 8, 5, 2, 0, 3, 9, 6, 0, 4, 1, 7];

pub fn answer(x: u32) -> u8 {
    LUT[(x % 12) as usize]
}

Сжатие таблицы

Мы остановились здесь, на первом простом рабочем модуле, который, честно говоря, вполне в этом случае нам подходит, так как три байта нерационально используемой памяти — это довольно-таки неплохо. Но что если бы мы были не столь удачливы? Мы должны искать дальше. Даже хотя область значений функции, возвращающей остаток от деления на m — это [0, m), в применении к нашему набору входных значений, её образ может представлять собой меньшее подмножество значений. Исследуем некоторые из них:

>>> [(m, max(x % m for x in inputs))
...  for m in range(1, 30)
...  if is_phf(lambda x: x % m, inputs)]
[(12, 11), (13, 11), (19, 18), (20, 19), (21, 17), (23, 22),
 (24, 19), (25, 23), (26, 21), (27, 25), (28, 19), (29, 16)]

К сожалению, хотя это и вполне логично, при увеличении числа m наблюдается тенденция на увеличение максимального индекса. Но число 13, кроме того, выглядит многообещающим. Исследуем эту идею:

>>> [x % 13 for x in inputs]
[3, 6, 9, 4, 7, 10, 5, 8, 11]
>>> make_lut(lambda x: x % 13, inputs, answers)
[0, 0, 0, 4, 1, 7, 8, 5, 2, 3, 9, 6]

Так, так, так, не значит ли это, что нас посетила удача? Первые три индекса оказались неиспользуемыми, поэтому мы можем сдвинуть назад остальные индексы и получим минимальную идеальную хеш-функцию!

const LUT: [u8; 9] = [4, 1, 7, 8, 5, 2, 3, 9, 6];

pub fn answer(x: u32) -> u8 {
    LUT[(x % 13 - 3) as usize]
}

Как это ни парадоксально, но данная функция почти наверняка работает хуже, чем предыдущая. Теперь Rust необходимо проводить проверку выхода за границы диапазона, а предыдущая версия абсолютно надёжна. Тут, кроме того, используется дополнительная операция вычитания.

Мой опыт создания множества подобных сопоставлений говорит о том, что вы будете удивлены тому, как часто вас в подобных делах будет посещать удача — в том случае, если размер сопоставления будет не слишком велик. По мере того, как вы будете добавлять в свой набор инструментов больше «приёмов, которые надо попробовать», у вас будет и больше возможностей найти что-то подходящее.

Устранение «близких промахов»

Ещё один момент, который можно попробовать поправить — это «близкие промахи». Взглянем ещё раз на нашу исходную примитивную попытку:

>>> [x % 9 for x in inputs]
[0, 7, 5, 1, 8, 6, 2, 0, 7]

Коллизии создают лишь два последних входных значения. Существует один способ разрешения этих коллизий, хотя и примитивный, но вполне реальный. Заключается он в том, чтобы переместить эти значения на другой индекс:

>>> [x % 9 + 3*(x == 0xa592043) - 3*(x == 0xa5a2043) for x in inputs]
[0, 7, 5, 1, 8, 6, 2, 3, 4]

О, смотрите, нам опять немного повезло. И там и там используется константа 3, которую можно вывести за скобки. Очень затягивающими могут быть эксперименты, предусматривающие испытание различных преобразований операций и разных других приёмов для нахождения этих (минимальных) идеальных хеш-функций с применением минимально возможного количества операций.

Интерлюдия: целочисленное деление

До сих пор мы лишь использовали оператор деления по модулю для уменьшения пространства входных значений до намного меньшего чем то, что имелось изначально. Но целочисленное деление/деление по модулю — это операция, которая на большинстве процессоров выполняется довольно медленно. Если мы заглянем в таблицы инструкций Агнера Фога, то мы увидим, что 32-битная инструкция DIV занимает 9-12 циклов на AMD Zen3 и 12 циклов на Intel Ice Lake. Но нам не нужна универсальная инструкция деления, так как наш делитель — это константа. Посмотрим на то, что компилятор выдаёт для операции взятия остатка от деления на 13:

pub fn mod13(x: u32) -> u32 {
    x % 13
}

Вот результат:

example::mod13:
        mov     eax, edi
        mov     ecx, edi
        imul    rcx, rcx, 1321528399
        shr     rcx, 34
        lea     edx, [rcx + 2*rcx]
        lea     ecx, [rcx + 4*rdx]
        sub     eax, ecx
        ret

Компилятор преобразует операцию взятия остатка от деления в умножение с применением некоторых сдвигов / сложений / вычитаний. Для того чтобы понять то, как это работает — сначала давайте разберёмся с самой таинственной частью этой конструкции, с умножением на 1321528399, за которым следует сдвиг вправо на 34 бита. Интересующая нас «магическая константа» — это, на самом деле, , что означает следующие вычисления:

Для того чтобы доказать, что это, на самом деле, верно, мы отметим, что делится на 13, что позволяет разбить деление на две части. Первая — это правильный результат, вторая — параметр ошибки:

Затем мы исследуем параметр ошибки и заменяем как верхнюю границу, чтобы увидеть, что это никогда не влияет на результат после округления числа до ближайшего целого в меньшую сторону:

Я посоветовал бы тем, кто хочет лучше в этом разобраться, взглянуть на работу Integer division by constants: optimal bounds.

После вычисления производится вычисление нужного нам остатка от деления в виде с использованием такого тождественного равенства:

Компилятор уходит от использования другой (сравнительно) ресурсоёмкой операции целочисленного умножения путём использования инструкции lea, которая может вычислить a + kb, где k может быть константой 1, 2, 4 или 8. Вот как вычисляется :

Инструкция                   Перевод         Результат
lea     edx, [rcx + 2*rcx]   t := q + 2*q    t = 3q
lea     ecx, [rcx + 4*rdx]   o := q + 4*t    o = (q + 4*3q) = 13q

Инструкция LEA изначально предназначалась для вычисления индексов массивов, так как элемент arr[i] можно найти по адресу arr_start + sizeof(T)*i, а sizeof(T) очень часто является числом, представляющим небольшую степень двойки.

Смешивание битов

Мы видели, что техника выбора различных делителей оказалась рабочей, и то, что компиляторы используют умножение, реализуя деление по модулю с фиксированным делителем. Пришло время избавиться от посредника и перейти прямо к тому, что нам нравится — к целочисленному умножению. Для того чтобы лучше разобраться с тем, что именно происходит во время выполнения этой операции — мы можем умножить два целых числа, представленных в двоичной системе счисления, используя методы, о которых пишут в учебниках:

4242 = 0b1000010010010
4871 = 0b1001100100111 = 2^0 + 2^1 + 2^2 + 2^5 + 2^8 + 2^9 + 2^12

   Двоичное представление          Десятичное представление
               1000010010010   |   4242 * 2^0
              1000010010010    |   4242 * 2^1
             1000010010010     |   4242 * 2^2
          1000010010010        |   4242 * 2^5
       1000010010010           |   4242 * 2^8
      1000010010010            |   4242 * 2^9
   1000010010010               |   4242 * 2^12
-------------------------------|---------------- +
   1001110110100100111111110   |   20662782

У этого умножения есть одно прекрасное свойство, которым мы можем воспользоваться. А именно, все старшие биты результата умножения x∙c для некоторой константы c зависят, в основном, от битов x. То есть, при правильном выборе констант c и s, c*x >> s даст результаты, которые очень сильно отличаются друг от друга даже при небольших различиях обрабатываемого параметра х. Это — система для сильного смешивания битов.

Хеш-функции похожи на функции для смешивания битов, так как их создатели стремятся к тому, чтобы они были бы непредсказуемыми. Хорошую меру непредсказуемости можно найти, исследовав лавинный эффект. Применение настоящего «случайного оракула» приводит к тому, что изменение одного бита во входных данных даёт изменение всех выходных битов на противоположные с 50% вероятностью. Таким образом — зависимость всех выходных битов от входных данных — это хорошее свойство для хеш-функции, так как «случайный оракул» — это идеальная хеш-функция.

А если так — давайте просто кое-что попробуем. Мы остановимся на использовании делителя по модулю вида ради максимизации скорости (так как результат может быть вычислен с использованием двоичной операции AND вместо операции умножения) и попытаемся найти подходящие константы c и s. Нам нужно, чтобы область значений нашей функции имела бы размер , так как это — наименьшее число, представимое степенью двойки, превышающее 9. Мы будем использовать 32×32→32-битное умножение, так как нам нужно лишь 4 выходных бита, а 4 старших бита результата умножения достаточно сильно зависят от большинства битов входного значения. Выполнив сдвиг вправо на 28 битов для результирующего числа u32, мы ещё и получим без дополнительных усилий mod 2⁴.

import random
random.seed(42)

def h(x, c):
    m = (x * c) % 2**32
    return m >> 28

while True:
    c = random.randrange(2**32)
    if is_phf(lambda x: h(x, c), inputs):
        print(hex(c))
        break

Если надо больше, чем четыре бита выходных данных, или если не получается подобрать работоспособную константу — я попробовал бы 32×32→64-битное умножение, так как это даст больше выходных битов, с которыми можно работать.

Всегда немного волнительно нажимать на Enter, когда вслепую ищешь «магическую» константу, не зная о том, получишь ли нужный результат, или нет. В данном случае мгновенно был выведен результат 0x46685257. Так как код оказался таким быстрым — тут, вероятнее всего, будет много решений, поэтому мы, очевидно, можем проявить немного больше жажды наживы и посмотреть — можно ли ещё сильнее приблизиться к минимальной идеальной хеш-функции:

best = float('inf')
while best >= len(inputs):
    c = random.randrange(2**32)
    max_idx = max(h(x, c) for x in inputs)
    if max_idx < best and is_phf(lambda x: h(x, c), inputs):
        print(max_idx, hex(c))
        best = max_idx

Этот код быстро перебирает несколько решений, а потом находит константу, которая даёт минимальную идеальную хеш-функцию, 0xedc72f12:

>>> [h(x, 0xedc72f12) for x in inputs]
[2, 5, 8, 1, 4, 7, 0, 3, 6]
>>> make_lut(lambda x: h(x, 0xedc72f12), inputs, answers)
[7, 1, 4, 2, 5, 8, 6, 9, 3]

По иронии судьбы, если нам нужна оптимальная производительность при использовании Safe Rust (безопасного Rust), то нам нужно заполнять нулями пустые элементы массива, содержащего 16 ячеек, чтобы никогда не выйти за его границы. Но если вы абсолютно уверены в том, что среди входных данных не будет ничего, что не было заявлено заранее, и вы хотите добиться оптимальной скорости — вы можете снизить использование памяти до 9 байтов, пользуясь Unsafe Rust (небезопасным Rust). Применяя безопасный подход, мы получим следующее:

const LUT: [u8; 16] = [7, 1, 4, 2, 5, 8, 6, 9, 3,
                       0, 0, 0, 0, 0, 0, 0];

pub fn phf_lut(x: u32) -> u8 {
    LUT[(x.wrapping_mul(0xedc72f12) >> 28) as usize]
}

Исследуя ассемблерный код с помощью Compiler Explorer можно обнаружить, что теперь он весьма компактен:

example::phf_lut:
        imul    eax, dword ptr [rdi], -305713390
        shr     rax, 28
        lea     rcx, [rip + .L__unnamed_1]
        movzx   eax, byte ptr [rax + rcx]
        ret

.L__unnamed_1:
        .asciz  "0701040205b06t03000000000000"

Самая маленькая хеш-таблица в мире

Вы думаете, что самая маленькая хеш-таблица в мире — это 9 байтов? Да мы ещё и не начинали! Как видите — можно сделать маленькую поисковую таблицу, не обращаясь к памяти, храня её в коде.

Код, в итоге, должен быть сохранён в памяти, но этот подход избавляет нас от одного из уровней абстракции.

Особенно эффективный метод хранения маленьких поисковых таблиц с маленькими элементами — это использование константы, индексируемой с помощью сдвигов. Например, поисковую таблицу [1, 42, 17, 26][i] можно представить в таком виде:

(0b11010010001101010000001 >> 6*i) & 0b111111

Каждое отдельное значение помещается в 6 битах, что позволяет легко разместить 4 × 6 = 24 бита в числе u32. Само по себе это, возможно, и не выглядит как что-то такое, что лучше нормальной поисковой таблицы, но эту штуку можно скомбинировать с идеальных хешированием, а ещё её можно векторизовать.

К сожалению, у нас имеется 9 значений, каждое из которых нуждается в 5 битах, то есть — они не поместятся в число u32… или поместятся? Видите ли, скомбинировав поисковую таблицу с идеальной хеш-функцией, мы можем, в теории, перекрыть окончанием битовой строки одного значения начало битовой строки другого — в том случае, если мы напрямую используем выход хеш-функции в виде показателя, задающего количество позиций сдвига.

Обновление от 05.03.2023. Как справедливо заметил пользователь tinix0 с Reddit, наши значения нуждаются лишь в 4 битах, а не в 5. Я всё сам для себя неоправданно усложнил, добавив нулевой бит в начало каждого значения. Но и при таком подходе перекрытие битов нам всё ещё нужно — чтобы уместить в число u32 4 × 9 = 36 битов.

Можно было бы просто воспользоваться для хранения данных числами u64, но это слишком скучно, мы ведь всё же пытаемся создать самую маленькую из возможных хеш-таблиц.

Мы, таким образом, ищем две 32-битных константы c и d, которые позволят нам построить такую конструкцию:

d >> (x.wrapping_mul(c) >> 27)) & 0b11111 == answer(x)

Обратите внимание на то, что «волшебный» сдвиг теперь равен 32 — 5 = 27. Нам надо, чтобы 5 битов выходных данных попали бы под второй сдвиг, так как 2⁵=32.

Нам, к счастью, не нужно увеличивать пространство поиска, так как мы можем сконструировать d из c, просто поместив биты ответа в указанных позициях сдвига. В ходе экспериментов мы можем, кроме того, выяснить, подходит нам c или нет, проверяя биты и обнаруживая конфликты для разных входных данных. Повезёт ли нам?

def build_bit_lut(h, w, inputs, answers):
    zeros = ones = 0

    for x, a in zip(inputs, answers):
        shift = h(x)
        if zeros & (a << shift) or ones & (~a % 2**w << shift):
            return None  # Конфликтующие биты.
        zeros |= ~a % 2**w << shift
        ones |= a << shift
    
    return ones
    
def h(x, c):
    m = (x * c) % 2**32
    return m >> 27

random.seed(42)
while True:
    c = random.randrange(2**32)
    lut = build_bit_lut(lambda x: h(x, c), 5, inputs, answers)
    if lut is not None and lut < 2**32:
        print(hex(c), hex(lut))
        break

Это занимает секунду-другую, но мы находим решение!

pub fn phf_shift(x: u32) -> u8 {
    let shift = x.wrapping_mul(0xa463293e) >> 27;
    ((0x824a1847u32 >> shift) & 0b11111) as u8
}
example::phf_shift:
        imul    ecx, dword ptr [rdi], -1537005250
        shr     ecx, 27
        mov     eax, -2109073337
        shr     eax, cl
        and     al, 31
        ret

Мы смогли заменить полномасштабную хеш-таблицу весьма компактной конструкцией, которая состоит всего из 6 (векторизуемых) ассемблерных инструкций без каких-либо дополнительных данных.

Итоги

Да, это было безумное путешествие. Стоило ли оно того? Сравним четыре версии программы, основанные на хеш-функциях, проверим, сколько времени у них займёт обработка десяти миллионов строк различных входных данных и суммирование всех ответов.

1. hashmap_str — должным образом обрабатывает входные данные, воспринимая их в виде строк, заканчивающихся символом новой строки, как в обобщённом решении, описанном выше.

2. hashmap_u32 — всё ещё использует хеш-таблицу, но читает строки и выполняет поиск, используя числа u32 — так же, как делает идеальная хеш-функция.

3. phf_lut — ранний вариант функции, которая применяет поисковую таблицу и идеальную хеш-функцию.

4. phf_shift — это и есть самая маленькая в мире хеш-функция.

Полный код тестов можно найти здесь. На моём Apple M1 Macbook Pro 2021 года я получил следующие результаты, применяя Rust 1.67.1 и команду cargo run --release:

Получается, что это — не только самая маленькая хеш-таблица. Она ещё и самая быстрая. Она более чем в 180 раз быстрее исходной реализации HashMap, основанной на строках. Причина, по которой она на моей машине вдвое быстрее phf_lut, заключается в том, что она может быть полностью векторизована компилятором, а phf_lut требуется обращаться к данным в памяти, что либо невозможно, либо сравнительно медленно в векторизованном коде, в зависимости от того, какие SIMD-инструкции имеются в нашем распоряжении.

Результаты испытания этого кода, которые получатся у вас, могут отличаться от моих. Вам может понадобиться воспользоваться конструкцией RUSTFLAGS='-C target-cpu=native' для того чтобы автоматически векторизовать phf_shift.

О, а приходите к нам работать? 🤗 💰

Мы в wunderfund.io занимаемся высокочастотной алготорговлей с 2014 года. Высокочастотная торговля — это непрерывное соревнование лучших программистов и математиков всего мира. Присоединившись к нам, вы станете частью этой увлекательной схватки.

Мы предлагаем интересные и сложные задачи по анализу данных и low latency разработке для увлеченных исследователей и программистов. Гибкий график и никакой бюрократии, решения быстро принимаются и воплощаются в жизнь.

Сейчас мы ищем плюсовиков, питонистов, дата-инженеров и мл-рисерчеров.

Присоединяйтесь к нашей команде.