Итак, если еще не устали от цикла «Hello, RNA World» — ловите последнею статью сезона :)
В прошлой статье я обосновал, почему следует (или хотя бы целесообразно) отказаться от оценки энергии как целевой функции. Если кто не в курсе — целевая функция, это такая придуманная нами функция, по которой можно оценить приближаемся мы к поставленной нами цели или нет, т.е. «правильно» сворачивается РНК или нет.
Если энергия — это мало репрезентативная цель, тогда что более стабильно/чётче указывает куда двигаться? Если бы у нас была абсолютно формализованная и точная цель — это уже означало бы, что мы задачу решили, т.к. сама формализация целевой функции — есть не что иное как полноценное понимание процесса.
Но у нас такой роскоши нет. Мы вынуждены вначале выдвигать гипотезу — каким закономерностям подчиняется процесс, и определенным образом отражать это в целевой функции.
Еще раз о энергии, как целевой функции — в Rosseta@home для РНК, она была такая
SCORE = (VDW * 3.0 + RG) + (RNA_BS + RNA_BP_W + RNA_BP_H + RNA_BP_S) + (RNA_NONB * 1.5 + RNA_O2ST + RNA_PHOS) + (RNA_AXIS*0.2 + RNA_STAG * 0.5 )
расшифровывать не буду. Но важно, что это некая сумма вкладов различных предполагаемых действующих воздействий. В итоге получается нечто среднеарифметическое. И соответственно, и двигаемся мы к чему-то аморфному. Точных коэффициентов при параметрах, какой вклад делает тот или иной параметр — никто не даст. А вычислить их невозможно — мы ведь и строим целевую функцию. Гадать тоже не дело. Я вначале пытался — и выяснил, что большая половина попросту не дает серьезного вклада, а лишь отклоняет расчеты не туда куда нужно.
Поэтому я оставил вначале только VDW — это некий обобщенный коэффициент, по сути он показывает есть ли запрещенные ковалентные связи (что это обсуждали в первых статьях). И со временем заменил это просто на ответ да/нет, т.к. бывало, что другие параметры — иногда перевешивали — и в итоге в .pdb файле получались пересечения, которых быть не должно.
Далее помним, что я предлагал основываться только на образование водородных связей. Когда они образуются мы математически знаем без каких-либо надуманных вещей: расстояние и угол — все. Где в РНК они есть — мы тоже стабильно знаем. (точнее, это сейчас достаточно хорошо предсказывается, есть нюансы — но потом ).
На рисунке вторичная структура одного рибозима, который я взял для экспериментов
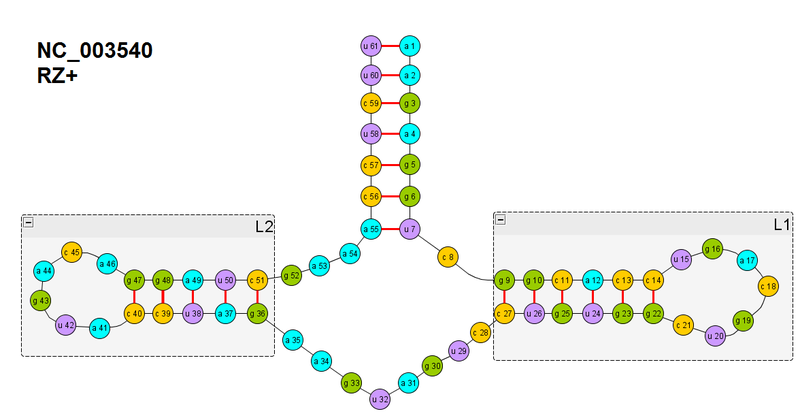
чтобы упростить себе жизнь, я начал с уже имеющейся гипотезы о том, что РНК/белки сворачиваются иерархически: т.н. Hierarchical model, которая имеет ряд вариаций, но суть такая: вначале начинают формироваться элементы вторичной структуры в развернутой цепи. Если сделать акцент на слове «начинают», то это вполне нормальная гипотеза, но иногда это понимают так, что полностью формируются вторичные структуры, а только потом происходит дальнейшие сворачивание. Но это нам будет важно потом, когда будем сворачивать рибозим полностью (сразу скажу, мне окончательно это еще не удалось — по моим критериям, а они получились жестче, т.к. основываюсь не на энергию, где не ясно минимум достигнут или можно еще лучше. Но к решению я похоже близок.).
А сейчас давайте свернем хотя бы маленький участок, образуем водородные связи между двумя нуклеотидами. Возьмем правую петлю cugacgucg (от 14 по 22) — 9 нуклеотидов и между крайними c-g образуем водородную связь.
Как построить целевую функцию?
Между c-g образуется 3 водородных связи, поэтому у нас есть три расстояния (r1, r2, r3) и три угла (a1, a2, a3). Чтобы функциям была говорящей, нам нужно, чтобы было так: если ее значение в итоге ноль и меньше — значит образовались все 3 водородные связи. А положительное значение должно плавно показывать приближение к этому состоянию.
Поэтому от текущих расстояний надо отнять 3 агстрема, а от углов 20 градусов. Получим значения, которые дают положительный вклад в функцию. Хотелось бы все эти 3 угла и 3 расстояния сплюсовать — и получим значение целевой функции. Но расстояния и углы плюсовать несерьезно — разные величины. Поэтому есть такой прием приведение к одному масштабу. Значимые расстояния (после вычитания 3) у нас где то от 1 до 12. Значимые в том смысле, что на этих расстояниях уже влияет угол. А если расстояние больше, то угол не важен: какая разница как повернуты атомы, если их разделяет пропасть. А углы у нас от 0 до 180, за минусов 20-ти = 160.
Если примерно прикинуть получается, что если расстояние умножить на 10, то расстояния и углы будут в одном масштабе. Поэтому делаем:
r1 -= 3.0f; r1 *= 10;
r2 -= 3.0f; r2 *= 10;
r3 -= 3.0f; r3 *= 10;
a1 -= 20;
a2 -= 20;
a3 -= 20;
Далее есть два варианта. Один
locScore = (r1 + r2 + r3 + a1 + a2 + a3)
и второй
if (maxR > maxA)
{ locScore = maxR; }
else
{ locScore = maxA; }
где maxR = максимум от (r1, r2, r3), а maxA = максимум от (a1, a2, a3)
Каждый из вариантов хорош по своему. Для начала сворачивания хорош второй. После наличия уже грубой структуры может пригодится и первый.
Ну а алгоритм очень простой: начинаем вращать (в части №3 — помним, что отобрали 1500 возможных поворотов) нуклеотиды с номерами
14
15
16
17
18 — тут например находится, что поворот с номером 210 самый лучший среди всех
19
20
21
22
вращаем скажем по двум углам №1 и №6 (т.е. №16). Найдя самый лучший фиксируем. Наша маленькая цепочка сложится надвое. Через какое-то время мы так загоним в «напряжение» (концы левый и правый стремятся соединится, а петля подвергается напряжению) нашу цепь, что по углам 1 и 6 она перестанет вращаться, и алгоритм зациклится. Как только он перестает давать лучшие состояние, меняем комбинацию углов, например, 3 и 4 (№34), и т.д. Это постепенно разгрузит напряжение по углам 1 и 6, и потом по ним можно будет еще попробовать «сжать».
Этого алгоритма вполне достаточно, чтобы требуемая водородная связь образовалась.
В следующей статье второго сезона :) поговорим о том, какие сложности появляются при образовании спирали целиком. Но еще пока одной спирали.
P.S. Очень рад, что к третей статье появились серьезные комментарии. Но одновременно похоже обыватель, потенциальный игрок FoldIt или просто поддерживающие био. распределенные вычисления — теряют интерес. Некоторую завершенную часть (Hello, RNA World) я рассказал. Дальше сложнее не будет, но возможно детали остального не так интересуют обывателей (напишите, если это не так). Я не скрываю, что ищу единомышленников и тех с кем можно проверять гипотезы, но в тоже время к массовости я еще не готов, и ПО тоже не готово. В общем кому это не безразлично пишите, я тогда быстрее созрею на сезон номер два.
Важный вопрос математикам:
Выше я описал две целевые функции
1. locScore = (r1 + r2 + r3 + a1 + a2 + a3)
2. if (maxR > maxA) { locScore = maxR; } else { locScore = maxA; }
Знаете ли вы как их объединить в одну? Т.е. скажем если 5 раз применяли первую целевую функцию, затем 5 раз применяли вторую и получили некий результат (понижение «энергии»). То надо, чтобы функция полученная после объединения, после ее применения 5 раз давала бы такой же результат как если применять первую и вторую по очереди. Возможно ли это?
Автор: tac






