Автоматический подбор синаптических весов. Самое начало. Циклический перебор

В одной из предыдущих статей (Синаптические веса в нейронных сетях – просто и доступно) мы разбирались со смыслом синаптических весов на примере определения цифры на 13-ти сегментном индикаторе и подбирали веса "вручную", путем логических рассуждений.

С этой статьи приступаем к автоматическому подбору и рассматриваем один из наиболее простых способов – циклический перебор.

В статье на конкретном примере поясняются некоторые термины машинного обучения (Логистическая функция, Softmax, One-Hot-Encoding, Квадратическая ошибка), представлены фрагменты кода и результаты в виде графиков и подобранных параметров.

Предыдущие статьи:
Синаптические веса в нейронных сетях – просто и доступно. Часть 1.
Синаптические веса в нейронных сетях – просто и доступно. Часть 2.

Программа в блокноте python:
Indicator13 - Google Colab Resarch Note
Доступно для сохранения и экспериментов.

Напомним, что имеем дело с задачей классификации.

Задача тестово-учебная: горят сегменты на 13-ти сегментном индикаторе (как на почтовом конверте), нужно определить цифру.

Если сегмент горит, то его значение равно 1, а если не горит, то 0.

Таблица коэффициентов состоит из 10 строк и 13 столбцов.
Строки соответствуют цифрам от 0 до 9, столбцы – номерам сегментов индикатора.

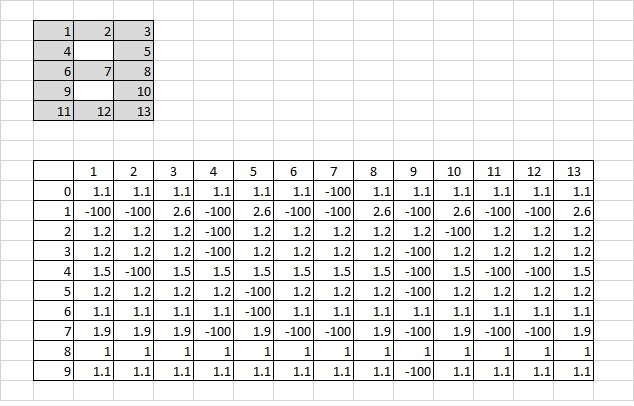
В предыдущих статьях описано, как коэффициенты подбирались "вручную" - таким образом, чтобы при построчном суммировании перемножений коэффициентов и значений сегментов максимальная сумма была бы в строке, соответствующей горящей цифре.

Другими словами, при умножении коэффициентов на значения соответствующих сегментов и последующем сложении получающихся значений построчно сравниваются суммы в строках - в какой строке сумма максимальна, та цифра и горит.

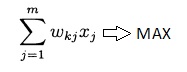
Переходим к автоматическому подбору

Начальная позиция

Подбор коэффициентов начинается с выбора начальных позиций.
Теоретически, можно начинать с того, что все коэффициенты равны 1, или все коэффициенты равны 0. В ряде случаев даже возможно все коэффициенты задать случайным образом. На данном этапе для данной задачи выбор начальной позиции не принципиален. Пусть все коэффициенты равны 0.  

Простой и логично понятный перебор

Общий алгоритм перебора коэффициентов можно описать тремя словами:
корректируем / суммируем / сравниваем.

 Возникают вопросы:
1. как понимать, что корректируем в нужную сторону
2. когда заканчивать

В общем случае, задача подбора коэффициентов сводится к задаче оптимизации, то есть когда нужно что-либо минимизировать или максимизировать.
Обычно максимизируют точность (правдоподобие), минимизируют ошибку.
Если ошибка уменьшается, то это значит, что коррекции идут в правильном направлении.
Когда показатели ошибки и точности достигают заданных величин - цель достигнута.

Тут нам понадобятся логистическая функция, Softmax и One-Hot-Encoding.

Логистическая функция

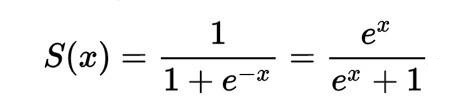
График логистической функции похож на букву S и ограничен по вертикали 0 и 1.

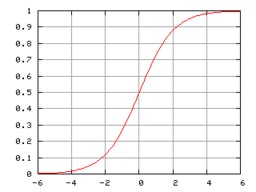
Логистическая функция удобна тем, что все значения после обработки попадают в интервал от 0 до 1, но сравнительное соотношение не меняется, то есть чем больше аргумент, тем больше значение функции. При этом чем больше аргумент, тем значение функции ближе к 1, а чем меньше аргумент, тем значение функции ближе к нулю. Все значения после обработки как бы загоняются в единый интервал, в котором удобно сравнивать. Сравниваются уже не десятки с сотнями или тысячами, а значения между 0 и 1.

Softmax

Теперь подберем функцию таким образом, чтобы сумма значений, которые уже находятся между 0 и 1 и которые мы сравниваем, стала бы равняться 1.
Такая функция была подобрана и получила название Softmax.

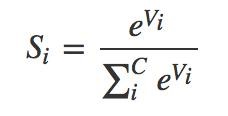
Softmax – очень распространенная функция для решения задач классификации, является как бы смысловым обобщением логистической функции.

Формально Softmax представляет собой отношение индекса текущего элемента к сумме индексов всех элементов (в другой формулировке - нормализует значения в вектор, следующий распределению вероятности). В определенной трактовке, Softmax преобразует значения в относительные вероятности, которые легче понимать и сравнивать. То есть так как все значения находятся между 0 и 1 и при этом сумма значений равна 1, то мы можем трактовать значения как вероятности.

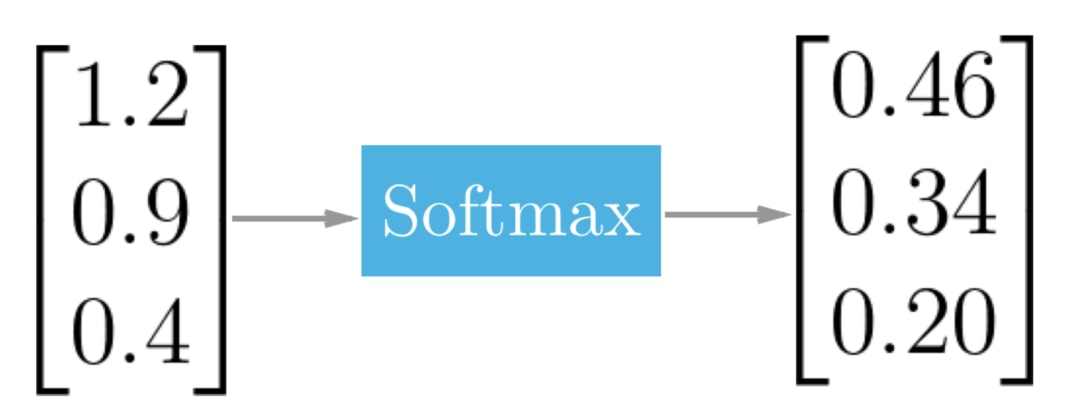
Можно трактовать так: вероятность того, что мы имеем дело с первым классом, составляет 46%, со вторым классом – 34%, а с третьим – 20%. Видно, что чем больше аргумент, то тем больше вероятность.

Если раньше мы сравнивали просто числа, то теперь мы сравниваем вероятности. Поначалу это кажется необычным, а по мере привыкания становится даже очень простым.

Вернемся к таблице.
Посчитаем построчно суммы для какой-нибудь цифры с учетом текущих коэффициентов и затем преобразуем значения сумм в каждой строке через Softmax.

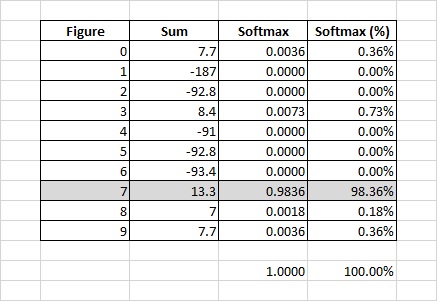
Если раньше сравнивали непосредственно значения, например, 8.4 (цифра 3) и 13.3 (цифра 7) и искали максимальное, то теперь сравниваем 0.0073 (цифра 3) и 0.9836 (цифра 7). И также ищем максимальное, логика не поменялась, но теперь несколько иначе трактуем. Теперь говорим, что вероятность того, что это цифра 3 – 0,73%, а вероятность того, что это цифра 7 – 98,36%, и выбираем цифру по максимальной вероятности.

Отметим, что на этапе подбора коэффициентов мы знаем правильный ответ. Нам остается только сравнить мнение модели с правильным ответом, а для этого привести мнение модели и правильный ответ к единому формату. В этом нам и поможет One-Hot-Encoding.

One-Hot-Encoding

Обычно мы воспринимаем цифры как 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Видоизменим их в массив длиной 10 (или 10-мерный вектор), состоящий из 0 и 1 так, чтобы индекс, имеющий значение 1, соответствовал цифре в привычном понимании.

0: Y = [1,0,0,0,0,0,0,0,0,0]
1: Y = [0,1,0,0,0,0,0,0,0,0]
2: Y = [0,0,1,0,0,0,0,0,0,0]
3: Y = [0,0,0,1,0,0,0,0,0,0].
4: Y = [0,0,0,0,1,0,0,0,0,0]
5: Y = [0,0,0,0,0,1,0,0,0,0]
6: Y = [0,0,0,0,0,0,1,0,0,0]
7: Y = [0,0,0,0,0,0,0,1,0,0]
8: Y = [0,0,0,0,0,0,0,0,1,0]
9: Y = [0,0,0,0,0,0,0,0,0,9]

Если мы возьмем, например, цифру 7 в таком коде, то в терминах предыдущего параграфа мы можем трактовать так: «Это цифра 7 с вероятностью 100%».

Теперь у нас есть два массива одинакового формата или два вектора одинаковой размерности - распределение вероятности и правильный ответ, и в таком случае возможно их сравнить и посчитать, насколько модель «ошиблась». 

Под ошибкой будем понимать разницу между фактическим выходным значением и правильным ответом. Прогноз модели, что вероятность цифры 3 равна 0.0073, означает, что ошибка равна 0.0073. Предположение, что вероятность цифры 7 равна 0.9836 означает, что ошибка равна -0.0164.

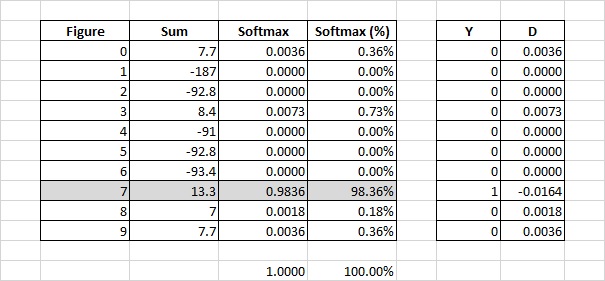
Общая квадратическая ошибка

Общая квадратическая ошибка – сумма квадратов ошибок для каждой цифры в каждой строке. Эту общую квадратическую ошибку и будем минимизировать.

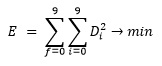
Формулы подробнее

Ошибка в каждой строке: D = Softmax(Sum) - Y

Для каждой цифры f и строки i:

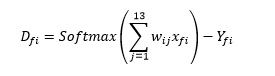
Ошибки могут иметь разные знаки, поэтому работаем с квадратами ошибок.

Суммируем квадраты ошибок для каждой цифры по каждой строке

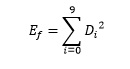
и затем суммируем получившиеся суммы квадратов ошибок по каждой цифре.

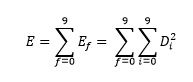
Таким образом получаем общую квадратическую ошибку модели при данном наборе коэффициентов.

Необходимо отметить, что часто величину ошибки усредняют, то есть делят на количество элементов, но так как количество элементов в данном случае величина постоянная, то на процесс оптимизации это никак не влияет. То есть можно использовать как общую квадратическую ошибку, так и среднюю.

Примечание:
Также для обозначения функции ошибки применяются следующие термины:
функция оценки, функция потерь, эмпирический риск.

Минимизация ошибки

Перейдем к перебору и минимизации ошибки

1. Зададим начальные веса, все равны 0:

K_array = np.zeros([10, 13])

2. Зададим матрицу значений сегментов индикаторов:

X = np.array([
  [1,1,1,1,1,1,0,1,1,1,1,1,1],
  [0,0,1,0,1,0,0,1,0,1,0,0,1],
  [1,1,1,0,1,1,1,1,1,0,1,1,1],
  [1,1,1,0,1,1,1,1,0,1,1,1,1],
  [1,0,1,1,1,1,1,1,0,1,0,0,1],
  [1,1,1,1,0,1,1,1,0,1,1,1,1],
  [1,1,1,1,0,1,1,1,1,1,1,1,1],
  [1,1,1,0,1,0,0,1,0,1,0,0,1],
  [1,1,1,1,1,1,1,1,1,1,1,1,1],
  [1,1,1,1,1,1,1,1,0,1,1,1,1]
  ])

3. Зададим массив правильных ответов:

Y = [0,1,2,3,4,5,6,7,8,9]

4. Преобразуем правильные ответы в нужный формат (One-Hot-Encoding):

#One-Hot_Encoding
Y_cat = np.zeros([10, 10])
for k in range(10): Y_cat[k][k]=1

# В Pythor есть специальная функция. Результат Идентичный.
# import tensorflow.keras
# Y_cat = tensorflow.keras.utils.to_categorical(Y, 10)

5. Зададим функцию Softmax:

def softmax(scores):
  softmax = np.exp(scores) / np.sum(np.exp(scores))
  return softmax

# В Pythor есть специальная функция. Результат Идентичный.
# from scipy.special import softmax

6. Зададим функцию подсчета общей квадратической ошибки:

def E():  
  array = np.zeros(10)
  Ef = np.zeros(10)
  Esum = 0
  for n in range(10):
    for i in range(10):
      array[i] = np.dot(X[n].T, K_array[i])   # умножаем вектор X на коэффиценты в строке
    array_soft = softmax(array)               # преобразуем через softmax    
    for k in range (10):
      Ef[n] += (array_soft[k]-Y_cat[n][k])**2 # суммируем квадраты ошибок в строкам
    Esum += Ef[n]                             # суммируем квадратические ошибки по каждой цифре
  return Esum

7. Зададим функцию коррекции коэффициента:

def choice():
  this_array = np.zeros(3)
  this_array[0] = E()
  K_array[n][k] = np.round(K_array[n][k] + lmd,2)
  this_array[1] = E()
  K_array[n][k] = np.round(K_array[n][k] - 2*lmd,2)
  this_array[2] = E()
  min = np.argmin(this_array)
  if min == 0: K_array[n][k] = np.round(K_array[n][k] + lmd,2)
  if min == 1: K_array[n][k] = np.round(K_array[n][k] + 2*lmd,2)
  return this_array

Здесь нужно отдельно пояснить.
Считаем общую квадратическую ошибку для трех вариантов:
·         для текущего состояния коэффициента
·         если к коэффициенту прибавить шаг lmd
·         если у коэффициента вычесть шаг lmd

При каком варианте общая квадратическая ошибка минимальна, такой коэффициент и устанавливаем.

8. Зададим функция подсчета точности:

def correct_count():
  correct = 0
  for n in range(10):
    array = np.zeros(10)
    for k in range(10):
      array[k] = np.dot(X[n].T, K_array[k]) # перемножение по каждой цифре
    array_soft = softmax(array)
    if np.argmax(array_soft) == Y[n]: 
      correct += 1
  return correct/10  

9. Зададим шаг изменения и количество полных проходов таблицы

lmd = 0.1
epochs = 10

10. И запускаем цикл перебора коэффициентов

for N_epochs in range(epochs):
  for n in range(10):
    for k in range(13):
      choice()                                # изменяем коэффициенты
    loss = E()
    accuracy = correct_count()    

Результат

На выходе получаем массив коэффициентов:

[[ 0.2  0.6 -0.9  1.   1.  -0.4 -1.  -0.4  1.   0.5  0.6  0.4 -0.9]
 [-1.  -1.   1.  -1.   1.  -1.  -1.   0.6 -1.   0.5 -1.  -1.   0.5]
 [ 0.6  0.5 -0.6 -1.   1.   0.2  1.  -1.   1.  -1.   0.6  0.3 -0.6]
 [ 0.1  0.9 -0.9 -1.   1.   0.7  0.9 -1.  -1.   1.   0.6  0.4 -1. ]
 [ 0.8 -1.   0.3  1.   0.6  0.6  0.8 -1.  -1.  -0.2 -1.  -1.   0.5]
 [ 0.2  0.6 -0.6  1.  -1.   0.5  0.7 -0.9 -1.   0.9  0.6  0.3 -0.7]
 [ 0.1  0.7 -0.7  1.  -1.   0.2  1.  -0.8  1.   0.3  0.2  0.2 -0.6]
 [ 1.   1.  -0.3 -1.   0.8 -1.  -1.   0.4 -1.   0.5 -1.  -1.   0.2]
 [-0.6  0.8 -0.9  1.   1.  -0.3  1.  -1.   1.   0.7  0.3  0.2 -0.9]
 [-0.6  0.7 -0.9  1.   1.   0.   0.9 -1.  -1.   0.8  0.7  0.6 -0.8]]

Можно посмотреть, как менялись величины точности и ошибки по мере прохождения перебора.

Начальная ошибка: 9.000000000000002
Начальная точность: 0.1

0: loss: 8.256888108456812 accuracy: 0.8
1: loss: 7.4035437200249845 accuracy: 0.8
2: loss: 6.515313270760133 accuracy: 0.8
3: loss: 5.655615573184693 accuracy: 0.8
4: loss: 4.889748309748125 accuracy: 0.9
5: loss: 4.243067834925036 accuracy: 0.9
6: loss: 3.6863744601447674 accuracy: 1.0
7: loss: 3.1957574183834616 accuracy: 1.0
8: loss: 2.7718738867787973 accuracy: 1.0
9: loss: 2.4043407365354073 accuracy: 1.0

Конечная ошибка: 2.4043407365354073
Конечная точность: 1.0 

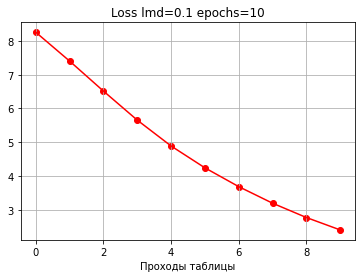
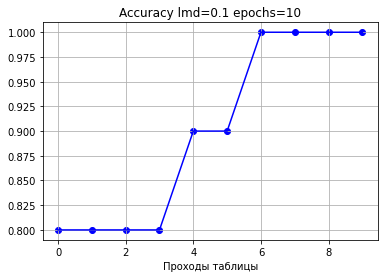
Видим, что с каждым проходом ошибка уменьшается, а точность растет.

Необходимо отметить, что даже если при изменении каждого коэффициента ошибка уменьшается, то точность не всегда растет. Встречаются случаи, когда ошибка уменьшилась, а точность тоже уменьшилась.

Если вывести на график величины точности при изменении каждого коэффициента, то видно, что точность иногда колеблется, но в целом постепенно движется вверх.

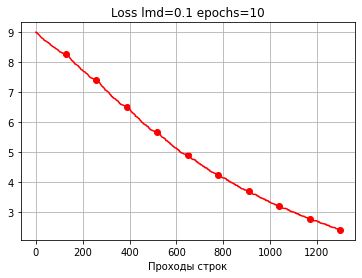
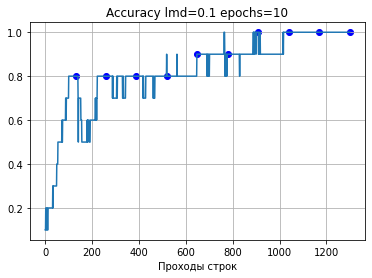
Важно понимать, что точность увеличивается как бы косвенно по мере уменьшения ошибки, поэтому недостаточно замерять только величину ошибки, надо смотреть именно на точность, то есть на тот показатель, который нам важен в конечном итоге.

# посмотрим результат

correct = 0
for n in range(10):
  array = np.zeros(10)
  for k in range(10):
    array[k] = np.dot(X[n].T, K_array[k])  # перемножение по каждой цифре
  array_soft = softmax(array)
  
  if np.argmax(array_soft) == Y[n]:        # сравниваем полученное и ожидаемое 
    correct += 1

  print(array_soft)
  print('Индекс:', np.argmax(array_soft)) 
  print('Ожидаемая цифра:', Y[n])
  print()

print('Точность:', correct/10)

Видим, что модель абсолютно корректно определяет цифры при заданном наборе сегментов.

Дополнение

Следует отметить, что первоначально шаг lmd=0.1 и количество проходов epochs=10 мы взяли наугад, как наиболее часто встречающиеся. И в данном случае 10 проходов хватило, чтобы достичь точности определения в 100%.

Если мы возьмем 50 проходов, то видим, что величина ошибки будет продолжать понижаться, хотя точность уже повышаться не будет, так как некуда.

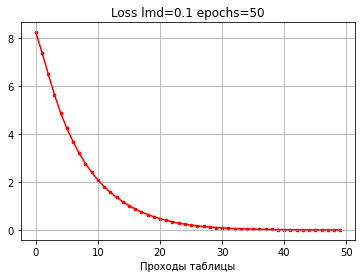
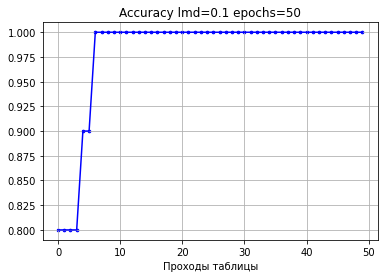
Для сравнительной демонстрации возьмем 10 проходов с шагом 1.

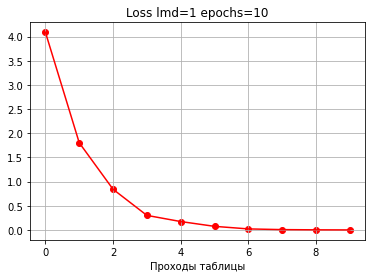
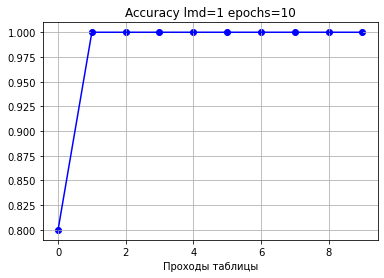
Видим, что ошибка уменьшается быстрее и точность растет быстрее, чем при шаге 1.
Уже после 2 проходов по таблице точность 100%.

И получили совсем другие коэффициенты:

[[  0.   0.   0.   1.   0.  -1. -10.   4.   3.   0.   0.   0.   0.]
 [-10. -10.  10. -10.   8. -10.  -9.   5.  -7.   0.  -8.  -8.   0.]
 [  2.   0.   0. -10.   3.   0.   0.   0.   3. -10.   2.   0.   0.]
 [  2.   0.   0. -10.   4.   2.   0.  -2. -10.   2.   1.   0.  -1.]
 [  6. -10.   4.   2.   1.   0.   0.   0. -10.   0. -10. -10.   4.]
 [  2.   1.   0.   1. -10.   3.   1.  -1. -10.   2.   0.   0.   0.]
 [  0.   0.   0.   1. -10.   3.   1.   0.   3.  -1.   0.   0.   0.]
 [  8.   8.  -2. -10.   1. -10. -10.   4. -10.   1. -10. -10.   2.]
 [  0.   0.   0.   1.   0.   0.   0.   0.   1.   0.   0.   0.   0.]
 [  2.   0.   0.   3.   2.  -3.   1.   0. -10.   1.   0.   0.   0.]]

Видим, что модель самостоятельно поставила большой отрицательный коэффициент (-10) похожим образом, где мы также закладывали большой минус (-100).

Итак, модель абсолютно корректно определяет цифры при заданном наборе сегментов.

Отметим, что здесь мы только начинали прицеливаться и брали шаг изменения и количество переборов практически наугад, примерно. При дальнейших улучшениях в программу целесообразно добавить параметры прекращения перебора. Например, чтобы программа прекращала перебор при достижении заданной величины точности или заданной величины ошибки. Также разумно добавить условие, что если ошибка не уменьшается или точность не растет заданное количество переходов, то увеличивать или уменьшать шаг изменения.

Важно, что, сейчас у нас была простая задача - мало параметров.
В действительных проектах параметров сильно больше, и простой перебор будет осуществляться очень долго. Для ускорения вычислений и переходов применяются различные оптимизирующие алгоритмы, но уже на этом примере видно, как в принципе обучается модель.

Предыдущие статьи:
Синаптические веса в нейронных сетях – просто и доступно. Часть 1.
Синаптические веса в нейронных сетях – просто и доступно. Часть 2.

Программа в блокноте python:
Indicator13 - Google Colab Resarch
Доступно для сохранения и экспериментов.