Современные нейронные сети достигли уже столь выдающихся результатов качества предсказаний, что компании начали встраивать их в свои процессы принятия решений.
ИИ сегодня водит автомобили, предсказывает болезни и распознаёт ваши налоговые декларации. Однако сами компании слишком мало говорят о том, почему предсказаниям нейронных сетей мы вообще можем доверять, умалчивая одну их занимательную особенность.
Уверенность
Проведём простейший эксперимент. Возьмём две нейросети: LeNet 1998 года и относительно современный ResNet 2016го.

Протестируем их на датасете CIFAR-100, после чего построим гистограммы распределений уверенности предсказаний для обеих моделей.
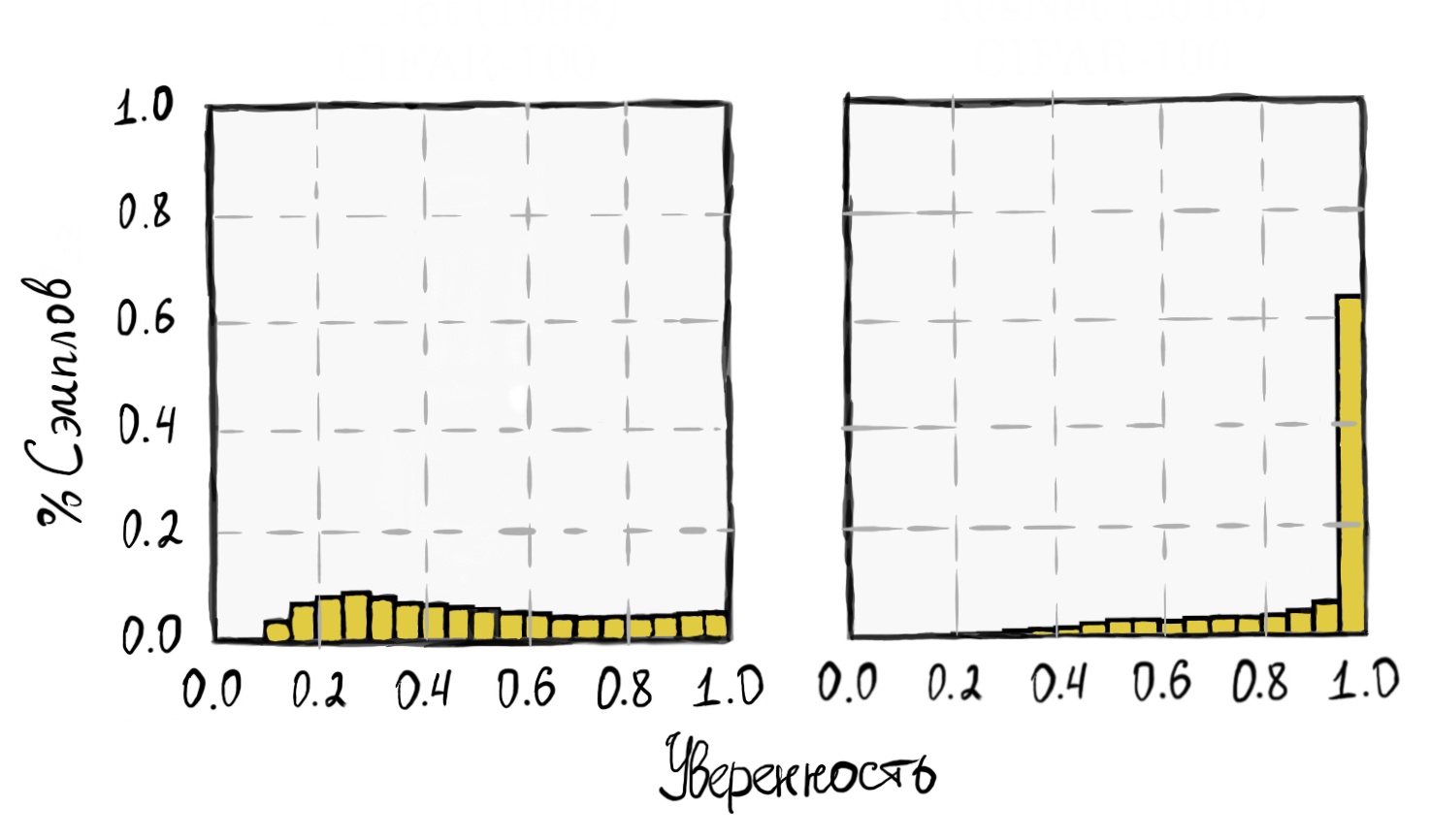
Легко увидеть, насколько сильно смещено распределение для ResNet сети. Более 60% изображений были предсказаны ей с уверенностью близкой к 100%. В то же время старушка LeNet показала относительную равномерность в своих предсказаниях.
Но давайте построим чуть более информативную штуку:
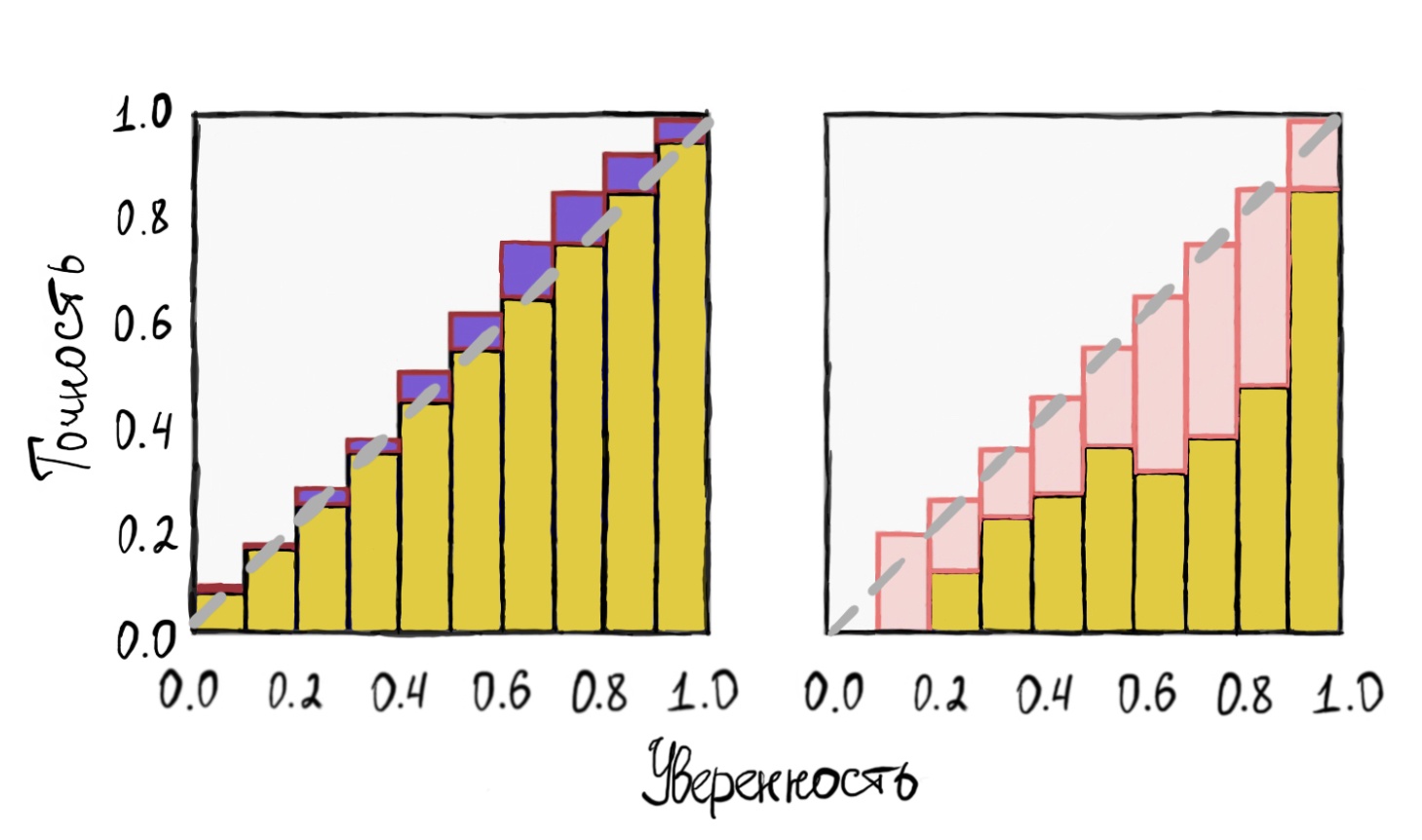
Данный график называется диаграммой достоверности (Reliability plot). Распределение по иксу разбито на 10ть бинов с шагом 0.1, а по игреку рассчитано относительное количество верно распознанных картинок, уверенность в предсказании которых входит в рассматриваемый бин.
Идеально нам хотелось бы видеть, к примеру, для бина [0.5-0.6] около 50% верно распознанных картинок с предсказанной уверенностью входящей в интервал. Для бина [0.9-1.0] уже порядка 100%. Т.е. мы хотим, чтобы(предсказанная уверенность была близка к вероятности).
Оптимальный уровень показан на рисунке серой диагональю. Относительно него и тут мы видим, как сильно современный ResNet проигрывает сети 1998го года в плане достоверности своих предсказаний.
Вероятность
Но почему же вообще уверенностьвероятность? Выясним на кошечках и собачках:

В глубоком обучении задача определения кошечка на картинке или собачка называется стандартно бинарной классификацией.
Взглянув архитектурно на решающие её сети, можно обнаружить в самом их конце два выходных нейрона. Один под класс "собака", второй для класса "кот".
Но этот пример самый популярный и наиболее показательный.
Во время обучения сеть оптимизируют так, чтобы при подаче в неё изображения, максимальный сигнал выходил из нейрона, соответствующего классу поданной картинки.
Далее эти сигналы из выходных нейронов попадают в функцию softmax, она переводит их в числа от 0 до 1, которые часто неверно интерпретируют как вероятности отнесения предсказания к классу.
![Самоуверенные нейросети - 9 begin{aligned} &left[begin{array}{l} 3.8 \ 0.4 end{array}right] Rightarrow softmax(z)=frac{e^{z_{i}}}{sum_{j=1}^{K} e^{z_{j}}} Rightarrowleft[begin{array}{l} 0.97 \ 0.03 end{array}right] end{aligned}](https://www.pvsm.ru/images/2022/07/10/samouverennye-neiroseti-9.svg)
Почему так делать не совсем корректно? Проблема в том, что вся суть функции softmax заключается в банальном переводе входящих значений сигнала, однако, к сожалению, этого не достаточно, чтобы данные числа стали вероятностями.
Да, сеть пытается подстроить входящие в функцию значения сигнала так, чтобы после преобразования получить числа близкие к единице для верно предсказанных классов. Но именно данное стремление и делает современные нейросети самоуверенными, банально поощряя модели давать уверенный предикт, что мы и видели на гистограмме выше.
Неуверенность
Решение обсуждённой выше проблемы в глубоком обучении называется калибровкой уверенности (Confidence calibration). В первой прикреплённой ниже статье вы сможете найти более детальное её описание и несколько методов решения проблемы, делающих предсказанные уверенности модели более близкими к вероятности. Стандартные методы выполняют это сближение путём выучивания некоторого преобразования уверенности на тестовой части выборки. Данный процесс и называется калибровкой.
Однако этот процесс не дарует сети одной важной способности. Способности говорить "я не знаю".
Что будет если в нашу нейронку с кошками и собаками подать иное животное? А если совсем не животное? В лучшем случае мы захотим увидеть предсказанную уверенность близкую к 0.5, однако с современными сетями этого ждать не приходится (распределение мы видели). Сеть просто выберет понравившейся ей класс из "кошка"/"собака" и выдаст приличную вероятность, она ведь уверена.
Но и эту проблему исследователи постепенно учатся решать. Данное направление в глубоком обучении называется оценкой неопределённости (Uncertainty estimation). Оценки неопределенности, полученные из модели, могут дать некоторое представление о достоверности конкретного предсказания. Это добавляет прозрачности алгоритму и сообщает нам о возможной неясности. Это особенно важно в приложениях, в которых критически важна безопасность решения.
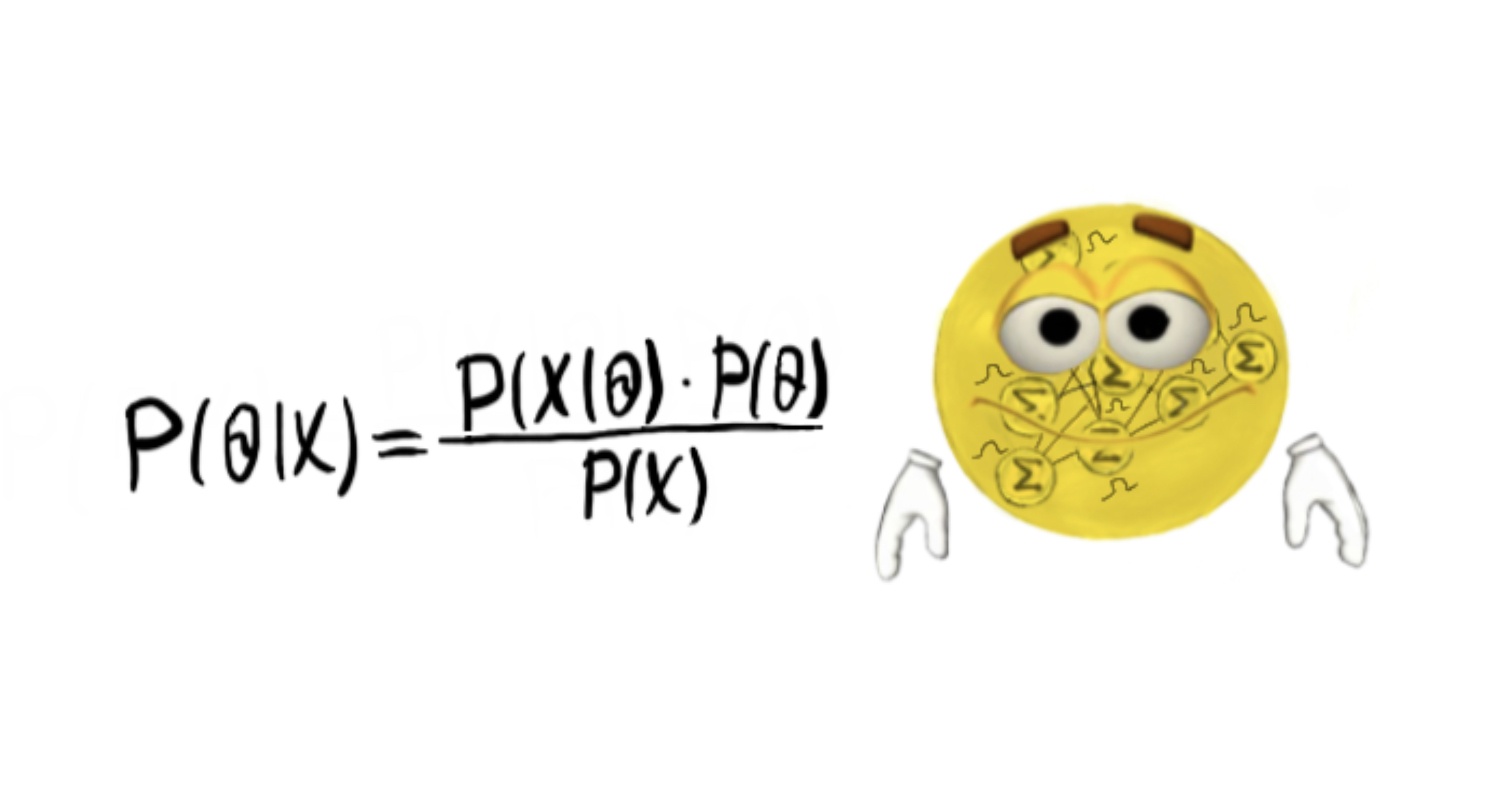
Наиболее теоретически честным методом оценки неопределённости являются байесовские нейронные сети. Это подкласс вероятностных моделей в глубоком обучении. В отличие от обычных сетей они представляют каждый отдельный свой вес не в виде числа, а моделируют его целым распределением.
Здесь я не буду мучать читателя принципами работы этих сетей и отошлю интересующихся к данной статье на Хабре. Скажу лишь, что хоть этот метод и хорошо обоснован теоретически, выдаёт приличные оценки неопределённости, но редко применяется на практике из-за сложностей в обучении и слабого качества предсказаний самих по себе.
Лучше детальнее обсудим несколько простых, но эффективных методов байесовской аппроксимации во время предсказания. Построенные на классических сетях их гораздо проще обучать, пусть они и требуют некоторых дополнительных ресурсов.
Большинство подобных методов основываются на идее создания искусственной вариативности предсказаний и дальнейшей их агрегации. Моделируя неопределённость в виде дисперсии, либо энтропии набора предиктов. Высокие значения неопределённости будут говорить нам о неуверенности сети: что ей был подан на вход сложный кейс, либо кейс, который она до этого не видела.
Ансамблирование в машинном обучении давно является популярной и мощной практикой для улучшения предиктивной способности модели. Однако, не совсем ясно, как это может помочь в задаче моделирования неопределенности.
Предлагается взять несколько независимых сетей, случайно инициализировать их веса, для каждой отдельной модели перемешать обучающий датасет и начать их параллельно обучать с подмешиванием так называемых состязательных примеров (слегка смещённых примеров из датасета, которые для сети будут уже являться новыми).
В итоге мы получим набор нейросетей, обученных на одинаковых данных, но имеющих различные веса. Посчитав дисперсию предсказаний сетей в ансамбле мы и получим нашу искомую оценку неопределённости.
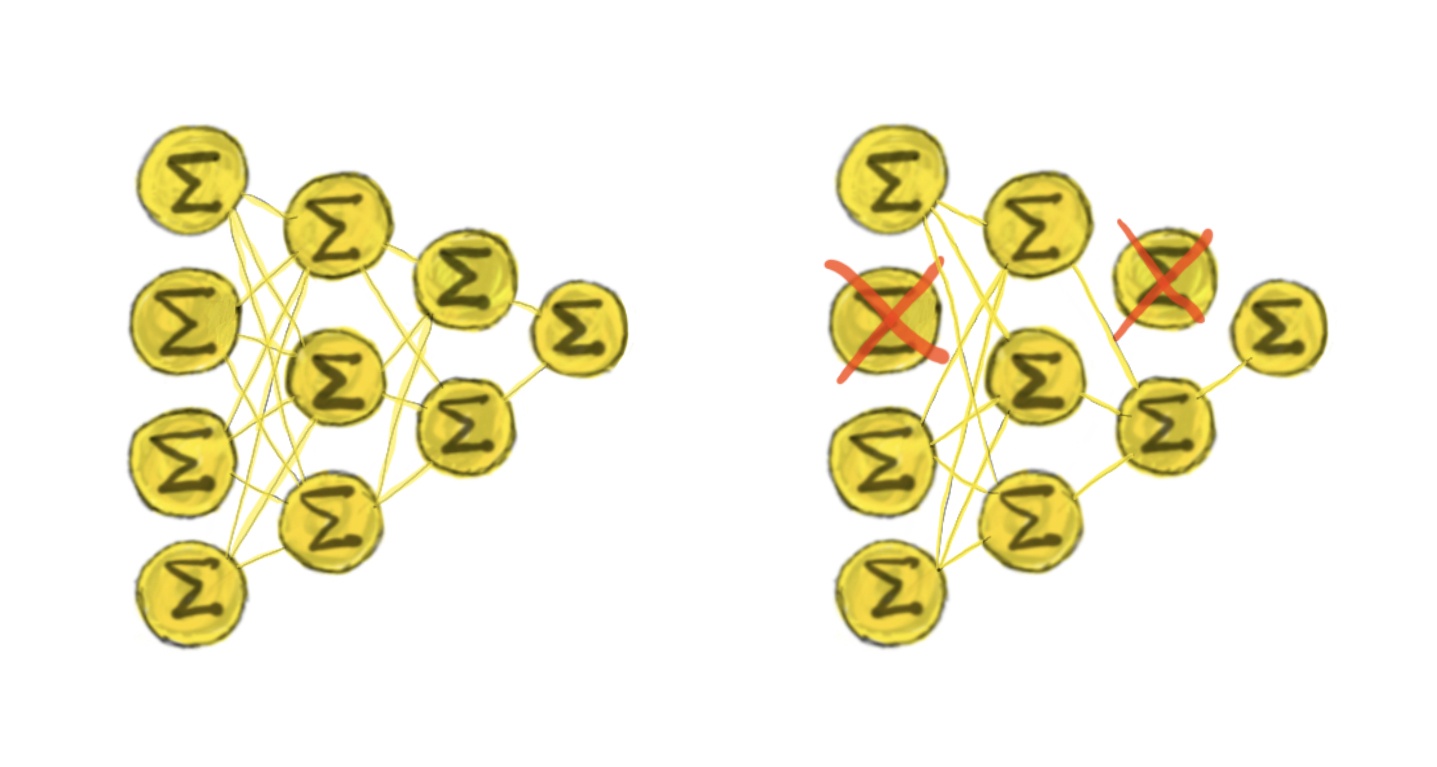
Слегка иной идеей является вариационный дропаут. Он работает в пределах одной сети, т.е. делит общие веса. Предлагается добавить в архитектуру нейросети большое количество dropout слоёв (слои, которые случайно выбрасывают какой-то процент нейронов при одном проходе, изначально применялись для регуляризации) и не выключать это поведение при предсказании. Это нам даёт возможность делать большое количество (сильно большее, чем для ансамбля) предсказаний, хотя они и будут сильно скоррелированны. Далее в ход идёт всё та же их дисперсия для моделирования неопределённости.
Итоги
В этой статье мы подсветили проблему слабой достоверности предсказаний нейронных сетей и их ограниченной применимости в приложениях с высокими требованиями к безопасности предсказаний. Обсудили два направления исследования данной проблемы: уверенность и неопределённость, рассмотрели несколько методов второго направления, а также обсудили вопрос оценки вероятности предсказаний.
В целом данная статья получилась скорее обзорной и больше для людей не из области глубокого обучения. Перед специалистами превентивно извиняюсь за малое количество математики и отсутствие кода :) Ждите от меня более детальный обзор недавнего state-of-the-art решения от DeepMind по тематике, там всё будет. Да и в рамках рассмотрения одного лишь метода должно получиться не так нагруженно, чем если всю математику выложить здесь. А пока читайте статьи, которые показались мне интересными по теме, подборка получилась обильной:
Список референсных статей (и не только):
Confidence estimation:
• On Calibration of Modern Neural Networks - базовая статья про оценку уверенности в современных нейросетях.
• Can You Trust Your Model’s Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift - большое хорошее исследование от Гугла по теме.
• Pitfalls of in-domain uncertainty estimation and ensembling in deep learning - отличная статья от русских исследователей из Samsung AI, исследует то, как правильно оценивать уверенность.
• Verified Uncertainty Calibration - побольше про калибровку от Стэнфорда.
• Confidence-Aware Learning for Deep Neural Networks - статья про внесение в функцию ошибки дополнительного элемента, учитывающего непосредственно уверенность.
Uncertainty estimation:
• Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles - основная статья про глубокие ансамбли.
• Dropout as a bayesian approximation: Representing model uncertainty in deep learning - основная статья про вариационный дропаут.
• Masksembles for Uncertainty Estimation - немного усовершенствованный вариационный дропаут с русскими авторами из EPFL.
• Dropout Distillation - статья про дистилляцию вариационного дропаута для ускорения работы.
• Enhancing the reliability of out-of-distribution image detection in neural networks - простой, но эффективный способ определения того, что сеть не видела поданные в неё данные (out of distribution детекция, был пример про иное животное для кошек/собак).
• Bayesian SegNet: Model Uncertainty in Deep Convolutional Encoder-Decoder Architectures for Scene Understanding - основная статья про оценку неопределённости в задаче сегментации.
• A Probabilistic U-Net for Segmentation of Ambiguous Images - объединение Unet и VAE, позволяет сэмплировать бесконечное количество масок сегментации и далее их агрегировать.
• PHiSeg: Capturing Uncertainty in Medical Image Segmentation - метод в сегментации создающий вариативность путём обучения сразу нескольких независимых голов.
• Medical Matting: Medical Images Segmentation with Uncertainty from Matting Perspective - ещё один метод для сегментации, объединяет оценку неопределённости с задачей матирования.
• Uncertainty-Aware Training of Neural Networks for Selective Medical Image Segmentation - последняя про сегментацию, внедряет идею с ранжирующим элементом в функции ошибки подобно упомянутой выше Confidence-Aware Learning for Deep Neural Networks.
• Confidence Prediction for Lexicon-Free OCR - оценка неопределённости в задаче распознавания текста.
• Robust Lexicon-Free Condence Prediction for Text Recognition - ещё одна про распознавание текста.
Other:
• Evidential Deep Learning to Quantify Classification Uncertainty - интересная идея, как предсказывать уверенность корректно и сразу.
• Epistemic Neural Networks - та самая недавняя SoTA от DeepMind.