Самая большая ошибка в истории физики

© 2018 HOWSTUFFWORKS

Сегодня мы обсудим одну из величайших нерешённых проблем фундаментальной физики — знаменитую катастрофу энергии вакуума. Что делает эту проблему такой увлекательной, так это то, что она сплетает воедино две самые успешные теории 21 века: квантовую теорию поля и общую теорию относительности, при этом демонстрируя, что что-то пошло катастрофически не так в нашей попытке понять происхождение расширения Вселенной. Чтобы разобраться, в чём собственно дело, нам придётся совершить путешествие по самым захватывающим идеям современной физики — от мельчайших квантовых флуктуаций вакуума до загадочной тёмной энергии, которая является движущей силой эволюции Вселенной.

Наша история начинается в двадцатых годах прошлого века в обсерватории Маунт-Вилсон. Она была оборудована рекордным на тот момент 100-дюймовым (2.5 м) телескопом, и одним из исследователей, которым выпала честь работать с инструментом, был Эдвин Хаббл. Первое умопомрачительное открытие состояло в том, что Вселенная не ограничивается нашей галактикой. Был идентифицирован ряд объектов слишком далёких, чтобы быть частью Млечного Пути, и некоторые известные «туманности» являлись в действительности отдельными галактиками за пределами нашей собственной. Конечно же, идея была принята в штыки консервативным научным сообществом, но под давлением накапливающихся наблюдательных фактов, скептики вынуждены были признать, что Вселенная куда больше, чем полагалось ранее.

Во-вторых, наблюдая за стандартными свечами, Хаббл заметил, что спектры многих объектов претерпевают красное смещение. Здесь сразу вспоминается эффект Доплера: если источник излучения или звука приближается к вам, то частота (излучения или звука) увеличивается, а при удалении — уменьшается, то есть сигнал смещается в более длинноволновую (красную) область. Но, что весьма странно, красное смещение зависело от расстояния — чем дальше находился объект, тем сильнее проявлялся эффект, и это работало во всех направлениях. Хаббл нанёс точки на график и уверенно провёл аппроксимирующую прямую:

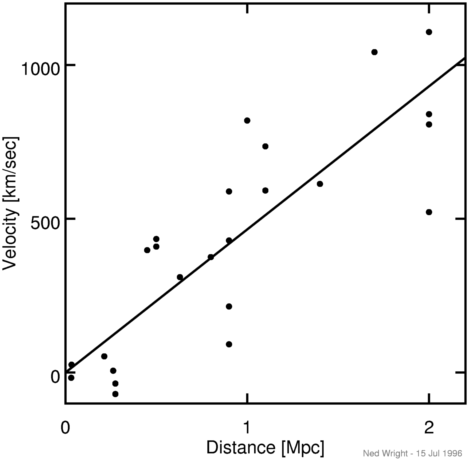
Наклон подогнанной линии составляет 464 км/сек/Мпк и этот параметр теперь известен как постоянная Хаббла H₀. Согласно полученному значению, космический объект, находящийся от нас на расстоянии в 2 мегапарсека, будет удаляться со скоростью около 1000 км/с! Поскольку и километры, и мегапарсеки (1 Мпк = 3e22 м) являются единицами измерения расстояния, можно выразить постоянную Хаббла в обратных секундах и выполнить грубую оценку возраста Вселенной:

Два миллиарда лет — слишком грубо! Мы знаем (и это было известно в 1929 году) благодаря радиоизотопному датированию, что возраст Земли больше 2 миллиардов лет, и эта несостыковочка привела к значительному скептицизму в отношении полученных Хабблом результатов, а последователи стационарной Вселенной получили передышку. Однако, более поздние работы показали, что Хаббл перепутал два разных типа переменных звёзд Цефеид, используемых для калибровки расстояний, а также то, что Хаббл считал яркими звёздами в далёких галактиках, в некоторых случаях на самом деле было областями ионизованного водорода. Коррекция этих ошибок привела к снижению значения постоянной Хаббла. В настоящее время существует в основном две группы, использующие Цефеиды и сверхновые типа Ia получившие 74.03±1.42 (км/с)/Мпк и 67.4±0.5 (км/с)/Мпк. Другие методы определения шкалы расстояний включают временную задержку в гравитационных линзах и эффект Суняева-Зельдовича в далёких скоплениях: оба не зависят от калибровки Цефеид и дают значения, согласующиеся со средним значением у других групп: 65±8 (км/сек)/Мпк. В совокупности множество различных методов дают фактический возраст Вселенной 13.7±0.2 млрд лет.

▍ Уравнения Фридмана для самых маленьких

Итак, куда не посмотри вглубь небосвода, обязательно найдётся галактика содержащая краснеющие и мутнеющие стандартные свечи. Самым очевидным предположением будет, что имеет место эффект старения света: чем дальше находится объект, тем дольше свет в пути и, возможно, во время распространения он постепенно переходит в длинноволновую область из-за пыли, диссипации в вакуум или ещё каких странных эффектов. Было предложено множество механизмов, но ни один из них не был в состоянии объяснить всю совокупность наблюдаемых явлений. Природа упорно указывала на разлёт галактик в разные стороны, и если откинуть вариант, что мы находимся в центре вселенной, то получалось разбегание всех от всех. Так что постепенно наиболее популярной моделью стала расширяющаяся Вселенная подчиняющаяся общей теории относительности.

Согласно этой модели, космологическое красное смещение в излучении наиболее далёких объектов обусловлено не эффектом Доплера в классическом понимании, а расширением самого пространства, из-за которого расстояние между любыми достаточно отдалёнными частями Вселенной увеличивается с течением времени. Модель применима к современной эпохе только для крупных структур (скоплений галактик и больших). На меньших масштабах материальные объекты связаны друг с другом силой гравитационного притяжения, и такие скопления не расширяются.

В основе современной космологии лежит космологический принцип. Этот постулат гласит, что при наблюдении в достаточно больших масштабах, распределение объектов во Вселенной выглядит одинаково для всех наблюдателей. Вселенная однородна и изотропна. Однородность означает, что свойства Вселенной везде одинаковы, а изотропия означает, что с любой заданной точки обзора, свойства Вселенной одинаковы в любом направлении. Теперь, учитывая, что Вселенная расширяется и что действует космологический принцип, мы хотим понять, как математически описать это расширение. Для этого мы рассмотрим очень большую сферическую область пространства, содержащую очень большое количество равномерно распределённых галактик:

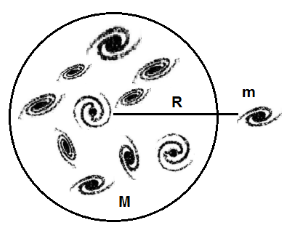
На одиночную галактику с малой массой, расположенную на краю сферы, согласно универсальному закону тяготения Ньютона действует сила:

Знак минус говорит, что сила, действующая на маленькую галактику, направлена к центру сферы. Далее вспомним второй закон Ньютона и выполним ряд преобразований:

где K — просто константа интегрирования. Первое слагаемое — половина квадрата скорости, является кинетической энергией на единицу массы, второе — это потенциальная энергия на единицу массы, и поэтому мы видим, что константа K представляет собой полную энергию на единицу массы. Другими словами, это уравнение — просто утверждение о сохранении энергии. Итак, давайте подумаем, что происходит, когда Вселенная расширяется и рассматриваемая область пространства увеличивается в размерах. Галактики будут удаляться друг от друга, и объём пространства, содержащего эти галактики, будет увеличиваться. Мы можем представить изменение радиуса сферы, содержащей галактики, с помощью того, что космологи называют сопутствующими координатами:

Получили ряд полезных соотношений, связывающих закон Хаббла (красное равенство) с масштабным фактором a. Этот множитель говорит, во сколько раз изменилось расстояние между космологическими объектами по прошествии некоторого времени. Также мы определили скорость расширения сферы, в которую заключено рассматриваемое скопление галактик. Выполним подстановку в наш закон сохранения энергии:

Здесь масса скопления галактик выражена в содержащейся в ней терминах плотности материи, а также использована известная формула для объёма сферы. Полученное уравнение известно как уравнение Фридмана в ньютоновой форме, поскольку мы вывели его, используя ньютонову механику. О чём говорит нам это уравнение? Прежде всего, отметим, что оно содержит скорость изменения масштабного фактора. Когда она положительна, рассматриваемая сфера расширяется и галактики разлетаются. Иначе будет стационарный или сжимающийся объём.

Хотя уравнение ньютоновской системы даёт полезную отправную точку для размышлений о расширении и сжатии сферической области пространства, оно не способно учесть динамическое искривление геометрии, предсказанное общей теорией относительности Эйнштейна, и поэтому, если мы хотим правильно понять расширение Вселенной, нам придётся использовать релятивизм. Хорошей новостью является то, что при выводе с помощью общей относительности общая структура уравнения Фридмана остаётся неизменной (подробный строгий вывод ищите в ссылкографии).

Появилась лишь пара новых параметров. Во-первых, мы ввели плотность энергии ε. Согласно общей теории относительности Эйнштейна, кривизна пространства-времени связана с наличием как массы, так и энергии, и, более того, вы можете думать о массе как о форме энергии. Второе изменение заключается в замене ньютоновой энергии эйнштейновской кривизной. Если вы помните, постоянная К, фигурирующая в ньютоновском уравнении, представляла собой полную энергию на единицу массы, и как только что было сказано, в теории Эйнштейна присутствие энергии влияет на кривизну пространства, и поэтому, когда мы выводим уравнение Фридмана, у нас появляется к (каппа) называемая кривизной и R₀ — радиусом кривизны.

▍ Кривизна Вселенной и критическая плотность

Одной из наиболее важных характеристик уравнения Фридмана является значение константы кривизны к, поскольку она определяет конечную судьбу Вселенной. Если каппа равна -1, то пространство считается отрицательно искривлённым, а правая часть уравнения Фридмана всегда положительна, и это описывает открытую Вселенную, которая будет продолжать расширяться вечно. С другой стороны, если каппа равна +1, то пространство положительно искривлено, и правая часть уравнения Фридмана в конечном итоге станет отрицательной, что приведёт к сжатию Вселенной, и такой тип решения называется закрытым. И, наконец, если каппа равна нулю, то мы имеем нулевую кривизну, и это описывает ситуацию, в которой Вселенная будет продолжать расширяться вечно, но с замедлением. Такая Вселенная, как говорят, плоская. Совершенно естественно, что одной из больших проблем в современной космологии, является определение значения каппы.

Как узнать, какой из этих трёх сценариев определит судьбу нашей Вселенной? Ну, первое, что нужно понять, это то, что если мы хотим применить уравнение к реальной вселенной, то нам нужно найти какой-то способ связать его с наблюдаемой и измеряемой величиной. К счастью, такая величина существует. Если вы помните, мы можем записать параметр Хаббла в терминах масштабного фактора , и поэтому допустимо переформулировать уравнение Фридмана:

Если мы сможем измерить значение параметра Хаббла в настоящий момент вместе с текущей плотностью энергии и кривизной, то в принципе мы должны быть в состоянии использовать уравнение Фридмана для определения судьбы вселенной. Как же измерить параметр Хаббла? Как мы уже видели, параметр Хаббла для нашей Вселенной в данный момент — это то, что мы называем постоянной Хаббла, и она может быть измерена путём наблюдения за красным смещением света от далёких галактик, и если мы используем самые современные измерения, то значение постоянной Хаббла составляет около 70 километров в секунду на мегапарсек (на каждые 3.3 млн световых лет). Мы также можем выразить постоянную Хаббла в базовых единицах си как . Поэтому давайте теперь используем это значение постоянной Хаббла для определения критической плотности Вселенной.

Что за критическая плотность? Как мы только что видели, если параметр кривизны каппа отрицателен, то Вселенная будет продолжать расширяться вечно, а если он положителен, то Вселенная, в конце концов, сожмётся, и поэтому ясно, что особый случай, когда каппа равна нулю, представляет собой критическую точку пересечения между открытой и закрытой Вселенной, и поэтому мы можем установить каппу равной нулю и выяснить, какое ограничение это накладывает на плотность энергии Вселенной.

Заметим, что критическая плотность зависит от значения параметра Хаббла в данный момент времени. Если плотность энергии Вселенной больше этого значения, то Вселенная выпуклая, а если меньше — то впуклая отрицательно искривлённая. Поскольку мы кое-как знаем текущее значение постоянной Хаббла, то находим современное значение критической плотности. Вышла величина эквивалентная примерно четырём атомам водорода на кубический метр. Может показаться, что это невероятно низкая плотность, однако следует помнить, что большая часть объёма Вселенной состоит из межгалактических пустот, где плотность чрезвычайно низка, и как мы увидим позже, средняя плотность наблюдаемой Вселенной, как оказалось, невероятно близка к критической плотности, но пока не будем забегать вперёд.

▍ Уравнение ускорения

Давайте вернёмся к нашему анализу расширяющейся Вселенной. Хотя уравнение Фридмана очень важно, оно не может само по себе сказать нам, как масштабный фактор изменяется со временем. Даже если у нас есть очень точные измерения современного параметра Хаббла и критической плотности, уравнение Фридмана по-прежнему остаётся уравнением с двумя неизвестными a и ε, обе из которых являются функциями времени. Нам нужно другое уравнение, включающее обе величины. Как мы уже видели, уравнение Фридмана в ньютоновском приближении является утверждением о сохранении энергии. В частности, говорится, что сумма гравитационной потенциальной энергии и кинетической энергии расширения постоянна. Сохранение энергии — в целом полезная концепция, поэтому давайте рассмотрим другое проявление той же идеи — первый закон термодинамики.

здесь dQ это поток тепла в или из рассматриваемой области, dU — изменение внутренней энергии системы, P — давление, а dV — небольшое изменение объёма. Теперь, если, как мы утверждали ранее, Вселенная идеально однородна, то для достаточно большого объёма пространства общий поток тепла в или из некоторой области будет равен нулю. Далее мы можем определить выражение для внутренней энергии в объёме пространства как равное плотности энергии в этой области, умноженной на объём области. Если мы предположим, что наша область пространства сферическая, то мы можем записать объём сферы как функцию от масштабного фактора. И, в конце концов, подставить всё в первый закон термодинамики:

Мы видим, что на правую часть этого уравнения наложено ограничение. Поскольку известно, что Вселенная расширяется, следует, что масштабный фактор a должен быть ненулевым, и поэтому для того, чтобы правая часть была равна нулю, придётся занулять выражение в скобках:

Это уравнение известно как уравнение жидкости, которое является просто альтернативным утверждением сохранения энергии, также как и уравнение Фридмана. Объединив эти два уравнения, мы можем получить уравнение ускорения, которое говорит нам, как скорость расширения вселенной меняется со временем.

Уравнение ускорения является одним из ключевых уравнений в космологии. Во-первых, обратите внимание, что если плотность энергии и давление положительны, то правая часть уравнения ускорения отрицательна, а значит, относительная скорость любых двух точек во Вселенной будет уменьшаться со временем, что приведёт к замедлению и сжатию Вселенной. Таким образом, согласно общей теории относительности Эйнштейна, положительное значение давления, вызванное тепловым движением атомов в газовом облаке, замедляет расширение Вселенной, а значит, уравнение ускорения подразумевает, что замедление и сжатие Вселенной неизбежно. Так как же объяснить положительно ускоряющуюся расширяющуюся Вселенную или, если на то пошло, статичную Вселенную?

Оказывается, это именно тот вопрос, над которым начал задумываться Эйнштейн после публикации своей первой работы по общей теории относительности в 1915 году. Тогда он, как и большинство физиков считал, что Вселенная статична. Но мы только что видели, что уравнение ускорения подразумевает, что Вселенная имеет отрицательное ускорение, и поэтому она неизбежно должна сжиматься, так что же сделал Эйнштейн? Ответ удивительно прост — Эйнштейн понял, что он может просто добавить положительное постоянное слагаемое в свои уравнения:

Если бы этот постоянный член точно соответствовал отрицательному вкладу плотности энергии и давления, то общее ускорение было равно нулю и Вселенная была бы статичной. В противном случае, если постоянный член достаточно велик, то общее ускорение будет положительным, и Вселенная будет ускоряться в своём расширении. Согласно распространённой среди современных исследователей интерпретации наблюдательных данных — именно это и происходит с нашей Вселенной. Поскольку эта константа относится ко всему пространству космоса, она стала известна как космологическая постоянная. Следует попытаться понять её роль и природу.

Для начала давайте сосредоточимся на нашем модифицированном уравнении Фридмана. Мы можем переписать его в более интуитивной манере, приведя все слагаемые к одной размерности:

Первое слагаемое мы разбили на плотность энергии материи и совокупного излучения (ещё иногда выделяют нейтрино, космические струны и прочие ужасы, но пока забудем о них). Также имеем плотности энергии, вызванные кривизной пространства и присутствием космологической постоянной. Как вы знаете, физики любят драматические названия, и они, конечно, не разочаровали, когда космолог-теоретик Майкл Тёрнер придумал термин «тёмная энергия» для описания таинственной плотности энергии, стоящей за ускоренным расширением нашей Вселенной.

▍ Судьба Вселенной

Космологическое уравнение Фридмана можно записать в удобной безразмерной форме:

где эпсилоны мы заменили безразмерными плотностями энергии омегами. Собственно, задача определения судьбы вселенной сводится к интегрированию этой дифурки для различных значений параметров плотности энергии. Рассмотрим ряд наиболее интересных решений:

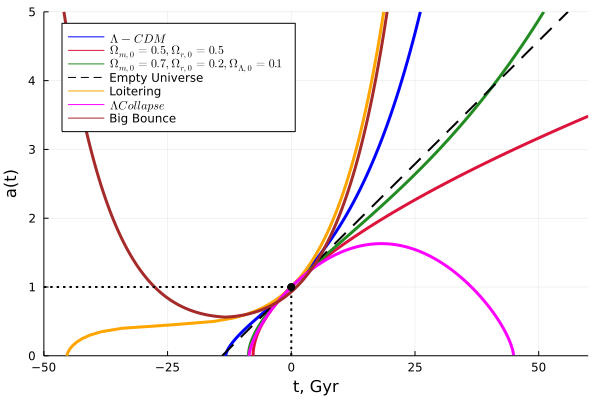
Красная линия — энергетический бюджет Вселенной представлен только материей и разбросанными между ней фотонами. Это близко к тому, что называлось вселенной Эйнштейна-де Ситтера. Она была стандартной моделью многие годы из-за своей простоты и отсутствия эмпирических доказательств пространственной кривизны или ненулевой космологической постоянной. Она также представляет собой важный теоретический случай вселенной с критической плотностью материи, находящейся как раз на пределе возможного сжатия. Вселенная расширяется вечно, но с замедлением.

В модели, показанной зелёной кривой, кривизна гиперболическая. Расширение тоже вечное.

Розовая линия соответствует сферической вселенной. Примечательно, что это самая молодая вселенная, возраст которой около восьми миллиардов лет. Эта вселенная в конечном итоге реколлапсирует в сингулярность. И в принципе, решение можно не ограничивать одним периодом — тогда вселенная живёт в бесконечном цикле схлопываний-больших взрывов.

Коричневая линия иллюстрирует сценарий «большого отскока». Вселенная как-то развивалась из большого взрыва, бесконечных осцилляций или ещё невесть чего, но потом начала сжиматься и разлетелась, миновав большой взрыв. Кто знает, может, будут найдены чёрные дыры, не согласующиеся с современными представлениями о возрасте Вселенной, тогда эта теория стала бы востребованной.

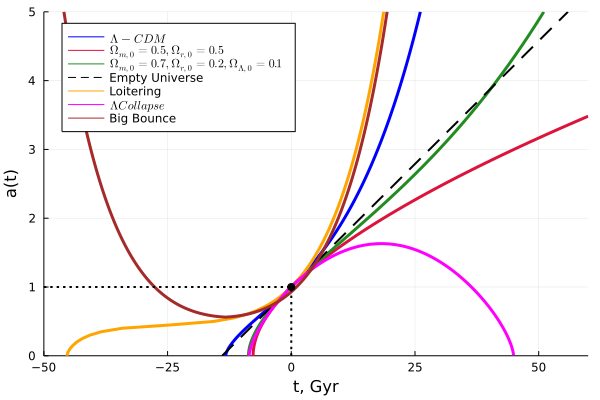
Другая возможность — это «блуждающая» (loitering) (также называемая вселенной Леметра) вселенная, которая показана оранжевой линией. Такая вселенная начинает жизнь из состояния с доминированием материи. Затем она вступает в стадию, при которой масштабный фактор является почти постоянным в течение длительного периода времени. После долгого безделья космологическая постоянная берёт верх, и Вселенная начинает экспоненциально расширяться.

Ну и синяя линия — это наиболее распространённая и освещённая в масс-медиа ΛCDM-модель: 70 порций тёмной энергии, 30 порций материи (по большей части тёмной) и немного фотонов, нейтрино и прочего мусора. Эта модель наиболее хорошо согласуется с современными представлениями о динамике крупномасштабных структур, распространённости химических элементов, c характеристиками реликтового излучения и с наблюдательными данными по удалённым объектам.

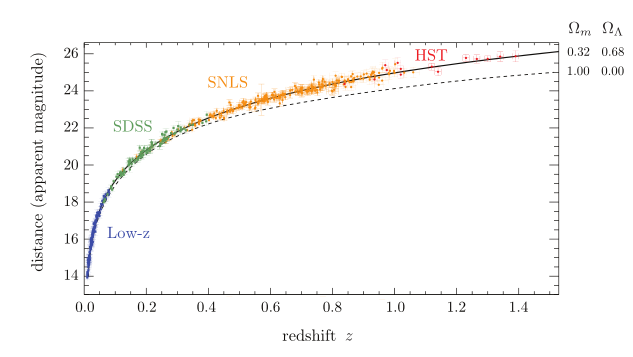
(SDSS = Sloan Digital Sky Survey; SNLS = SuperNova Legacy Survey; HST = Hubble Space Telescope.)

Здесь показаны совокупные данные от различных проектов по наблюдению сверхновых типа IA, и ΛCDM-модель даёт лучшие предсказания, чем теория не содержащая Λ-член. Хотя недавно было показано, «что с очень высокой вероятностью светимость этого типа сверхновых коррелирует с химическим составом и возрастом звёздных систем — а следовательно, применение их для определения межгалактических расстояний, в том числе для определения скорости расширения Вселенной — может давать ошибку».

▍ Природа тёмной энергии

В представленных выше сценариях развития Вселенной космологическая постоянная играла ключевую роль. Но какова причина этой плотности энергии? Короткий ответ — мы не знаем. Однако мы понимаем, что какова бы ни была причина, она должна быть в состоянии объяснить тот факт, что плотность энергии постоянна во всём пространстве, и это предполагает, что плотность энергии может иметь какое-то отношение к самому пространству. Оказалось, что согласно квантовой механике пустое пространство действительно имеет постоянную плотность энергии, и эта плотность энергии известна как энергия вакуума, поэтому если мы сможем определить плотность энергии вакуума, то мы сможем определить значение космологической постоянной и предсказать значение ускорения нашей расширяющейся Вселенной.

Но подождите секунду, разве вакуум по определению не пуст, и поэтому плотность энергии пустого пространства не должна быть нулевой? Как может быть, что пустое пространство содержит энергию? Как и многое другое в фундаментальной физике, ответ связан с принципом неопределённости Гейзенберга, поэтому давайте посмотрим на вакуум космоса глубже — на квантовом уровне. Существует предел того, насколько точно мы можем одновременно знать положение и импульс объекта, и эта неопределённость закодирована в известном соотношении ΔpΔx ≥ ħ/2 где ħ — постоянная Дирака, а Δx и Δp представляют собой неопределённость положения и импульса рассматриваемой системы.

Теперь, согласно самой успешной теории физики, квантовой теории поля, Вселенная наполнена множеством квантовых полей, которые пронизывают все пространство, и каждый тип частиц соответствует небольшой пульсации соответствующего поля. Поэтому электрон — это возмущение в электронном поле, а фотон — это пульсация в электромагнитном поле и так далее. Можно подумать, что согласно этой картине пустое пространство просто соответствует отсутствию частиц и, следовательно, возмущений, другими словами, вакуум состоит из квантовых полей с нулевой амплитудой. Именно здесь всплывает главная хитрость принципа неопределённости — если квантовое поле имеет точно нулевую амплитуду, то неопределённость в положении или амплитуде поля будет нулевой. Но мы видим, что это запрещено неравенством Гейзенберга, и поэтому придётся принять, что всегда есть присущее квантовому полю флуктуационное движение, и это движение вносит энергию, и именно эта энергия называется энергией нулевых колебаний.

В принципе, мы действительно можем измерить влияние этих вакуумных флуктуаций на энергию электрона внутри атома водорода и обнаружить, что это приводит к крошечному сдвигу на двух энергетических уровнях, известному как лэмбовский сдвиг. Это предсказание было экспериментально проверено с огромной точностью и представляет собой одну из величайших историй успеха стандартной модели физики частиц. А как же оценить энергию вакуума? Оказывается, количество энергии вакуума зависит от частоты вибрации лежащего в основе квантового поля.

Теперь, если мы хотим вычислить плотность энергии пустого пространства в результате вклада этих вакуумных флуктуаций, мы должны просуммировать все возможные частоты, соответствующие всем возможным вакуумным флуктуациям. Но ведь раз частота флуктуаций вакуума стремится к бесконечности, то и энергия этих флуктуаций будет бесконечной. Что же пошло не так? Дело в том, что в основе наших рассуждений прячется предположение о существовании бесконечно малых промежутков времени и пространства. И тут мы должны вспомнить про ограничение наших теорий на планковских масштабах.

Большинство физиков согласны с тем, что при использовании принципа неопределённости Гейзенберга для расчёта вклада в плотность энергии вакуума, мы должны использовать время Планка как темпоральную точку отсечения, ограничивающую максимальное количество энергии, которое может внести флуктуация вакуума. Эта энергия зовётся энергией Планка. Мы можем использовать её для вычисления максимально возможной плотности энергии, обусловленной квантовыми флуктуациями.

Для этого мы предположим, что количество энергии, равное планковской энергии, содержится в минимально возможном объёме пространства — планковской длине в кубе:

Если мы подставим числовые значения всех констант, то обнаружим, что предсказанная плотность энергии вакуума составляет приблизительно 10 в степени 114 джоулей на метр кубический, что является невероятно большой плотностью. Эта энергия имеет массу, эквивалентную примерно 10 в 97 килограммам на кубический метр, что действительно непостижимо. Это равносильно сжатию массы миллиарда триллионов триллионов триллионов галактик Андромеды в один кубический миллиметр, и вся эта энергия, как предсказывается, существует в результате квантовых флуктуаций, вытекающих из нашей самой успешной теории фундаментальной физики. Так как же это предсказанное значение сопоставляется с наблюдаемой плотностью энергии вакуума и, если на то пошло, как космологи экспериментально измеряют плотность энергии вакуума? Чтобы ответить на эти вопросы, давайте ненадолго вернёмся к уравнению Фридмана.

Мы видим, что есть три основных вклада в плотность энергии — это плотность, обусловленная содержанием материи во Вселенной, предположительная плотность энергии вакуума, которую мы только что обсуждали, и слагаемое, которое мы можем свободно интерпретировать как плотность энергии, обусловленную кривизной пространства. Одной из больших задач экспериментальной космологии является измерение значений этих трёх вкладов в общую плотность энергии Вселенной. За последние несколько десятилетий было использовано несколько различных методов для измерения и ограничения возможных значений этих параметров. В частности, наблюдение светимости сверхновых типа Ia вместе с измерениями небольших неоднородностей в космическом микроволновом фоновом излучении наложили жёсткие ограничения на измеренные значения плотности энергии.

В настоящее время, согласно самым последним экспериментальным данным, плотность энергии, обусловленная содержанием материи во Вселенной, составляет примерно 30 процентов от критической плотности, в то время как плотность энергии, обусловленная кривизной пространства, близка к нулю. Другими словами, кажется, что Вселенная пространственно плоская и что параметр каппа, с которым мы столкнулись ранее, равен нулю. Наконец, измерение ускорения расширения Вселенной предполагает, что плотность энергии за счёт тёмной энергии составляет около 70 процентов от критической плотности и поэтому мы видим, что если сложить все вклады, то общая плотность энергии Вселенной на самом деле удивительно близка к критической плотности и поэтому кажется, что мы живём в тонко сбалансированной пространственно плоской Вселенной.

Стоит также отметить, что детальные измерения скорости вращения галактик показывают, что на долю видимой материи приходится лишь около четырёх процентов энергетического содержания Вселенной, в то время как около 26 процентов этого содержания обусловлено присутствием тёмной материи. Как следует из названия, это материя, невзаимодействующая со светом, и поэтому мы не можем её увидеть. Подробное обсуждение тёмной материи вынесем в следующую статью, но сейчас важно сосредоточиться на том, что в плотности энергии нашей вселенной полностью доминируют тёмная материя и тёмная энергия, тогда как видимая материя, содержащаяся во всех звёздах и галактиках и в нас с вами, составляет лишь крошечную долю. Так как же измеренное значение плотности тёмной энергии сопоставляется с теоретическим значением, которое мы рассчитали ранее?

Если вы помните, предсказанное теоретическое значение было ошеломляющим — 10 в степени 114 джоулей на метр кубический, тогда как измеренное значение составляет примерно 70 процентов от критической плотности энергии, которая составляет около 10 в минус 10 джоулей на метр кубический, и таким образом, мы видим, что предсказанное значение в 10 в степени 124 раз больше, чем измеренное. Это, без сомнения, худшее несоответствие между предсказаниями и наблюдениями в истории физики, и именно это несоответствие лежит в основе одной из величайших нерешённых проблем фундаментальной науки — так называемой проблемы космологической постоянной, также известной как вакуумная катастрофа. Катастрофичность заключается в том, что Вселенная, подчиняющаяся предсказаниям нашей теории, должна удваиваться в размерах за каждое мгновение немногим большее, чем планковское время. И всё должно было быть разорванным на части в первые же моменты существования Вселенной.

▍ Решение проблемы

Что-то явно не так, но трудно определить, где именно ошибка. Очевидно, что приведённый выше вывод основывается на многих предположениях. Например, мы предположили, что Вселенная однородна и изотропна и что гравитация хорошо описывается общей теорией относительности. Это означает, что априори проблема космологической постоянной существует только в этом контексте. Мы также неявно предположили, что причиной ускоренного расширения является энергия вакуума, в чём можно было бы усомниться. На самом деле, можно построить модели, в которых Вселенная ускоряется из-за какого-то нового источника материи. Это, например, случай моделей квинтэссенции и/или галилеонов, где за ускорение отвечает скалярное поле. Однако это не решает проблему космологической постоянной, поскольку, даже если источником ускорения является некая таинственная субстанция, у нас всё равно остаётся проблема несоответствия плотности энергии вакуума критической плотности. Даже если тёмная энергия не является космологической постоянной, наблюдение, что плотность энергии сегодня является критической плотностью энергии, сильно ограничивает значение лямбда-члена.

С другой стороны, есть один очень простой способ решить эту проблему. Можно было бы предположить, что квантовое значение энергии вакуума по существу является поправкой к уже существующему классическому значению. Другими словами, мы просто утверждаем, что измеренное значение космологической постоянной является разницей между классическим и квантовым вкладом. Просто так совпало, что квантовый и классический мир компенсируют друг друга с точностью до 124 знаков после запятой. После утверждения о такой тонкой настройке некоторые начинают говорить что-то про разумного творца, но большинство останавливаются на пресловутом антропном принципе — вселенных, дескать, много, а мы в той, что по параметрам подошла. Для любителей теории струн и многих вселенных тонкая настройка должна быть приемлемым вариантом.

Иные предложения предполагают модификацию гравитации с целью отказа от общей теории относительности. Эти предложения сталкиваются с тем препятствием, что результаты наблюдений и экспериментов до сих пор, как правило, чрезвычайно хорошо согласуются с релятивизмом и ΛCDM-моделью. Кроме того, некоторые из предложений являются неполными, поскольку они решают проблему космологической постоянной, положив её значение равным нулю, а не крошечному числу, при этом не объясняя, почему квантовые флуктуации, по-видимому, не могут произвести существенную энергию вакуума.

Опять-таки существуют мнения, что проблема во многом надумана. Например, если тщательно учесть все тонкие эффекты (шутка ли, девять сотен формул отборной теории поля: arxiv.org/abs/1205.3365), то самая большая ошибка физики приблизится к 54 порядкам. А если плотность энергии квантового вакуума моделируется как флуктуирующее квантовое поле гравитирующее несколько иначе, чем представляется обычно, то проблема космологической постоянной просто не возникает ( arxiv.org/abs/1703.00543 +ответ (sci-hub), +ответ на ответ (sci-hub) ).

Так или иначе, статьи решающие проблему космологической постоянной появляются с завидной регулярностью. Вовсю идёт процесс генерации новых теорий, а всё более точные эксперименты их отсеивают. Так что с нетерпением ждём готовности «Джеймса Уэбба» вместе с прочими долгостроями и наслаждаемся происходящей научной революцией.

▍ Источники и материалы для дальнейшего погружения

• Dark Energy and the Vacuum Catastrophe
• Quantum Field Theory: What is a particle?
• Тёмная энергия во Вселенной
• wikipedia.org/ Cosmological constant problem
• Everything You Always Wanted To Know About The Cosmological Constant Problem
• Утечки энергии решили проблему космологической постоянной
• Тёмную материю и тёмную энергию заменили отрицательной массой
• Resolving the Vacuum Catastrophe: A Generalized Holographic Approach
• Ned Wright's Cosmology Tutorial
• Adventures in Friedmann Cosmology
• Ранняя вселенная 4. Кинематика однородной расширяющейся вселенной
• Космология. Подробный разбор решения Фридмана
• Краткая история Лямбды, или почему Итан привирает
• Визуализация решений уравнения Фридмана на julia и на python