Решение задачи транспортной логистики с помощью IBM CPLEX Solver

Всем привет!

Однажды меня попросили решить такую задачку в области транспортной логистики:

Есть грузовые машины, которые изначально готовы стартовать в разное время из разных географических точек.

Есть груженые рейсы, на которые нужны эти машины. Погрузка в среднем займет какое-то известное время, затем машина должна доставить груз в пункт назначения. Потом она может ехать на следующую погрузку и т.д.

Нужно написать математическую модель, которая скажет для каждой машины, на какую погрузку более оптимально её направить, чтобы максимально количество груженых рейсов было бы обслужено.

Поскольку я работала на тот момент с IBM CPLEX Solver, то его и взяла в качестве ядра решателя. А как я решала эту задачу – всё под катом.

Тип модели будет CP, т.е. оперировать будем интервалами.

Множества, которые даны по условию задачи

1. Доступные автомобили – cars

2. Географические точки, куда или откуда наши автомобили могут стартовать или приезжать, т.е. точки погрузки, старта, разгрузки. – points

3. Кортеж для хранения информации о старте машин - StartDateCar

<carId, carStartPoint, carStartTime>

carId – идентификатор машины

carStartPoint - точка начала движения машины

carStartTime - время начала движения каждой машины

4. Кортеж из 5 элементов для хранения данные о требуемых погрузках - Shipments:

<shipmentId, startShipmentTime, stratShipmentPoint, shipmentDuration, finishShipmentPoint>

shipmentId - идентификатор погрузки,

startShipmentTime – начало погрузки

stratShipmentPoint – географическая точка погрузки

shipmentDuration – время погрузочных работ

finishShipmentPoint – пункт назначения, т.е. куда нужно отвезти груз

Мы знаем, что машину ждут на погрузку к определенному времени. Если машина к этому времени не приехала, то и этот груженый рейс ей не достается.

Матрица

Поскольку мы знаем физические точки на карте, то можем посчитать расстояние, а также среднее время пути для автомобиля. Оформить и использовать эту информацию удобнее всего в виде матрицы. Столбцами и строками матрицы будут наши географические точки, а в ячейках матрицы будет храниться среднее время поездки из точки А в точку Б. Назовем матрицу DistanceMatrix.

Интервалы

Определимся, какими интервалами будем оперировать.

1. Интервалы начала доступности автомобиля

dvar interval StartInterval[c in cars] in startTimeCars[c]..startTimeCars[c] size 0;

2. Интервал погрузки и интервал разгрузки

dvar interval StartShippingInterval[c in cars][sp in shipmentIds] optional in stratShipmentTime[sp]..(stratShipmentTime[sp]+shipmentDuration[sp]) size shipmentDuration[sp];

dvar interval FinishShippingInterval[c in cars][sp in shipmentIds] optional size 0;

Последовательность

Объявим массив последовательностей для каждой машины. На них будут «жить» все наши интервалы. Получаем, что каждая последовательность из массива – это расписание для машины.

dvar sequence CarSequence[c in cars] in 
	append(
	all(a in {c}) StartInterval[a],
	all(sp in shipmentIds) StartShippingInterval[c][sp],
	all(sp in shipmentIds) FinishShippingInterval[c][sp]
	)
types append(  
	all(a in {c}) startPointCats[a],
	all(sp in shipmentIds) stratShipmentPoint[sp],
	all(sp in shipmentIds) finishShipmentPoint[sp]
	);

Мы видим, что в первой части нашей последовательности (sequence) объявляются множества интервалов, а во второй части (после types) объявляются типы этих интервалов. Так вот типами интервалов являются географические точки старта, погрузки и разгрузки соответственно. В этом и основная хитрость модели.

Ограничения модели

Теперь про ту самую «хитрость». В Cplex есть такая функция noOverlap, которая принимает на вход два параметра: последовательность (sequence) и матрицу переходов. И цель этой функции чтобы интервалы на последовательности не пересекались и минимальное расстояние между ними равнялось объявленному в матрице переходов. Вот эту функцию то и используем:

forall(c in cars)
	{
		noOverlap(CarSequence[c], DistanceMatrix);
	}

Матрица переходов хранит среднее время движения между физическими точками. Поэтому оптимизатор сам поймет, на какие погрузки машина не успеет доехать, а на какие успеет.

Остальные ограничения уже технические.

Ограничение, чтобы интервал старта машины был первым в соответствующе последовательности:

first(CarSequence[c], StartInterval[c]);

Ограничения, чтобы сохранить связность погрузки и разгрузки. Эти интервалы должны следовать строго друг за другом:

prev(CarSequence[c], StartShippingInterval[c][sp], FinishShippingInterval[c][sp]);

А так же если существует погрузка для этой машины, то должна существовать и разгрузка.

presenceOf(StartShippingInterval[c][sp]) == presenceOf(FinishShippingInterval[c][sp]);

Ну и нужно учитывать, что груженый рейс должна осуществлять только одна машина

sum (c in cars )presenceOf(StartShippingInterval[c][sp]) <= 1;
sum (c in cars )presenceOf(FinishShippingInterval[c][sp]) <= 1;

Цель модели

В задаче сказано, что нужно максимизировать количество обслуженных рейсов. То есть количество появления интервалов StartShippingInterval должно быть максимальным.

maximize sum(c in cars, sp in shipmentIds) presenceOf (StartShippingInterval[c][sp]);

Но в процессе тестирования появилась еще одна просьба по оптимизации: чтобы движение автомобилей было оптимальным. То есть нужно минимизировать лишние передвижения машин, и если машина уже стоит на какой-то точке и там вскоре будет погрузка, то оптимально использовать машину именно на этой точке.

Поэтому цель модели немного трансформировалось и вторым условием добавилось условие, чтобы минимизировать время между началом погрузки и окончанием предыдущего события. То есть порожних рейсов должно быть как можно меньше.

minimize staticLex(
	card(cars)*card(shipmentIds) - sum(c in cars, sp in shipmentIds) presenceOf (StartShippingInterval[c][sp]),
	sum(c in cars, sp in shipmentIds) (startOf(StartShippingInterval[c][sp]) - endOfPrev(CarSequence[c], StartShippingInterval[c][sp], 0, 0))
);

Анализируем результаты

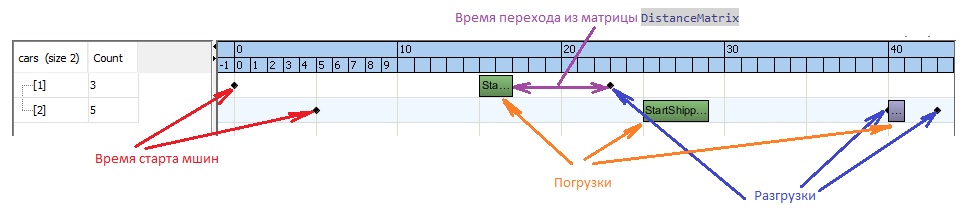
Создадим небольшой датасет из двух машин, четырех географических точек и трех груженых рейсов:

cars = {1, 2};
 
points = {1, 2, 3, 4};
 
 StartDateCar = {
 <1, 3, 0>,
 <2, 1, 5>
 };
 
// Shipments
 //int shipmentId; 
 //int startShipmentTime; 
 //int stratShipmentPoint; 
 //int shipmentDuration; 
 //int finishShipmentPoint; 

 Shipments = {
 <1, 25, 1, 4, 2>,
 <2, 15, 3, 2, 4>,
 <3, 40, 2, 1, 4>
 };
 
 DistanceMatrix = {
 <1,1,0>,<1,2,10>, <1,3, 6>, <1,4, 19>,
 <2,1,8>,<2,2,0>, <2,3,15>,<2,4,2>,
 <3,1,4>,<3,2,18>,<3,3,0>,<3,4,6>,
  <4,1,17>,<4,2,5>,<4,3,3>,<4,4,0>
 };

Вот такие результаты получаем:

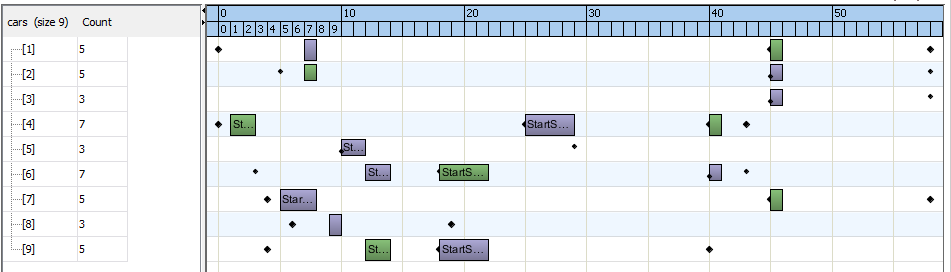
Добавим еще данных: Пусть будет 9 машин и 5 географических точек. Будем добавлять погрузки. Пусть их будет 25. Тогда первое решение тоже находит меньше чем за секунду, но наши 9 машин смогут обслужить только 17 груженых рейсов.

cars = {1, 2, 3, 4, 5, 6, 7, 8, 9};
 
points = {1, 2, 3, 4, 5};
 
 StartDateCar = {
 <1, 3, 0>,
 <2, 1, 5>
 <3, 5, 45>
 <4, 2, 0>
 <5, 4, 10>
 <6, 4, 3>
 <7, 2, 4>
 <8, 1, 6>
 <9, 3, 4>
 };
 
// Shipments
 //int shipmentId; 
 //int startShipmentTime; 
 //int stratShipmentPoint; 
 //int shipmentDuration; 
 //int finishShipmentPoint; 

 Shipments = {
 <1, 25, 1, 4, 2>,
 <2, 15, 3, 2, 4>,
 <3, 40, 2, 1, 4>
 <4, 45, 5, 1, 2>
 <5, 10, 4, 2, 1>
 <6, 12, 4, 2, 3>
 <7, 5, 2, 3, 5>
 <8, 45, 5, 1, 2>
 <9, 7, 1, 1, 5>
 <10, 16, 2, 1, 3 >
 <11, 1, 2, 2, 1 >
 <12, 18, 3, 4, 2>
 
 <13, 40, 2, 1, 4>
 <14, 45, 5, 1, 2>
 <15, 10, 4, 2, 1>
 <16, 12, 4, 2, 3>
 <17, 5, 2, 3, 5>
 <18, 45, 5, 1, 2>
 <19, 7, 1, 1, 5>
 <20, 16, 2, 1, 3 >
 <21, 1, 2, 2, 1 >
 <22, 18, 3, 4, 2>
 <23, 14, 3, 2, 1>
 <24, 6, 5, 3, 2>
 <25, 9, 5, 1, 4>
 };
 
 DistanceMatrix = {
 <1,1,0>,<1,2,10>, <1,3, 6>, <1, 4, 19>, <1, 5, 3>
 <2,1,8>,<2,2,0>, <2,3,15>,<2,4,2>, <2, 5, 12>
 <3,1,4>,<3,2,18>,<3,3,0>,<3,4,6>, <3, 5, 17>
  <4,1,17>,<4,2,5>,<4,3,3>,<4,4,0> <4,5, 9>
  <5,1, 3> <5,2, 12><5,3, 17><5,4,9><5,5,0>
 };

Вывод

Получили быструю несложную модель, которая рассчитает оптимальность груженых рейсов для нашего автопарка. Может быть полезна логистическим компаниям.

Модель

 using CP;
 execute PARAMS{cp.param.TimeLimit = 60;}
 
{int} cars = ...;
{int} points = ... ;

tuple startData {int carId; int carStartPoint; int carStartTime; };
{startData} StartDateCar = ...; 
int startPointCats[cars] = [ i.carId : i.carStartPoint | i in StartDateCar ]; 
int startTimeCars[cars] = [ i.carId : i.carStartTime | i in StartDateCar ]; 

tuple shipmentData {int shipmentId; int startShipmentTime; int stratShipmentPoint; int shipmentDuration; int finishShipmentPoint; };
{shipmentData} Shipments = ... ;

{int} shipmentIds = {i.shipmentId | i in Shipments};

int stratShipmentTime[shipmentIds] = [ i.shipmentId : i.startShipmentTime | i in Shipments ];

int stratShipmentPoint[shipmentIds] = [ i.shipmentId : i.stratShipmentPoint | i in Shipments ];
int finishShipmentPoint[shipmentIds] = [ i.shipmentId : i.finishShipmentPoint | i in Shipments ];

int shipmentDuration[shipmentIds] = [ i.shipmentId : i.shipmentDuration | i in Shipments ];


//--------------------
tuple triplet {int id1; int id2; int value;};
{triplet} DistanceMatrix = ...;
//-------------------------------------

dvar interval StartInterval[c in cars] in startTimeCars[c]..startTimeCars[c] size 0;

dvar interval StartShippingInterval[c in cars][sp in shipmentIds] optional in stratShipmentTime[sp]..(stratShipmentTime[sp]+shipmentDuration[sp]) size shipmentDuration[sp];
dvar interval FinishShippingInterval[c in cars][sp in shipmentIds] optional size 0;

//-----------------------------------
dvar sequence CarSequence[c in cars] in 
	append(
	all(a in {c}) StartInterval[a],
	all(sp in shipmentIds) StartShippingInterval[c][sp],
	all(sp in shipmentIds) FinishShippingInterval[c][sp]
	)
types append(  
	all(a in {c}) startPointCats[a],
	all(sp in shipmentIds) stratShipmentPoint[sp],
	all(sp in shipmentIds) finishShipmentPoint[sp]
	);


minimize staticLex(
	card(cars)*card(shipmentIds) - sum(c in cars, sp in shipmentIds) presenceOf (StartShippingInterval[c][sp]),
	sum(c in cars, sp in shipmentIds) (startOf(StartShippingInterval[c][sp]) - endOfPrev(CarSequence[c], StartShippingInterval[c][sp], 0, 0))
);

subject to
{
	forall(sp in shipmentIds)
		{
		  forall(c in cars)
		    {
		      
		      first(CarSequence[c], StartInterval[c]);
		      	      
		      presenceOf(StartShippingInterval[c][sp]) == presenceOf(FinishShippingInterval[c][sp]);
		      prev(CarSequence[c], StartShippingInterval[c][sp], FinishShippingInterval[c][sp]);
		    }
		    
		    sum (c in cars )presenceOf(StartShippingInterval[c][sp]) <= 1;
		    sum (c in cars )presenceOf(FinishShippingInterval[c][sp]) <= 1;
		}
			
			
	forall(c in cars)
		{
			noOverlap(CarSequence[c], DistanceMatrix, true);	  
 		}	  
}