
Кратко:
- Я модифицировал DOSBox для извлечения пар значений частоты/задержки мелодий PC-спикера из игры «Остров обезьян».
- Затем с помощью алгоритма Хаффмана я втиснул всю эту музыку в ATiny85 (512 байтов ОЗУ, 8Кб флэш).
- После этого собрал небольшую плату с динамиком для ее воспроизведения…
- … в качестве подарка моим племянникам и племянницам, с которыми встречусь в ближайшем будущем спустя год изоляции из-за пандемии.
Все верно – их дядя откровенный ботан, позаботившийся о том, чтобы детство племяшей не прошло без знакомства с Гайбрашем Трипвудом:)
Предыстория
Если вы…
- … счастливчик, игравший в «Остров обезьян» на ПК в далеких 90-х…
- … под аккомпанемент из примитивной, но при этом изумительной музыки PC-спикера…
- … обладаете таким же технически-ботанским складом ума, как я…
… то велика вероятность, что данный проект окажется вам по душе :)
В 1990 году я познакомился с Гайбрашем Трипвудом и отправился с ним в приключения на Карибы.
Для полной ясности скажу, что речь идет не о какой-то обыденной игре. Про «Остров обезьян» можно сказать очень многое – например то, что она вошла в список лучших игр за всю историю (если вы в нее не играли, то советую всерьез задуматься об этом).
Однако самое главное – это все же то, что она во многих отношениях является произведением искусства. В его лучшем виде.
И частью этого искусства была ее музыка, воспроизводимая PC-спикером!
Не удивительно, что старого нерда в конечном итоге потянуло «выкопать это сокровище»…
Кто бы мог подумать, что здесь можно найти даже футболку!
DOSBox
Сегодня даже наши повседневные телефоны являются суперкомпьютерами. По крайней мере такими они кажутся для парня, который в юности работал на ZX Spectrum.
Так что с точки зрения требований к ЦПУ эмулировать старые машины достаточно легко.
DOSBox является одной из программ, предназначенной именно для этого: она эмулирует DOS-машины практически идеально, позволяя старикам вроде меня заново проживать времена этой ОС и использовать оригинальную дискету с «Островом обезьян».
Поскольку DOSBox является открытым проектом, приключение началось с охоты на код, управляющий частотой PC-спикера. Задача оказалась относительно проста: в хороших старых ПК динамики управлялись программируемыми интервальными таймерами (PIT), так что после небольшого изменения кода DOSBox, отвечающего за обработку таймера…
//
// Тем временем...
//
// Внутри src/hardware/timer.cpp
//
//
case 0x02: /* Таймер подключился к PC-Speaker */
PCSPEAKER_SetCounter(p->cntr,p->mode);
+ // Раскрой мне тайны «Острова обезьян»!
+ printf("%.3g Hz @ %un",PIT_TICK_RATE/(double)p->cntr, PIC_Ticks);
break;
default:
LOG(LOG_PIT,LOG_ERROR)("PIT:Illegal timer selected for writing");… я заставил DOSBox выводить информацию о том, какую частоту он в данный момент воспроизводит через PC-скример.
Для правильного воспроизведения мне также потребовалось настроить измененный вариант DOSBox…
# В dosbox.conf
sb16=none
...
gus=false
...
pcspeaker=trueИ после запуска мутированного DOSBox с перенаправлением стандартного вывода я получил:
...
1.19e+06 Hz @ 15179
1.19e+06 Hz @ 15184
1.19e+06 Hz @ 15188
1.19e+06 Hz @ 15192
1.19e+06 Hz @ 15196
1.19e+06 Hz @ 15201
1.19e+06 Hz @ 15205
989 Hz @ 15209
989 Hz @ 15213
989 Hz @ 15218
784 Hz @ 15222
784 Hz @ 15226
784 Hz @ 15230
784 Hz @ 15234
658 Hz @ 15239
658 Hz @ 15243
658 Hz @ 15247
658 Hz @ 15251
494 Hz @ 15256
494 Hz @ 15260
494 Hz @ 15264
494 Hz @ 15268
392 Hz @ 15272
392 Hz @ 15277
392 Hz @ 15281
329 Hz @ 15285
329 Hz @ 15289
329 Hz @ 15294
329 Hz @ 15298
165 Hz @ 15302
165 Hz @ 15306
165 Hz @ 15310
...- 1.19МГц означает тишину.
- Остальное же чистая мелодия!
И поскольку это мелодия с временными метками, можно без проблем извлечь продолжительность каждой ноты.
Поэтому я быстренько набросал код Python для превращения этого цифрового сборника нот (из перенаправленного файла notes) в файл some.wav…
#!/usr/bin/env python
import os
FREQ = 22050
def emitSilence(f, ms):
print("Silence for", ms, "ms")
ms = 1 if ms > 5000 else ms
f.write(''.join([chr(0)]*int(22050*ms/1000)))
def emitFreq(f, freq, ms):
print("Emitting", freq, "HZ for", ms, "ms")
samples = int(FREQ/freq)
samples_on = int(samples/2)
data = [chr(255)]*samples_on
data += [chr(0)]*(samples - samples_on)
time_of_one_period = 1000. * samples/FREQ
while ms > 0:
f.write(''.join(data))
ms -= time_of_one_period
def main():
f = open("some.raw", "wb")
freq, tick = 0, 0
oldFreq, oldTick = -1, 0
for line in open("notes"):
freq, tick = line.split('Hz @ ')
tick = int(tick.strip())
freq = int(float(freq))
if freq != oldFreq:
ms = tick-oldTick
if oldFreq in (-1, 1190000):
print("Silence", ms)
emitSilence(f, ms)
else:
print("Freq", oldFreq, ms)
emitFreq(f, oldFreq, ms)
oldTick = tick
oldFreq = freq
f.close()
os.system("sox -r 22050 -e unsigned -b 8 -c 1 some.raw some.wav")
os.unlink("some.raw")
if __name__ == "__main__":
main()Сработало!
Я услышал величественные пищащие звуки, воспроизводимые моим собственным кодом.
Далее я занялся делением notes на отдельные треки…(что оказалось довольно легко благодаря продолжительным промежуткам тишины между ними).
Теперь можно было переходить к созданию «The Player (ТМ)».
Шаг 1. Цель
Все это не будет столь весело, если не воссоздать оригинальную среду – то есть медленные машины, дрянные спикеры и т.д.
Я решил делать все по максимуму (если у вас возникнет вопрос «Зачем?», то вы читаете не ту статью). Моя цель – создать автономный плеер на базе ATtiny85.

Это значит:
- 512 байт ОЗУ;
- … и 8Кб флэш-памяти.
И все: всего 8.5Кб пространства. Еще меньше, чем на моем ZX Spectrum
Вы, молодые люди со своими гигабайтами, нам не нужны! :)
Шаг 2. Вместись, пожалуйста, вместись
Очевидно, что не удастся втиснуть аудио данные в 512 байтов ОЗУ. Одни только ноты без задержек в виде 16-битных значений занимают больше 2.6Кб.
$ head frequencies_0.data
989
784
658
494
392
329
165
65535
329
65535
$ wc -l frequencies_*
1360 frequencies_0.data
211 frequencies_1.data
706 frequencies_2.data
376 frequencies_3.data
2653 totalМдаа…
Начнем с перемещения данных в область флэш-памяти микроконтроллера – туда же, где будет размещаться наш код.
Небольшой фрагмент Python преобразует ноты и задержки в аккуратные const-массивы Си…
const unsigned short frequencies[] PROGMEM = {
989,
784,
...
};
… в сопровождении PROGMEM, сообщающей кросс-компилятору, что их нужно поместить в область флэш-памяти.
Компилируем, подключаемся…иииии…Нет.
Тут без вариантов.
Время задуматься о сжатии.
Шаг 3. Алгоритм Хаффмана
Я проработал инженером ПО уже более 30 лет, и кастомное сжатие для меня не ново. На деле мое понимание указателей сформировалось еще при написании на Си кода сжатия во втором семестре обучения 1990 года. Тогда я реализовывал чудесное, на мой 18-летний взгляд, кодирование Хаффмана.
Вы можете спросить: «А что такое кодирование Хаффмана?» Подробности находятся под предложенной выше ссылкой, но сам его смысл очень прост:
- Если мы обозначим битами наиболее частые данные;
- и с помощью дополнительных битов обозначим менее частые данные…
… то в целом нам потребуется гораздо меньше битов.
К примеру, в данном случае нужно сжать 16-битные значения частоты. Предположим, что в музыкальных данных очень часто встречается частота 989Гц. Тогда можно представить ее значения как один бит: 0. Все остальные частоты при этом будут представлены с дополнительным префиксом 1 в начале, но если у нас в данных достаточно вхождений частоты 989Гц, то мы сожмем каждое из них до всего одного бита – то есть до 1/16 его исходного размера. Таким образом, мы существенно сэкономим пространство (более, чем достаточно, чтобы компенсировать «потери» из-за дополнения значений остальных частот).
Как же создать оптимальные коды для входных данных? Без особых сложностей с помощью алгоритма на основе кучи я смог переписать код с нуля, как делал это 30 лет назад – только теперь я был мудрее. В Google мне не удалось найти алгоритм Хаффмана для вложенных пространств, но я без проблем могу переиспользовать код в более высокоуровневых языках, чтобы сжать данные треков в коды Хаффмана, после чего просто самостоятельно написать на С/С++ декодер для воссоздания данных в реальном времени на борту ATtiny85.
После недолгих поисков в сети кода Python, реализующего алгоритм Хаффмана, я нашел этот фрагмент Rosetta. В Python возможность реализации кучи есть изначально, так что получилось весьма лаконично и понятно.
Хотя на деле как раз ясности коду не доставало. Поэтому я решил внести в него спецификации типов, что тут же упростило восприятие.
Сравните этот вариант…
def encode(symb2freq):
"""Алгоритм Хаффмана кодирует заданный словарь, сопоставляя символы и весами"""
heap = [[wt, [sym, ""]] for sym, wt in symb2freq.items()]
heapify(heap)
while len(heap) > 1:
lo = heappop(heap)
hi = heappop(heap)
for pair in lo[1:]:
pair[1] = '0' + pair[1]
for pair in hi[1:]:
pair[1] = '1' + pair[1]
heappush(heap, [lo[0] + hi[0]] + lo[1:] + hi[1:])
return sorted(heappop(heap)[1:], key=lambda p: (len(p[-1]), p))… с этим:
# Типы, используемые алгоритмом Хаффмана.
Symbol = int # Входные данные представлены в байтах
Weight = int # Мы подсчитываем их частоты с помощью счетчика
BinaryString = str # ...и кодируем в двоичную строку
HuffmanTable = List[Tuple[Symbol, BinaryString]] # здесь.
# Типы, необходимые в процессе кодирования
HeapEntry = Tuple[Weight, HuffmanTable]
Heap = List[HeapEntry]
# Создаем таблицу Хаффмана...
def make_huffman_table(
symbol_to_weight: Dict[Symbol, Weight]) -> HuffmanTable:
"""
Из словаря, где символы сопоставляются с весами, создаем таблицу Хаффмана.
Так как символы являются целыми числами, в результате получается таблица, состоящая из
(целого числа, используемой для этого числа двоичной строки).
"""
heap = [
(wt, [(sym, "")])
for sym, wt in symbol_to_weight.items()] # type: Heap
heapify(heap)
while len(heap) > 1:
lo_weight, lo_entries = heappop(heap)
hi_weight, hi_entries = heappop(heap)
new_lo_entries = [
(symbol, '0' + binary_string)
for symbol, binary_string in lo_entries]
new_hi_entries = [
(symbol, '1' + binary_string)
for symbol, binary_string in hi_entries]
heappush(
heap,
(lo_weight + hi_weight, new_lo_entries + new_hi_entries))
_, huffman_data = heappop(heap)
return sorted(huffman_data, key=lambda p: (p[0], len(p[-1])))Мне нравится код Python, действительно нравится.
Но должен сказать прямо: «спецификации типов в нем очень помогают. ПМСМ, это самое важное изменение в Python 3.
Комментарии тоже не повредят.
Выше видно, что я также изменил код, удалив мутации списков. Почему бы сразу не создать новые списки? В наше-то время это можно себе позволить. В итоге код будет «верно» типизирован. Если до этого список содержал два разных типа, то теперь в нем находятся кортежи, то есть пары элементов.
При этом мы также заработаем баллы качества за улучшение функционального стиля кода.
С целью довести его до совершенства, я продолжил доработку, пока код не прошел проверки Flake8, Pylint и Mypy. И для полной победы провел статический анализ.
В завершении я добавил самый простой тест – создал 5,000 входов данных и выполнил кодирование/декодирование, проверив правильность воссоздания кодом начальных значений.
Это быстро расширило степень покрытия до 100%.
def test_round_trips() -> None:
import random
TESTS = 5000
data = [
10 if random.randint(0, 10) < 7
else random.randint(0, 65536)
for i in range(TESTS)]
huffman_table, encoded_bitstream = encode(data)
decoded_data = decode(huffman_table, encoded_bitstream)
print("[-] Compression ratio: %5.2f%%n" % (
100.*len(encoded_bitstream) / (TESTS*16)))
assert data == decoded_dataОбратите внимание, что тест намеренно делает разброс значений асимметричным, так как набор совершенно случайных входных данных, где каждое значение аналогично любому другому, само собой, сжать не получится.
Вот теперь я смог действительно довериться декодеру Хаффмана.
На случай, если вы вдруг захотите поиграться с этим кодом Python, я поместил его в отдельный репозиторий GitHub – можете смело над ним изгаляться:)
Теперь я был готов применить всю мощь Хаффмана к извлеченным аудиоданным…
$ ./encode_huffman.py
[-] Reading frequencies_0.data
[-] Reading frequencies_1.data
[-] Reading frequencies_2.data
[-] Reading frequencies_3.data
[-] Creating Huffman table for all frequencies data...
[-] Huffman encoding for frequencies_0.data: 28.9%
[-] Huffman encoding for frequencies_1.data: 34.2%
[-] Huffman encoding for frequencies_2.data: 26.7%
[-] Huffman encoding for frequencies_3.data: 29.4%
[-] Reading delay_0.data
[-] Reading delay_1.data
[-] Reading delay_2.data
[-] Reading delay_3.data
[-] Creating Huffman table for all delay data...
[-] Huffman encoding for delay_0.data: 30.0%
[-] Huffman encoding for delay_1.data: 29.2%
[-] Huffman encoding for delay_2.data: 31.5%
[-] Huffman encoding for delay_3.data: 36.6%
Сокращение до ~30%! Победа...
Превосходно! Мы добились сокращения изначального объема до ~30%.
Затем я поместил сжатые двоичные строки в виде серии байтов также в const-массивы, сопровожденные PROGMEM…
… и кросс-компилятор сообщил, что все вместилось в 8Кб флеш.
Шаг 4. Кодирование (таблица Хаффмана)
Так, стоп.
Данные в кодировке Хаффмана ничего не значат без соответствующих таблиц. Их тоже нужно было сохранить.
Я попробовал…
…иии опять не хватило места.
Хмм…
Таблица Хаффмана содержит информацию о каждом входном символе (то есть каждом значении частоты) в следующем виде:
{ -1 /* тишина */, 0, 0 },
...
{
783 /* частота в Гц */, 3 /* длина в битах */,
0x80 /* первые 3 бита, то есть '100' */ },
{
989 /* частота в Гц */, 5 /* длина в битах */,
0x90 /* первые 5 бит, то есть '10010' */ },
...
Давайте применим метод брутфорс-я-идиот:
- Во-первых, вместо сохранения по 16 битов на частоту можно сохранить их дельты (в примере выше вместо сохранения 989 сохранить 989-783). При создании таблицы я ее упорядочил, поэтому дельты всегда вписываются в один байт. Это означает, что для каждой записи мы выигрываем по одному байту пространства.
- Теперь, длина в битах никогда не превышает 15. Значит, она вписывается в 4 бита – еще один выигрыш в полбайта на запись.
- Таким образом, я могу сгенерировать один массив байтов в следующем формате:
[8-bits-of-frequency-delta][4 bits of length][Huffman bits]
[8-bits-of-frequency-delta][4 bits of length][Huffman bits]
[8-bits-of-frequency-delta][4 bits of length][Huffman bits]
...Далее я занялся его кодировкой.
Вся разъясняемая мной логика написана на Python и генерирует данные таблицы Хаффмана в виде определений массивов Си.
Вам реально стоит к этому привыкнуть (имеется ввиду к генерации кода). Она дает невероятные возможности. Большинство людей вроде меня выясняют это в ходе собственных нелегких изысканий. Те же, кто поумнее и/или поудачливее, сначала встречают макрос Lisp либо читают книгу «Программист-прагматик».
«Официально» эта практика называется проектированием на основе моделей, хотя я здесь этим термином немного злоупотребляю. В нашем случае модель максимально примитивна – это аудиоданные. Но достаточно сказать, что базовый принцип здесь стар как сама наука автоматизации: если вы можете создавать что-либо автоматически, то должны так и делать. И это также касается кода.
В последние годы я много читал «Программист-прагматик». Эта книга дает много советов, которые я открывал ранее на собственном горьком опыте: генерация кода, не копипастить, не повторяться и пр.
Думаю, вам эта книга тоже может очень пригодиться.
Новый код упаковал таблицу достаточно плотно…
huffman_table_binary_string = ''
for idx, row in enumerate(huffman_table):
symbol, binary_string = row
assert len(binary_string) < 16
# Кодируем символ
if idx == 0:
v = 255 if symbol == -1 else symbol
else:
v = symbol-oldSym
assert 0 < v < 256
tv = bin(v)[2:]
while len(tv) < 8:
tv = '0' + tv
huffman_table_binary_string += tv
oldSym = symbol
# Кодируем длину
length_string = bin(len(binary_string))[2:]
while len(length_string) < 4:
length_string = '0' + length_string
huffman_table_binary_string += length_string
# В завершении добавляем код Хаффмана
huffman_table_binary_string += binary_string
fout.write(', '.join(getHex(huffman_table_binary_string)))… а кросс-компилятор сообщил о том, что и аудиоданные, и таблица Хоффмана теперь вместились!
В коде выше вы заметите:
- Вычисление дельты
(symbol - oldSym); - Инструкции
assert, проверяющие выполнение наших допущений (например, чтобы длина всегда вмещалась в 4 бита); - … а также создание 4-битовой строки с этой длинной, дополненной начальными нулями.
Обратите внимание еще вот на что: обычно нежелательно создавать в Python строки простым конкатенированием. Гораздо быстрее добавить их в список и в конце выполнить .join. Но нужно помнить – это генератор кода. Неважно, как быстро он выполняется, главное, чтобы не слишком медленно (в нашем случае все нормально – он справился со всеми 4-мя извлеченными мелодиями меньше, чем за секунду).
Хорошо! Пора переходить к написанию на Си декодера, который будет выполняться на микроконтроллере…
Шаг 5. Декодирование
Писать на Си – как кататься на велосипеде – никогда не разучишься:
#define GET_BITS(N, val)
do {
uint16_t cnt_bits = 0;
while (cnt_bits < N) {
val <<= 1;
if (current_huffman_mask & *p) {
val |= 1;
}
cnt_bits++;
current_huffman_mask >>= 1;
if (!current_huffman_mask) {
p++;
current_huffman_mask = 0x80;
}
}
} while(0)
const Huffman *p = pHuffmanTable;
current_huffman_mask = 0x80;
int16_t value = 0;
// Получаем первый символ (он вписывается в 8 бит)
GET_BITS(8, value);
if (value == 255)
value = -1;
while(p < pHuffmanTableEnd) {
// Для каждой записи в таблице Хаффмана...
uint16_t bitmask = 0x8000;
uint8_t cnt = 0;
// Сначала получаем 4 бита, указывающие длину...
GET_BITS(4, cnt);
uint8_t consumed_bits = cnt;
uint16_t code = 0;
// ...затем получаем биты длины...
GET_BITS(consumed_bits, code);
// Требуется битовая маска, чтобы сравнивать только интересующие нас биты
code <<= (16 - consumed_bits);
while(--cnt)
bitmask |= bitmask >> 1;
if (code == (bits & bitmask)) {
// Ура! Мы декодировали символ
fprintf(fp, "%dn", value == -1 ? 65535 : value);
fflush(fp);
loaded_bits -= consumed_bits;
total_bits -= consumed_bits;
p = pHuffmanTable;
break;
}
uint8_t delta = 0;
GET_BITS(8, delta);
// Создаем новый символ через прибавление дельты
value += delta;
}
if (!total_bits)
break;
Каждый входящий символ проходит через магию потока битов, попадая в таблицу Хаффмана. И каждый раз происходит декодирование этого символа (закодированного с помощью дельты, то есть value+=delta), считывание 4 битов длины, сообщающих, сколько всего последует битов и, наконец, считывание этих самых битов, которые сравниваются с «заголовком» битового потока.
Мы знаем, что у нас нет кодирующих последовательностей длиннее 15 бит, значит 16-битного code достаточно – поэтому используем двоичное И, чтобы замаскировать не интересующие нас биты, и выполняем сравнение с остатком: code == (bits & bitMask).
Если значения совпадают, значит символ успешно декодирован.
Этот код сначала тестировался на хосте (отсюда и fprintf): я использовал его для декодирования данных из сгенерированных Python массивов Си и проверял их на совпадение с оригинальными мелодиями.
Они совпали! Код Хорош (ТМ).
Пора записывать его на микроконтроллер…и подключать динамик!
Шаг 6. Подключение динамика
Если вы, как и я, любите ковыряться с электроникой, то наверняка много экспериментируете с микроконтроллерами. Одним из первых открытий обычно становится то, что эти крохотные создания (начиная с ATtiny и заканчивая ESP32) при попытке получить от них слишком большой ток начинают страдать провалами напряжения.
Проще говоря: да, можно легко сгенерировать на микроконтроллере частоту, активируя вывод GPIO в правильное время. Но если просто подцепить его к динамику в надежде, что тот заработает, то ничего не выйдет.
Предположим, что ваш спикер имеет сопротивление 8Ом. Если вы просто подключите его на микроконтроллере к выводу 5В, то будете ожидать на выходе 5000мВ/8Ом = 625мА. Что ж, могу лишь пожелать удачи.
Нет, динамиком нужно именно управлять. И да, можно взять готовую микросхему, например LM386, но разве это интересно?
Нет, и мы используем всего один транзистор. Просто, потому что можем.
Так пишут на форумах, значит должно сработать!
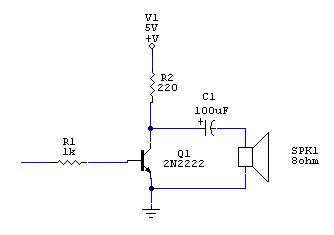
Настраиваем управление динамиком
Несмотря на то, что 30 лет назад это было частью моей технической программы, в области электроники мне доверять не стоит. Со скидкой на это могу сказать насчет схемы, что:
- Нам нельзя доводить транзистор до насыщения, так как звук получится искаженный.
- Поэтому мы выбираем умеренное значение в 1К – этот базовый ток удержит транзистор в более-менее линейной области.
- Нам также нельзя подавать на динамик постоянный ток, ведь мы не хотим его сжечь.
- Следовательно, нужен конденсатор. Для этой задачи вполне сгодится электролитический вариант на 100uF. У меня как раз такие есть.
- Наконец несмотря на то, что динамик мы подключаем к источнику питания, а не к выводу микроконтроллера, все равно нельзя подавать на него слишком большой ток. Значит, берем резистор 220Ом.
Все это лишь примерно, и для более точных расчетов нужно смотреть спецификации.
Но я ведь делаю это ради развлечения :)
Так что далее я перешел к очередному шагу: сборке комплекта на макетной плате и его тестированию с использованием BluePill…

Игрок один готов
Этот малыш обладает нехилыми возможностями – с его помощью я даже реализовал зум фракталов Мандельброта.
Ладно, он умеет рисовать, но сможет ли петь?
Для переключения вывода GPIO, управляющего базой транзистора на частотах аудиодорожек, я использовал конечный автомат:
// в основном цикле:
unsigned long currentMicros = micros();
int passedMicros = currentMicros-previousMicros;
switch(state) {
case Silence:
silenceMicrosRemaining -= passedMicros;
if (silenceMicrosRemaining < 0) {
updateState();
}
break;
case PlayingON:
onMicrosRemaining -= passedMicros;
if (onMicrosRemaining < 0) {
onMicrosRemaining = onMicros;
state = PlayingOFF;
digitalWrite(SPEAKER_PIN, LOW);
digitalWrite(LED_PIN, LOW);
}
break;
case PlayingOFF:
offMicrosRemaining -= passedMicros;
if (offMicrosRemaining < 0) {
offMicrosRemaining = offMicros;
if (!periodsRemaining) {
updateState();
} else {
periodsRemaining--;
state = PlayingON;
digitalWrite(SPEAKER_PIN, HIGH);
digitalWrite(LED_PIN, HIGH);
}
}
}
previousMicros = currentMicros;Заметьте, что здесь нет задержки. Код непрерывно мониторит время, проверяя сколько его прошло с момента последней проверки. Таким образом, он может адаптироваться под любую скорость работы микроконтроллера, а также выполнять другие задачи (например, проверять кнопку).
Его логика в данном случае проста: мы переключаем вывод ON/OFF, генерируя нужную частоту; делаем мы это в течение определенного количества периодов, чтобы получить задержку, которую повторно вычисляем каждый раз, когда нужно сгенерировать новую ноту:
void updateState()
{
int freq = decode_frequency();
int durationMS = decode_delay();
if (freq != -1) {
int volume = 60;
periodMicros = 1000000/((long)freq);
onMicros = periodMicros * volume/100;
offMicros = periodMicros * (100-volume)/100;
state = PlayingON;
onMicrosRemaining = onMicros;
offMicrosRemaining = offMicros;
periodsRemaining = ((long)durationMS)*1000L/periodMicros;
digitalWrite(SPEAKER_PIN, HIGH);
digitalWrite(LED_PIN, HIGH);
} else {
state = Silence;
silenceMicrosRemaining = ((long)durationMS)*1000L;
digitalWrite(SPEAKER_PIN, LOW);
digitalWrite(LED_PIN, LOW);
}
}
Далее выполняем make && make upload, и…

… Да! Он поет!
Я слышу чудесные тюны одной из величайших игр всех времен…прямо как 30 лет назад.
При этом светодиод подмигивает в момент перехода от ноты к задержке и обратно. Приятный бонус:)
Еще я сделал простую кнопку, позволяющую переключаться на следующую мелодию. В обычном состоянии она притянута к GND, но при ее нажатии вывод GPIO подтягивается вверх:
if (digitalRead(BUTTON_PIN) == HIGH) {
if (!buttonIsPressed) {
buttonIsPressed = true;
microsWhenButtonWasPressed = currentMicros;
}
} else {
if (buttonIsPressed && ((currentMicros-microsWhenButtonWasPressed)>100000L)) {
if (song == 0xFFFF) {
song = 0;
loadSong();
} else {
song++;
if (song >= sizeof(g_Melodies)/sizeof(g_Melodies[0]))
song = 0xFFFF;
else
loadSong();
}
buttonIsPressed = false;
}
}
Если вам интересно назначение первого if в блоке else, то он реализует самый простой вариант подавления дребезга кнопки – метод «just wait».
Затем выполняется перебор по сгенерированному Python глобальному массиву мелодий.
Шаг 7. Запуск ATtiny85
Далее я переключился на Makefile моего ATtiny85 и снова выполнил make && make upload. Для программирования ATtiny85 я использую Arduino UNO. Вообще, для упрощения процесса я собрал простенькую плату, которая в него «вставляется»:

Программатор ATtiny85
Сборка и запись кода прошли отлично.
Итак, я разместил микроконтроллер на ту же макетную плату, что и BluePill, подключил нужный GPIO к базе управляющего динамиком транзистора и…
О, нет…
Он играет…Но не успевает по времени! ATtiny слишком медленный.
Или, если быть точнее, мой код недостаточно хорош. Пока что.
Шаг 8. Возвращаемся к таблицам Хаффмана
И вот я снова смотрю в код.
Он действительно сохраняет таблицу Хаффмана очень компактно, но совершенно не учитывает то, что при декодировании нам приходится перебирать в таблице каждый символ в поиске нужного.
Это не путь Хаффмана. Помните, я упоминал о том, как на самом деле освоил принцип работы указателей в Си, реализуя кодирование Хаффмана? Тогда я создавал реальное дерево, в котором входящие 0 вели к левому потомку, а входящие 1 к правому, пока не достигался концевой узел, сообщавший о декодировании такого-то символа.
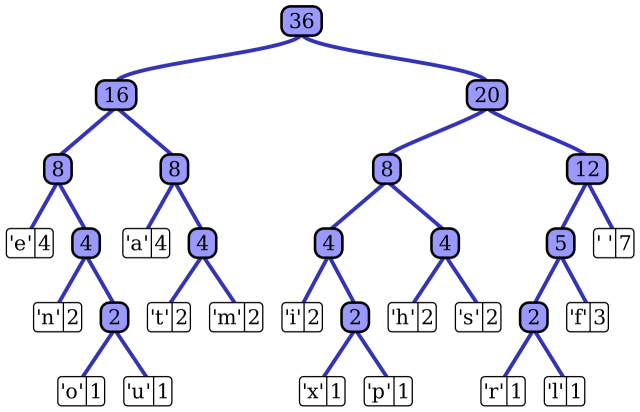
Дерево Хаффмана из Википедии
В плане времени выполнения такая схема оптимальна.
Здесь же я, наоборот, сосредоточился исключительно на оптимизации занимаемого пространства, заплатив за это временем O(N) (полным сканированием таблицы) для каждого входящего символа.
Хорошо – но использовать дерево не вариант. У нас просто нет под такую роскошь места – даже простейшая сериализация (сохранение левого потомка узла N в 2xN, а правого в 2xN+1) полностью исчерпает и без того крохотное пространство памяти.
Мне нужно каким-то образом втиснуть все и при этом добиться быстрого декодирования. Но как?
Хмм…
Подождите-ка.
Коды Хаффмана устроены так, что, если просматривать их бит за битом с самого начала, то они никогда не пересекуться. Иначе говоря, не существует двух символов, которые бы начинались с одинакового префикса.
Взгляните на дерево выше – мы обходим его сверху вниз, переходя влево или вправо в зависимости от встречаемых в битовой строке 0 и 1. Формируемое из этих битов число при достижении итогового символа получается уникальным – никакой другой символ такое иметь не может.
А теперь представьте, что помещаете все символы Хаффмана в таблицу, индексированную целочисленными значениями их двоичного строкового представления и содержащую в качестве значения сам символ (в нашем случае, частоту).
Если код Хаффмана, указывающий на ячейку, отсутствует, сохраняем ноль.
В итоге получится очень разреженная таблица, но декодирование при этом станет очень простым и быстрым:
bits <<= 1;
if (current_mask & *pCompressedData)
bits |= 1;
current_mask >>= 1;
total_bits--;
if (!current_mask) {
current_mask = 0x80;
pCompressedData++;
}
if (pHuffmanTable[bits]) {
fprintf(fp, "%dn", pHuffmanTable[bits]);
fflush(fp);
bits = 1;
...
}Чтобы все сработало, мне нужно лишь эффективно сохранить эту разреженную таблицу. А что может быть проще, чем изменить такой формат данных с нулями…
0, 739
1, 0
2, 0
3, 989
4, 0
5, 0
6, 0
7, 0
8, 1031
...… в такой – то есть «проигнорировать пустые ячейки и вывести только валидные записи»:
0, 739
3, 989
8, 1031Эта структура позволяет даже самому крохотному компьютерному быстро находить индекс. А вот и наш заключительный, быстрый декодер:
class HuffmanDecoder {
const uint8_t *_pCompressedData;
uint16_t _total_bits;
const Huffman *_pHuffmanTable;
uint8_t _loaded_bits;
uint8_t _current_mask;
uint16_t _bits;
public:
HuffmanDecoder() {}
void loadNewData(
const uint8_t *pCompressedData,
uint16_t total_bits,
const Huffman *pHuffmanTable)
{
_pCompressedData = pCompressedData;
_total_bits = total_bits;
_pHuffmanTable = pHuffmanTable;
_current_mask = 0x80;
_bits = 1;
}
int decode()
{
const Huffman *p = _pHuffmanTable;
uint16_t current_idx;
if (!_total_bits)
return 0x7FFF; // THE END
while(1) {
_bits <<= 1;
if (_current_mask & pgm_read_byte_near(_pCompressedData))
_bits |= 1;
_current_mask >>= 1;
_total_bits--;
if (!_current_mask) {
_current_mask = 0x80;
_pCompressedData++;
}
p = _pHuffmanTable;
while(1) {
current_idx = pgm_read_word_near(p);
if (_bits <= current_idx)
break; // Либо мы его находим, либо перескакиваем индекс
p += 2;
}
if (_bits == current_idx) {
int value = pgm_read_word_near(++p);
_bits = 1;
return value;
}
}
}
}
Заметьте, что считывание данных происходит из флэш-памяти через функции pgm_read_word_near и pgm_read_byte_near. В остальном же все просто. Мы продолжаем считывать биты, формируя индекс, который будем искать, затем заглядываем по ходу процесса в таблицу, проверяя индексы. Если происходит проскакивание, значит значения в таблице нет, и мы возвращаемся к считыванию.
Уточню: мы все равно выполняем сканирование «всей таблицы», но уже в другом ее виде, который не вынуждает нас возиться со смещением битов при поиске каждой записи. Наш код – его внутренний цикл – теперь намного проще. Я измерил размер объектного кода функции декодирования с помощью avr-nm --print-size -t d, выяснив, что размер нового декодера составляет 1/3 от прежнего.
Следовательно, выполняться на ATtiny85 он должен примерно в 3 раза быстрее, ведь на нем нет кэширования, которое бы этот процесс замедлило.
Кроме того, чем меньше код, тем больше остается флэш-памяти. Напомню, что там у нас хранятся не только мелодии, но и код.
Шаг 9. Автономный «The Player (TM)»
Пришло время тестировать — make && make upload, снимать ATtiny85 с программатора, подключать его к макетной плате и…
Новый код сработал безукоризненно. С первой попытки.
Значит, можно переходить к заключительному этапу – переносу всех компонентов на макетную плату.

The Player
А вот и видео результата. Запитанный от PowerBank проигрыватель в среднем потребляет меньше 10мА.
Надеюсь, что проект вам понравился, а, может, вы даже чему-то из него научились.
Вся база кода, использующая мой механизм Хаффмана в качестве подмодуля, находится здесь.
Всем удачи!
Автор: Дмитрий Брайт






