Restricted Boltzmann Machine — физика для рекомендательных систем

Привет, сегодня хочу предложить рассмотреть RBM модель для системы рекомендаций. Я думаю многие слышали о данном подходе для нейронных сетей, но именно в контексте рекомендательных систем информации на русском языке мало, хотя подход очень популярен. Здесь я сконцентрируюсь на математике, в свою очередь подсмотреть реализацию вы можете в репозитории recommenders Microsoft (https://github.com/microsoft/recommenders).

RBM — это модель генеративной нейронной сети, которая обычно используется для обучения без учителя. Основная задача RBM – изучить совместное распределение вероятностей , где – видимые единицы, а – скрытые. Скрытые единицы представляют собой скрытые переменные, в то время как видимые единицы ограничены входными данными. Как только совместное распределение изучено, путем выборки из него создаются новые примеры.

Модель генерирует рейтинги для пары пользователь-объект, используя подход, основанный на совместной фильтрации. В то время как методы матричной факторизации изучают, как воспроизвести экземпляр матрицы сходства пользователей-объектов, RBM изучает лежащее в основе распределение вероятностей. Это дает несколько преимуществ:

• Обобщаемость: модель хорошо обобщается на новые примеры, если они не сильно различаются по вероятности;

• Стабильность во времени: если задача рекомендаций стационарна во времени, модель не нужно часто обучать, чтобы приспособиться к новым рейтингам / пользователям.

Стоит отметить, что данная модель ­– это неориентированная графическая модель, первоначально разработанная для изучения статистической механики илифизики магнитных систем. Статистическая механика обеспечивает вероятностное описание сложных систем, состоящих из огромного числа компонентов (обычно ∼10²³). Вместо того, чтобы смотреть на конкретный экземпляр системы, цель статической механики описать их типичное поведение. Этот подход оказался успешным для описания газов, жидкостей, сложных материалов например,полупроводников и даже знаменитого бозона Хиггса! Разработанный для обработки и организации больших объемов данных, алгоритм идеально подходит в современных алгоритмах обучения. В контексте рекомендательных систем идея состоит в том, чтобы изучить типичное поведение пользователя, а не конкретные примеры.

Основной величиной каждой модели статической механики является распределение Больцмана – это можно рассматривать как наименее смещенное распределение вероятностей на данном вероятностном пространствеи может быть получено с использованием принципа максимальной энтропии на пространстве распределений над. Его типичная форма:

где,– нормировочная константа, известная как статистическая сумма,– параметр шума с единицами обратной энергии; – гамильтониан или функция энергии системы.

По этой причине этот класс моделей в информатике также известен как энергетический. В физике— это обратная температура системы в единицах постоянной Больцмана, но здесь мы фактически изменим масштаб внутри, так что теперь это натуральное число.описывает поведение двух наборов стохастических векторов, обычно называемых и Первые составляют вход и выход алгоритма, а скрытые единицы — это скрытые факторы, которые мы хотим изучить. Эта структура приводит к следующей топологии нейронной сети:

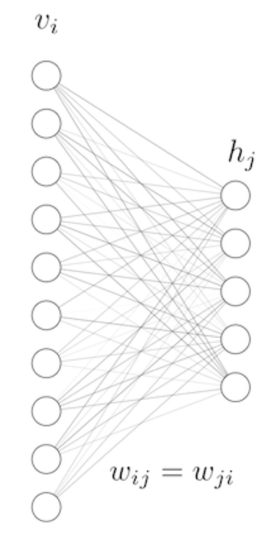
Теперь ближе к алгоритму. Входные данные выборки, которая используется разработчиком, состоят из оценок от 1 до 5. Таким образом, мы будем рассматривать дискретное конфигурационное пространство видимых переменных, каждая из которых принимает значения в конечном множестве . Глобальная конфигурация системы определяется следующим образом: и назначается 0 для объекта без рейтинга. В добавок также указываются скрытые блоки, которые мы принимаем в качестве случайных двоичных величин , обозначающих, активен конкретный блок или нет, и . Скрытые блоки могут описывать скрытые атрибуты объекта, дляфильмов−жанр,длястатей−областьисследованияит.д.. Минимальная модель такой системы определяется следующим гамильтонианом:

Первый член — это «термин взаимодействия», фиксирующий корреляции между видимыми и скрытыми единицами, в то время как два других члена являются «потенциальными терминами», принимая во внимание предвзятость единиц. Корреляционная матрица и два смещения и являются параметрами обучения, которые должны быть зафиксированы путем минимизации правильно определенной функции стоимости. При этом нельзя напрямую минимизировать функцию ошибок между прогнозируемыми и оригинальными данными. Как и в любой задаче статической механики, правильной величиной, которую нужно минимизировать, является свободная энергия (при этом в нашем случае ).

На языке теории вероятностей указанная выше величинаявляется кумулянтной производящей функцией. Одним из способов оценки свободной энергии является использование алгоритма выборки Монте-Карло с цепью Маркова, но здесь мы будем использовать вместо этого приближенный метод, называемый контрастной дивергенцией, основанный на выборке Гиббса. Его преимущество, в том, что он быстрее Монте-Карло. Как только кандидатбыл найден, мы фиксируем параметры обучения, минимизируя .

Рассмотрим модель более подробно. Вместо выборки непосредственно из совместного распределения вероятностей можно оценить условные распределения:

где второе равенство следует из того, что модель неориентирована или физически находится в равновесии. Выборка Гиббса по существу состоит из двух этапов, называемых положительной и отрицательной фазами.

Позитивная фаза начинается с фиксации видимых блоков в данных и определении , то есть определение вероятности того, что j-й скрытый блок активен для всего входного вектора. На практике производящую функцию удобно оценивать как:

Взяв градиенты по смещению, получим:

где , и логистическая функция идентифицируется как Собственно используется, чтобы выбрать значение .

В свою очередь негативная фаза включает использование выборочного значения скрытых единиц, чтобы определить , где . Это дается полиномиальным выражением:

где – статистическая сумма, вычисленная по результатам . Далее, выбираются значения из приведенного выше распределения. Разумеется, что эти новые не обязательно являются теми, которые мы использовали в качестве входных данных, по крайней мере, не в начале обучения. Вышеупомянутые шаги повторяются 𝑘 раз, причем 𝑘 обычно увеличивается во время тренировки в соответствии с заданным значением.

В конце каждой k-шаговой выборки Гиббса расчитывается разница между начальной свободной энергией при 𝑘 = 1 и заданном v и энергией после k-шагов и обновляются параметры обучения , , , путем дифференцирования .

Этот процесс повторяется для каждой обучающей эпохи, до тех пор, пока , то есть изученное распределение точно воспроизводит эмпирическое. В этом смысле служит как входом, так и выходом модели. Поскольку содержит информацию о том, как соотносятся оценки пользователей, мы можем использовать эту информацию для создания рейтингов для неоцененных объектов путем выборки из изученного предельного распределения:

На этом вообщем-то и все! Как упоминалось выше, реализацию можно посмотреть у Microsoft. Она достаточно хорошо задокументирована и предоставляет простые примеры с использованием RBM.

Исследуйте и развивайтесь! ​