Все мы знакомы из школьной программы с построениями при помощи циркуля и линейки. А что будет, если вдруг циркуль затеряется? Можно ли при помощи одной линейки строить ещё что-то нетривиальное? Предлагаю вашему вниманию задачу, решение которой принесло мне немало приятных часов. Задача со звёздочкой, поэтому не расстраивайтесь, если сходу решение не найдёте. Хотя один мой знакомый справился за пять минут, думаю, что это скорее исключение из правил.
Итак, на плоскости есть отрезок, который мы бы хотели продолжить. Казалось бы, выбрать две точки на отрезке, приложить линейку и прочертить прямую. Но вот незадача: как раз на пути этой прямой посажено жирное пятно кетчупа, а мы линейку пачкать не хотим. Нужно продолжить изначальную прямую за пятном, не прикасаясь к нему линейкой.
Напоминаю, циркуля нет, остаётся только неградуированная линейка, с помощью которой можно только проводить прямую через выбранные две точки, больше ничего. Это настоящая задача без подколок. Складывать листочки, использовать вторую сторону линейки для откладывания параллельных линий, а также хитрить другими подобными способами не требуется.
Update: Поскольку в комментариях задачу расщёлкали как орех, публикую два моих решения. Подглядывать в ответы, не попытавшись решить задачу самостоятельно, неспортивно :)
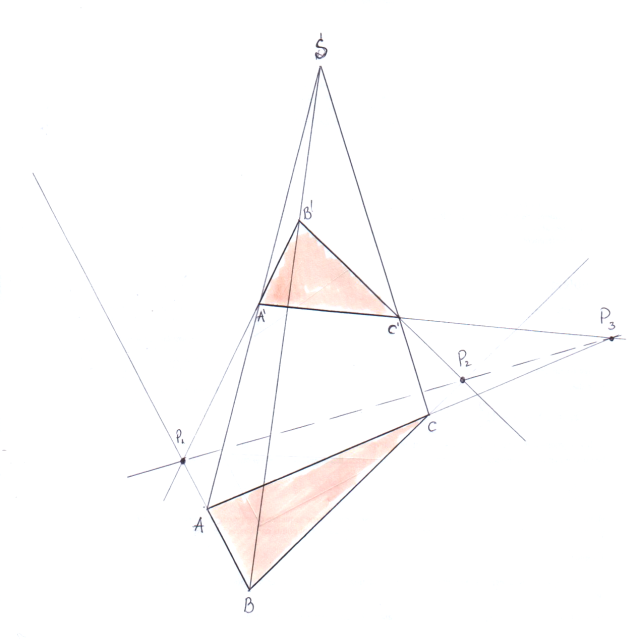
Прямые AB и A'B' пересекаются в точке P1, поскольку лежат в одной и той же плоскости (грань тетраэдра ABS). Аналогично P2 — точка пересечения прямых BC и B'C', и P3 — пересечение прямых AC и A'C'.
При этом P1, P2 и P3 лежат на одной прямой, поскольку принадлежат одновременно плоскости ABC и плоскости A'B'C', а пересечение двух плоскостей — это прямая.
То есть, произвольно взяв две точки P1 и P2 на нашем отрезке, мы можем построить P3, лежащую на той же прямой, но с другой стороны пятна. Повторив построение ещё раз, получим вторую точку, и задача решена. На всякий случай, это применение теоремы Дезарга
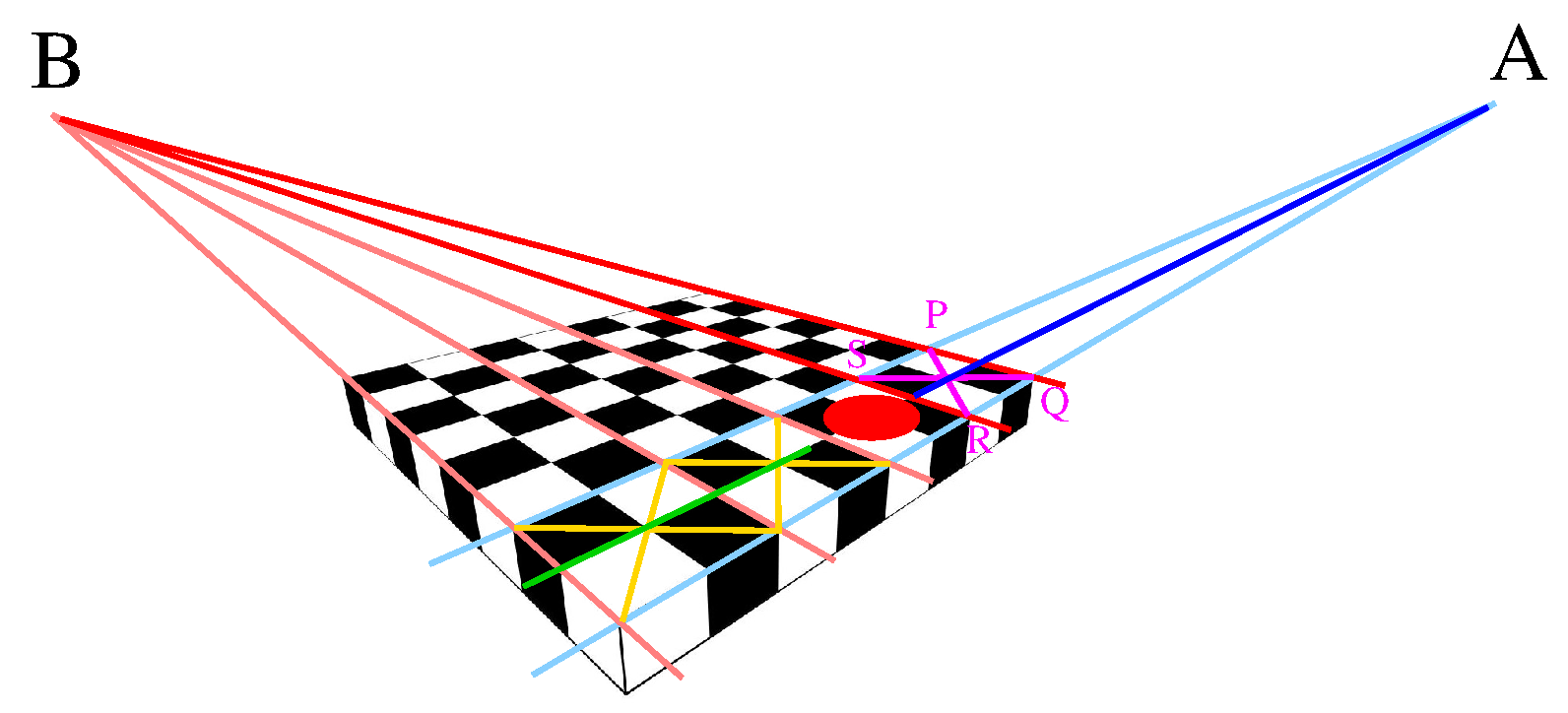
Наша прямая — синяя, эллипс — пятно кетчупа. Основная идея — нарисовать проекцию 3д плоскости, замощённой одинаковыми квадратиками кафеля. Точки A и B — это так называемые точки схода, то есть, точки, в которых пересекаются параллельные (в 3д) прямые, образующие границы кафельных плиток.
1. Проведём две произвольных фиолетовых прямых таким образом, чтобы точка их пересечения лежала на нашей синей прямой.
2. Выберем произвольную точку A на нашей синей прямой, и произвольно же проведём две голубых прямых.
3. Пересечение фиолетовых и голубых прямых даст четыре точки P, Q, R и S, которые являются углами главной кафельной плитки, от которой мы и будем плясать.
4. Нарисуем красные прямые QP и RS, и обозначим точку их пересечения как B, это будет вторая точка схода.
5. Ну а дальше дело техники: произвольно чертим три розовые прямые, получим ещё две плитки кафеля. Ищем их центры, начертив два жёлтых креста, и дело сделано.
Я даже анимацию нарисовал :)

Автор: haqreu






