Я преподаю курс экспериментальной оптики в одном из российских университетов. Складывается ощущение, что развитие вычислительной техники и программного обеспечения не оказывает влияния на ожидаемый прогресс в удобстве проведения измерений и качестве представления результатов лабораторных работ. Думаю, причина состоит в том, что офисные приложения для работы с электронными таблицами воспринимаются студентами как единственный подходящий инструмент для решения подобных задач. Чтобы развеять это сверхпопулярное заблуждение, я на простом примере расскажу об использовании пакета gnuplot.
Установка gnuplot
Gnuplot – высокоуровневый язык команд и сценариев, предназначенный для построения графиков математических функций и работы с данными, активно развивающийся с 1986 года. Исходный код gnuplot защищён авторским правом, но распространяется как свободное программное обеспечение и способен работать на Linux, OS/2, MS Windows, OSX, VMS и многих других платформах. Для установки gnuplot на компьютер с MS Windows наиболее удачным решением будет обратиться к официальному сайту gnuplot.info, перейти по ссылке «Download» и загрузить актуальную версию с ресурса sourceforge.net. Размер скачиваемого файла – около 30 Мб, после установки пакет занимает примерно 100 Мб дискового пространства.
Установщик задаст несколько простых вопросов о конфигурации (на английском языке), одно из окошек будет называться «Select Additional Tasks», в нем я рекомендую выбрать тип терминала wxt, а также поставить галочку в последнем пункте «Add application directory to your PATH environment variable». После установки в меню запуска программ появятся два новых пункта, кажется они называются «gnuplot» и «gnuplot console version». Если выбрать второй вариант, появится черное окно с командной строкой, как показано на рисунке:
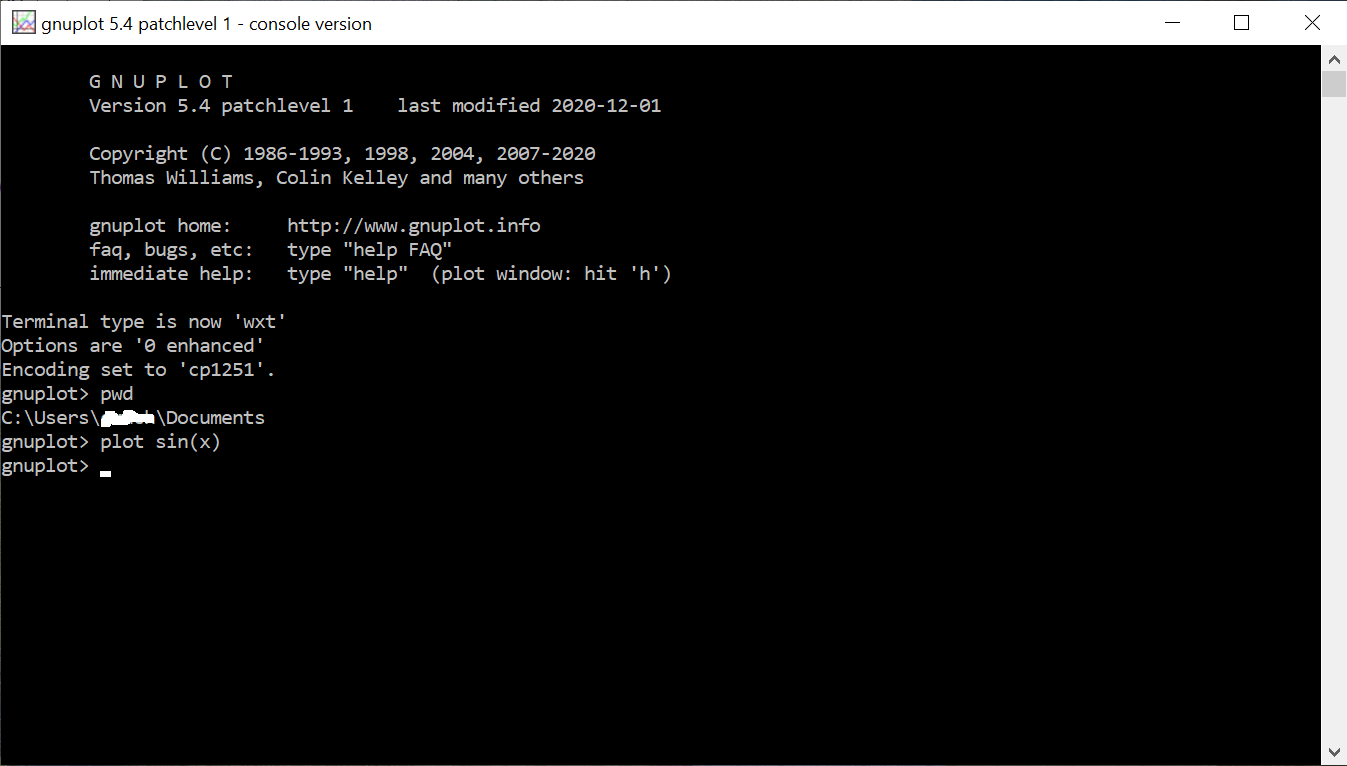
Если ввести командуpwd, вы увидите директорию, в которой запускается gnuplot. Команда plot sin(x)откроет графический терминал wxt и нарисует в нем график функции 
.
Если запускать просто gnuplot (не консоль), окно для ввода команд будет белое с черным текстом, при этом в нем будет отображатся верхнее меню с многочисленными командами. В gnuplot есть команда help для быстрого получения справки по любой из команд. Для облегчения работы с gnuplot пользователям MS Windows настоятельно рекомендую обзавестись нормальным текстовым редактором (я не очень в курсе текущей ситуации с Notepad).
Эксперимент
В качестве примера для настоящей заметки выберем простой опыт, относящийся к теме «поляризация света». Пусть у нас есть направленный источник линейно-поляризованного света, луч от которого проходит через линейный поляризатор и попадает на фотодетектор.
Измеряем напряжение на фотодетекторе, которое пропорционально мощности прошедшего через поляризатор излучения. Поляризатор представляет из себя тонкую пластинку, плоскость которой перпендикулярна лучу света. Поляризатор установлен в оправу, позволяющую вращать его вокруг направления луча, изменяя угол между плоскостью поляризации света и оптической осью поляризатора. Угол поворота оси поляризатора считывается со шкалы на оправе.
Теоретическая зависимость измеряемого напряжения 
от угла поворота поляризатора 
описывается законом Малюса:
где 
– угол межу плоскостью поляризации света и оптической осью поляризатора.
Моделирование
Применим gnuplot для моделирования возможных результатов эксперимента, в котором измеряется зависимость 
от угла поворота 
. Стоит отметить, что в реальных экспериментах моделирование изучаемого явления широко используется для создания и тестирования средств анализа результатов измерений. Отличие наблюдаемых величин от модельных данных заставляет исследователей проверять и совершенствовать модель, добавляя в нее уже известные науке эффекты. Ситуация, в которой результаты эксперимента невозможно описать известными явлениями называется открытием. Итак, создадим текстовый файл model.gpl со сценарием из gnuplot-команд и комментариев к ним:
reset # сбрасываем все ранее определенные переменные среды gnuplot
set angles degrees # используем градусы как единицу измерения углов
set xrange [0:350] # диапазон изменения угла поворота поляризатора
set samples 36 # число точек для вычисления значений функции
set format x "%5.1f" # формат вывода значения угла
set format y "%5.3f" # формат вывода величины напряжения
# Применим преобразование Бокса-Мюллера для моделирования 'ошибки'
# измерения угла, которая описывается нормальным распределением
# с нулевым средним и дисперсией D. Воспользуемся имеющимся в
# gnuplot генератором псевдо-случайных чисел, функцией rand(x):
err(D) = D * cos(360*rand(0))*sqrt(-2*log(rand(0)))
# Создадим функцию для описания закон Малюса:
U(x) = Uo * cos(x + err(D) - To)**2 + B
Uo = 0.65 # параметр Uo
To = 71. # параметр θo
B = 0.02 # напряжение на фотодетекторе при выключенном источнике света
D = 1.0 # ошибка считывания значения угла со шкалы на оправе
set table "exp.dat" # имя текстового файла для вывода результатов
plot U(x) # записываем результаты в файл
unset table # закрываем файлВ окне gnuplot набираем командуload 'model.gpl'.Подразумевается, что созданный нами файл находится в рабочей директории, в противном случае директорию можно сменить, введя команду cd 'your_path'. В результате выполнения скрипта мы получим текстовый файл cрезультатами моделированияexp.dat, который выглядит примерно так:
# Curve 0 of 1, 36 points
# Curve title: "U(x)"
# x y type
0.0 0.089 i
10.0 0.176 i
20.0 0.283 i
30.0 0.395 i
40.0 0.505 i
50.0 0.595 i
60.0 0.643 i
...Анализ данных
Начнем обработку данных с построения графика результатов моделирования (или измерений). Также используем метод наименьших квадратов для сравнения полученных результатов с теорией. Редуцированное значение взвешенного параметра хи-квадрат определяется так:
-
называется числом степеней свободы алгоритма поиска минимального значения 
и определяется как число измерений (точек на графике) минус количество свободных параметров функции 
,
-
– точки на оси x, в которых проведены измерения, -
– результат измерения в точке 
, -
– значение теоретической функции в точке 
, -
– среднеквадратическое отклонение измеренного значения величины 
от ее среднего значения 
.
В gnuplot отношение 
из последней формулы обозначается как WSSR / NDF, что является аббревиатурой от фраз «Weighted Sum of Squared Residuals» и «Number of Degrees of Freedom».
Рассматриваемый здесь пример лабораторной работы является частным случаем обширного класса задач, в которых есть набор данных измерений/моделирования и теоретическая функция, которая «должна» описывать изучаемое явление. Для проверки соответствия между теорией и экспериментом мы будем варьировать свободные параметры функции так, чтобы минимизировать величину 
. Для этого в gnuplot есть команда fit, изпользующая алгоритм Левенберга — Марквардта. На русский язык фраза «fit function to data» переводится как «подогнать функцию к данным».
Создадим текстовый файлlook.gpl со сценарием для gnuplot.
reset
set angles degrees
f(x) = Uo * cos(x-To)**2 + B # определение теоретической функции
Uo = 0.6 # параметр Uo
To = 10 # параметр To
B = 0.05 # параметр B
set fit nolog # отмена опции записи логов процесса подгонки в файл
# Запускаем алгоритм поиска минимума хи-квадрат, используя 1 колонку файла
# "exp.dat" в качестве X[i], а вторую - в качестве Y[i]. При поиске минимума
# алгоритм варьирует значения свободных параметров Uo, B, To
fit f(x) "exp.dat" using 1:2 via Uo, To, B
# Среднее квадратичное отклонение эксперимента и теории в милливольтах
L = sprintf("Закон Малюса: {/Symbol s} = %.2f [мВ]", 1000*FIT_STDFIT)
# Найденное значение угла поворота оси и оценка его точности
T = sprintf("Поворот оси поляроида {/Symbol q_0} = %.2f° ± %.2f°", To, To_err)
set title T # Название для получившегося графика
set grid # Указание рисовать сетку на графике
set key box width -14 # прямоугольник для отображения подписей к графикам
set xlabel 'угол поворота поляризатора {/Symbol q} [ ° ]'
set ylabel 'напряжение на фотоприёмнике U [ В ]'
set yrange [0:0.8] # диапазон графика по вертикальной оси
set terminal png size 800, 600 # выбираем тип терминала - png файл
set out 'look.png' # имя файла для записи графика
# Рисуем функцию и точки из файла:
plot f(x) with line title L ls 3 lw 2,
"exp.dat" u 1:2 title 'эксперимент' with points ls 7 ps 1.5
set out # закрываем файлСимвол «» используется в сценариях для переноса длинных строк и должень быть последним символом в своей строке. В окне gnuplot вводим команду load 'look.gpl', в результате выполнения которой у нас появится файл look.png с построенными графиками данных и теоретической функции:
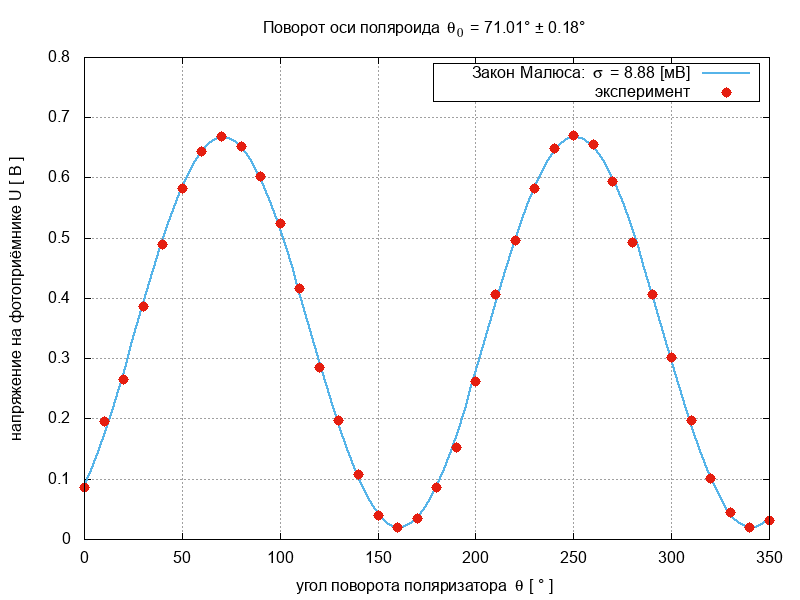
Итак, мы видим, что «на глазок» данные хорошо совпадают с теорией. Нам даже удалось правильно измерить угол 
с точностью 0.2 градуса. Однако, мы имеем среднеквадратическое отклонение теории от моделирования 
9 милливольт. Что бы это могло означать?
Если посмотреть на использование команды fit (строка №11 в файле look.gpl), можно заметить, что мы не передаём процедуре подгонки никаких данных об ошибках измерений, т. е. алгоритм ничего «не знает» о величинах
считаются равными безразмерной единице и мы получаем невзвешенное значение редуцированного параметра хи-квадрат, квадратный корень из которого является размерной величиной, описывающей среднеквадратическое отклонение функции от экспериментальных точек – те самые 8.88 милливольт, приведенные на графике.
Если в процессе измерений текущее наблюдаемое значение напряжения в каждой точке ведет себя достаточно стабильно, можно предположить, что отличие теории и эксперимента может быть связано с неточностью отсчета угла по шкале оправы с вращающимся поляризатором. Чтобы преобразовать ошибки отсчета угла в эквивалентные ошибки измерения напряжения, продифференцируем функцию 
и назовем получившуюся функцию 
:
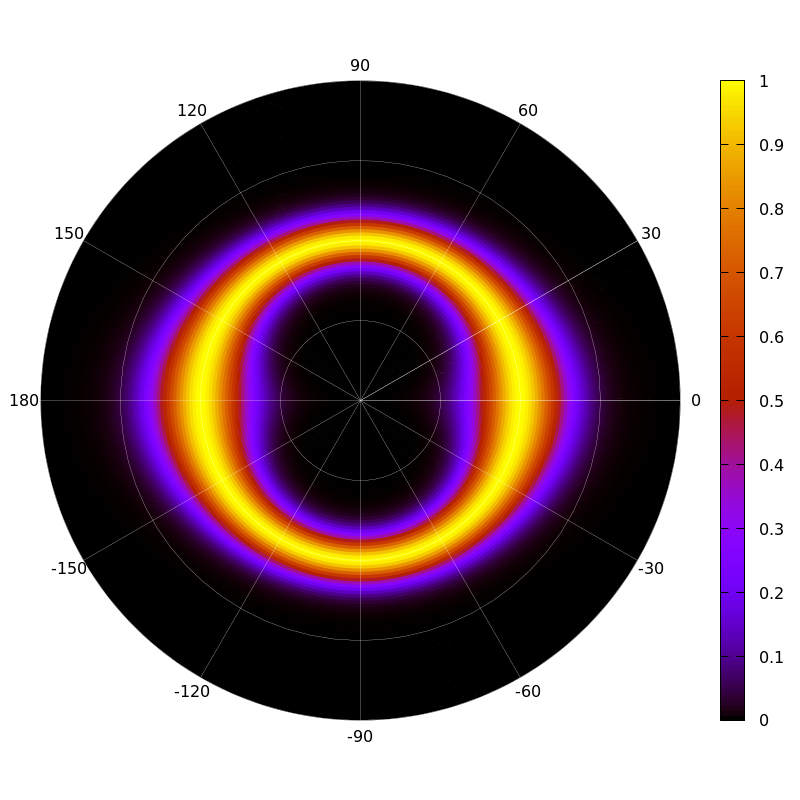
В нашем моделировании (см. файлmodel.gplв начале этого текста) мы «учли» погрешность измерения угла, добавив его к закону Малюса как случайную величину с нормальным распределением и среднеквадратическим разбросом в 1 градус. Чтобы учесть погрешности измерений, создадим усовершенствованный скрипт для обработки данных. Заодно, нарисуем графики в полярных координатах (удобных для визуализации поляризационных явлений), а также сохраним картинку в формате pdf.
reset
set angles degrees
f(x) = Uo * cos(x-To)**2 + B # определение теоретической функции
v(x) = Uo * sin(2*(To-x))*pi/180 # производная f(x)
Uo = 0.6 # параметр Uo
To = 10 # параметр To
B = 0.05 # параметр B
dT = 1.0 # ошибка измерения угла
set fit nolog
# Запускаем алгоритм поиска минимума (не-взвешенный хи-квадрат)
fit f(x) "exp.dat" using 1:2 via Uo, To, B
# Запускаем алгоритм поиска минимума (взвешенный хи-квадрат)
fit f(x) "exp.dat" using 1:2:(dT*v($1)) via Uo, To, B
L = sprintf("Теория: {/Symbol c^2}/NDF = %.1f/%2dn
Вероятность: %.2f %", FIT_WSSR, FIT_NDF, 100*FIT_P)
T = sprintf("Поворот оси поляроида {/Symbol q_0} = %.2f° ± %.2f°", To, To_err)
set title T # Название для получившегося графика
set key box left opaque width -12 spacing 2
unset border # не рисовать рамку
unset xtics # не показывать ось x
unset ytics # не показывать ось y
set polar # рисуем графики в полярных координатах
set grid polar linetype 2 lc rgb 'black' lw 0.25 dashtype 2
set rtics 0.1 format '%.1f'
unset raxis
Umax = 0.76 # максимальное значение напряжения
set rrange [0:Umax]
set rlabel 'U_{ФД} [В]'
set trange[0:360]
set for [i=0:330:30] label at first Umax*cos(i),
first Rmax*sin(i) center sprintf('%d°', i)
set terminal pdf background rgb '0xFFFFF0' size 5, 5 # тип терминала - pdf файл
set out 'closelook.pdf' # имя файла для записи графика
plot f(t) with line title L ls 3 lw 2,
"exp.dat" u 1:2:(dT*v($1)) title 'эксперимент' with err ls 7 ps 0.5
set out # закрываем файлСледующее изображение - скриншот получившегося файла closelook.pdf.
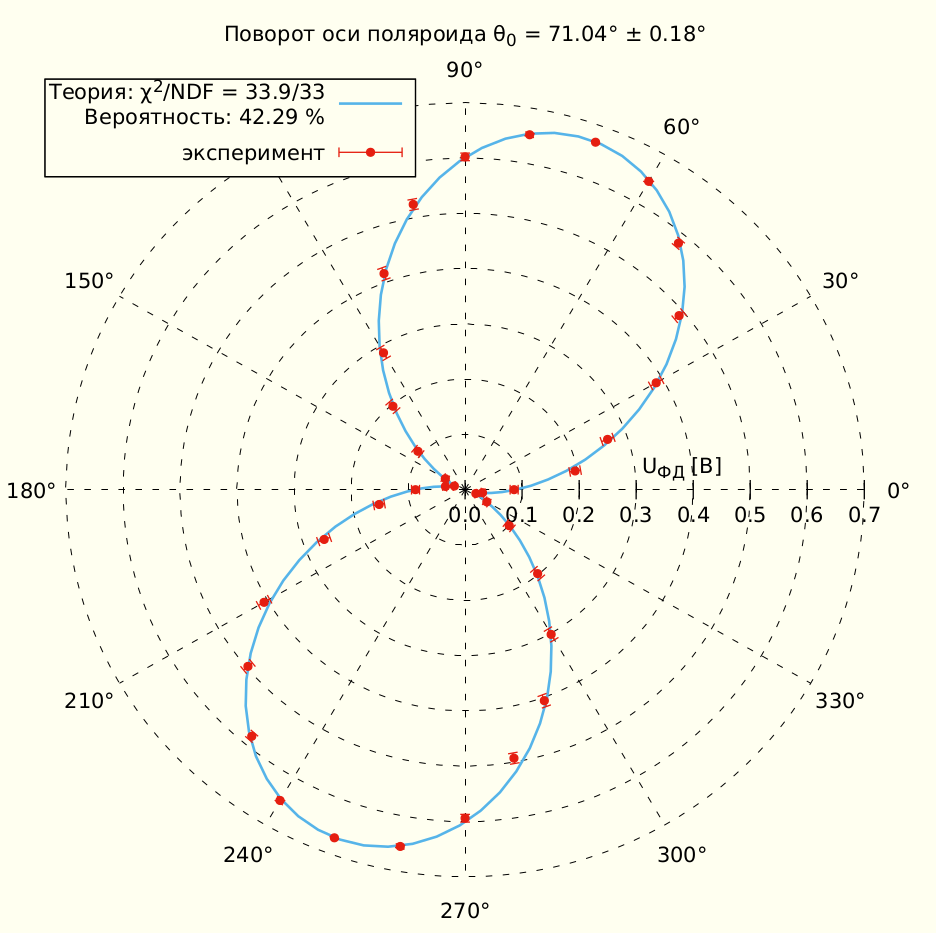
В результате применения алгоритма подгонки мы получили редуцированное значение взвешенного параметра хи-квадрат 
. Используя распределение хи-квадрат с соответствующим числом степеней свободы мы получаем значение вероятности (p-value) получения наблюдаемого результата в предположении, что исходная теоретическая гипотеза верна. В нашем случае эта вероятность довольно высока - 42%.
Заключение
Изучение пакета gnuplot, как и многих других инструментов, целесообразно начинать на примере решения какой-нибудь простой задачи. Существование готовых сценариев позволяет в дальнейшем легко адаптировать и видоизменять их под свои нужды. Открытость и мультиплатформенность программы и языка сценариев обеспечивает легкий обмен знаниями, данными, навыками и результатами работы.
Автор: daifu
