Введение
Криптоанализ — наука о том, как расшифровывать зашифрованную информацию, не имея в распоряжении ключа для расшифровки. Криптоанализом так же называется сам процесс дешифровки.
Чаще всего под криптоанализом понимается выяснение ключа шифрования, так как имея ключ криптоаналитик может расшифровать любое сообщение. Однако криптоанализ может заключаться и в анализе криптосистемы, а не только зашифрованного ею открытого сообщения, и включает также методы выявления уязвимости зашифровывающих алгоритмов.
Статистический криптоанализ — это один из методов криптоанализа. Как и в любой задаче, связанной с математической статистикой, вводится понятие статистики — некоторой величины, которая вычисляется на основе выборки или, в случае криптоанализа, - на основе криптограммы. В идеальном случае статистика должна быть простой в вычислении и использовании, а так же не сильно меняться от сообщения к сообщению, если эти сообщения зашифрованы одним и тем же ключом.
Цель статистического криптоанализа — расшифровать конечное сообщение, используя вычисленную статистику. В этой статье представлен обзор нескольких методов статистического криптоанализа от самых простых, до используемых в современных взломах.
Частотный анализ
Простые шифры
Частотный анализ использует гипотезу о том, что символы или последовательности символов в тексте имеют некоторое вероятностное распределение, которое сохраняется при шифровании и дешифровании.
Этот метод один из самых простых и позволяет атаковать шифры простой замены, в которых символы в сообщении заменяются на другие согласно некоторому простому правилу соответствия.
Однако такой метод совершенно не работает, например, на шифрах перестановки. В них буквы или последовательности в сообщении просто меняются местами, но их количество всегда остается постоянным, как в анаграммах, поэтому ломаются все методы, основанные на вычислении частот появления символов.
Для полиалфавитных шифров — шифров, в которых циклически применяются простые шифры замены — подсчет символов так же не будет эффективен, поскольку для кодировки каждого символа используется разный алфавит. Число алфавитов и их распределение так же неизвестно.
Шифр Виженера
Один из наиболее известных примеров полиалфавитных шифров — шифр Виженера. Он довольно прост в понимании и построении, однако после его создания еще 300 лет не находилось способа взлома этого шифра.
Пусть исходный текст это: МИНДАЛЬВАНГОГ
-
Составляется таблица шифров Цезаря по числу букв в используемом алфавите. Так, в русском алфавите 33 буквы. Значит, таблица Виженера (квадрат Виженера) будет размером 33х33, каждая i-ая строчка в ней будет представлять собой алфавит, смещенный на i символов.
-
Выбирается ключевое слово. Например, МАСЛО. Символы в ключевом слове повторяются, пока длина не достигнет длины шифруемого текста: МАСЛОМАСЛОМАС.
-
Символы зашифрованного текста определяются по квадрату Виженера: столбец соответствует символу в исходном тексте, а строка — символу в ключе. Зашифрованное сообщение: ЩЙЯРПШЭФМЬРПХ.

Этот шифр действительно труднее взломать, однако выделяющиеся особенности у него все же есть. На выходе все же не получается добиться равномерного распределения символов (чего хотелось бы в идеале), а значит потенциальный злоумышленник может найти взаимосвязь между зашифрованным сообщением и ключом. Главная проблема в шифре Виженера — это повторение ключа.
Взлом этого шифра разбивается на два этапа:
-
Поиск длины ключа. Постепенно берутся различные образцы из текста: сначала сам текст, потом текст из каждой второй буквы, потом из каждой третьей и так далее. В некоторый момент можно будет отвергнуть гипотезу о равномерном распределении букв в таком тексте — тогда длина ключа считается найденной.
-
Взлом нескольких шифров Цезаря, которые уже легко взламываются.
Поиск длины ключа — самая нетривиальная здесь часть. Введем индекс совпадений сообщения m:
где n — количество символов в алфавите и
p_i — частота появления i-го символа в сообщении. Эмпирически были найдены индексы совпадений для текстов на разных языков. Оказывается, что индекс совпадений для абсолютно случайного текста гораздо ниже, чем для осмысленного текста. С помощью этой эвристики и находится длина ключа.
Другой вариант — применить критерий хи-квадрат для проверки гипотезы о распределении букв в сообщении. Тексты, получаемые выкидыванием некоторых символов, все равно остаются выборкой из соответствующего распределения. Тогда в критерии хи-квадрат вероятности появления символов можно выбрать используя частотные таблицы языка.
Статистические атаки насыщения
Не только простейшие шифры подвержены статистическим методам криптоанализа. Например, статистические атаки насыщения направлены на блочные шифры, которые в настоящее время широко использутся в криптографических протоколах. Проиллюстрировать принцип таких атак удобно на блочном шифре PRESENT.
PRESENT
PRESENT - блочный шифр на основе SP-сети с размером блока 64 бита, длиной ключа 80 или 128 бит и количеством раундов 32. Каждый раунд состоит в операции XOR с текущим ключом, далее происходит рассеивание — пропускание через S-блоки, а затем полученные блоки перемешиваются.
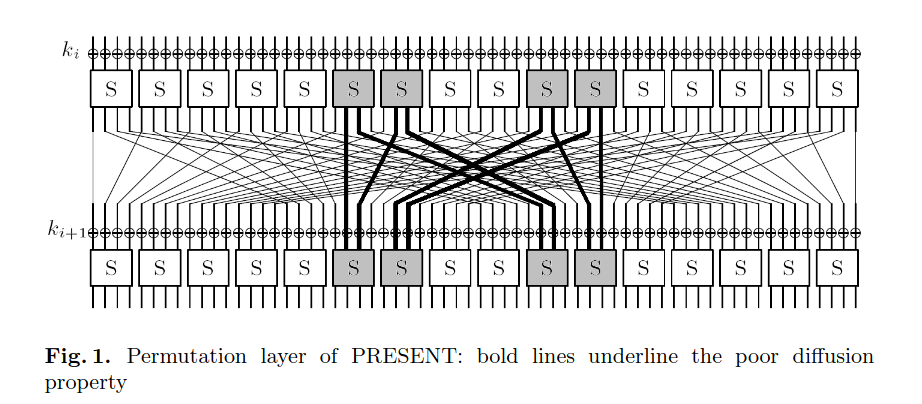
Предложенная атака основывается на уязвимости шифра на этапе перемешивания. Как показано на изображении, из входных битов 5, 6, 9 и 10 s-блоков половина соединений идет в те же самые биты. И это только один пример подобной слабости. Значит, фиксируя 16 битов на входе 5, 6, 9 и 10 s-блоков, можно определить 8 входных битов для этих блоков на следующем раунде.
Предполагая ключ на данном шаге, криптоаналитик может по выбранном распределению выбранных 8 битов на входе определить распределение тех же 8 битов на выходе. Проделав эту процедуру для каждого ключа, можно понять все возможные распределения выбранных 8 выходных битов 5, 6, 9 и 10 s-блоков на каждом слое, применяя алгоритм итеративно.
Когда криптоаналитик знает для каждого ключа, как распределены выбранные 8 битов на каждом слое, он может сравнить полученные распределения с теми, которые получаются в реальной системе. Для этого нужен доступ к алгоритму шифрования и большое количество текстов для шифрования. Из всех возможных ключей выбирается тот, который минимизирует расстояние между теоретическим и экспериментальным распределениями.
Линейный криптоанализ
Еще один метод взлома блочных шифров — линейный криптоанализ. Он является одним из самых распространенных подходов. Анализ основывается на построении соотношений между открытым текстом P, ключом K и зашифрованным сообщением C, а затем их использовании для нахождения ключа.
Соотношения в алгоритме — это уравнения следующего вида:
Вероятность выполнения этого соотношения для произвольно выбранных битов примерно равна 0.5. Цель линейного криптоанализа — найти такие наборы битов, что эта вероятность сильно отличается от 0.5 в одну или другую сторону. Вероятности подсчитываются путем полного перебора всех возможных значений входов для S-блока.
Ключ находится следующим образом:
Для каждого возможного набора битов ключа проверяется, на скольких парах текст-шифротекст выполняется найденное соотношением. Выбирается тот набор битов, для которого отклонение числа пар от половины всех пар наибольшее.
Линейный криптоанализ оказался очень мощным инструментом и может применять не только к блочным, но и к потоковым шифрам.
Заключение
В данной статье были рассмотрены наиболее известные техники статистического криптоанализа от простейшего частотного анализа до современных методов взлома блочных шифров. Сложность современных шифров все увеличивается, но статистика помогает найти в них уязвимости, поэтому методы криптоанализа все еще находят свое применение, несмотря на высказывания о его конце.
Автор: daha_kot







