Мифический носорогоединорог. MS TECH / PIXABAY
Обучение «менее чем с одной» попытки помогает модели идентифицировать больше объектов, чем количество примеров, на которых она тренировалась.
Как правило, машинное обучение требует множества примеров. Чтобы ИИ-модель научилась распознавать лошадь, вам потребуется показать ей тысячи изображений лошадей. Поэтому технология настолько вычислительно затратна и сильно отличается от человеческого обучения. Ребенку зачастую нужно увидеть всего несколько примеров объекта, или даже один, чтобы научиться распознавать его на всю жизнь.
На самом деле, детям иногда не нужны никакие примеры, чтобы идентифицировать что-нибудь. Покажите фотографии лошади и носорога, скажите, что единорог — это нечто среднее, и они узнают мифическое создание в книжке с картинками, как только увидят его в первый раз.

Ммм… Не совсем! MS TECH / PIXABAY
Теперь исследование из Университета Уотерлу в Онтарио предполагает, что ИИ-модели тоже могут это делать — процесс, который исследователи называют обучением «менее чем с одной» попытки. Иными словами, ИИ-модель может четко распознавать больше объектов, чем число примеров, на которых она тренировалась. Это может иметь решающее значение для области, которая становится все дороже и недоступнее по мере того, как растут используемые наборы данных.
Как работает обучение «менее чем с одной» попытки
Исследователи впервые продемонстрировали эту идею, экспериментируя с популярным набором данных для тренировки компьютерного зрения, известным как MNIST. MNIST содержит 60 000 изображений рукописных цифр от 0 до 9, и набор часто используют для проверки новых идей в этой области.
В предыдущей статье исследователи из Массачусетского технологического института представили метод «дистилляции» гигантских наборов данных в маленькие. В качестве подтверждения концепции они сжали MNIST до 10 изображений. Изображения не были выбраны из исходного набора данных. Их тщательно спроектировали и оптимизировали, чтобы они содержали объем информации, эквивалентный объему полного набора. В результате, при обучении на 10 этих изображениях ИИ-модель достигает почти такой же точности, как и обученная на всем наборе MNIST.

Примеры изображений из набора MNIST. WIKIMEDIA

10 изображенных, «дистиллированных» из MNIST, могут обучить ИИ-модель достигать 94-процентной точности распознавания рукописных цифр. Тунчжоу Ван и др.
Исследователи из университета Уотрелу хотели продолжить процесс дистилляции. Если возможно уменьшить 60 000 изображений до 10, почему бы не сжать их до пяти? Фокус, как они поняли, заключался в том, чтобы смешивать несколько цифр в одном изображении, а затем передавать их в модель ИИ с так называемыми гибридными, или «мягкими», метками. (Представьте лошадь и носорога, которым придали черты единорога).
«Подумайте о цифре 3, она похожа на цифру 8, но не на цифру 7, — говорит Илья Сухолуцкий, аспирант Уотерлу и главный автор статьи. — Мягкие метки пытаются запечатлеть эти общие черты. Поэтому вместо того, чтобы сказать машине: «Это изображение — цифра 3», мы говорим: «Это изображение — на 60% цифра 3, на 30% цифра 8 и на 10% цифра 0»».
Ограничения нового метода обучения
После того как исследователи успешно использовали «мягкие» метки для достижения адаптации MNIST под метод обучения «менее чем с одной» попытки, то начали задаваться вопросом, насколько далеко может зайти идея. Существует ли ограничение на количество категорий, которые ИИ-модель может научиться определять на крошечном количестве примеров?
Удивительно, но ограничений, похоже, нет. С помощью тщательно разработанных «мягких» меток даже два примера теоретически могут кодировать любое количество категорий. «Всего лишь двумя точками можно разделить тысячу классов, или 10 000 классов, или миллион классов», — говорит Сухолуцкий.
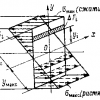
Разбивка яблок (зеленых и красных точек) и апельсинов (оранжевых точек) по весу и цвету. Адаптировано из презентации Джейсона Мейса «Машинное обучение 101»
Это то, что ученые показали в своей последней статье с помощью чисто математического исследования. Они реализовали эту концепцию с помощью одного из простейших алгоритмов машинного обучения, известного как метод k-ближайших соседей (kNN), который классифицирует объекты с использованием графического подхода.
Чтобы понять, как работает метод kNN, возьмем как пример задачу классификации фруктов. Чтобы обучить kNN-модель понимать разницу между яблоками и апельсинами, сначала нужно выбрать функции, которые вы хотите использовать для представления каждого фрукта. Если выбираете цвет и вес, то для каждого яблока и апельсина вы вводите одну точку данных с цветом фрукта в качестве значения x и весом в качестве значения y. Затем алгоритм kNN отображает все точки данных на двухмерной диаграмме и проводит границу посередине между яблоками и апельсинами. Теперь график аккуратно разделен на два класса, и алгоритм может решить, представляют ли новые точки данных яблоки или апельсины — в зависимости от того, на какой стороне линии находится точка.
Чтобы изучить обучение «менее чем с одной» попытки с помощью алгоритма kNN, исследователи создали серию крошечных наборов синтетических данных и тщательно продумал их «мягкие» метки. Затем они позволили алгоритму kNN построить границы, которые он видел, и обнаружили, что он успешно разбил график на большее количество классов, чем было точек данных. Исследователи также в значительной степени контролировали, где проходят границы. Используя различные изменения «мягких» меток, они заставляли алгоритм kNN рисовать точные узоры в форме цветов.
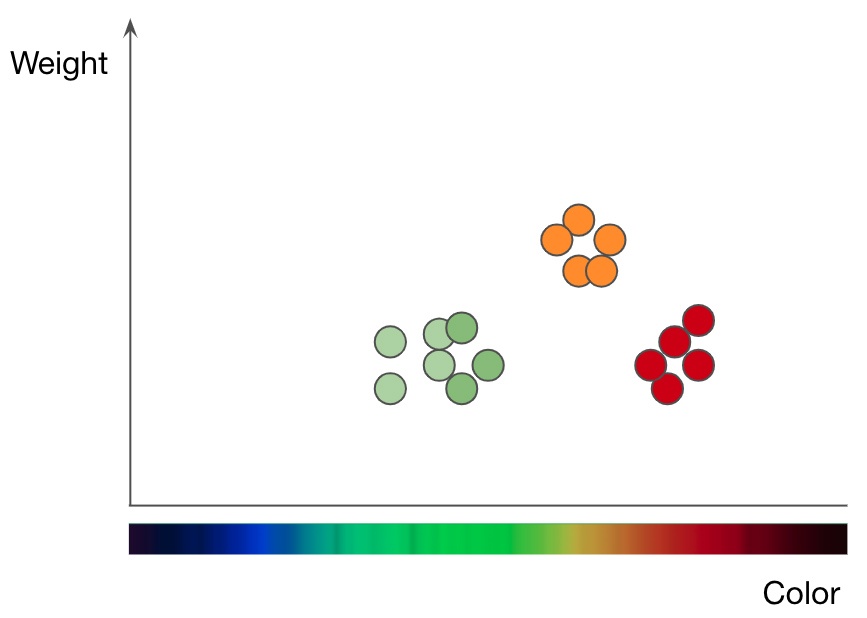
Исследователи использовали примеры с «мягкими» метками, чтобы обучить алгоритм kNN кодировать все более сложные границы и разбивать диаграмму на большее число классов, чем на ней есть точек данных. Каждая из цветных областей представляет собой отдельный класс, а круговые диаграммы сбоку от каждого графика показывают распределение мягких меток для каждой точки данных.
Илья Сухолуцкий и др.
Различные диаграммы показывают границы, построенные с помощью алгоритма kNN. На каждой диаграмме все больше и больше граничных линий, закодированных в крохотных наборах данных.
Конечно, у этих теоретических изысканий есть некоторые ограничения. В то время как идею обучение «менее чем с одной» попытки хотелось бы перенести на более сложные алгоритмы, задача разработки примеров с «мягкой» меткой значительно усложняется. Алгоритм kNN интерпретируемый и визуальный, что позволяет людям создавать метки. Нейронные сети сложны и непроницаемы, а это значит, что для них то же самое может быть неверным. Дистилляция данных, которая хороша для разработки примеров с «мягкой» меткой для нейронных сетей, также имеет значительный недостаток: метод требует, чтобы вы начали с гигантского набора данных, сокращая его до чего-то более эффективного.
Сухолуцкий говорит, что пытается найти другие способы создавать эти маленькие синтетические наборы данных — вручную или с помощью другого алгоритма. Несмотря на эти дополнительные сложности исследования, в статье представлены теоретические основы обучения. «Вне зависимости от того, какие наборы данных у вас есть, вы можете добиться значительного повышения эффективности», — сказал он.
Это больше всего интересует Тунчжоу Вана, аспиранта Массачусетского технологического института. Он руководил предшествующим исследованием дистилляции данных. «Статья опирается на действительно новую и важную цель: обучение мощных моделей на основе небольших наборов данных», — говорит он о вкладе Сухолуцкого.
Райан Хурана, исследователь из Монреальского института этики искусственного интеллекта, разделяет это мнение: «Что еще важнее, обучение «менее чем с одной» попытки радикально снизит требования к данным для построения функционирующей модели». Это может сделать ИИ более доступным для компаний и отраслей, которым до сих пор мешали требования к данным в этой области. Это также может улучшить конфиденциальность данных, поскольку для обучения полезных моделей нужно будет получать меньше информации от людей.
Сухолуцкий подчеркивает, что исследование находится на ранней стадии. Тем не менее, оно уже будоражит воображение. Каждый раз, когда автор начинает представлять свою статью коллегам-исследователям, их первая реакция — утверждать, что эта идея находится за гранью возможного. Когда они внезапно понимают, что ошибаются, то открывается целый новый мир.
Автор: derprimus