Сложение двух чисел с плавающей запятой без потери точности

Здравствуйте, друзья, как вы думаете, если мы напишем такой код:

s = a+b;
z = s-a;
t = b-z;

то не кажется ли вам, что в результате его выполнения получится, что t=0? С точки зрения привычной математики действительных чисел это и правда так, а вот с точки зрения арифметики с плавающей запятой в переменной t будет кое-что другое. Там будет то, что спасает нас от потери точности при сложении чисел и . Кого интересует данная тема, прошу под кат.

По моей традиции текстовая статья дублируется на видео. По содержанию текст и видео идентичны.

Читателю статьи для её восприятия нужно понимать способ представления чисел с плавающей запятой в формате IEEE-754 и понимать, почему, например, 0,1+0,2≠0,3, но если такого навыка у вас по каким-то причинам нет, но вы хотели бы его приобрести, то прошу обратить внимание на список источников конце статьи, на пункты [1] и [3-5].

Итак, у нас следующая проблема. Сумма двух чисел с плавающей запятой c=a+b может вычисляться с некоторой ошибкой. Знаменитый на весь интернет пример 0,3 ≠ 0,2+0,1 хорошо это показывает. Наша задача в том, чтобы всё-таки складывать числа без этой ошибки. То есть сделать так, чтобы мы могли как-то сложить 0,2+0,1 и хоть в каком-то виде знать точный результат. В каком смысле точный, если даже исходные числа 0,1 и 0,2 не имеют точного представления в формате IEEE-754? Вот сейчас и поясню.

Начнём с того, что чисел 0,1 и 0,2 в двоичной арифметике с плавающей запятой быть не может, а наиболее близкие к ним значения для типа данных double (число удвоенной точности binary64, так его называют в Стандарте IEEE-754) следующие:

Десятичный результат получен с помощью правильного онлайн-конвертера, а дробь посчитана с помощью библиотеки MPIR и функции mpq_set_d, которая умеет переводить double к рациональной дроби.

К сожалению, это данность, от неё никуда не уйти, если хранить числа в типе данных double (или любом другом типе фиксированного размера из Стандарта IEEE-754). Но проблема, которую мы решаем, другая. Нам нужно эти два числа, наиболее близких к 0,1 и 0,2, сложить так, чтобы получить результат без погрешности. То есть чтобы в результате сложения иметь число

0,1000000000000000055511151231257827021181583404541015625 +
0,2000000000000000111022302462515654042363166809082031250 =
0,3000000000000000166533453693773481063544750213623046875.

К сожалению, если просто написать код s=0.1+0.2, то мы получим кое-что другое, а именно

s == 0.3000000000000000444089209850062616169452667236328125

что отличается от правильного ответа ровно на

«Подумаешь, — скажете вы, — десять в минус семнадцатой! Мне чтобы пиксель на экран вывести такая погрешность не помеха!». И будете правы. Задача точного вычисления каких-либо выражений относится к очень узкой области Computer Science, связанной с разработкой математических библиотек для языков программирования. Когда вы вызываете какую-нибудь функцию из такой библиотеки, то можете и не подозревать, что в основе её работы лежит труд десятков и сотен человек, выполняемый на протяжении десятилетий, а работает такая функция правильно благодаря совершенно неочевидным алгоритмам… Вот я и хотел бы приоткрыть для вас этот удивительный мир, для чего и пишу такие научно-популярные статьи.

Зачем может понадобиться точное сложение двух чисел? Приложений много, но вот одно из них, которое будет понятно всем. Если вы хотите сложить все числа из массива X[N] и сделаете это вот так:

S = 0.0;
for (i=0; i<N; ++i)
  S = S + X[i];

то вы получите, мягко говоря, довольно большую погрешность. Если же применить знания, описываемые в этой статье, то можно написать алгоритм, который имеет погрешность значительно меньше. Но подробности такого алгоритма я рассмотрю в другой статье, ради которой и пишу эту.

Итак, теперь давайте я опишу проблему чуть более формально. В рамках статьи представьте, что всё происходит в типе данных double, это никак не изменит сути изложения.

У нас есть два числа и типа double. Нам не важно, что эти числа и уже содержат в себе какую-то погрешность, полученную, например, в результате конвертирования десятичной строки в формат IEEE-754. Важно, что они сейчас перед нами, а их предыстория нас не интересует. Нужно сложить эти два числа c=a+b так, чтобы в результате сложения не возникло погрешности.

Но ведь это невозможно!

Да, это невозможно, спасибо что дочитали, до новых встреч :)

Шучу, конечно. Это невозможно только если мы храним результат сложения в одной переменной того же типа данных. Но вспомните пример выше. У нас была переменная s, и переменная t. Причём s была округлённым результатом сложения a+b, а t была равна разности этого округлённого результата и точного значения суммы. При этом выполняется равенство s+t=a+b.

И вот хорошая новость состоит в том, друзья, что такое представление суммы a+b в виде суммы s+t можно выполнить всегда (если a+b≠∞)! Если s=a+b оказывается точно-представимым значением в типе double, то очевидно, что t=0. Если это не так, то t будет равно некоторому очень маленькому (по сравнению с s) числу, которое является точно-представимым. Итак, вот оно, фундаментальное свойство суммы чисел с плавающей запятой: ошибка округления в результате суммирования чисел типа double всегда будет точно-представимым числом типа double! А это означает, что пара чисел (s, t) всегда даёт нам возможность сохранить сумму чисел a+b «как бы» без погрешности. Да, мы вынуждены хранить две переменные вместо одной, но прелесть в том, что их всего две, а не больше.

Теперь опишем это свойство на математическом языке. Введём обозначение RN(x) – это результат приведения произвольного вещественного числа x к типу данных double по правилу округления round-nearest-ties-to-even, то есть это округление к ближайшему, но в случае равного удаления от двух ближайших к тому, у которого последний бит мантиссы равен нулю (чётный). Именно этот режим работает почти везде по умолчанию, то есть если вы не знаете, о чём я сейчас говорю, то в вашем процессоре на 100% работает именно этот режим, так что не беспокойтесь.

Пусть a и b – числа типа double. Пусть |a|≥|b| и RN(a+b) ≠ ∞. Тогда следующий алгоритм

s = RN (a+b);
z = RN (s-a);
t = RN (b-z);
return (s, t);

вычисляет пару (s, t) таких чисел, для которых:

1. s+t = a+b (в точности)
2. s – число типа double, наиболее близкое к a+b.

Основная цель моих статей — объяснять сложные вещи простым языком, поэтому давайте я построю для вас образ, помогающий понять этот алгоритм. Пожалуйста, посмотрите на рисунок, а ниже даётся его описание.

Прямоугольник олицетворяет переменную с плавающей запятой фиксированного размера, поэтому прямоугольники, помеченные символами «а» и «b» имеют одинаковый размер, но смещён относительно вправо, потому что у нас есть условие: |a|≥|b|. Третий прямоугольник «Точное а+b» — это некоторое промежуточное значение, которое может иметь больший размер, чем размер переменных и , поэтому оно будет округлено, и «хвостик», вылезающий за границы нашего типа данных, будет отброшен. Таким образом, мы переходим к четвёртому прямоугольнику «Округлённое a+b», это и есть наше значение s, полученное в первой строке алгоритма. Если теперь из s снова вычесть , то останется только «b без хвостика». Это делается во второй строке алгоритма. Теперь мы хотим получить «хвостик» от , и это делается в третьей строке алгоритма, когда из исходной переменной мы вычитаем «b без хвостика». Остаётся «хвостик», это и есть переменная t, которая показывает ту самую погрешность, которая возникла в ходе округления. При этом из данных рассуждений видно, что такой «хвостик» всегда будет умещаться в одну переменную, потому что он не может превышать размера переменной . В крайнем случае, когда смещение относительно будет настолько большим, что s=RN(a+b)=a, то в этом случае, очевидно, z=0 и t=b. Скучный рисунок на эту тему я вам предлагаю изобразить самостоятельно.

Если вы не находите картинки убедительными для себя, то в книге [1, раздел 4.3.1, теорема 4.3] есть строгое математическое доказательство, но оно не умещается в формат научно-популярной статьи. Его краткая суть в том, что в нём показано почему в строках 2 и 3 алгоритма не будет выполняться округления, то есть эти выражения вычисляются точно, а если так, значит t=b-z=b-(s-a) = (a+b)-s в точности, что нам как раз и нужно: t является разностью между реальной суммой a+b и её округлённым значением s.

Давайте рассмотрим несколько примеров, удобных для восприятия человека.

Пример 1.

Пояснение. Реальное значение a+b=2⁵³+1, однако в типе данных double младший бит, равный единице, не влезет в 52 бита дробной части мантиссы, по какой причине будет выброшен при округлении, но переменная t «подхватит» его и сохранит в качестве погрешности, а переменная s сумеет сохранить только 2⁵³ ровно. Легко видеть, что s+t будет равно 2⁵³+1.

Пример 2.

Пояснение выполнено в двоичном коде.

  a = 1000000000000000000000000000000000000000000000000000000000000
  b =                                111111111111111111111111111111
a+b = 1000000000000000000000000000000111111111111111111111111111111
      -------------------------------------бит округления--^ 
  s = 1000000000000000000000000000001000000000000000000000000000000

Если выравнивание кода не поехало, то вы видите, где у суммы a+b будет бит округления, и что само округление будет выполнено вверх. Чтобы снова получить паровоз из 30 единиц, нужно вычесть единицу из s=2⁶⁰+2³⁰. Поэтому t=-1. Как видим, t может быть отрицательным, когда округление выполняется вверх.

Я не говорил этого явно, но алгоритм работает даже когда b<0, то есть фактически происходит вычитание.

Пример 3.

В этом примере число является сдвигом вправо на 2 бита числа , поэтому если влезает в double «впритык», ясно, что вычитание здесь точным получиться не может. Останется небольшой хвостик размером в два бита после запятой.

Из доказательства, приведённого в [1], следует один положительный момент данного алгоритма: в ходе его выполнения не может возникнуть переполнения во второй и третьей строках, если оно не возникло при вычислении s=RN(a+b).

Недостатком является то обстоятельство, что алгоритм работает только для |a|≥|b| (однако если вы посмотрели доказательство, то знаете, что в действительности достаточно более слабого условия, чтобы экспонента была не меньше экспоненты , но проверить это условие намного сложнее). То есть нам нужно либо делать лишнюю проверку, либо как-то иначе гарантировать правильный порядок чисел на входе алгоритма. Ветвление не всегда обрабатывается достаточно быстро, это зависит от процессора и от того, как на это ветвление посмотрел компилятор (иногда он может его убрать, иногда — нет, а иногда он его убрал, но оказалось так плохо, что лучше бы не трогал). Возникает вопрос: а можно сложить числа без ошибок округления, если их порядок друг относительно друга заранее неизвестен?

Можно. Для этого есть второй алгоритм, но в нём вместо 3-х операций их уже 6.

  s = RN (a+b);
  b' = RN (s-a);
  a' = RN (s-b');
  d_b = RN (b-b');
  d_a = RN (a-a');
  t = RN (d_a+d_b);
  return (s, t)

Как это работает? В случае когда |a|≥|b|, алгоритм работает по сути так же как предыдущий, и строгое доказательство для этого случая, которое вы можете отыскать в [2, раздел 2.3, теорема 7], сводится к тому, чтобы показать, что «лишние» три операции не портят этого результата. А вот основная сложность доказательства в том, чтобы рассмотреть случай |a|<|b|, он значительно труднее и тоже выходит за рамки лёгкого научно-популярного изложения. Схематичная картинка общей ситуации при |a|<|b| даётся ниже с пояснением.

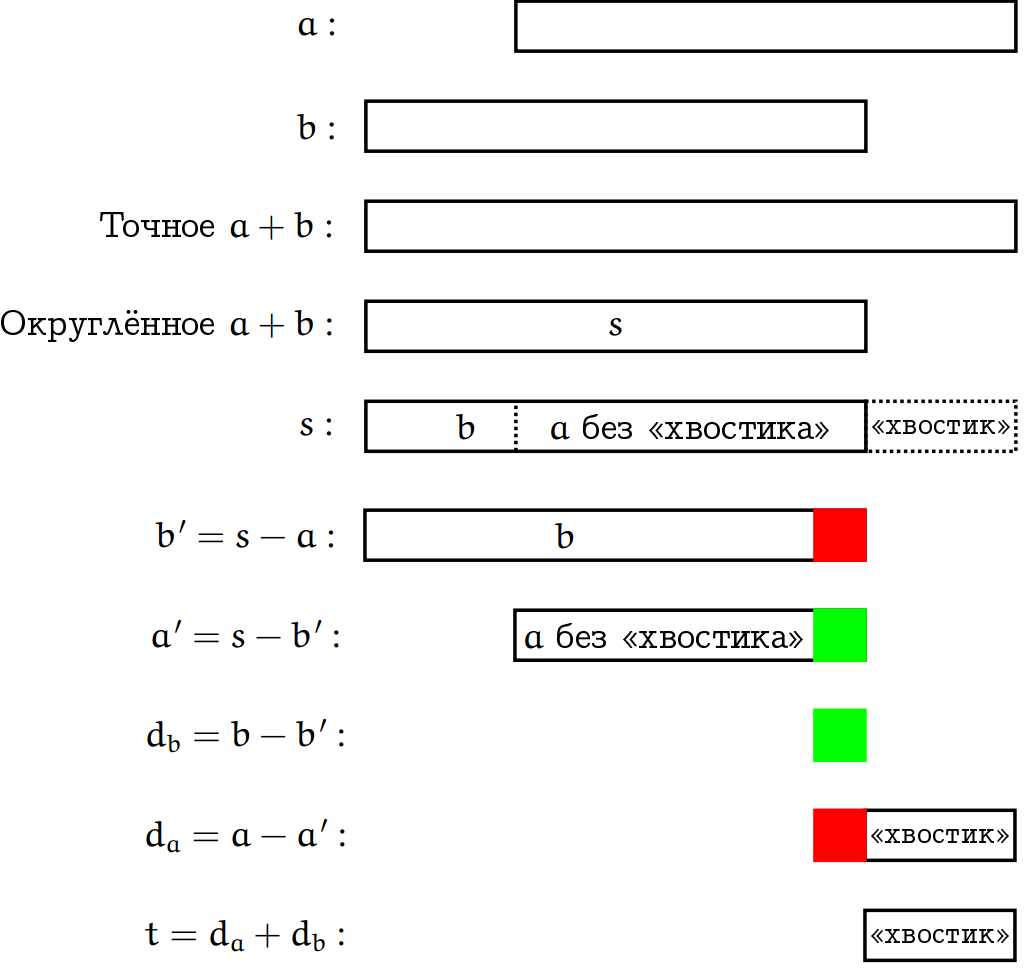
Первые два прямоугольника показывают соотношение между и , на этот раз смещено относительно вправо. Следующие три прямоугольника показывают процедуру сложения и отбрасывания «хвостика». Дальше начинается основная сложность. Вычисляем b’=s-a, то есть мы вычитаем из округлённого значения s число и выброшенный «xвостик», а это значит, что b’ будет чуть меньше, чем , и этот недостаток отмечен красным прямоугольничком. Другое дело, когда мы вычисляем a’=s-b’, то есть вычитаем из суммы величину «b с недостатком», а значит получим «а без хвостика с избытком», и этот избыток обозначается зелёным прямоугольничком. Если мы теперь вычтем из величину b’ (которая с недостатком), то получим избыток d_b. Далее вычитаем из величину a’ (которая с избытком), и получаем хвостик с недостатком d_a. Если теперь сложить хвостик с недостатком и избыток, мы получим «чистый хвостик».

У читателя может возникнуть вопрос: а в каких случаях можно с уверенностью сказать, что t=0? Иными словами, про какие пары чисел (a, b) точно известно, что их сумма будет точно-представимым (без округления) числом в том же типе данных?

Мне известны только три теоремы на этот счёт, которые также приводятся в [1] и [2].

Теорема 1 [книга 1, раздел 4.2.1, теорема 4.2]. Если сумма RN(a+b) оказалась денормализованным числом, то сумма a+b является точно-представимой.

Теорема 2 [статья 2, раздел 2.2, лемма 4] Если |a+b|≤|a| и |a+b|≤|b|, то число a+b является точно-представимым (аналогичное верно и для разности).

Теорема 3 [книга 1, раздел 4.2.1, лемма 4.1] Пусть a≥0 и a/2 ≤ b ≤ 2a, тогда разность a-b будет точно представимой.

Бдительный читатель сразу вспомнит про так называемую ошибку критического сокращения старших значащих битов, называемую в литературе “Catastrophic Cancellation” и спросит: «Как же так, ведь давно известно, что когда мы вычитаем очень близкие друг к другу числа, там возникает такая погрешность, что ой-ой-ой! Как ты говоришь, что в этом случае разность будет точно-представимой».

Дело в том, что Catastrophic Cancellation – это не ошибка вычисления, а неизбежное свойство чисел с плавающей запятой; это свойство не порождает никакую новую погрешность, а как бы «высвечивает» ту, что уже изначально была заложена в уменьшаемом и вычитаемом. Если не смотря на уже имеющееся в интернете описание вы хотите подробного обсуждения данной особенности чисел с плавающей запятой именно в моём исполнении, то пишите об этом в комментариях, пойду навстречу.

На основе рассмотренных в этой статье алгоритмов в следующей мы будем более правильно складывать числа из массива.

Благодарю за внимание!

Список источников

[1] Jean-Michel Muller, “Handbook of floating-point arithmetic”, 2018.
[2] Jonathan Richard Shewchuk, “Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates”, Discrete & Computational Geometry 18(3), 1997, pp. 305–363.
[3] На Хабре: «Что нужно знать про арифметику с плавающей запятой».
[4] На Хабре: «Наглядное объяснение чисел с плавающей запятой».
[5] Учебный видео-курс для «самых маленьких», предельно наглядное разъяснение чисел с плавающей запятой в 8-ми уроках. Первый урок на на YouTube.

Автор: Артём Караваев

Источник