Современному программисту, математику или аналитику часто приходится проектировать, а то и создавать программно-аппаратные комплексы для работы с большими массивами числовых данных. Построение имитационных моделей, прогнозирование, расчёт статистики, управление оперативными процессами, финансовый анализ, обработка экспериментальных данных — везде требуется получить максимальную скорость вычислений на единицу затрат.
При этом большинство ну хотя бы минимально сложных и функциональных систем (во всяком случае, из тех, что встречались лично мне за 8 лет работы в банковской сфере), как правило, гетерогенны — состоят из множества функциональных блоков, как пёстро сшитое лоскутное одеяло, где каждый лоскуток выполняется разным приложением, зачастую даже на различных аппаратных платформах. Почему? Да просто это рационально и удобно. Каждый продукт хорош в своей области. Например, экономисты любят использовать Ms Excel для анализа и визуализации данных. Но мало кому в голову придёт использовать эту программу для обучения серьёзных искусственных нейросетей или решения дифференциальных уравнений в реальном времени — для этого зачастую приобретаются (или уже приобретены компанией) мощные универсальные пакеты, предлагающие гибкий API, или под заказ пишутся отдельные модули. Вот и получается, что результат считать выгоднее в том же Matlab, хранить в таблицах СУБД Oracle (запущенной на кластере Linux), а отчёт показывать пользователям в приложении Excel, работающем как OLE server на Windows. Причём связаны все эти компоненты одним из универсальных языков программирования.
Как выбрать оптимальную среду реализации для конкретной задачи? Вы сталкиваетесь с компромиссом: одни инструменты или библиотеки Вам лучше знакомы, другие обладают большей функциональностью (скажем, поддерживают ООП), третьи имеют преимущество в скорости выполнения (например, используют SSE-векторизацию, как C++), четвёртые обеспечивают высокую скорость разработки (например, Visual Basic). На рынке в наши дни предлагается внушительное количество как программных средств — компиляторов, систем компьютерной математики, офисных пакетов, так и аппаратных технологий (x86-x64, Cell, GPGPU) и средств организации их совместной работы (сети, кластеры, облачные вычисления).
Добавьте к этому тренды в использовании вычислительных ресурсов (массовый переход к параллельным вычислениям, виртуализации приложений и серверов), новые модели предоставления вычислительных мощностей (такие как Amazon EC2), новые методы обеспечения отказоустойчивости, нюансы лицензирования — и Вы получите гигантское количество комбинаций. Как выбрать оптимальную?
Основная рекомендация — сначала делайте прототип в среде с наиболее высокой скоростью разработки, затем переходите к более трудоёмким вариантом, пытаясь улучшить метрики производительности (например, уменьшить время выполнения), пока не исчерпаете лимит времени на решение данной подзадачи. В то же время, не стоит тратить силы на заведомо немасштабируемое решение. Не ленитесь, обязательно пишите код и тестируйте его «вживую», проверяя свои догадки. Теоретические знания и чуткая интуиция — это прекрасно, но очень часто реальность отличается от наших моделей и представлений, как Вы увидите по моему опыту решения небольшой производственной задачи.
На днях мне понадобилось оптимизировать выполнение простенького алгоритма: подсчёта суммы синусов всех целых чисел от 1 до двухсот миллионов. На самом деле, конечно, реальный алгоритм был несколько иным, но я искал оптимальный инструмент для решения схожего класса задач, строить полную инфраструктуру в каждом прототипе на начальном этапе не имело смысла, поэтому я упростил алгоритм до предела. Если Вы задаётесь вопросом, для чего могут понадобиться алгоритмы подобного вида, напомню, что тригонометрические функции могут использоваться, например, как пороговые функции активации для искусственных нейронных сетей. Спойлер: результаты исследования оказались для меня полной неожиданностью!
Постановка задачи:
Рабочий стенд: Dual Xeon E5 2670 @2.6 Ghz с включённой технологией энергосбережения, снижающей частоту CPU во время простоя, 2x8 физических ядер с гипертредингом, 128 Gb памяти DDR3-1600 на платформе Windows Server 2008R2.
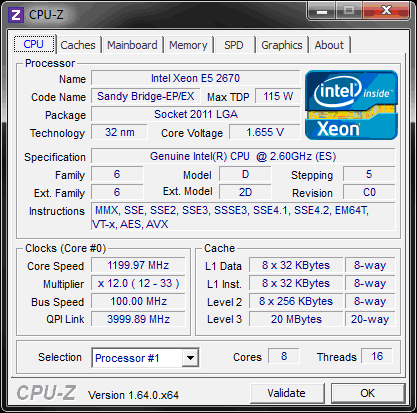
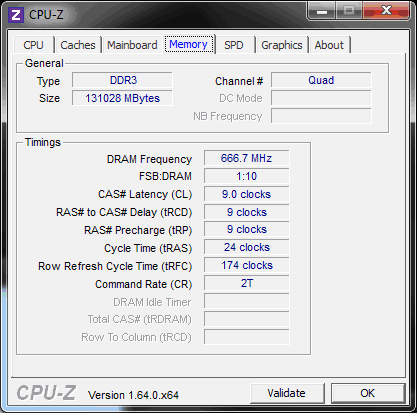
Двойная точность (double, т.е. один из стандартных форматов сопроцессора x86) для начала нас вполне удовлетворит. Давайте посмотрим, как с задачей расчёта суммы синусов справятся разные компиляторы, а затем и разные вычислительные архитектуры. В забеге участвуют: Maple 12, Maple 17, MatLab R2013a, Visual Basic 6.0, Visual Basic.NET и Visual C++ 2012 (в общем, те, кто оказался по рукой). Все замеры времени сделаны после повторного запуска, и соответствуют среднему затраченному времени.
Знаю, методика тестирования не самая строгая — всего один тип процессора, одна ОС, упрощённая методика замера производительности. Однако у нас ведь не научная статья, поэтому ограничимся наиболее интересными фактами. Я не буду вдаваться в подробности организации межкомпонентных коммуникаций (как правило, для Win достаточно компонентов COM и обычных dll, ну и совместного доступа к памяти), просто посмотрим, какая комбинация позволит наиболее быстро вычислить нужный результат. Для начала узнаем, какой инструмент сгенерирует наиболее быструю однопоточную версию, а затем распараллелим её, хорошо?
Начнём с Maple:
st := time():evalhf(sum(sin(i),i=1..200000000));time() - st;
Результат Maple 12:
1.25023042417602160 за 54.304 сек.
Результат Maple 17:
1.25023042417610020 за 19.656 сек.
На первый взгляд, отличная работа инженеров MapleSoft. На 75% улучшили время выполнения от версии к версии продукта. Давайте посмотрим, сможет ли 17-я версия ещё и откомпилировать эту процедуру. Наивно вызвав
cp:=Compiler:-Compile(proc(j::integer)::float;local i::integer: evalhf(sum(sin(i),i=1..j)) end proc:):
получим процедуру, которая почему-то при любом раскладе выдаёт ноль. Пробуем альтернативу — явный цикл.
p2 := proc(j::integer)::float;local i::integer,res::float;res:=0; for i from 1 to j do: res:=res+evalhf(sin(i)):end do; res end proc:
Если запускать p2 без компиляции, результата можно и не дождаться! По крайней мере, я подождал минут 10 и сдался. Видимо, для среды выполнения Maple функция sum существенно оптимизированна по сравнению с циклом. Однако же
cp2:=Compiler:-Compile(p2): st := time():cp2(200000000);time() - st;
в Maple 17 даёт превосходный результат:
1.25023042417610020 за 9.360 сек!
Несмотря на «закидоны» системы, проявив упорство и изобретательность, мы смогли получить отличный прирост производительности :-)
Переходим к Microsoft Visual Studio 2012
Я хорошо помню, как в своё время меня глубоко разочаровала платформа Net ужасной медлительностью своего откомпилированного кода. Мой тестовый пример (откомпилированный!) в VB.Net 2003 выполнялся раз в 8 медленнее кода на VB6, поэтому я не питал особых иллюзий, собирая проект под VB.Net 2012.
Public Class Form1
Private Sub Form1_Load(sender As Object, e As EventArgs) Handles MyBase.Load
Dim i As Long, res As Double, tm As DateTime
tm = Now
For i = 1 To 200000000
res = res + Math.Sin(i)
Next
TextBox1.Text = res & vbNewLine & Now.Subtract(tm).TotalSeconds.ToString("0.000")
End Sub
End Class
Как оказалось, зря!
Результат VB.Net 2012:
1.25023042417527 за 11.980 сек., неплохо!
Основные надежды я, конечно же, возлагал на оптимизирующий компилятор Visual C++, собираясь откомпилировать в родной исполняемый код, без всякого Net-овского шлака, следующую процедуру:
#include <iostream>
#include <windows.h>
using namespace std;
int main()
{
double res=0.0;
int dw = GetTickCount();
for (int i = 1; i <= 200000000; i++)
res+=sin(i);
cout.precision(20);
cout << "Result: " << res << " after " << (GetTickCount()-dw);
}
Ключи использовал /O2 и /Ot:
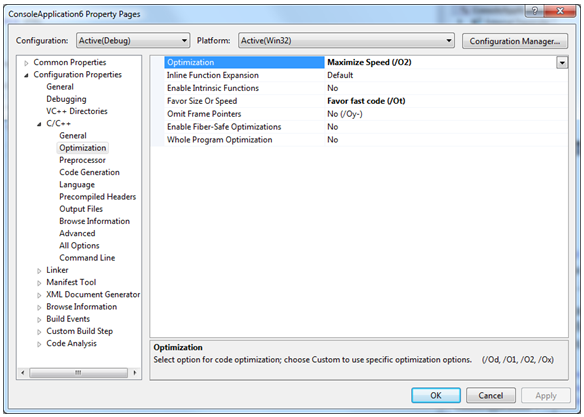
Результат VС++.Net 2012:
вообще не впечатлил: 1.2502304241761002 за 11.404 сек.
Подошла очередь олдскульного VB6
Код выглядит очень просто:
res = 0: for i = 1 To 200000000: res = res + Sin(i) : Next i
Компилируем с максимальной оптимизацией:
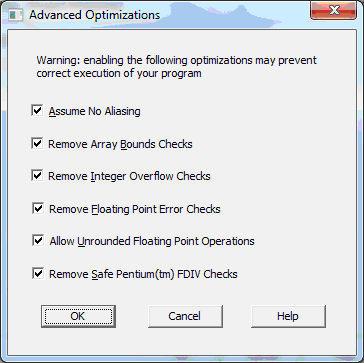
И получаем чемпиона в лице VB6:
Result: 1.25023042417543, Time spent: 0:00:09 (9.092153)
Вот теперь объясните мне, как продукт 12-летней давности уделывает новые компиляторы по всем параметрам?! Такое ощущение, что MS деградирует, но это уже тема другого разговора. Если заглянуть в листинг дизассемблера, видно, что компилятор VC++ честно векторизовал код:
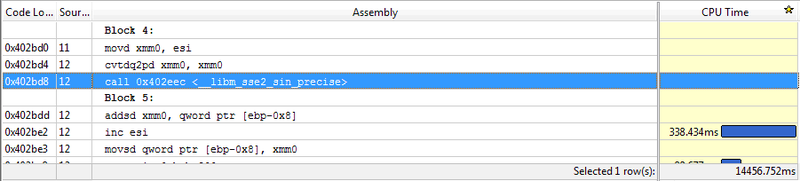
Правда, я не знаю деталей этой реализации синусов на SSE2, однако какой в ней прок, если она проигрывает стековым однооперандным командам FPU, которые использовал Visual Basic 6? Скажу по секрету, после такого неприятного открытия я скачал пробную версию Intel Parallel Studio XE 2013 и пересобрал проект в компиляторе Intel C++ 13 с ключами QxSSE4.2, а затем и QxAVX — результаты стали ещё хуже, в районе 13-15 секунд. После таких результатов возникла дикая мысль — а может, не всё в порядке с процессорами моего сервера? Запустил сравнение VB6 и VC++2012 на другой машине, стареньком Core Duo 6600 с двумя ядрами. Отставание SSE-версии ещё больше. Единственное логическое объяснение — начиная с архитектуры Core, инженеры Intel значительно повысили производительность операций FPU по сравнению с SSE, а разработчики компиляторов Microsoft и Intel этот факт упустили из вида.
На картинке выше Вы, кстати, могли наблюдать, что профилировщик Vtune Amplifier в режиме Hot Spots не справился с вычислением таймингов для SSE-инструкций. Если верить ему, то самая трудоёмкая операция в моём коде — это увеличение счётчика цикла! Из академического интереса, раз уж пакет от Intel был установлен, я прогнал модуль через продукт Advisor XE 2013, призванный показать места в коде, которые можно распараллелить. В коротком цикле без зависимостей по данным, без совместно используемых ресурсов, ИДЕАЛЬНО подходящем для параллельного выполнения, сей продукт таких мест обнаружить не смог. Ну и как доверять этой программе в более сложных случаях? Всё чаще возникает ощущение, что программисты Intel выпускают продукты хотя и хорошо разрекламированные, но малопригодные для практики (да и не только программисты, если вспомнить кукурузные анонсы и переанонсы Larrabee и Knights Corner). Ну ладно, у нас же ещё остался Matlab.
Эксперимент с Matlab приятно удивил
Набрав
tic;sum(sin(1:200000000));toc;
почти сразу видим результат:
1.250230424175050, Elapsed time is 3.621641 seconds.
Ну и ну! Оказалось, что умный Матлаб сразу распараллелил это выражение по числу физических ядер на моей локальной машине, обеспечив их полную загрузку. Приятно, не правда ли? Я ведь заплатил за мощное железо и хотел бы, чтобы софт (тоже, кстати, отнюдь не дешёвый) использовал его на все 100%. Респект инженерам MathWorks!
Попробуем откомпилировать? Для этого переносим выражение в m-файл. И тут нас поджидает очередной сюрприз. Неоткомпилированное tic;FastSum(200000000);toc; даёт Elapsed time уже 5.607512 секунд. Кто уже с таким сталкивался, в чём тут дело? Для меня пока загадка. Пользуемся помощью команды deploytool, ждём энное количество минут, и Матлаб создаёт для нас здоровенный экзешник в полмегабайта. Даа, команде разработчиков компилятора есть ещё над чем поработать — для сравнения, размер VC++ — 46Kb, VB.Net — 30Kb, Vb6 — 36Kb. Но что же нам выдаст откомпилированный Matlab исполняемый файл?
1.2502, Elapsed time is 10.716620 seconds.
В откомпилированной версии, как видно, автоматическое распараллеливание цикла почему-то пропадает. Сердце мне подсказывает, что компания хочет дополнительную денежку за Parallel Computing Toolbox :-)
В любом случае, по однопотоку у нас лидер VB6, поэтому я написал в этой среде простенький Active Exe сервер, позволяющий распараллелить наши вычисления по заданному числу потоков:
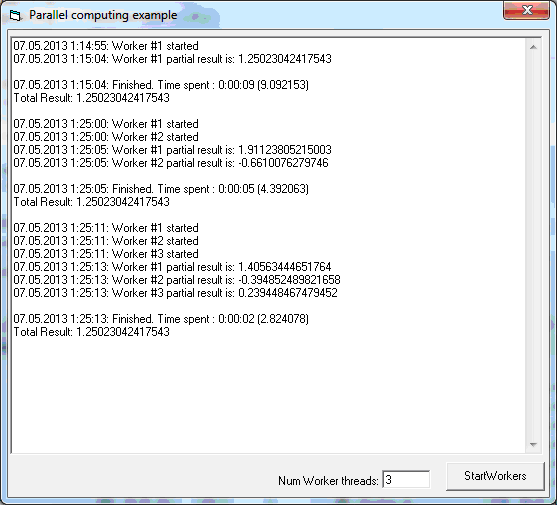
Давайте посмотрим, насколько хорошо масштабируется наше решение при увеличении числа рабочих потоков от 1 до 32. Если честно, я был уверен, что производительность будет расти, пока не упрётся в потолок в виде количества физических ядер процессоров, ибо откуда виртуальным ядрам HT взять ресурсы для работы с плавающей точкой, если конвейер FPU уже полностью занят?
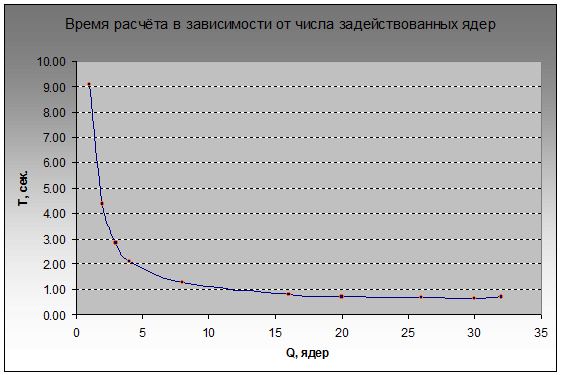
Тем не менее, дополнительно задействовав 14 логических ядер, удалось сократить время выполнения на 20%: с t(16) = 0.803 сек. до t(30)=0.645. Возможно, результат был бы более внушительным, если бы процессоры изначально не находились в режиме экономии энергии, ибо за 0,6 секунд, похоже, они просто не успевают нарастить тактовую частоту до максимума.
GPGPU
Что ж, оптимальное решение для мейнстримной конфигурации в нашем конкретном случае мы нашли. Но не будем забывать про GPGPU (графические карты с возможностью проведения универсальных вычислений), которыми в наши дни оснащается всё больше серверов, и уж почти наверняка оснащены все домашние компьютеры и новые ноутбуки. Не стал исключением и мой стендовый сервер — специально под многопоточные вычисления был приобретён экс-флагман Nvidia, двухчиповая видеокарта GTX 590 с архитектурой Fermi, поддерживающая технологию CUDA.
Вообще должен сказать, что безмерно уважаю Nvidia. Во-первых, за то, что это, пожалуй, единственная компания, действительно продвигающая высокопараллельные вычисления в массы (конференции, семинары, акции, активная разработка и совершенствование ПО и архитектуры), во-вторых, за то что она сумела наладить продажи специализированного «железа» и выйти в лидеры в новом для себя секторе high-performance computing. Да, решения от AMD (ATI) мощнее, у карт AMD, возможно, больше гигафлопсов, но вы попробуйте начать разработку под FireStream — на сайте AMD не найдёте ни толковой документации, ни внятного описания самой технологии. Такое ощущение, что программисты/маркетологи/руководство AMD просто похоронили работу талантливых инженеров ATI. Так что наш выбор пока CUDA! Кстати, если у Вас возникли проблемы при интеграции CUDA 5 и Visual Studio 2012, можно воспользоваться рекомендациями этой статьи.
Итак, какими же ресурсами располагает наш чудо-дивайс?
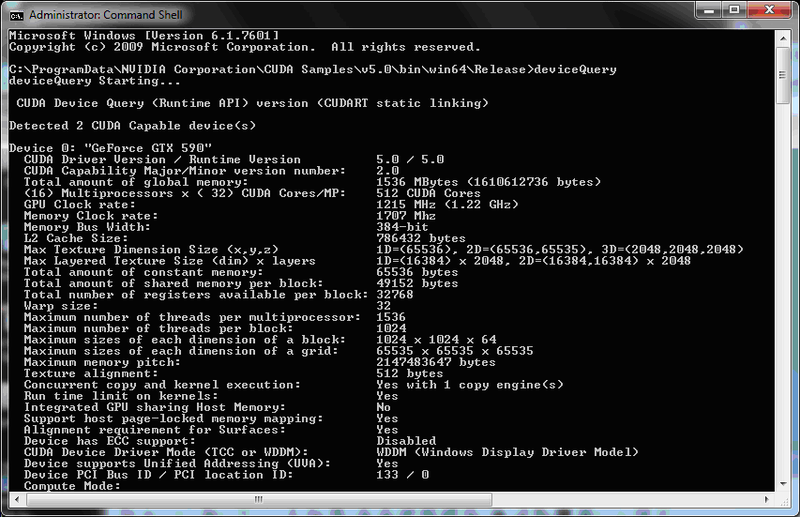
Как видно, теоретически мы можем запустить вычисления в 16*1536*2=49152 потока на двух устройствах GPU. На самом деле всё не так радужно — синусы в Fermi считаются в Special Functions Units, коих приходится 4 на мультипроцессор (SM). Итого мы можем рассчитывать одновременно не более 16*4*2=128 значений (опять же теоретически).
Не хотелось бы вот так сразу вдаваться в подробности архитектуры CUDA, тем более в тонкости оптимизации под CUDA — это и наука, и искусство сами по себе. Поэтому давайте начнём с быстрого прототипа в библиотеке Thrust, призванной повысить продуктивность труда программистов за счёт высокого уровня абстракции модели CUDA, в пику более низкоуровневому CUDA C.
Прелесть Thrust в том, что, по уверениям создателей, разработчикам теперь не нужно тратить время на самостоятельную реализацию таких примитивов, как арифметические операции, сортировка, всевозможные редукции (термин, который наверняка прочно вошёл в лексикон большинства программистов именно после знакомства с руководствами по CUDA), поиск, реорганизацию массивов и другие виды операций. Кроме того, эта библиотека самостоятельно определяет оптимальную конфигурацию запуска, и Вам не нужно зацикливаться на определении оптимального соотношения числа блоков и потоков GPU, как раньше...
Хотя Thrust и не задействует автоматически все CUDA-совместимые устройства, а выбирает одно самое быстрое, в любом случае, я ожидал безоговорочной победы числодробилки от Nvidia, хотя и знал о пониженной производительности при вычислениях двойной точности. Ведь одно дело рассчитать двести миллионов синусов, нужно ещё провести эффективную редукцию всего этого массива к одному суммарному значению, с чем высокопараллельные алгоритмы справляются обычно очень хорошо.
Мы будем использовать мощную функцию transform_reduce, позволяющую преобразовывать и суммировать элементы массива за один логический шаг. Создадим для неё специальный функтор sin_op. Код достаточно прост:
#include <thrust/transform_reduce.h>
#include <thrust/device_vector.h>
#include <thrust/host_vector.h>
#include <thrust/functional.h>
#include <thrust/sequence.h>
#include <windows.h>
using namespace std;
template <typename T>
struct sin_op
{
__host__ __device__
T operator()(const T& x) const {
return sin(x);
}
};
int main(void)
{
int dw = GetTickCount();
int n=10;
double res=0.0;
sin_op<double> tr_op;
thrust::plus<double> red_op;
thrust::device_vector<int> i(200000000/n);
for (int j=1;j<=n;j++)
{
thrust::sequence(i.begin(), i.end(),200000000/n*(j-1)+1);
res = thrust::transform_reduce(i.begin(), i.end(), tr_op, res, red_op);
}
cout.precision(20);
cout << res << endl<< "Total Time: " << (GetTickCount()-dw) << endl;
}
Я использую внешний цикл, чтобы гарантированно получать нужные объёмы памяти на устройстве — как ни печально, Thrust с этим самостоятельно справляется не всегда. По логике, нить должна бы вычислять свой целочисленный индекс, применять к нему трансформирующий функтор, и сохранять результат в быструю разделяемую память. Итак, компилируем, запускаем:
1.2502304241755013 за 1.704 сек.
Разочарованию нет предела. Результат какбэ намекает, что библиотека заставляет ускоритель делать не совсем то, что мы нарисовали в своём воображении. И действительно, если посмотреть на подробные тайминги, окажется, что библиотека пытается для начала разместить огромный массив нулей в относительно медленной основной памяти устройства (на что тратит 35% времени), затем перезаписывает эти нули натуральным рядом 1,2,3… (40% времени), ну и уж оставшиеся 25% времени занимается вычислением синусов и непосредственно суммированием (редукцией по оператору plus, причём тоже в медленной основной памяти).
Погрустив, вспоминаем, что в этой библиотеке есть виртуальные итераторы (fancy iterators). Смотрим в документации — ну точно,
While constant_iterator and counting_iterator act as arrays, they don’t actually require any memory storage. Whenever we dereference one of these iterators it generates the appropriate value on-the-fly and returns it to the calling function.
Подсчитывающий итератор — то, что доктор прописал:
#include <thrust/iterator/counting_iterator.h>
#include <thrust/transform_reduce.h>
#include <thrust/device_vector.h>
#include <thrust/host_vector.h>
#include <thrust/functional.h>
#include <thrust/sequence.h>
#include <windows.h>
using namespace std;
template <typename T>
struct sin_op
{
__host__ __device__
T operator()(const T& x) const {
return sin(x);
}
};
int main(void)
{
int dw = GetTickCount();
double res=0.0;
sin_op<double> tr_op;
thrust::plus<double> red_op;
thrust::counting_iterator<int> first(1);
thrust::counting_iterator<int> last = first + 200000000;
res = thrust::transform_reduce(first, last, tr_op, res, red_op);
cout.precision(20);
cout << res << endl<< "Total Time: " << (GetTickCount()-dw)<< endl;
}
Что по времени выполнения? Уменьшили почти вдвое, избавившись от неэффективных операций с основной памятью:
1.2502304241761253 за 0,780 сек.
Тут следует учитывать, что даже пустой вызов контекста устройства с ожиданием занимает некоторое, у меня по крайней мере это время составило в среднем 0,26 секунды. Как бы то ни было, даже 0.52 секунды — это не тот результат, которого ожидаешь от устройства массивно-параллельной архитектуры с пиковой производительность в несколько терафлопс. Давайте попробуем сами написать ядро на CUDA C, которое выполнит предварительное суммирование. Это не так сложно… Разобъём для этого наши вычисления на блоки равной длины. Каждый блок будет проводить параллельную редукцию своих элементов в быстрой разделяемой памяти, и сохранять результат в глобальную память ускорителя, по смещению, равному индексу блока:
__global__ void SumOfSinuses(double *partial_res, int n)
{
//Размер extern-массива задаётся при старте ядра
extern __shared__ double sdata[];
//реальный индекс элемента потока
int i =blockIdx.x*blockDim.x+threadIdx.x;
sdata[threadIdx.x] = (i <= n) ? sin((double)i) : 0;
__syncthreads();
// проводим собственно редукцию элементов блока
for (int s=blockDim.x/2; s>0; s>>=1)
{
if (threadIdx.x < s)
{
sdata[threadIdx.x] += sdata[threadIdx.x + s];
}
__syncthreads();
}
// пишем частичную сумму в ячейку общей памяти, соответствующую этому блоку
if (threadIdx.x == 0) partial_res[blockIdx.x] = sdata[0];
}
Теоретически один блок может суммировать на нашем устройстве до 1024 слагаемых. После первой вызова ядра SumOfSinuses будем иметь в памяти устройства около 200 тысяч промежуточных слагаемых, которые уже спокойно можно сложить одним вызовом thrust::reduce:
int main(void)
{
int dw = GetTickCount();
int N=200000000+1;
cudaDeviceProp deviceProp;
cudaGetDeviceProperties(&deviceProp, 0);
double *partial_res;
int rest=N;int i=0;double res=0;
int threads_per_block=1024;//deviceProp.maxThreadsPerBlock;
int max_ind=deviceProp.maxGridSize[0] * threads_per_block;
checkCudaErrors(cudaMalloc(&partial_res, max_ind/threads_per_block*sizeof(double)));
thrust::device_ptr<double> arr_ptr(partial_res);
do {
int num_blocks=min((min(rest,max_ind) % threads_per_block==0) ? min(rest,max_ind)/threads_per_block : min(rest,max_ind)/threads_per_block+1,deviceProp.maxGridSize[0]);
SumOfSinuses<<<num_blocks,threads_per_block,threads_per_block*sizeof(double)>>>(partial_res,i*max_ind,N);
checkCudaErrors(cudaDeviceSynchronize());
// позволяем thrust-у увидеть наш массив и эффективно выполнить второй шаг редукции, на этот раз уже из глобальной памяти
res = thrust::reduce(arr_ptr, arr_ptr+num_blocks,res);
rest -=num_blocks*threads_per_block;
i++;
} while (rest>0);
cudaFree(partial_res);
cout.precision(20);
cout << res << endl<< "Total Time: " << (GetTickCount()-dw)<< endl;
}
1.2502304241758133 за 0,749 сек.
Цикл Do я вынужден использовать по той причине, что размер сетки блоков CUDA ограничен. Поэтому в нашем случает ядро вызывается из цикла трижды, обрабатывая каждый раз примерно по 70 миллионов слагаемых. Оказывается, всё-таки производительность упирается в вычисления трансцендентных функций с двойной точностью, так что Thrust не виноват в относительно низкой производительности, и я бы советовал использовать первый вариант, с более понятным и элегантным кодом. Кстати, наш подход пока не масштабируется по числу CUDA-совместимых устройств (из которых вполне может быть организован локальный кластер). Можно ли это исправить? Выясняется, что простое переключение контекстов между двумя устройствами и вся вспомогательная обвязка (вызов cudaSetDevice, cudaStreamCreate/cudaStreamDestroy) почему-то занимает уже около 0,5 секунды. Т.е., получается, масштабирование по нескольким CUDA-устройствам выгодно, если ядра выполняются достаточно долго, чтобы накладные расходы на переключение контекстов были незаметны. В нашем случае это не так, поэтому оставляем масштабирование по нескольким устройствам за рамками статьи (возможно, мне следовало использовать несколько потоков и на стороне хоста, не уверен).
Чуть не забыл — Matlab ведь уже года три как поддерживает выполнение кода на устройствах CUDA (разумеется, с некоторыми ограничениями). Желающие могут посмотреть англоязычный вебинар (потребуется зарегистрироваться). Объективности ради следует сказать, что в Maple поддержка CUDA рудиментарная, на уровне нескольких процедур пакета линейной алгебры. MatLab в этом плане гораздо более продвинут. Я не знаю, можно ли в текущей версии заполнять массивы последовательностями прямо на устройстве, не копируя массивы с хоста (судя по документации, нельзя). Так что применим лобовой подход:
tic;
res=0.0;n=10;stride=200000000/n;
for j=1:n
X=stride*(j-1)+1:stride*j;
A=gpuArray(X);
res=res+sum(sin(A));
end
toc;
gather(res)
1.250230424175708, Elapsed time is 2.872859 seconds.
Заставить работать код на обоих процессорах моего двухчипового ускорителя сразу не получилось, в руководствах эта тема раскрыта не полностью. Spmd работает, композитный массив, разбитый на 2 части, создаётся. Однако в определённый момент программа выходит на ошибку, сообщая, что данные больше недоступны. Кто с несколькими GPU в матлабе уже работал, отзовитесь ;-) В любом случае, матлабовская версия не будет быстрее нашей реализации в Thrust-е.
Ну что ж, хотелось бы взять fasm и добавить ещё чисто ассемблерную версию, оптимизированную с помощью событийного профилирования Vtune на предмет промахов кэша и прочих тонкостей, но уже нет сил :-) Если есть добровольцы — пожалуйста, присылайте свои результаты, с удовольствием добавлю в статью. Также было бы интересно посмотреть на результаты запуска под Knights Corner, но, к сожалению, нет подходящего железа.
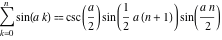
Ну или не замечать, а вбить в символьном виде формулу в Mathematica или Maple. Искомое число с 50 точными знаками после запятой:
1.2502304241756868163500362795713040947699040278200
Самая главная и наипервейшая оптимизация — всегда на уровне алгоритма :-) Тем не менее, проделанная работа не была бесполезной — ведь более сложный паттерн уже, скорее всего, не позволит применить аналитическую формулу, а как с численными задачами справляться, мы уже выяснили. Кстати, если точность суммирования важна, следует принять дополнительные меры, чтобы избежать потери значащих цифр при добавлении малых слагаемых к большой общей сумме — например, использовать алгоритм Кагана. Надеюсь, Вам было интересно!
С уважением,
Анатолий Алексеев
24.05.2013
Автор: fingoldo







//cl main.cpp /EHsc /nologo /O2 /arch:SSE2 /openmp
#include
#include
using namespace std;
int main()
{
double res=0.0;
int dw = GetTickCount();
#pragma omp parallel for reduction(+:res)
for (int i = 1; i <= 200000000; i++)
res+=sin(double(i));
cout.precision(20);
cout << "Result: " << res << " after " << (GetTickCount()-dw);
}