На сколько еще необходимо продлить самоизоляцию в стране и регионах, чтобы в конечном итоге не переболел каждый первый, применять ли жесткие санкции к нарушителям самоизоляции, призывать ли к усилению мер предосторожности или оставить большую часть населения с искренней верой в полезность медицинских масок?
Для получения ответов хотя бы на часть вопросов, в данной статье будет проведен анализ модели SIR из нашумевшего видео с ютуба и основанных на ней симуляций различных эпидемиологических ситуаций, а также качественное сравнение влияния тех или иных факторов на скорость и масштаб распространения инфекции.
Кроме того, в дальнейших постах будут исследованы более сложные модели, описывающих динамику распространения вируса COVID-19.
Минутка заботы от НЛО
В мире официально объявлена пандемия COVID-19 — потенциально тяжёлой острой респираторной инфекции, вызываемой коронавирусом SARS-CoV-2 (2019-nCoV). На Хабре много информации по этой теме — всегда помните о том, что она может быть как достоверной/полезной, так и наоборот.
Мы призываем вас критично относиться к любой публикуемой информации
Официальные источники
- Cайт Министерства здравоохранения РФ
- Cайт Роспотребнадзора
- Сайт ВОЗ (англ)
- Сайт ВОЗ
- Сайты и официальные группы оперативных штабов в регионах
Если вы проживаете не в России, обратитесь к аналогичным сайтам вашей страны.
Мойте руки, берегите близких, по возможности оставайтесь дома и работайте удалённо.
Читать публикации про: коронавирус | удалённую работу
Краткое описание модели
Итак, представим, что мы наблюдаем за некоторым закрытым городом, где на постоянной основе проживает N жителей, которые никуда не выезжают и не принимают у себя иногородних гостей, но внутри своего города достаточно социально активны.
То есть мы наблюдаем за связным замкнутым сообществом (или системой). В какой-то момент в этой системе появляется человек, зараженный COVID-19, и вот, мы уже делим всех жителей нашего сообщества на три потенциально возможные группы:
- S (Susceptible) — уязвимые (могут заразиться),
- I (Infected) — инфицированные (те, кому не повезло),
- R (Removed) — выбывшие, которые также делятся на две подгруппы:
- Recovered — выздоровевшие и получившие иммунитет (те, кому сначала не повезло, а потом повезло)
- Dead — умершие (те, кому сначала не повезло… и потом не повезло).


Каждый день из рассматриваемого периода мы можем считать, сколько человек попало в каждую из трех групп, получив таким образом функции 



Наша задача — предугадать динамику распространения инфекции в нашей системе, в зависимости от заданных значений многочисленных факторов влияния. По сути, мы хотим предсказывать скорость и динамику изменения наших трех получившихся функций. В этом нам помогут дифференциальные уравнения с параметрами, соответствующими этим факторам влияния. Таким образом, мы получаем базовую модель SIR, которая представляет из себя систему дифференциальных уравнений первого порядка.
Стоит отметить, что граничные значения параметров брались для пессимистичного и оптимистичного сценариев, а промежуточные согласно статистике по России и Нижегородской области. Но это никак не влияет на качественные результаты, которые можно обобщить для всех регионов и страны в целом.
Фиксированные параметры модели:
- Доля смертности из общего числа выбывших (Dead/Removed) — 12% (согласно уровню смертности по России). В данной модели не учитывается повышение доли смертности при перегрузке системы здравоохранения.
- Введение карантина для подтвержденных больных после 50 случаев заражения (во время карантина больных изолируют на следующий день после заражения).
- Введение домашней изоляции после 50 случаев заражения.
- Вероятность повторного заражения равна нулю (у ученых нет единого мнения на этот счет, но сделаем такое допущение для упрощения модели).
Исследуемые параметры модели:
- CP (contagion probability) — вероятность заражения при контакте с инфицированным: 30% — выбирается как опорный показатель, на котором построены большинство моделей (согласно мнению эпидемиологов), рассмотрены также 20% и 10%.
- SD (social distance) — вероятность соблюдения домашней изоляции каждым человеком. В видео заражение описывается через физический контакт, у каждой точки есть радиус заражения. Когда мы включаем SD — срабатывает запрет точке приближаться к другим на расстояние в несколько раз превышающее радиус заражения. Однако, точка может нарушить этот запрет с вероятностью равной параметру 100-SD.
В крайнем приближении SD соответствует домашней изоляции, которая соблюдается с некоторой вероятностью. Чем меньше этот параметр, тем больше людей перемещается по городу. Для него рассматриваются следующие значения: 10%, 40%*, 75%*, 90%. - IP (isolation period) — длительность домашней изоляции в днях. Берутся значения: 30 (апрельский карантин), 45 (отмена изоляции после майских праздников), 70 (продление карантина до лета), и изоляция в неограниченное число дней.
- AC (asymptomatic cases) — доля невыявленных** случаев заболевания — 5% (при условии массового тестирования), 40% (согласно российской статистике), 70% (согласно итальянской статистике).
- DT (disease time) — время болезни 14 (длительность официального карантина), 21 (согласно российским эпидемиологам), 38 дней (максимально зарегистрированное).
* согласно индексу самоизоляции Яндекса по Нижегородской области в разные периоды
** в модели тестирование не проводится, поэтому невыявленные случаи эквивалентны бессимптомным носителям
При изменении одного параметра значения остальных устанавливались следующими: CP=30% (согласно эпидемиологам), SD=75% (по индексу самоизоляции Яндекса), IP=unlimited (для более точной оценки рассматриваемого параметра), AC=40% (согласно эпидемиологам), DT=21 (согласно эпидемиологам). Желтые вертикальные линии — начало и конец домашней изоляции.
Исследование параметров модели
-
Вероятность заражения CP
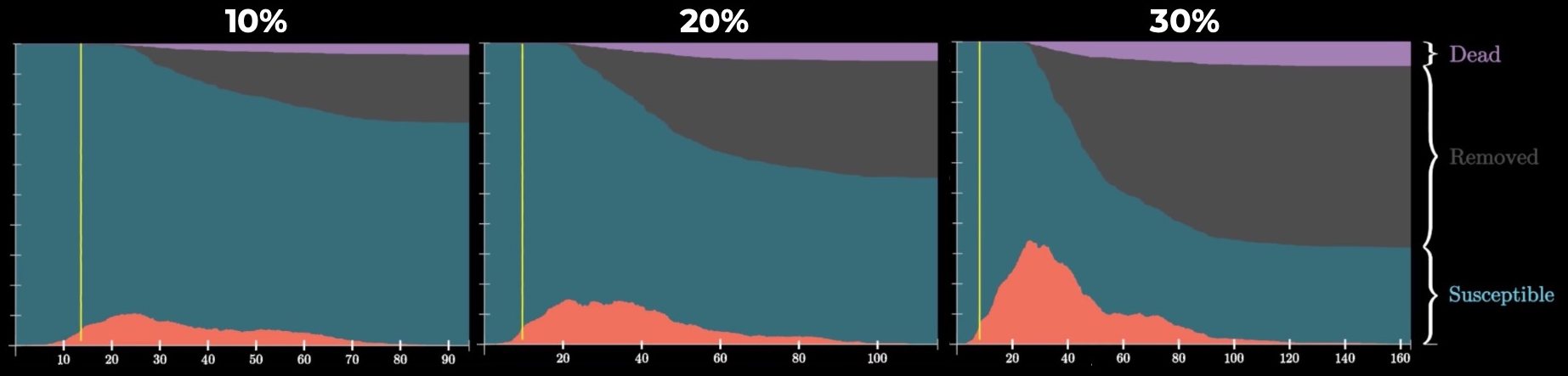
Никаких сюрпризов — чем больше вероятность заболеть, тем больше людей заболевают (и тем длиннее эпидемия!). Эту вероятность можно снизить мерами предосторожности (ношение респиратора, перчаток, соблюдение дистанции) и особым вниманием к гигиене.
Качественно развитие пандемии в мире больше всего похоже на третий график, именно его поддерживают эпидемиологи, поэтому данное значение 30% будет использоваться в дальнейших симуляциях.
-
Посмотрим, как влияет на распространение вируса вероятность соблюдения домашней изоляции SD
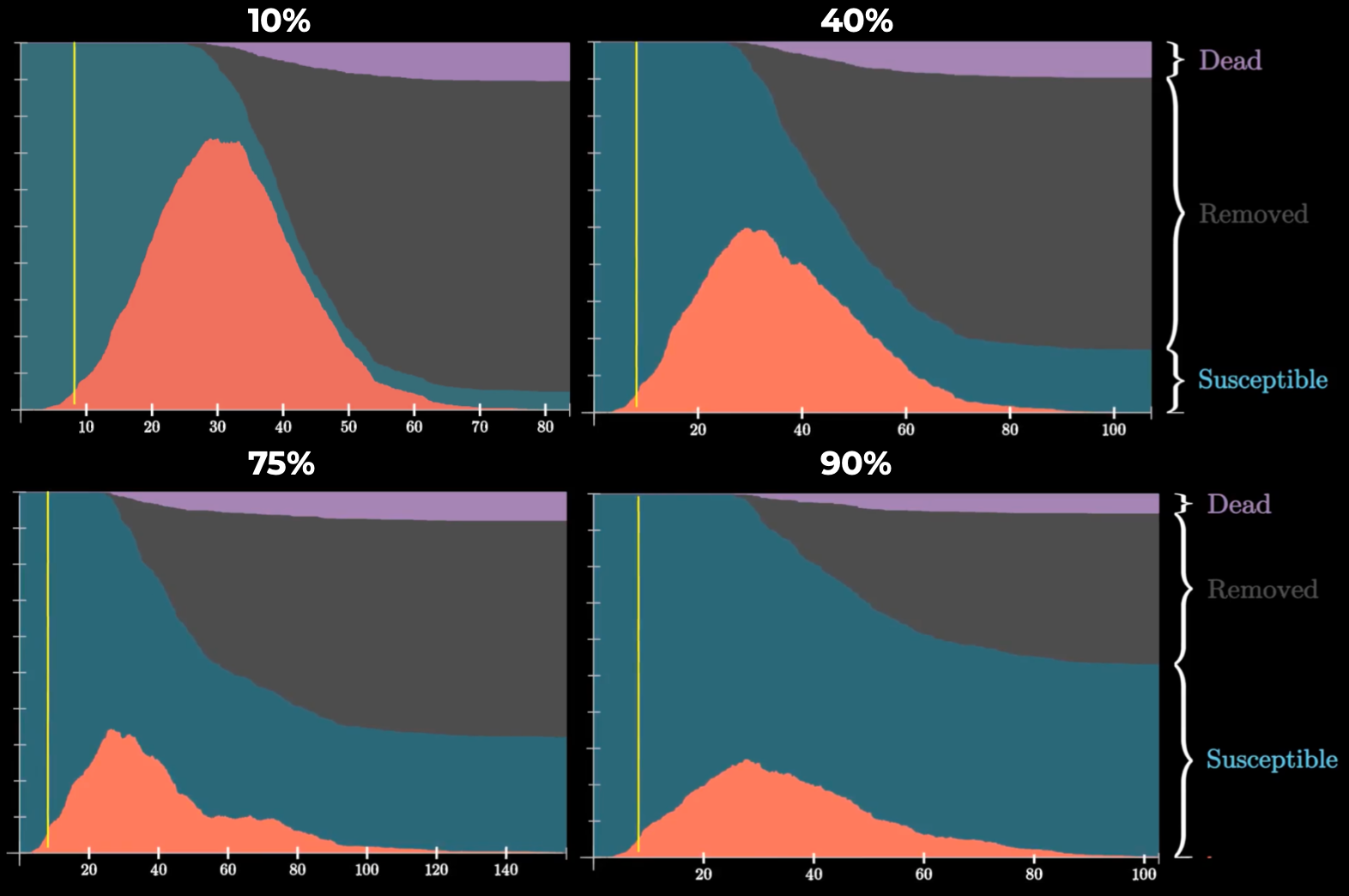
Несоблюдение самоизоляции влияет на скорость распространения эпидемии и ее длительность. Чем лучше люди соблюдают домашнюю изоляцию, тем меньше людей в итоге переболеет. Когда изоляция соблюдается с вероятностью лишь 10%, количество болеющих одновременно более, чем в два раза превышает тот же показатель при вероятности соблюдения 90%. Следовательно, чем меньше мы соблюдаем самоизоляцию, тем больше нагрузка на систему здравоохранения.
-
Теперь рассмотрим влияние длительности домашней изоляции IP
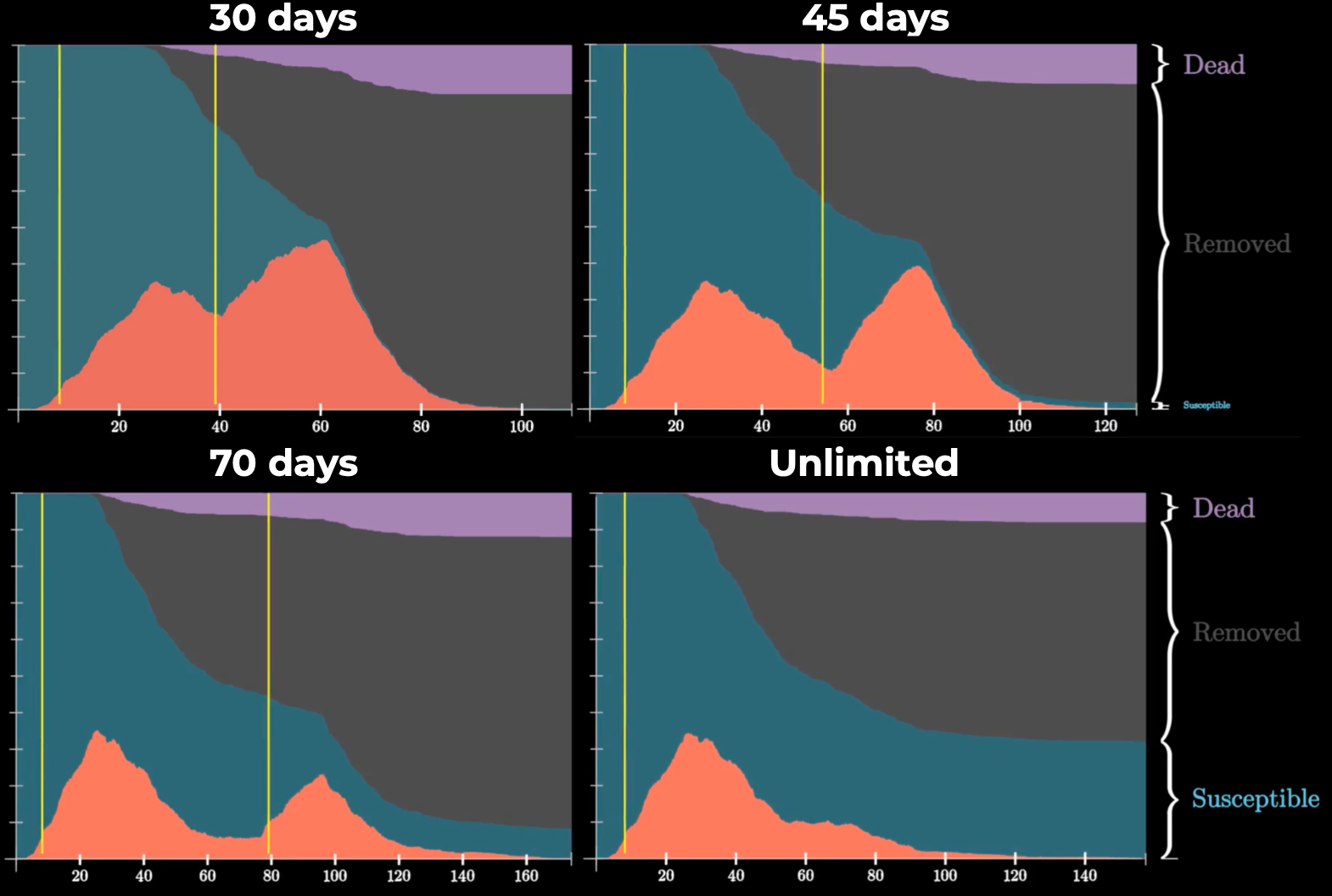
Видео: 30 дней, 45 дней, 70 дней, неограниченная домашняя изоляция
При уменьшении срока карантина вероятность появления и "мощность" второй волны существенно повышаются. Вторая вспышка может быть даже значительнее первой по общему количеству заболевших и умерших. Кроме того, вторая волна создает дополнительную нагрузку на систему здравоохранения.
-
Влияние доли бессимптомных носителей на динамику эпидемии AC

График, когда доля бессимптомных носителей 5%, эквивалентен массовому тестированию людей, так как подтвержденные случаи отправляются на карантин и больше не разносят инфекцию. А 70%, наоборот, — малому проценту тестирования.
Масштаб тестирования людей оказывает большое влияние на количество заболевших и длительность эпидемии, поскольку реальная доля бессимптомных носителей COVID-19 точно неизвестна и может варьироваться в значительных пределах.
Оптимально тестировать в первую очередь тех людей из группы риска, которые не имеют возможность соблюдать домашнюю изоляцию: работников продуктовых магазинов, аптек, непрерывно работающих предприятий и так далее.
-
Среднее время протекания самой болезни на распространение коронавируса DT
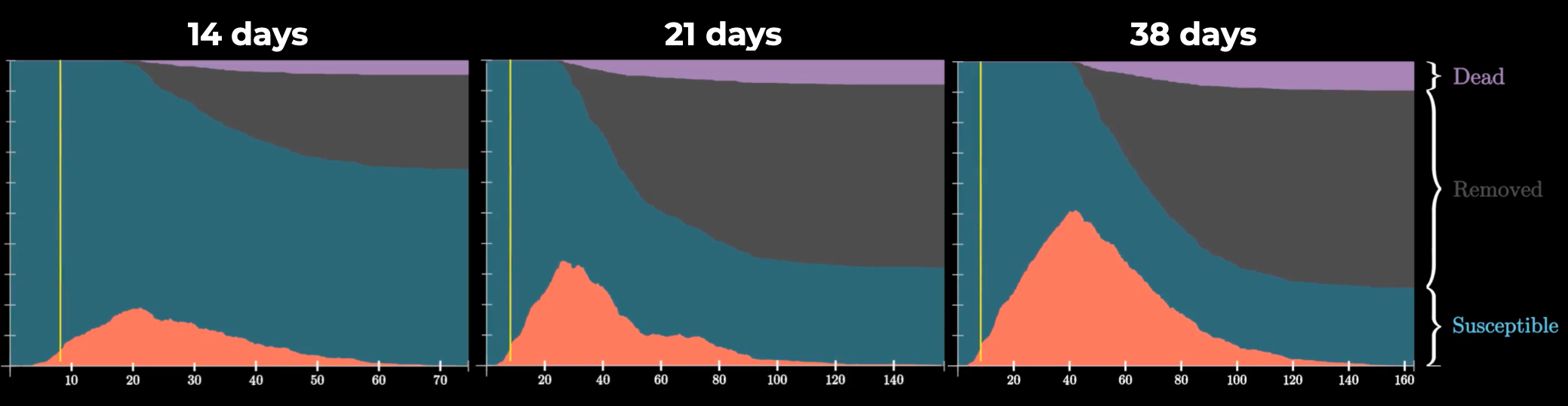
Видео: 14 дней, 21 день, 38 дней
Хоть мы и не можем прямо влиять на этот фактор, но мы должны учитывать его в дальнейшем. От времени болезни зависит длительность эпидемии, скорость ее распространения и количество заболевших и, опираясь на этот фактор, стоит корректировать длительность домашней изоляции.
Центры скопления людей во время эпидемии
Кроме вышеописанных параметров и соответствующих факторов влияния, можно также исследовать и моделировать единичные случаи поведения нашего замкнутого сообщества, которые напрямую не зависят от параметров модели.
Одним из таких случаев является посещение большой долей населения так называемых "центров притяжения" (митинги, храмы, предприятия, торговые центры), где один инфицированный человек может поспособствовать быстрому и масштабному распространению инфекции по всей системе.
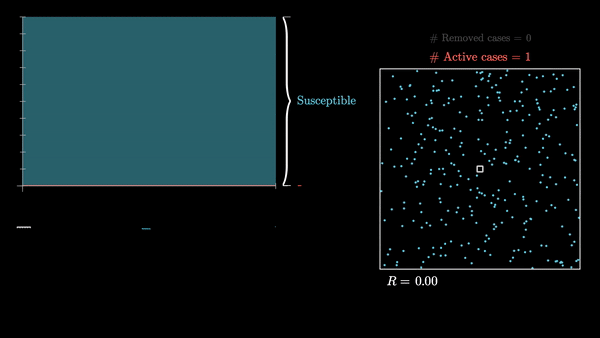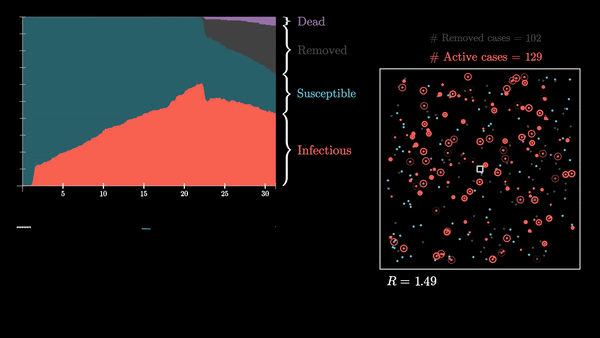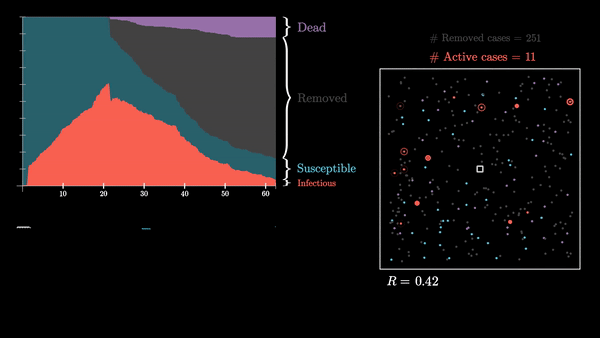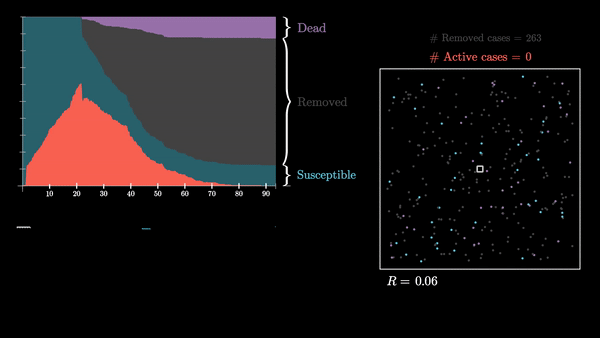
Эпидемия развивается стремительно, заболевает большой процент сообщества. Последний заболевший человек выздоравливает примерно через 90 дней после начала эпидемии.

В воскресенье 8 марта тысячи женщин по всей Испании провели марш против гендерного неравенства, чтобы отметить Международный женский день, несмотря на опасения, что собрания могут помочь распространению коронавируса.
Ряд событий был отменен или отложен в Испании, чтобы минимизировать возможность распространения коронавируса, но координатор по чрезвычайным ситуациям в области здравоохранения Фернандо Симон заявил, что министерство здравоохранения не считает марши риском.
В начале эпидемии власти Южной Кореи сообщили, что сторонники апокалиптической секты ответственны почти за половину всех случаев заражения в стране. На тот момент из 100 новых заболевших 86 находились в городе Тэгу, причем практически все они принадлежали к данной секте. Предполагается, что вспышка заболеваний в Южной Корее началась с города, где большое количество членов секты с 31 января по 2 февраля посетили отпевании и похороны одного из братьев-основателей, а источником заражения стала 61-летняя женщина, у которой был выявлен коронавирус.
К сожалению, даже спустя столько времени и усилий по предотвращению распространения эпидемии, в нашей стране, в том числе и в нашем регионе, нередки случаи проявления безответственного отношения людей к данной проблеме.

Так, 12 апреля, жители Нижегородской области проигнорировали призыв патриарха Кирилла молиться дома и посетили Свято-Троицкий Серафимо-Дивеевский монастырь. Многие из прихожан были вместе с детьми и ни о какой дистанции между людьми речи не идёт. Почти все были без средств защиты.
Мы ни в коем случае не проводим параллель между корейской религиозной сектой и российской православной церковью. Лишь призываем людей в сложившейся ситуации к сознательным и обдуманным поступкам, которые будут способствовать скорейшему ослаблению распространения вируса.

Житель ЖК «Бутово парк 2» в Подмосковье организовал «балконную дискотеку», чтобы развлечь своих соседей во время режима самоизоляции, однако впоследствии люди продолжили вечеринку на улице
Конечно, эта простая модель не учитывает ряд факторов влияния на эпидемию, как контролируемых людьми, так и зависящих лишь от природы самого вируса, и не всегда точно переносится на реальность. Однако, свою функцию она выполняет — дает качественную оценку основным механизмам, воздействующим на динамику эпидемии, и наглядно демонстрирует это воздействие.
Полезные материалы
Отдельная благодарность pixml и keysloss за помощь в написании статьи и подготовке симуляций.
Автор: stasysp