Автоматные рекурсивные вычисления

1. Введение

Влияние подпрограмм (англ. subroutine) на программирование без преувеличения огромно. Введенные на заре программирования они не теряют своей актуальности и поныне. Без них практическое программирование представить просто невозможно. Хотя с формальной точки зрения они не так уж и нужны, т.к. чистую теорию интересуют больше свойства алгоритма, чем его размеры.

В теории автоматов понятие вложенных автоматов, на базе которых строилась бы практика автоматных подпрограмм (АПП), обсуждается редко. Подобная (вложенная) иерархическая организация автоматов, если и рассматривается, то весьма поверхностно. Одной из причин подобного отношения может служить сложность реализации вложенной иерархии на аппаратном уровне [1, 2].

Программирование более гибко и предоставляет больше возможностей, чем практика проектирования цифровых схем. В этом нам предстоит убедиться, рассматривая далее программную реализацию вложенных автоматов, а следом и концепцию автоматных рекурсивных алгоритмов.

При всех частных проблемах формирования вложенной автоматной модели ее формальное определение не вызывает каких-то проблем. Но, с другой стороны, выбор построения иерархии модели, безусловно, будет оказывать существенное влияние на ее программную реализацию.

2. Автоматные рекурсивные алгоритмы

В предыдущей статье [3] было дано только формальное определение модели управления автоматных программ (АП) без рассмотрения ее реализации и конкретных примеров использования. Была упомянута и возможность реализации рекурсивных алгоритмов. Далее на примере вычисления факториала мы, во-первых, рассмотрим программную реализацию механизмов создания автоматных подпрограмм в рамках объектной парадигмы «автоматного С++», а, во-вторых, поскольку будем рассматривать рекурсивный алгоритм, то определим по сути общий принцип реализации любых подобных алгоритмов в рамках автоматного программирования.

Использование рекурсивных функций в АП может быть совсем простым. Это демонстрирует код листинга 1 объектной автоматной программы. Здесь автоматный класс FSimpleFactorial не процесс, а автоматная подпрограмма, т.к. содержит заключительное состояние «00» (подробнее о подпрограммах см. [3]). На уровне поведения созданному автоматному объекту соответствует автомат с одним безусловным переходом из начального состояния «f0» в заключительное состояние «00» и вызовом на этом переходе в рамках действия y1 обычной функции вычисления факториала factorial(...).

#include "lfsaappl.h"

class FSimpleFactorial : public LFsaAppl
{
public:
    double dF{1};		//	значение факториала
    FSimpleFactorial(int n);
    virtual ~FSimpleFactorial() {};
private:
    int nN{0};
    void y1();
    double factorial(int n);
};

#include "stdafx.h"
#include "FSimpleFactorial.h"

LArc TT_SimpleFactorial[] = {
    LArc("f0", "00", "--",	"y1"),		//
    LArc()
};
//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////
FSimpleFactorial::FSimpleFactorial(int n)
    :LFsaAppl(TT_SimpleFactorial, "FSimpleFactorial")
{
    nN = n;
}
//
void FSimpleFactorial::y1() { dF = factorial(nN); }

double FSimpleFactorial::factorial(int n)
{
    if (n == 0) return 1;
    else return n*factorial(n-1);
}

Поскольку объект FSimpleFactorial вложенный автомат (подпрограмма), то для него должна быть «обертка» — процесс, который его вызывает. Его пример — процесс, порожденный от объекта с именем FTskSimple, код которого приведен в листинге 2.

#include "lfsaappl.h"

class FTskSimple : public LFsaAppl
{
public:
    LFsaAppl* Create(CVarFSA *pCVF) { Q_UNUSED(pCVF)return new FTskSimple(nameFsa); }
    bool FCreationOfLinksForVariables();
    FTskSimple(string strNam);
    virtual ~FTskSimple();

    CVar    *pVarF;
    CVar    *pVarN;
    CVar    *pVarStart;

    LFsaAppl *pFCall{nullptr};
protected:
    int x1();
    void y1(); void y2(); void y3();
};

#include "stdafx.h"
#include "FTskSimple.h"
#include "FSimpleFactorial.h"
//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////
LArc TT_Task[] = {
    LArc("st", "t1", "--",	"y1"),	//
    LArc("t1", "t2", "x1",	"y3"),	//
    LArc("t2", "t1", "--",	"y2"),	//
    };

FTskSimple::FTskSimple(string strNam)
    :LFsaAppl(TT_Task, strNam)
{
}

FTskSimple::~FTskSimple() { if (pFCall) delete pFCall; }

bool FTskSimple::FCreationOfLinksForVariables() {
    pVarF = CreateLocVar("dF", CLocVar::vtDouble, "factorial value");
    pVarN = CreateLocVar("nN", CLocVar::vtInteger, "input value");
    pVarStart = CreateLocVar("bStart", CLocVar::vtBool, "start?");
    return true;
}

int FTskSimple::x1() { return pVarStart->GetDataSrc(); }

void FTskSimple::y1()
{
    // reset flag start
    pVarStart->SetDataSrc(this, 0.0);
    // creating and calling a subroutine
    pFCall = new FSimpleFactorial(pVarN->GetDataSrc());
}
void FTskSimple::y2()
{
    // display factorial value
    pVarF->SetDataSrc(this, static_cast<FSimpleFactorial*>(pFCall)->dF);
}

void FTskSimple::y3()
{
    // reset flag start
    pVarStart->SetDataSrc(this, 0.0);
    static_cast<FSimpleFactorial*>(pFCall)->nN = pVarN->GetDataSrc();
    // creating and calling a subroutine
    pFCall->FCall(this);
}

Данный процесс на переходе из начального состояния «st» в состояние «t1» создает объект типа FSimpleFactorial, который будет основой для создания вложенного автомата (в обычном понимании — вызова подпрограммы). Далее он, исходя из текущего состояния локальной переменной булевского типа bStart (см. также код предиката x1), вызывает переход из состояния «t1» в «t2». На этом переходе действие y1, во-первых, сбрасывает значение данной локальной переменной (чтобы исключить ложный повторный запуск) и, во-вторых, вызывает процедуру FCall, которая создает вложенный автомат.

Интерпретатор автоматов среды ВКПа организует переход в начальное состояние «f0» вложенного автомата и состояния последнего становятся текущими состояниями процесса. Переход вложенного автомата в заключительное состояние «00» возвращает вычисления на предыдущий уровень вложенности, а в нашем случае и к завершению перехода автомата верхнего уровня в состояние t2. Затем процесс на безусловном переходе из состояния «t2» в состояние «t1» выполняет действие y2, которое устанавливает результат вычисления факториала локальной переменной процесса dF.

Отметим, а это очень важно, что результат вложенного автомата будет доступен только после завершения его работы и перехода в следующее состояние автомата верхнего уровня. Получить его (результат) можно будет через указатель на объект вложенного автомата.

И все было бы хорошо, если бы не время работы рекурсивных функций. По сравнению с обычной подпрограммой оно в силу вложенности, как правило, много больше и потому может нарушать условную атомарность действий автоматных процессов, суммарное время исполнения действий которых должно укладываться в значение дискретного такта.

В нашем случае вычисление факториала достаточно мало и вплоть до максимальной величины результата типа double для n = 170 укладывается в 1 мксек. Для вычисления больших значений нужно переходить уже на длинную арифметику (см. например, [4, 5]). При этом время вычисления факториала еще больше увеличится и почти гарантированно выйдет за пределы дискретного такта, повлияв на скорость работы остальных автоматов сети, работающих в режиме невытесняющей многозадачности, и на реактивность отклика приложения в целом, которое проявится в его «тормозах».

Уложиться в дискретный такт и избавиться от дефекта «тормозов» можно, разложив вычисление на шаги. В этих целях удобно перевести обычный алгоритм вычисления факториала в автоматную форму. Правда, из-за режима интерпретации автоматов время вычисления увеличится, но зато временные свойства приложения придут в норму.

На листинге 3 приведено вычисление факториала в обычном виде и в виде, подготовленном для последующего преобразования в автоматную форму. Последний в явной форме представляет атомарные шаги, которые скрыты в исходном тексте программы. Речь в данном случае идет об операторах вида y = f(...), где f — обычная или рекурсивная программная функция. Подобная запись маскирует время работы функции и создает ложное впечатление о «мгновенности» присваивания значения переменной y. В реальности нет ни того, ни другого.

int factorial(int n)
{
    if (n == 0) return 1;
    else return n*factorial(n-1);
}

double Factorial(int n)
{
    double dF = 1;
    if (n == 0)
        return dF;
    else {
        double dPrev = Factorial(n-1);
        double dF = n*dPrev;
        return dF;
    }
}

В рамках концепции автоматного программирования атомарные действия (методы) программных автоматных объектов считаются условно мгновенными. И если только суммарное время работы действий укладывается в единичный такт дискретного времени автоматного пространства, то тогда программная реализация соответствует своей формальной модели.

Замечание 1. Суммарное реальное время работы действий на том или ином дискретном такте может разниться достаточно сильно. Среда ВКПа в случае превышения длительности такта пытается на последующих тактах работы автоматного пространства компенсировать его, уменьшая, если это возможно, дискретное время последующих тактов.

На рис. 1 приведена блок-схема, которая включает разметку, отражающую состояния эквивалентного конечного автомата и имена его предикатов и действий. Сама автоматная модель в форме графа автомата приведена на рис. 2.

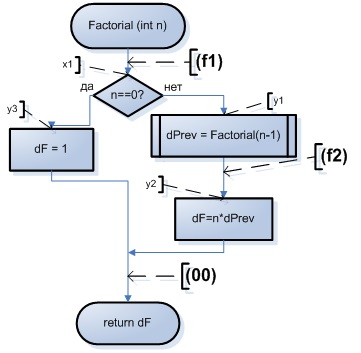
Рис. 1. Блок-схема рекурсивного алгоритма вычисления факториала

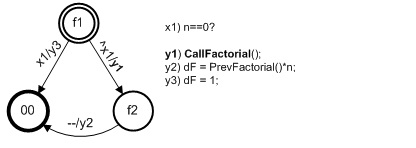
Рис. 2. Автоматная модель рекурсивного алгоритма вычисления факториала

Код автоматной подпрограммы вычисления факториала демонстрирует листинг 4. Комментарии в таблице переходов (ТП) отражают время вычисления факториала в мсек и количество дискретных шагов, затраченных на процедуру вычисления для n=170. И если время вычислений завит от быстродействия вычислительной платформы и/или от типа проекта (debug/release), то количество дискретных шагов (тактов автомата) определяется только свойствами алгоритма и может служить объективной оценкой быстродействия алгоритма уже вне зависимости от формы его представления и реализации.

В случае автоматной модели число дискретных тактов можно подсчитать достаточно просто и, набрав определенную статистику, вывести аналитическую формулу быстродействия алгоритма. Пока же такие оценки весьма приблизительны и базируются на выводах, полученных часто в результате достаточно сложных рассуждений.

#include "lfsaappl.h"

class FFactRec : public LFsaAppl
{
public:
    FFactRec(int n);
    virtual ~FFactRec() { if (pFFactRec) delete pFFactRec; };
    int nN;		//	n
    double dF;	//	n!
private:
	int x1();
    void y1(); void y2(); void y3();
protected:
    void CallFactorial();
    double  PrevFactorial();
    FFactRec *pFFactRec{nullptr};
};

#include "stdafx.h"
#include "FFactRec.h"

#define QT_NO_DEBUG_OUTPUT

extern LArc TT_FactRec[];
//////////////////////////////////////////////////////////////////////
// Construction/Destruction
//////////////////////////////////////////////////////////////////////
//	объектная рекурсивная автоматная модель
FFactRec::FFactRec(int n)
    :LFsaAppl(TT_FactRec, "FFactRec")
{
    nN=n; dF=1;
}

LArc TT_FactRec[] = {
//        Debug    Release     Steps
//msec: 120-129   98-101        340
    LArc("f1", "00", "x1",	"y3"),	//
    LArc("f1", "f2", "^x1",	"y1"),	//
    LArc("f2", "00", "--",	"y2"),	//
    LArc()
};

int FFactRec::x1() { return nN==0; }
// рекурсивный вызов функции
void FFactRec::y1() { CallFactorial(); }
//	1. взять значение от предыдущего уровня рекурсии
//	2. вычислить текущее значение факториала
void FFactRec::y2() { dF = PrevFactorial()*nN; }
// 0!
void FFactRec::y3() { dF = 1; }
// Вызов подпрограммы (создание вложенного автомата)
void FFactRec::CallFactorial()	{
    //	удалить из стека предыдущий рекурсивный объект
    pFFactRec = new FFactRec(nN-1);
    pFFactRec->FCall(this);
};
// взять значение вложенного автомата
double  FFactRec::PrevFactorial()	{ return pFFactRec->dF; };

3. Выводы

Признаюсь, в силу специфики решаемых задач мне фактически не пришлось в реальных проектах использовать, да и разрабатывать рекурсивные алгоритмы, кроме как в учебных целях и для тестировании ядра на реализацию вложенности. Автоматные подпрограммы — почти постоянно и большом количестве. Среди них особенно интересны подпрограммы, названные инерционными (подробнее о них см. в [3]). Но их рассмотрению предполагается посвятить отдельную статью.

Рекурсивные алгоритмы — важная часть теории программ [6]. Без реализации подпрограмм и рекурсии сложно представить эффективную и удобную со всех точек зрения вычислительную модель. А реализовать рекурсию, учитывая возможности объектного программирования (см. примеры статьи), после создания модели подпрограмм, не так уж и сложно. Можно, конечно, используя те или иные методы преобразования рекурсии в обычную форму, обойти ее, используя те же циклы. Но предпочтительнее не избавляться тупо от нее, а иметь прямые механизмы ее реализации. Конечно, будет медленнее, конечно, накладнее по ресурсам (расходам той же стековой памяти), но при существующих аппаратных возможностях это не будет так уж критично.

Но рекурсивные алгоритмы интересны еще и в качестве тестов оценки возможностей, универсальности и эффективности алгоритмических моделей. В этом смысле автоматная модель не только достаточно эффективно реализует рекурсию, но и бонусом добавляет «автоматные фишки» — возможность контроля внутреннего состояния рекурсивного алгоритма, подсчета шагов для оценки быстродействия, управление временем исполнения алгоритма и т.д. и т.п.

Бороться с рекурсией достаточно бессмысленно. Ее нужно уметь использовать. Приведу цитату, с которой я согласен полностью: «На первый взгляд рекурсия может показаться сложной. Но в некоторых случаях, рекурсивный метод невероятно эффективен, если всё сделать правильно. Тем не менее, иногда лучше использовать циклы. Понимание обоих методов и умение эффективно их использовать поможет вам в работе и будет преимуществом на собеседовании» [7]. От себя могу лишь еще добавить, что автоматные модели рекурсивных алгоритмов позволяют, используя «автоматные свойства» вычислительной модели, понять рекурсию, отладить и доработать подобный алгоритм много быстрее.

И последнее. Хочется все же получить ответ на вопрос — как дела с рекурсией у корутин? Я уже задавал его, но ответа так и не получил… Ведь, одно дело создать миллион корутин (примеры этого см. [8]) и другое — реализовать рекурсивный алгоритм, имеющий пусть не такой же, но достаточно большой ранг вложенности. И, похоже, ответ на этот вопрос интересует не только меня одного… [9]

Автор: Вячеслав Любченко

Источник