Если вы следили за моей серией постов «Растеризация за одни выходные», но не компилировали и не запускали демо, то для вас станет большим сюрпризом, если я скажу, насколько медленными они оказались. В конце серии постов я упомянул существующие техники, позволяющие ускорить мучительно тормозной растеризатор. Теперь настало время двигаться дальше и посмотреть, как они применяются на практике.
Как часть этого проекта я реализовал Tyler — тайловый растеризатор, который мы проанализируем в данной статье. Моей целью при разработке этого проекта были масштабируемость. настраиваемость и понятность растеризатора для людей, которые хотят немного больше понять в этой теме и поэкспериментировать с ней. Эта статья достаточно сильно связана с тем, что объяснено в серии «Растеризация за одни выходные», поэтому лучше будет прочитать и её. Я не буду предполагать, что вы её изучили, но в статье будет больше высокоуровневых объяснений — я не хочу повторять уже сказанное и то, что можно найти в других источниках.
Краткий обзор
Тайловый рендеринг (tile-based rendering или tiled rendering) — это улучшенный по сравнению с традиционным immediate-mode-рендерингом; в нём render target (RT) разделяется на тайлы (т.е. субрегионы кадрового буфера), каждый из которых содержит примитивы, которые можно рендерить в тайлы по отдельности.
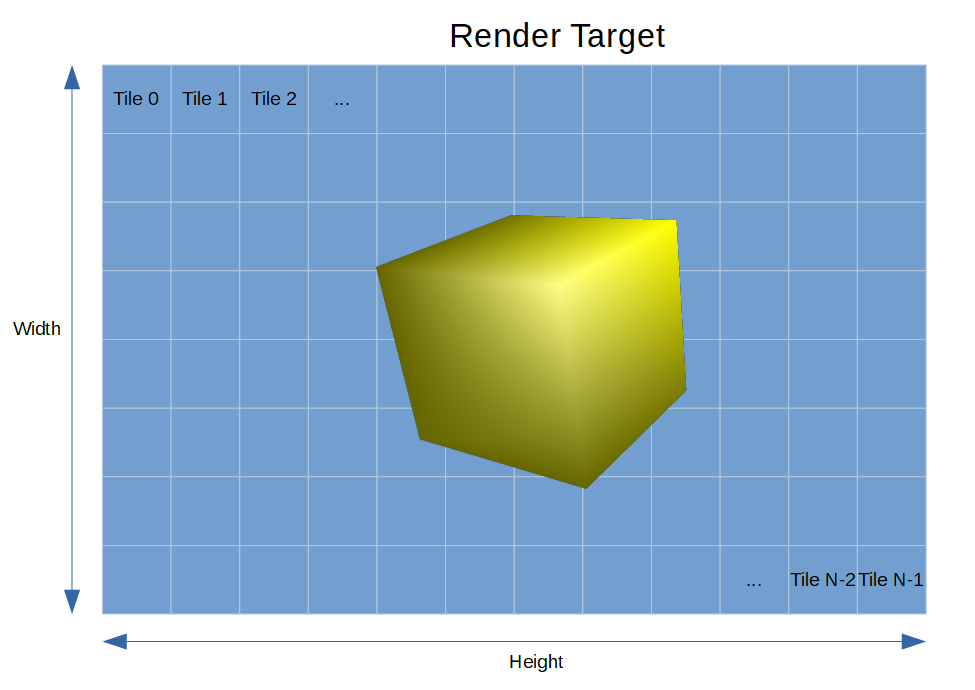
Обратите внимание на выражение «по отдельности», потому что оно подчёркивает одно из самых больших преимуществ этой техники по сравнению с immediate-mode: ограничение всех операций доступа внутри тайла буферами цветов/глубин, которые остаются в «медленной» DRAM благодаря использованию отдельного тайлового кэша на чипе. Разумеется, эта экономящая пропускную способность технология в основном используется на мобильных маломощных GPU. Посмотрите на рисунок ниже: в верхней части вершины обрабатываются, растеризируются и затеняются сразу же, а в нижней части операции отложены.
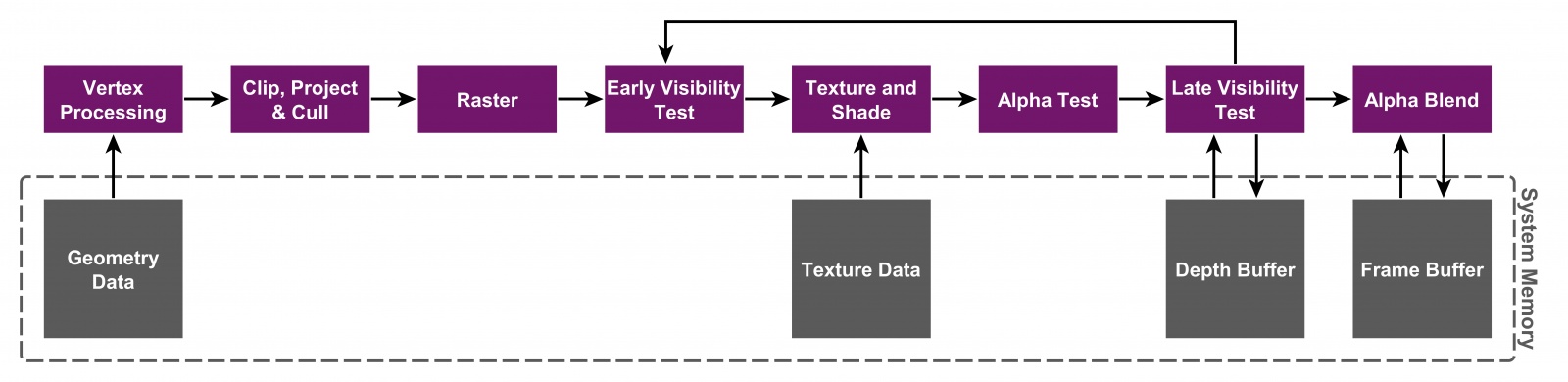
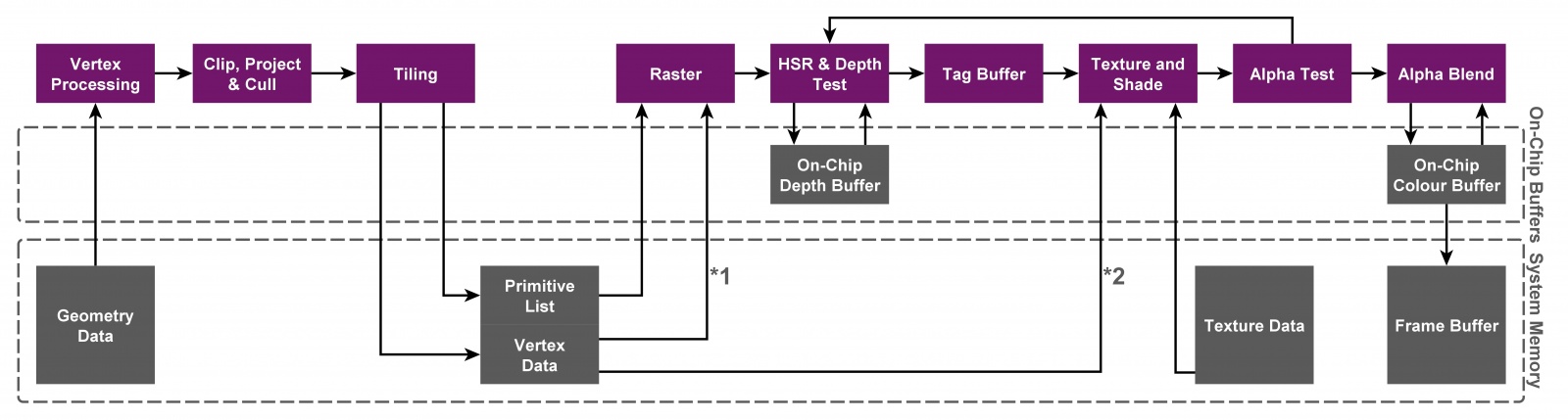
Сравнение архитектур Immediate-mode и Tile-based (PowerVR)
На высоком уровне для работы тайлового рендеринга в дополнение к обычной механике растеризатора достаточно построить для каждого тайла список примитивов, которые накладываются на данный тайл, а затем затенить все примитивы во всех тайлах по одному или, что даже лучше, параллельно. Разумеется, в таком описании теряются детали, поэтому ниже мы подробно рассмотрим реализацию Tyler.
Этот растеризатор реализует только небольшое подмножество современного конвейера 3D-рендеринга и состоит из следующих этапов, которые проходят треугольники, от вершинных буферов до пикселей на экране:
- Вершинный шейдер
- Clipper (только для полных треугольников!)
- Подготовка и усечение треугольников
- Группировщик
- Растеризатор
- Фрагментный шейдер
Tyler имеет псевдо-API для рендеринга, имитирующий поведение настоящего графического API, поэтому давайте сначала рассмотрим, как его можно использовать для настройки растеризатора и отправки вызовов отрисовки. Заметьте, что в основном я ссылаюсь на пример Scene Rendering, который загружает файл сцены .OBJ и рендерит несколько мешей, визуализирующих для простоты масштабированные нормали и опционально представляющый сцену в окне.
Подготовка контекста растеризатора
// Create and initialize the rasterizer rendering context
RenderContext* pRenderContext = new RenderContext(config);
pRenderContext->Initialize()
// Allocate color & depth buffers
uint8_t* pColorBuffer = ... // Color buffer format == R8G8B8A8_UNORM
float* pDepthBuffer = ... // Depth buffer format == D32_FLOAT
// Set up main FBO
Framebuffer fbo = {};
fbo.m_pColorBuffer = pColorBuffer;
fbo.m_pDepthBuffer = pDepthBuffer;
fbo.m_Width = opt.m_ScreenWidth;
fbo.m_Height = opt.m_ScreenHeight;
// Single vec3 attribute is used to pass vertex normal VS -> FS
ShaderMetadata metadata = { 0, 1 /*vertex normal*/, 0 };
// Emulate passing of constants data to shaders
Constants cb;
cb.m_ModelViewProj = proj * view * model;
// We will have single index and vertex buffer to draw indexed mesh
std::vector<Vertex> vertexBuffer;
std::vector<uint32_t> indexBuffer;
// Store data of all scene objects to be drawn
std::vector<Mesh> objects;
// Load .OBJ scene model data and generate vertex/index buffers, etc.
InitializeSceneObjects(opt.m_OBJName, objects, vertexBuffer, indexBuffer);
// Bind FBO to be used in subsequent render pass once
pRenderContext->BindFramebuffer(&fbo);
// Bind VBO and set buffer stride
pRenderContext->BindVertexBuffer(vertexBuffer.data(), sizeof(Vertex));
// Bind IBO
pRenderContext->BindIndexBuffer(indexBuffer.data());
// Bind shader constants
pRenderContext->BindConstantBuffer(&cb);
// Bind shader, constant buffer, texture(s)
pRenderContext->BindShaders(VS, FS, metadata);Основной цикл рендеринга
// Clear RT
pRenderContext->BeginRenderPass(
true, /*clearColor*/
glm::vec4(0, 0, 0, 1) /*colorValue*/,
true, /*clearDepth*/
FLT_MAX /*depthValue*/);
// Draw meshes
for (uint32_t obj = 0; obj < objects.size(); obj++)
{
Mesh& mesh = objects[obj];
view = glm::lookAt(testParams.m_EyePos, testParams.m_LookAtPos, glm::vec3(0, 1, 0));
//model = glm::rotate(model, glm::radians(0.5f), glm::vec3(0, 1, 0));
cb.m_ModelViewProj = proj * view * model;
// Kick off draw. Note that it blocks callee until drawcall is completed
pRenderContext->DrawIndexed(mesh.m_IdxCount, mesh.m_IdxOffset);
}
pRenderContext->EndRenderPass();На стороне приложения не происходит никакой магии: после подготовки контекста рендеринга стандартной конфигурацией, обычной привязки буфера кадров, буферов вершин/индексов, шейдеров и всего остального объекты рендерятся под одному мешу за раз. При этом свою задачу выполняет тайловый растеризатор; мы рассмотрим строку 18, в которой срабатывает вызов отрисовки. Обратите внимание на комментарий о том, что растеризатор блокирует поток вызвавшей функции, пока не будет обработан и завершён текущий вызов отрисовки. Очевидно, это сильно отличается от того, как работают реальные API и аппаратные растеризаторы: они никогда не обрабатывают только один вызов отрисовки за раз и не выполняют блокировку до его завершения; это было бы ужасно неэффективно. Вместо этого они обрабатывают «пакеты» (batches) команд, которые приложения записывают в буфер команд и при помощи графических драйверов передают оборудованию. Основные причины этого: 1) минимизация избыточного планирования работ CPU <-> GPU и 2) увеличение использования ресурсов GPU.
Теперь, когда мы примерно поняли, как сэмпл выполняет вызов отрисовки, можно переходить к тому, что происходит в растеризаторе. Если вы взглянете на каталог исходников проекта, то на этот раз увидите намного больше файлов. Однако самое важное обычно находится в Pipeline Thread и в Render Engine, а всё остальное обеспечивает вспомогательную функциональность. Render Engine обрабатывает подготовку вызовов отрисовки и различных ресурсов, необходимых для тайлового растеризатора, например групп для каждого тайла и буферов масок покрытия, а также обеспечивает синхронизацию между Pipeline Threads, каждый из которых порождает собственный поток для параллельного выполнения вышеупомянутых этапов конвейера. Как же Render Engine подготавливает вызов отрисовки для выполнения потоками конвейера?
// Prepare for next drawcall
ApplyPreDrawcallStateInvalidations();
uint32_t numRemainingPrims = primCount;
uint32_t drawElemsPrev = 0u;
uint32_t numIter = 0;
while (numRemainingPrims > 0)
{
// Prepare for next draw iteration
ApplyPreDrawIterationStateInvalidations();
// How many prims are to be processed this iteration & prims per thread
uint32_t iterationSize = (numRemainingPrims >= m_RenderConfig.m_MaxDrawIterationSize) ? m_RenderConfig.m_MaxDrawIterationSize : numRemainingPrims;
uint32_t perIterationRemainder = iterationSize % m_RenderConfig.m_NumPipelineThreads;
uint32_t primsPerThread = iterationSize / m_RenderConfig.m_NumPipelineThreads;
for (uint32_t threadIdx = 0; threadIdx < m_RenderConfig.m_NumPipelineThreads; threadIdx++)
{
uint32_t currentDrawElemsStart = drawElemsPrev;
uint32_t currentDrawElemsEnd = (threadIdx == (m_RenderConfig.m_NumPipelineThreads - 1)) ?
// If number of remaining primitives in iteration is not multiple of number of threads, have the last thread cover the remaining range
(currentDrawElemsStart + primsPerThread + perIterationRemainder) :
currentDrawElemsStart + primsPerThread;
// Threads must have been initialized and idle by now!
PipelineThread* pThread = m_PipelineThreads[threadIdx];
// Assign computed draw elems range for thread
pThread->m_ActiveDrawParams.m_ElemsStart = currentDrawElemsStart;
pThread->m_ActiveDrawParams.m_ElemsEnd = currentDrawElemsEnd;
pThread->m_ActiveDrawParams.m_VertexOffset = vertexOffset;
pThread->m_ActiveDrawParams.m_IsIndexed = isIndexed;
// PipelineThread drawcall input prepared, it can start processing of drawcall
pThread->m_CurrentState.store(ThreadStatus::DRAWCALL_TOP, std::memory_order_release);
drawElemsPrev = currentDrawElemsEnd;
numRemainingPrims -= (currentDrawElemsEnd - currentDrawElemsStart);
}
// All threads are assigned draw parameters, let them work now
m_DrawcallSetupComplete.store(true, std::memory_order_release);
// Stall main thread until all active threads complete given draw iteration
WaitForPipelineThreadsToCompleteProcessingDrawcall();
}Здесь мы равномерно разделяем входящие примитивы по потокам конвейера, чтобы масштабировать растеризатор при увеличении доступных потоков. Возможно, вы спросите, а что насчёт итераций? Они возникают потому, что мы никак не можем заранее узнать, будет ли следующий вызов отрисовки содержать 6 треугольников или 5 миллионов треугольников, и мы совершенно не хотим динамически выделять внутренние буферы или изменять их размер; так растеризатор перестал бы работать в реальном времени! Вместо этого мы задаём верхнюю границу (она может быть произвольно большой, мы подумаем, каким должен быть подходящий размер итераций) для наших внутренних буферов, выделим их один раз, а во время отрисовки будем просто выполнять итерации по наборам примитивов, разделённых на итерации, что логически аналогично выполнению этого всего за одну итерацию. Это похоже на то, как с этой неизвестностью справляются аппаратные растеризаторы.
Пример подготовки вызова отрисовки: 3 потока, параллельно обрабатывающих по 6 примитивов на итерацию
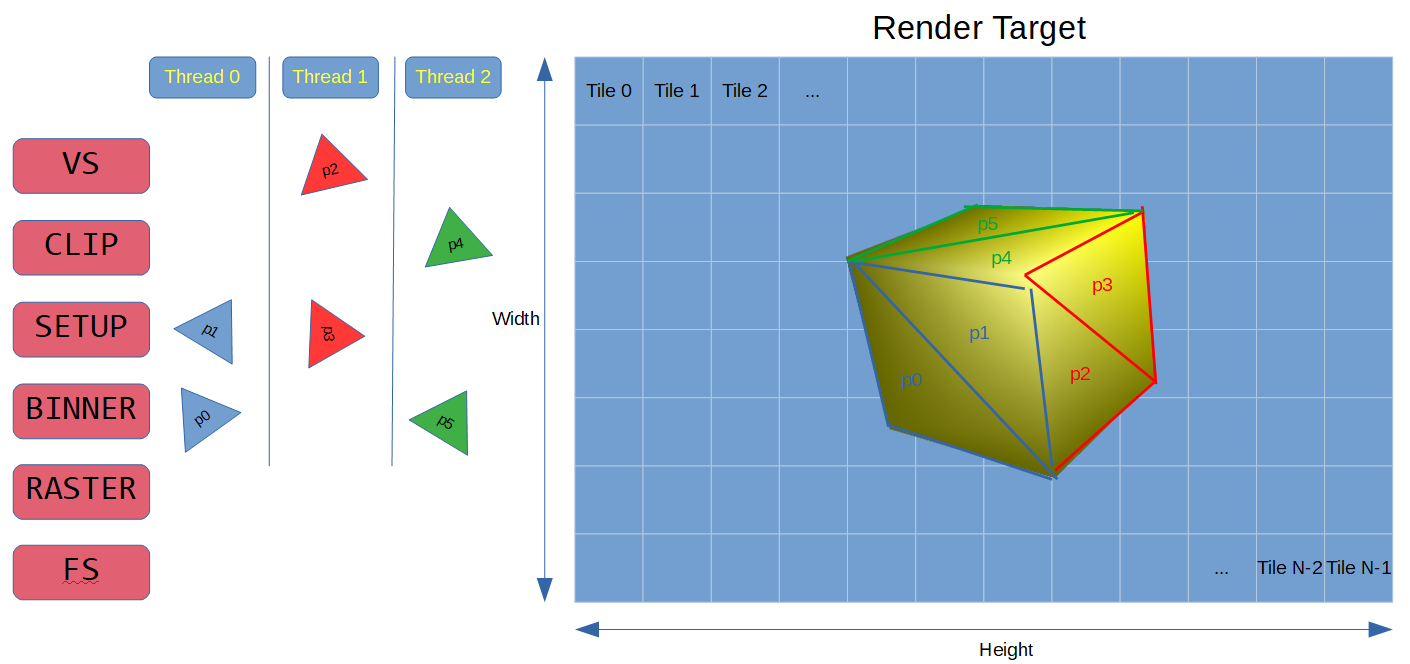
Могут возникать различные граничные случаи, например, когда количество примитивов не кратно количеству потоков или даже меньше количества потоков, поэтому мы здесь мы обрабатываем и их. Наличие верхней границы для внутренних буферов оправдывает себя, однако требует от нас дополнительного контроля, например, нужно делать недействительными устаревшие данные во внутренних структурах данных и кэшах перед каждой итерацией. Напоследок стоит заметить, что нужно, чтобы все потоки входили в соответствующие конвейеры не раньше того, пока есть хотя бы один поток, параметры вызовов отрисовки которого пока не назначены, чтобы это не вызывало проблем синхронизации; поэтому мы используем атомарный флаг m_DrawcallSetupComplete для приостановки потоков до завершения подготовки вызовов отрисовки. После этого потокам даётся зелёный свет и мы ждём, пока все итерации текущего вызова отрисовки обрабатываются потоками, чтобы вернуть исполнение в поток вызвавшей функции.
Теперь, когда мы увидели, как потоки включаются для обработки вызова отрисовки, можно внимательнее посмотреть на сам конвейер.
Обработка геометрии
Обработкой геометрии называется обработка вершин, получаемых из пользовательских буферов. Она состоит из этапов затенения вершин, усечения, подготовки треугольников и создания групп. Помните, что к этому моменту все потоки будут выполняться параллельно!
Обработка геометрии. при которой каждый поток итеративно обходит примитивы в заданном ему интервале
for (uint32_t drawIdx = m_ActiveDrawParams.m_ElemsStart, primIdx = m_ActiveDrawParams.m_ElemsStart % m_RenderConfig.m_MaxDrawIterationSize;
drawIdx < m_ActiveDrawParams.m_ElemsEnd;
drawIdx++, primIdx++)
{
// drawIdx = Assigned prim indices which will be only used to fetch indices
// primIdx = Prim index relative to current iteration
// Clip-space vertices to be retrieved from VS
glm::vec4 v0Clip, v1Clip, v2Clip;
// VS
ExecuteVertexShader<IsIndexed>(drawIdx, primIdx, &v0Clip, &v1Clip, &v2Clip);
// Bbox of the primitive which will be computed during clipping
Rect2D bbox;
// CLIPPER
if (!ExecuteFullTriangleClipping(primIdx, v0Clip, v1Clip, v2Clip, &bbox))
{
// Triangle clipped, proceed iteration with next primitive
continue;
}
// TRIANGLE SETUP & CULL
if (!ExecuteTriangleSetupAndCull(primIdx, v0Clip, v1Clip, v2Clip))
{
// Triangle culled, proceed iteration with next primitive
continue;
}
// BINNER
ExecuteBinner(primIdx, v0Clip, v1Clip, v2Clip, bbox);
}Конвейер, как и раньше, начинает с вершинного шейдера (VS), задача которого заключается в получении вершин/индексов из назначенных буферов вершин/индексов и в вызове заданной пользователем процедуры VS, возвращающей позиции в пространстве усечения, а также передающей атрибуты затенённым вершинам. Кроме того, он использует небольшой кэш вершинного шейдера, индивидуальный для каждого потока. Если вершина индексированного меша будет присутствовать в VS$, то вместо повторного вызова VS, кэшированная позиция пространства усечения и атрибуты вершин копируются непосредственно из кэша, что может сэкономить значительный объём вычислений при большом количестве вершин. В противном случае мы вызываем VS обычным образом и помещаем копию возвращённых данных вершин в VS$. После получения позиции в пространстве усечения и атрибутов мы также вызываем CalculateInterpolationCoefficients(), который вычисляет и сохраняет данные интерполяции, которые нам понадобятся для интерполяции атрибутов вершин перед их передачей в процедуру FS. Заметьте, что мы сохраняем в цикле копию преобразованных вершин, для эффективности критически важно, чтобы они хранились в L1/L2/L3 (перечисление от наилучшего до наихудшего случая), пока поток обрабатывает этапы геометрии.
После завершения VS и получения атрибутов вершин мы продолжаем усечением треугольником по пирамиде видимости и вычислением ограничивающих параллелограммов примитивов, т.е. ограничивающей площади экранного пространства. Как видно из названия функции, мы усекаем примитивы по дробности полных треугольников. Замечательно, но что это означает?
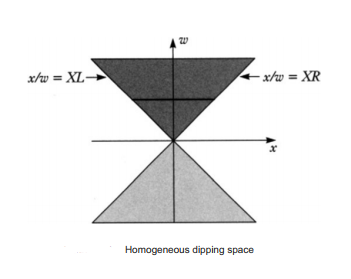
На показанном выше рисунке плоскости X-W (взятого из статьи Блинна Calculating Screen Coverage) тёмно-серая область в верхней части обозначает точки перед глазом, то есть полностью видимые, а нижняя область представляет точки за глазом. В функции усечения мы проверяем, находятся ли все три вершины треугольника полностью внутри видимой области, или в области Trivial-Accept (TA) или же полностью снаружи, или в области Trivial-Reject (TR). Если в TA, то мы можем безопасно вычислить ограничивающий параллелограмм примитива, применив однородное деление (например, деление на W), а если в TR, то мы можем без проблем отбросить весь примитив. В противном случае примитив должен иметь вершины в разных частях пирамиды видимости, то есть его нужно усекать плоскостями и отрисовывать частично. Однако особенностью алгоритма однородной растеризации является то, что его метод преобразования сканов может рендерить даже частично видимые примитивы, что подробнее рассматривалось в предыдущих постах и оригинальной статье. Следовательно, если возникает состояние «необходимо усечение» (т.е. треугольник не в TR и не в TA), то мы зададим ограничивающий параллелограмм (чрезвычайно консервативно!) как границы всего экрана.
После завершения усечения по полным треугольникам мы продолжаем этапом подготовки отсечения треугольников (Triangle Setup and Culling), на котором вычисляются знакомые коэффициенты уравнений рёбер. В отличие от реализации «Растеризации за одну неделю», на этот раз я реализовал оптимизации исходной статьи, которые позволяют умным образом избавиться от необходимости инвертирования матрицы вершин:
// First, transform clip-space (x, y, z, w) vertices to device-space 2D homogeneous coordinates (x, y, w)
const glm::vec4 v0Homogen = TO_HOMOGEN(v0Clip, fbWidth, fbHeight);
const glm::vec4 v1Homogen = TO_HOMOGEN(v1Clip, fbWidth, fbHeight);
const glm::vec4 v2Homogen = TO_HOMOGEN(v2Clip, fbWidth, fbHeight);
// To calculate EE coefficients, we need to set up a "vertex matrix" and invert it
// M = | x0 x1 x2 |
// | y0 y1 y2 |
// | w0 w1 w2 |
// Alternatively, we can rely on the following relation between an inverse and adjoint of a matrix: inv(M) = adj(M)/det(M)
// Since we use homogeneous coordinates, it's sufficient to only compute adjoint matrix:
// A = | a0 b0 c0 |
// | a1 b1 c1 |
// | a2 b2 c2 |
float a0 = (v2Homogen.y * v1Homogen.w) - (v1Homogen.y * v2Homogen.w);
float a1 = (v0Homogen.y * v2Homogen.w) - (v2Homogen.y * v0Homogen.w);
float a2 = (v1Homogen.y * v0Homogen.w) - (v0Homogen.y * v1Homogen.w);
float b0 = (v1Homogen.x * v2Homogen.w) - (v2Homogen.x * v1Homogen.w);
float b1 = (v2Homogen.x * v0Homogen.w) - (v0Homogen.x * v2Homogen.w);
float b2 = (v0Homogen.x * v1Homogen.w) - (v1Homogen.x * v0Homogen.w);
float c0 = (v2Homogen.x * v1Homogen.y) - (v1Homogen.x * v2Homogen.y);
float c1 = (v0Homogen.x * v2Homogen.y) - (v2Homogen.x * v0Homogen.y);
float c2 = (v1Homogen.x * v0Homogen.y) - (v0Homogen.x * v1Homogen.y);
// Additionally,
// det(M) == 0 -> degenerate/zero-area triangle
// det(M) < 0 -> back-facing triangle
float detM = (c0 * v0Homogen.w) + (c1 * v1Homogen.w) + (c2 * v2Homogen.w);
// Assign computed EE coefficients for given primitive
m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * primIdx + 0] = { a0, b0, c0 };
m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * primIdx + 1] = { a1, b1, c1 };
m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * primIdx + 2] = { a2, b2, c2 };Ещё одно преимущество этой техники заключается в том, что она позволяет нам использовать одинаковые коэффициенты уравнений рёбер и для преобразования сканов, и для интерполяции атрибутов. В прошлый раз мы вычисляли вектор интерполяции параметров для каждого отдельного параметра, что может быстро стать узким местом, если у нас будет больше атрибутов, а не просто несколько скалярных значений, например, нормалей + координат текстур. После завершения подготовки треугольников (Triangle Setup) мы перешли к очень важной части тайлового растеризатора, а именно к группированию (Binning) (многие понятия которого превосходно были объяснены не кем иным, как самим Майклом Абрашем). Роль Binning-а в конвейере огромна: он должен находить, какие тайлы покрывают какие примитивы, или, иными словами, какие примитивы накладываются на какие тайлы. Стоит учесть, что тайл — это подобласть render target, по умолчанию состоящая из 8×8 блоков.
Для этого мы просто смотрим на отдельный треугольник и на то, как он будет обрабатываться, но помните, что всё это выполняется параллельно несколькими потоками. И реализовать это легко: для каждого тайла мы выделяем массив пересекающихся примитивов на каждый поток. То есть поместив примитивы группы каждого потока в собственную группу каждого потока, мы можем заставить их работать одновременно и без необходимости синхронизации. Кроме того, таким образом мы сохраним порядок рендеринга примитивов, позже пройдя по сгруппированным примитивам в порядке потоков.
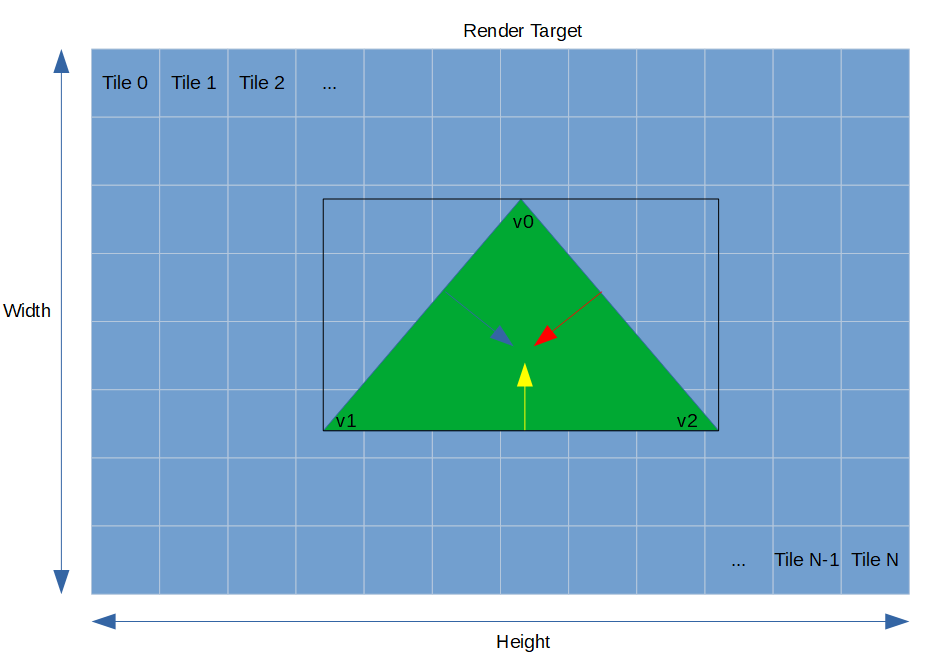
Цветными стрелками обозначены нормали рёбер, а прямоугольником — ограничивающий параллелограмм треугольника.
Исходя из примитива, его ограничивающего параллелограмма и коэффициентов уравнений рёбер, группа предоставляет нам следующую информацию:
- Trivial-Accept: тайл, находящийся внутри ограничивающего параллелограмма треугольника полностью покрыт треугольником
- Trivial-Reject: тайл, находящийся внутри ограничивающего параллелограмма треугольника, полностью находится вне треугольника
- Overlap: тайл, находящийся внутри ограничивающего параллелограмма треугольника, пересекается с треугольником
Чем же это нам полезно? Допустим, мы выбрали размер тайла 64×64 пикселя; тогда тривиальное отбрасывание (Trivial-Reject) тайла означает, что мы можем разом пропустить 64×64 попиксельных теста. Аналогично, тривиальное принятие (Trivial-Accept) тайла означает, что 64×64 пикселя видимы и нужно просто отрисовать весь тайл! Overlap — наименее предпочтительный здесь результат, потому что он означает, что тайл и примитив требуют дальнейшей обработки на этапе растеризации, где мы спускаемся на уровень блоков и применяем проверку рёбер на более мелком уровне.
Процесс группирования (binning) мы начинаем с того, что сначала находим минимальный и максимальный индексы тайлов, покрываемых ограничивающим параллелограммом треугольника:
// Given a tile size and frame buffer dimensions, find min/max range of the tiles that fall within bbox computed above
// which we're going to iterate over, in order to determine if the primitive should be binned or not
// Use floor(), min indices are inclusive
uint32_t minTileX = static_cast<uint32_t>(glm::floor(bbox.m_MinX / m_RenderConfig.m_TileSize));
uint32_t minTileY = static_cast<uint32_t>(glm::floor(bbox.m_MinY / m_RenderConfig.m_TileSize));
// Use ceil(), max indices are exclusive
uint32_t maxTileX = static_cast<uint32_t>(glm::ceil(bbox.m_MaxX / m_RenderConfig.m_TileSize));
uint32_t maxTileY = static_cast<uint32_t>(glm::ceil(bbox.m_MaxY / m_RenderConfig.m_TileSize));После получения коэффициентов уравнений рёбер мы задаём углы TR и TA каждого ребра:
// Fetch edge equation coefficients computed in triangle setup
glm::vec3 ee0 = m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * primIdx + 0];
glm::vec3 ee1 = m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * primIdx + 1];
glm::vec3 ee2 = m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * primIdx + 2];
// Normalize edge functions
ee0 /= (glm::abs(ee0.x) + glm::abs(ee0.y));
ee1 /= (glm::abs(ee1.x) + glm::abs(ee1.y));
ee2 /= (glm::abs(ee2.x) + glm::abs(ee2.y));
// Indices of tile corners:
// LL -> 0 LR -> 1
// UL -> 2 UR -> 3
static const glm::vec2 scTileCornerOffsets[] =
{
{ 0.f, 0.f}, // LL
{ m_RenderConfig.m_TileSize, 0.f }, // LR
{ 0.f, m_RenderConfig.m_TileSize }, // UL
{ m_RenderConfig.m_TileSize, m_RenderConfig.m_TileSize} // UR
};
// (x, y) -> sample location | (a, b, c) -> edge equation coefficients
// E(x, y) = (a * x) + (b * y) + c
// E(x + s, y + t) = E(x, y) + (a * s) + (b * t)
// Based on edge normal n=(a, b), set up tile TR corners for each edge
const uint8_t edge0TRCorner = (ee0.y >= 0.f) ? ((ee0.x >= 0.f) ? 3u : 2u) : (ee0.x >= 0.f) ? 1u : 0u;
const uint8_t edge1TRCorner = (ee1.y >= 0.f) ? ((ee1.x >= 0.f) ? 3u : 2u) : (ee1.x >= 0.f) ? 1u : 0u;
const uint8_t edge2TRCorner = (ee2.y >= 0.f) ? ((ee2.x >= 0.f) ? 3u : 2u) : (ee2.x >= 0.f) ? 1u : 0u;
// TA corner is the one diagonal from TR corner calculated above
const uint8_t edge0TACorner = 3u - edge0TRCorner;
const uint8_t edge1TACorner = 3u - edge1TRCorner;
const uint8_t edge2TACorner = 3u - edge2TRCorner;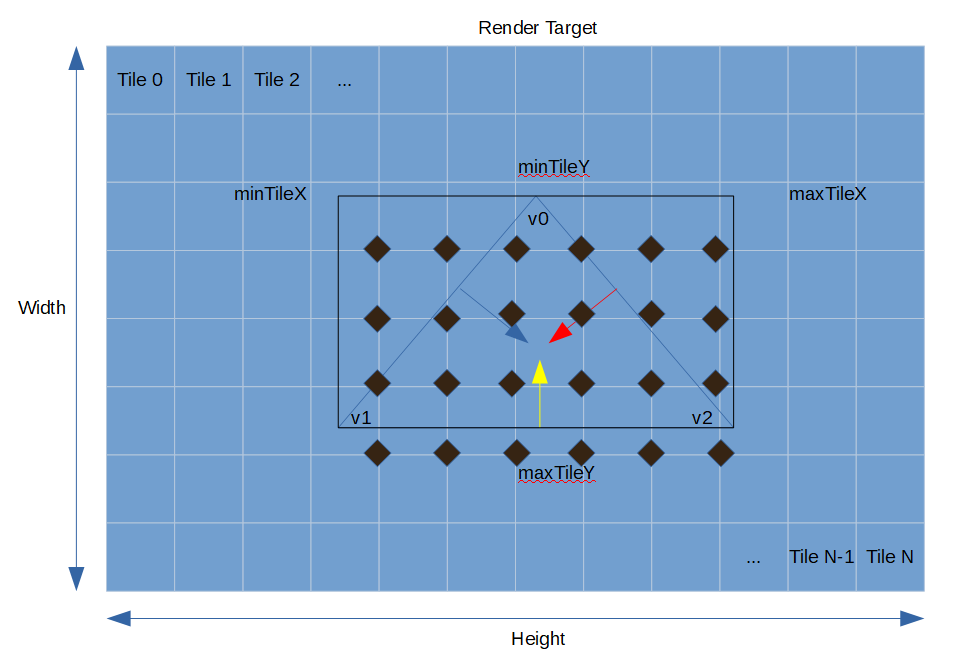
Отмечен угол TR для каждого тайла ребра 2 (ось X направлена вправо, ось Y — вниз!)
Угол TR тайла — это угол, находящийся наиболее глубоко в ребре, а угол TA — наиболее снаружи. Углы TR и TA нужны нам потому, что если мы придём к выводу, что угол TR любого ребра находится за пределами ребра, то весь тайл должен быть за пределами треугольника, а значит, его можно тривиально отбросить. Аналогично, если углы TA всех рёбер находятся внутри соответствующих рёбер, то весь тайл должен находиться внутри треугольника (или наоборот), а следовательно, его можно тривиально принять.
Способ поиска этих углов в приведённом выше фрагменте кода — одна из самых важных частей тайловго растеризатора: мы выбираем углы TR/TA на основании наклона нормали ребра =(a, b) (a, b — это компоненты x и y нормали). На показанном выше рисунке мы можем видеть, что для ребра 2 (т.е. для синей стрелки) угол TR для всех тайлов помечен как правый нижний. Почему? Для ребра 2 справедливо (a > 0), то есть ребро должно удлиняться влево, то есть один из правых углов (нижний или верхний) должен быть ближе к ребру, чем левый. Аналогично, (b > 0), то есть угол TR должен быть правым нижним углом. У нас есть два варианта нахождения угла TA: или применить ту же логику, или положиться на тот факт, что самый дальний угол от угла TR будет находиться наиболее снаружи, что находится на диагонали от угла TR, что более оптимально.
// Iterate over calculated range of tiles
for (uint32_t ty = minTileY, tyy = 0; ty < maxTileY; ty++, tyy++)
{
for (uint32_t tx = minTileX, txx = 0; tx < maxTileX; tx++, txx++)
{
// Using EE coefficients calculated in TriangleSetup stage and positive half-space tests, determine one of three cases possible for each tile:
// 1) TrivialReject -- tile within tri's bbox does not intersect tri -> move on
// 2) TrivialAccept -- tile within tri's bbox is completely within tri -> emit a full-tile coverage mask
// 3) Overlap -- tile within tri's bbox intersects tri -> bin the triangle to given tile for further rasterization where block/pixel-level coverage masks will be emitted
// (txx, tyy) = how many steps are done per dimension
const float txxOffset = static_cast<float>(txx * m_RenderConfig.m_TileSize);
const float tyyOffset = static_cast<float>(tyy * m_RenderConfig.m_TileSize);
// Step from edge function computed above for the first tile in bbox
float edgeFuncTR0 = edgeFunc0 + ((ee0.x * (scTileCornerOffsets[edge0TRCorner].x + txxOffset)) + (ee0.y * (scTileCornerOffsets[edge0TRCorner].y + tyyOffset)));
float edgeFuncTR1 = edgeFunc1 + ((ee1.x * (scTileCornerOffsets[edge1TRCorner].x + txxOffset)) + (ee1.y * (scTileCornerOffsets[edge1TRCorner].y + tyyOffset)));
float edgeFuncTR2 = edgeFunc2 + ((ee2.x * (scTileCornerOffsets[edge2TRCorner].x + txxOffset)) + (ee2.y * (scTileCornerOffsets[edge2TRCorner].y + tyyOffset)));
// If TR corner of the tile is outside any edge, reject whole tile
bool TRForEdge0 = (edgeFuncTR0 < 0.f);
bool TRForEdge1 = (edgeFuncTR1 < 0.f);
bool TRForEdge2 = (edgeFuncTR2 < 0.f);
if (TRForEdge0 || TRForEdge1 || TRForEdge2)
{
LOG("Tile %d TR'd by thread %dn", m_pRenderEngine->GetGlobalTileIndex(tx, ty), m_ThreadIdx);
// TrivialReject
// Tile is completely outside of one or more edges
continue;
}
else
{
// Tile is partially or completely inside one or more edges, do TrivialAccept tests first
// Compute edge functions at TA corners based on edge function at first tile origin
float edgeFuncTA0 = edgeFunc0 + ((ee0.x * (scTileCornerOffsets[edge0TACorner].x + txxOffset)) + (ee0.y * (scTileCornerOffsets[edge0TACorner].y + tyyOffset)));
float edgeFuncTA1 = edgeFunc1 + ((ee1.x * (scTileCornerOffsets[edge1TACorner].x + txxOffset)) + (ee1.y * (scTileCornerOffsets[edge1TACorner].y + tyyOffset)));
float edgeFuncTA2 = edgeFunc2 + ((ee2.x * (scTileCornerOffsets[edge2TACorner].x + txxOffset)) + (ee2.y * (scTileCornerOffsets[edge2TACorner].y + tyyOffset)));
// If TA corner of the tile is outside all edges, accept whole tile
bool TAForEdge0 = (edgeFuncTA0 >= 0.f);
bool TAForEdge1 = (edgeFuncTA1 >= 0.f);
bool TAForEdge2 = (edgeFuncTA2 >= 0.f);
if (TAForEdge0 && TAForEdge1 && TAForEdge2)
{
// TrivialAccept
// Tile is completely inside of the triangle, no further rasterization is needed,
// whole tile will be fragment-shaded!
LOG("Tile %d TA'd by thread %dn", m_pRenderEngine->GetGlobalTileIndex(tx, ty), m_ThreadIdx);
// Append tile to the rasterizer queue
m_pRenderEngine->EnqueueTileForRasterization(m_pRenderEngine->GetGlobalTileIndex(tx, ty));
CoverageMask mask;
mask.m_SampleX = static_cast<uint32_t>(tilePosX + txxOffset); // Based off of first tile position calculated above
mask.m_SampleY = static_cast<uint32_t>(tilePosY + tyyOffset); // Based off of first tile position calculated above
mask.m_PrimIdx = primIdx;
mask.m_Type = CoverageMaskType::TILE;
// Emit full-tile coverage mask
m_pRenderEngine->AppendCoverageMask(
m_ThreadIdx,
m_pRenderEngine->GetGlobalTileIndex(tx, ty),
mask);
}
else
{
LOG("Tile %d binned by thread %dn", m_pRenderEngine->GetGlobalTileIndex(tx, ty), m_ThreadIdx);
// Overlap
// Tile is partially covered by the triangle, bin the triangle for the tile
m_pRenderEngine->BinPrimitiveForTile(
m_ThreadIdx,
m_pRenderEngine->GetGlobalTileIndex(tx, ty),
primIdx);
}
}
}
}Найдя углы TR и TA всех трёх рёбер, мы переходим в цикл, где итеративно обходим тайлы в интервале [minTile{X|Y}, maxTile{X|Y}), чтобы применить к каждому тайлу проверку на наличие внутри/снаружи. Это тот же тест, который мы видели ранее; единственное отличие заключается в том, что тест выполняется для углов TR/TA тайлов. Если тайл отброшен по TR, мы двигаемся дальше. Если тайл одобрен по TA, то мы создаём маску покрытия для всего тайла (и помещаем тайл в очередь растеризатора), после чего продолжаем. В неудачном случае, когда тайл пересекается с примитивом, мы добавляем примитив в группу потока тайла, что делается так:
void RenderEngine::BinPrimitiveForTile(uint32_t threadIdx, uint32_t tileIdx, uint32_t primIdx)
{
// Add primIdx to the per-thread bin of a tile
std::vector<uint32_t>& tileBin = m_BinList[tileIdx][threadIdx];
if (tileBin.empty())
{
// First encounter of primitive for tile, enqueue it for rasterization
EnqueueTileForRasterization(tileIdx);
}
else
{
// Tile must have been already appended to the work queue
ASSERT(m_TileList[tileIdx].m_IsTileQueued.test_and_set());
}
// Append primIdx to the tile's bin
tileBin.push_back(primIdx);
}void RenderEngine::EnqueueTileForRasterization(uint32_t tileIdx)
{
// Append the tile to the rasterizer queue if not already done
if (!m_TileList[tileIdx].m_IsTileQueued.test_and_set(std::memory_order_acq_rel))
{
// Tile not queued up for rasterization, do so now
m_RasterizerQueue.InsertTileIndex(tileIdx);
}
}Очередь растеризатора — это простой FIFO индексов тайлов, ожидающих растеризации (в случае, если тайл пересекается с примитивом) или затеняемых пофрагментно (тайлы, одобренные по TA) на следующих этапах. На этом можно завершить обработку геометрии и перейти к растеризации. Для сравнения вот пример Hello, Triangle! по умолчанию и тривиально принимаемые тайлы:


Растеризация
Прежде чем любой из потоков сможет перейти к этапу растеризации, они простаивают, пока все потоки не достигнут этапа постгруппировки (post-binning), который необходим для определения того, что все примитивы были сгруппированы в тайлы перед началом работы растеризатора. Как только все потоки завершат все этапы обработки геометрии, они начинаю обрабатывать тайлы из очереди растеризатора.
// To preserve rendering order, we must ensure that all threads finish binning primitives to tiles
// before rasterization is started. To do that, we will stall all threads to sync @DRAWCALL_RASTERIZATION
// Set state to post binning and stall until all PipelineThreads complete binning
m_CurrentState.store(ThreadStatus::DRAWCALL_SYNC_POINT_POST_BINNER, std::memory_order_release);
m_pRenderEngine->WaitForPipelineThreadsToCompleteBinning();Если вы поняли идею группирования, то суть растеризатора очень проста: мы применяем тот же набор проверок TR/TA, на этот раз на уровне блоков, спускаясь с уровня тайлов:
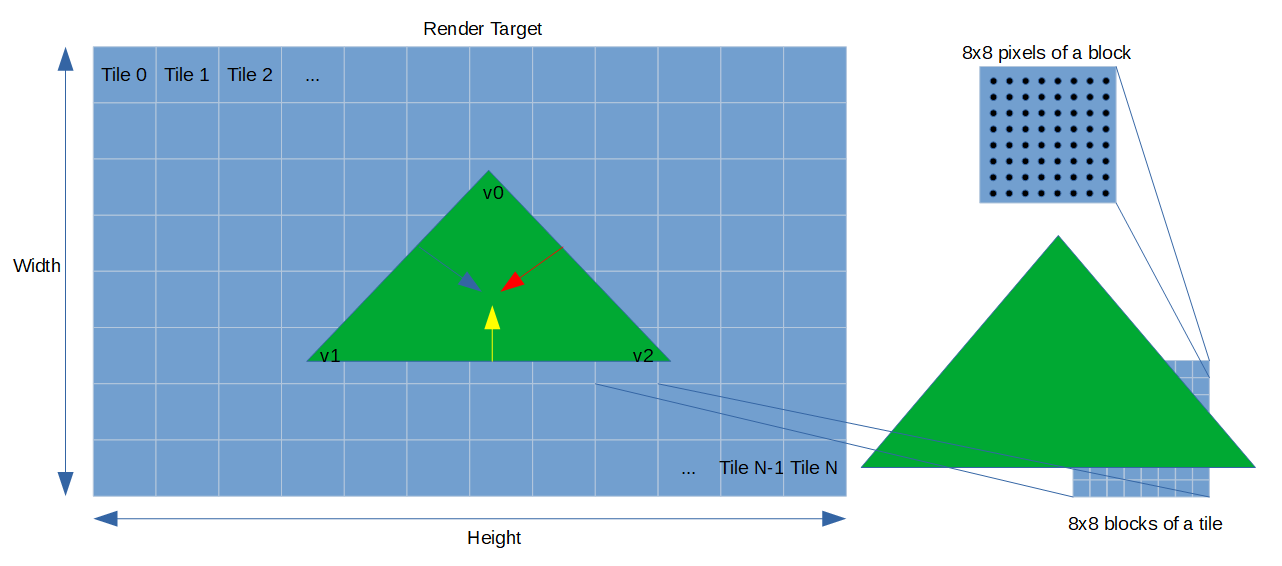
Потоки получают следующий доступный индекс тайла из очереди растеризатора и обрабатывают этот тайл, снова параллельно применяя вышеописанные проверки ко всем примитивам, сгруппированным и привязанным к этому тайлу.
Как и на этапе группировки, при помощи ограничивающего параллелограмма мы находим максимальный и минимальный индексы блоков, которые пересекаются с примитивов, определяем углы TR/TA блоков для всех рёбер и обходим в цикле весь интервал, проверяя, можно ли подвергнуть блоки TR или TA, или полностью проигнорировать. Если блок снова отбрасывается TR, мы продолжаем двигаться дальше. Если он удовлетворяет TA, то мы создаём маску покрытия для всего блока и продолжаем. В противном случае нам нужно опуститься ещё ниже, на уровень пикселей, чтобы выполнять проверку рёбер и создавать маски покрытия для пикселей. Удобно то, что благодаря SIMD мы можем растеризировать несколько пикселей параллельно:
// Position of the block that we're testing at pixel level
float blockPosX = (firstBlockWithinBBoxX + bxxOffset);
float blockPosY = (firstBlockWithinBBoxY + byyOffset);
// Compute E(x, y) = (x * a) + (y * b) c at block origin once
__m128 sseEdge0FuncAtBlockOrigin = _mm_set1_ps(ee0.z + ((ee0.x * blockPosX) + (ee0.y * blockPosY)));
__m128 sseEdge1FuncAtBlockOrigin = _mm_set1_ps(ee1.z + ((ee1.x * blockPosX) + (ee1.y * blockPosY)));
__m128 sseEdge2FuncAtBlockOrigin = _mm_set1_ps(ee2.z + ((ee2.x * blockPosX) + (ee2.y * blockPosY)));
// Store edge 0 equation coefficients
__m128 sseEdge0A4 = _mm_set_ps1(ee0.x);
__m128 sseEdge0B4 = _mm_set_ps1(ee0.y);
// Store edge 1 equation coefficients
__m128 sseEdge1A4 = _mm_set_ps1(ee1.x);
__m128 sseEdge1B4 = _mm_set_ps1(ee1.y);
// Store edge 2 equation coefficients
__m128 sseEdge2A4 = _mm_set_ps1(ee2.x);
__m128 sseEdge2B4 = _mm_set_ps1(ee2.y);
// Generate masks used for tie-breaking rules (not to double-shade along shared edges)
__m128 sseEdge0A4PositiveOrB4NonNegativeA4Zero = _mm_or_ps(_mm_cmpgt_ps(sseEdge0A4, _mm_setzero_ps()),
_mm_and_ps(_mm_cmpge_ps(sseEdge0B4, _mm_setzero_ps()), _mm_cmpeq_ps(sseEdge0A4, _mm_setzero_ps())));
__m128 sseEdge1A4PositiveOrB4NonNegativeA4Zero = _mm_or_ps(_mm_cmpgt_ps(sseEdge1A4, _mm_setzero_ps()),
_mm_and_ps(_mm_cmpge_ps(sseEdge1B4, _mm_setzero_ps()), _mm_cmpeq_ps(sseEdge1A4, _mm_setzero_ps())));
__m128 sseEdge2A4PositiveOrB4NonNegativeA4Zero = _mm_or_ps(_mm_cmpgt_ps(sseEdge2A4, _mm_setzero_ps()),
_mm_and_ps(_mm_cmpge_ps(sseEdge2B4, _mm_setzero_ps()), _mm_cmpeq_ps(sseEdge2A4, _mm_setzero_ps())));
for (uint32_t py = 0; py < g_scPixelBlockSize; py++)
{
// Store Y positions in current row (all samples on the same row has the same Y position)
__m128 sseY4 = _mm_set_ps1(py + 0.5f);
for (uint32_t px = 0; px < g_scNumEdgeTestsPerRow; px++)
{
// E(x, y) = (x * a) + (y * b) + c
// E(x + s, y + t) = E(x, y) + s * a + t * b
// Store X positions of 4 consecutive samples
__m128 sseX4 = _mm_setr_ps(
g_scSIMDWidth * px + 0.5f,
g_scSIMDWidth * px + 1.5f,
g_scSIMDWidth * px + 2.5f,
g_scSIMDWidth * px + 3.5f);
// a * s
__m128 sseEdge0TermA = _mm_mul_ps(sseEdge0A4, sseX4);
__m128 sseEdge1TermA = _mm_mul_ps(sseEdge1A4, sseX4);
__m128 sseEdge2TermA = _mm_mul_ps(sseEdge2A4, sseX4);
// b * t
__m128 sseEdge0TermB = _mm_mul_ps(sseEdge0B4, sseY4);
__m128 sseEdge1TermB = _mm_mul_ps(sseEdge1B4, sseY4);
__m128 sseEdge2TermB = _mm_mul_ps(sseEdge2B4, sseY4);
// E(x+s, y+t) = E(x,y) + a*s + t*b
__m128 sseEdgeFunc0 = _mm_add_ps(sseEdge0FuncAtBlockOrigin, _mm_add_ps(sseEdge0TermA, sseEdge0TermB));
__m128 sseEdgeFunc1 = _mm_add_ps(sseEdge1FuncAtBlockOrigin, _mm_add_ps(sseEdge1TermA, sseEdge1TermB));
__m128 sseEdgeFunc2 = _mm_add_ps(sseEdge2FuncAtBlockOrigin, _mm_add_ps(sseEdge2TermA, sseEdge2TermB));
//E(x, y):
// E(x, y) > 0
// ||
// !E(x, y) < 0 && (a > 0 || (a = 0 && b >= 0))
//
// Edge 0 test
__m128 sseEdge0Positive = _mm_cmpgt_ps(sseEdgeFunc0, _mm_setzero_ps());
__m128 sseEdge0Negative = _mm_cmplt_ps(sseEdgeFunc0, _mm_setzero_ps());
__m128 sseEdge0FuncMask = _mm_or_ps(sseEdge0Positive,
_mm_andnot_ps(sseEdge0Negative, sseEdge0A4PositiveOrB4NonNegativeA4Zero));
// Edge 1 test
__m128 sseEdge1Positive = _mm_cmpgt_ps(sseEdgeFunc1, _mm_setzero_ps());
__m128 sseEdge1Negative = _mm_cmplt_ps(sseEdgeFunc1, _mm_setzero_ps());
__m128 sseEdge1FuncMask = _mm_or_ps(sseEdge1Positive,
_mm_andnot_ps(sseEdge1Negative, sseEdge1A4PositiveOrB4NonNegativeA4Zero));
// Edge 2 test
__m128 sseEdge2Positive = _mm_cmpgt_ps(sseEdgeFunc2, _mm_setzero_ps());
__m128 sseEdge2Negative = _mm_cmplt_ps(sseEdgeFunc2, _mm_setzero_ps());
__m128 sseEdge2FuncMask = _mm_or_ps(sseEdge2Positive,
_mm_andnot_ps(sseEdge2Negative, sseEdge2A4PositiveOrB4NonNegativeA4Zero));
// Combine resulting masks of all three edges
__m128 sseEdgeFuncResult = _mm_and_ps(sseEdge0FuncMask,
_mm_and_ps(sseEdge1FuncMask, sseEdge2FuncMask));
uint16_t maskInt = static_cast<uint16_t>(_mm_movemask_ps(sseEdgeFuncResult));
// If at least one sample is visible, emit coverage mask for the tile
if (maskInt != 0x0)
{
// Quad mask points to the first sample
CoverageMask mask;
mask.m_SampleX = static_cast<uint32_t>(blockPosX + (g_scSIMDWidth * px));
mask.m_SampleY = static_cast<uint32_t>(blockPosY + py);
mask.m_PrimIdx = primIdx;
mask.m_Type = CoverageMaskType::QUAD;
mask.m_QuadMask = maskInt;
// Emit a quad mask
m_pRenderEngine->AppendCoverageMask(m_ThreadIdx, nextTileIdx, mask);
}
}
}Если вы простите меня за этот уродливый SIMD-суп (частично я виню в нём MSVC, которая генерирует довольно неоптимальный для таких тривиальных арифметических операций код), то разобраться в нём будет достаточно просто: мы берём 4 пикселя в строке блока, по умолчанию имеющего размер 8×8, выполняем проверки рёбер и генерируем маску покрытия для группы из 4 фрагментов. Если найдена хотя бы одна такая группа, в которой видим хотя бы один сэмпл (например, проверка if (maskInt != 0x0), мы создаём маску покрытия для этой группы фрагментов и продолжаем, пока итеративно не обойдём все пиксели в блоке. Повторяем процесс для всех блоков в интервале. В этом и заключается смысл растеризатора!
Хитрость здесь заключается в том, что лишние затраты на растеризацию оправдывают себя только на очень мелком уровне, а большинство сгруппированных треугольников тайла больше, чем один блок, потому что в противном случае нам придётся отбросить все вычисления, сделанные на более высоких уровнях; именно поэтому в аппаратных реализациях обычно существуют различные оптимизации для мелких треугольников.
Затенение фрагментов
Достигнув этапа пострастеризации, мы сталкиваемся с ещё одной точкой синхронизации:
// Rasterization completed, set state to post raster and
// stall until all PipelineThreads complete rasterization.
// We need this sync because when (N-x) threads finish rasterization and
// reach the end of tile queue while x threads are still busy rasterizing tile blocks,
// we must ensure that none of the (N-x) non-busy threads will go ahead and start fragment-shading tiles
// whose blocks could be currently still rasterized by x remaining threads
m_CurrentState.store(ThreadStatus::DRAWCALL_SYNC_POINT_POST_RASTER, std::memory_order_release);
m_pRenderEngine->WaitForPipelineThreadsToCompleteRasterization();Сделав так, чтобы все потоки достигли этапа затенения фрагментов (FS) одновременно после простоя до завершения растеризации, мы переходим к последнему этапу конвейера. Как и этап растеризации, этап FS параллельно работает с тайлами, полученными из очереди растеризатора, используя маски покрытия, созданные нами сначала на этапе группирования (Binning), а затем на этапе растеризации.
auto& currentSlot = pCoverageMaskBuffer->m_AllocationList[numAlloc];
for (uint32_t numMask = 0; numMask < currentSlot.m_AllocationCount; numMask++)
{
ASSERT(pCoverageMaskBuffer->m_AllocationList[numAlloc].m_pData != nullptr);
CoverageMask* pMask = &currentSlot.m_pData[numMask];
// In many cases, next N coverage masks will have been generated for the same primitive
// that we're fragment-shading at tile, block or fragment levels here,
// it could be optimized so that the EE coefficients of the same primitive won't be fetched
// from memory over and over again, unsure what gain, if anything it'd yield...
// First fetch EE coefficients that will be used (in addition to edge in/out tests) for perspective-correct interpolation of vertex attributes
const glm::vec3 ee0 = m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * pMask->m_PrimIdx + 0];
const glm::vec3 ee1 = m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * pMask->m_PrimIdx + 1];
const glm::vec3 ee2 = m_pRenderEngine->m_SetupBuffers.m_pEdgeCoefficients[3 * pMask->m_PrimIdx + 2];
// Store edge 0 coefficients
__m128 sseA4Edge0 = _mm_set_ps1(ee0.x);
__m128 sseB4Edge0 = _mm_set_ps1(ee0.y);
__m128 sseC4Edge0 = _mm_set_ps1(ee0.z);
// Store edge 1 equation coefficients
__m128 sseA4Edge1 = _mm_set_ps1(ee1.x);
__m128 sseB4Edge1 = _mm_set_ps1(ee1.y);
__m128 sseC4Edge1 = _mm_set_ps1(ee1.z);
// Store edge 2 equation coefficients
__m128 sseA4Edge2 = _mm_set_ps1(ee2.x);
__m128 sseB4Edge2 = _mm_set_ps1(ee2.y);
__m128 sseC4Edge2 = _mm_set_ps1(ee2.z);
const SIMDEdgeCoefficients simdEERegs =
{
sseA4Edge0,
sseA4Edge1,
sseA4Edge2,
sseB4Edge0,
sseB4Edge1,
sseB4Edge2,
sseC4Edge0,
sseC4Edge1,
sseC4Edge2,
};
switch (pMask->m_Type)
{
case CoverageMaskType::TILE:
LOG("Thread %d fragment-shading tile %dn", m_ThreadIdx, nextTileIdx);
FragmentShadeTile(pMask->m_SampleX, pMask->m_SampleY, pMask->m_PrimIdx, simdEERegs);
break;
case CoverageMaskType::BLOCK:
LOG("Thread %d fragment-shading blocksn", m_ThreadIdx);
FragmentShadeBlock(pMask->m_SampleX, pMask->m_SampleY, pMask->m_PrimIdx, simdEERegs);
break;
case CoverageMaskType::QUAD:
LOG("Thread %d fragment-shading coverage masksn", m_ThreadIdx, ee0, ee1, ee2);
FragmentShadeQuad(pMask, simdEERegs);
break;
default:
ASSERT(false);
break;
}
}Прежде чем мы вызовем пользовательскую процедуру FS, нам сначала нужно вычислить то, что называется базисными функциями параметров, которые являются непосредственной реализацией метода, описанного в статье, ссылку на которую я давал выше. Суть в том, что вместо вычисления вектора интерполяции для каждого параметра, мы находим базисные функции, которыми можно интерполировать (корректно с точки зрения перспективы) любой параметр:

void PipelineThread::ComputeParameterBasisFunctions(
uint32_t sampleX,
uint32_t sampleY,
const SIMDEdgeCoefficients& simdEERegs,
__m128* pSSEf0XY,
__m128* pSSEf1XY)
{
// R(x, y) = F0(x, y) + F1(x, y) + F2(x, y)
// r = 1/(F0(x, y) + F1(x, y) + F2(x, y))
// Store X positions of 4 consecutive samples
__m128 sseX4 = _mm_setr_ps(
sampleX + 0.5f,
sampleX + 1.5f,
sampleX + 2.5f,
sampleX + 3.5f); // x x+1 x+2 x+3
// Store Y positions of 4 samples in a row (constant)
__m128 sseY4 = _mm_set_ps1(sampleY); // y y y y
// Compute F0(x,y)
__m128 sseF0XY4 = _mm_add_ps(simdEERegs.m_SSEC4Edge0,
_mm_add_ps(
_mm_mul_ps(sseY4, simdEERegs.m_SSEB4Edge0),
_mm_mul_ps(sseX4, simdEERegs.m_SSEA4Edge0)));
// Compute F1(x,y)
__m128 sseF1XY4 = _mm_add_ps(simdEERegs.m_SSEC4Edge1,
_mm_add_ps(
_mm_mul_ps(sseY4, simdEERegs.m_SSEB4Edge1),
_mm_mul_ps(sseX4, simdEERegs.m_SSEA4Edge1)));
// Compute F2(x,y)
__m128 sseF2XY4 = _mm_add_ps(simdEERegs.m_SSEC4Edge2,
_mm_add_ps(
_mm_mul_ps(sseY4, simdEERegs.m_SSEB4Edge2),
_mm_mul_ps(sseX4, simdEERegs.m_SSEA4Edge2)));
// Compute F(x,y) = F0(x,y) + F1(x,y) + F2(x,y)
__m128 sseR4 = _mm_add_ps(sseF2XY4, _mm_add_ps(sseF0XY4, sseF1XY4));
// Compute perspective correction factor
sseR4 = _mm_rcp_ps(sseR4);
// Assign final f0(x,y) & f1(x,y)
*pSSEf0XY = _mm_mul_ps(sseR4, sseF0XY4);
*pSSEf1XY = _mm_mul_ps(sseR4, sseF1XY4);
// Basis functions f0, f1, f2 sum to 1, e.g. f0(x,y) + f1(x,y) + f2(x,y) = 1 so we'll skip computing f2(x,y) explicitly
}Реализация для разных масок покрытия (тайлов/блоков/четырёхугольников) почти одинакова, поэтому для полноты обзора я использовал маски четырёхугольников. Заметьте, что это самый сжатый путь выполнения кода, поэтому мы стремимся как можно активнее использовать SIMD.
void PipelineThread::FragmentShadeQuad(CoverageMask* pMask, const SIMDEdgeCoefficients& simdEERegs)
{
FragmentShader FS = m_pRenderEngine->m_FragmentShader;
// Vertex attributes to be interpolated and passed to FS
InterpolatedAttributes interpolatedAttribs;
// Parameter interpolation basis functions
__m128 ssef0XY, ssef1XY;
// Calculate basis functions f0(x,y) & f1(x,y) once
ComputeParameterBasisFunctions(
pMask->m_SampleX,
pMask->m_SampleY,
simdEERegs,
&ssef0XY,
&ssef1XY);
// Interpolate depth values prior to depth test
__m128 sseZInterpolated = InterpolateDepthValues(pMask->m_PrimIdx, ssef0XY, ssef1XY);
// Load current depth buffer contents
__m128 sseDepthCurrent = m_pRenderEngine->FetchDepthBuffer(pMask->m_SampleX, pMask->m_SampleY);
// Perform LESS_THAN_EQUAL depth test
__m128 sseDepthRes = _mm_cmple_ps(sseZInterpolated, sseDepthCurrent);
// Interpolate active vertex attributes
InterpolateVertexAttributes(pMask->m_PrimIdx, ssef0XY, ssef1XY, &interpolatedAttribs);
// 4-sample fragment colors
FragmentOutput fragmentOutput;
// Invoke FS and update color/depth buffer with fragment output
FS(&interpolatedAttribs, m_pRenderEngine->m_pConstantBuffer, &fragmentOutput);
// Generate color mask from 4-bit int mask set during rasterization
__m128i sseColorMask = _mm_setr_epi32(
pMask->m_QuadMask & g_scQuadMask0,
pMask->m_QuadMask & g_scQuadMask1,
pMask->m_QuadMask & g_scQuadMask2,
pMask->m_QuadMask & g_scQuadMask3);
sseColorMask = _mm_cmpeq_epi32(sseColorMask,
_mm_set_epi64x(0x800000004, 0x200000001));
// AND depth mask & coverage mask for quads of fragments
__m128 sseWriteMask = _mm_and_ps(sseDepthRes, _mm_castsi128_ps(sseColorMask));
// Write interpolated Z values
m_pRenderEngine->UpdateDepthBuffer(sseWriteMask, sseZInterpolated, pMask->m_SampleX, pMask->m_SampleY);
// Write fragment output
m_pRenderEngine->UpdateColorBuffer(sseWriteMask, fragmentOutput, pMask->m_SampleX, pMask->m_SampleY);
}После вычисления базисных функций мы сначала интерполируем значения по Z и выполняем тест глубин. Запомнив результат теста глубин, мы интерполируем все остальные пользовательские атрибуты, заданные после VS, передаём их в процедуру FS, которую вызываем следующей, и получаем выходные данные цвета для фрагмента из 4 сэмплов. Для тайлов/блоков у нас есть одна маска записи, которая является результатом теста глубин, потому что мы точно знаем, что все одобренные TA тайлы/блоки видимы. Для четырёхугольнка фрагментов мы также используем маску покрытия для сохранения по маске в буфер кадров значений глубины и цвета. И на этом мы завершаем наше исследование простого тайлового растеризатора.
В заключение
Теперь, когда мы закончили изучение внутренней работы тайлового растеризатора, в голову приходят идеи для экспериментов и его улучшения:
- Поэкспериментировать с конфигурацией растеризатора, попробовать разные размеры тайлов, количество потоков, размер итераций и т.д., чтобы посмотреть, как всё это влияет на производительность
- Замена результатов TR на результаты TA, чтобы увидеть рендеринг тайлов, отброшенных TR
- Инъекция переменной tileIdx в метаданные шейдера и передача её в FS для раскрашиваня частей меша в зависимости от индекса тайла, в котором он рендерится
- Интеграция в конвейер AVX (или даже AVX-512!), чтобы посмотреть, как он влияет на производительность при разных нагрузках (спойлер: я сделал это для AVX, что в большинстве сцен дало рост производительности примерно на 30-50%)
- Нахождение «бутылочных горлышек» для разных сцен и попытка их оптимизировать
- Просто подключение отладчика и пошаговая трассировка треугольников в конвейере
Поэтому я рекомендую всем скомпилировать проекты и попробовать их самостоятельно! Если вы хотите просто посмотреть на них в действии, то найдите пример Hello, Triangle! здесь и пример Scene Rendering здесь (и пакет ресурсов здесь, если вы хотите рендерить более сложные сцены)

Обязательная сцена Sponza из примерно 275k треугольников, отрендеренная на моём ноутбуке с Intel i7 6700-HQ примерно за 60 мс
Справочные материалы
В основном я вдохновлялся/заимствовал/копировал следующие статьи и исследования, поэтому если вы хотите знать больше, то изучите их:
- Rasterization on Larrabee — Adaptive Rasterization Helps Boost Efficiency
- A Modern Approach to Software Rasterization
- Incremental and Hierarchical Hilbert Order Edge Equation Polygon Rasterization
- Triangle Scan Conversion using 2D Homogeneous Coordinates
Автор: PatientZero






