Теория игр — это метод изучения стратегических ситуаций, когда результаты зависят не только от ваших действий, но и от того, что предпримут другие.
Что такое стратегическая ситуация? Вспомним типы рыночных структур: есть совершенная конкуренция, когда все компании являются ценообразующими, то есть им не нужно беспокоиться о стратегии формирования цены, и есть монополия, когда на рынке только одна компания, которая устанавливает свои цены. Так вот: все, что между совершенной конкуренцией и монополией, является стратегической ситуацией.
Алгоритмическая теория игр находится на стыке теории игр и компьютерной науки и направлена на изучение и создание алгоритмов для стратегий.
Под катом короткий рассказ про то, как можно задействовать теорию игр на Python при помощи библиотеки Nashpy.
От редактора: с чего это мы вдруг вспомнили про теорию игр? Все просто — непрерывно модернизируя свою платформу с 900 тысячами участников, мы все время сталкиваемся с ситуациями, где нужно вырабатывать различные стратегии. Например, на портале экспертов НТИ: подтверждать ли всех подряд или, наоборот, не подтверждать никого, а только просить подтверждений. Еще пример: в Точках кипения регулярно наблюдается борьба за ресурсы, и там есть дилеммы — просить ли сразу все оборудование, писать ли реальные числа в количество участников или завышать? При этом решение этих вопросов должно осуществляться с максимальной выгодой для всех.
Nashpy
Как можно догадаться по названию, библиотека предоставляет алгоритмические возможности для достижения равновесия Нэша — набора стратегий для двух игроков, когда каждый из них выбирает наиболее оптимальный вариант своего поведения исходя из аналогичной установки для второго игрока. Отдаленно это напоминает принцип win-win, но с ориентацией на минимальные потери при любом раскладе.
Чтобы разобраться в этой концепции, обратимся к популярной модели «Дилемме заключенного».
Сдать или не сдать
Есть два игрока (заключенные), которые должны решить, сотрудничать ли им друг с другом, не называя имени другого во время допроса в полиции. Полезность такого поведения оценим в три балла для каждого игрока, если оба выберут этот путь. Отправной точкой тут является наказание: если игроки выдадут друг друга, им можно вменить «действие по сговору», то есть «бандитизм», и наказание для них в этом случае будет более строгим, чем если бы они действовали поодиночке.
Если один игрок сдаст другого (при условии, что тот его не сдаст), полезность для него составит четыре балла, для другого игрока — ноль баллов. Если заключенные сдадут друг друга — полезность составит по одному баллу на брата.
Чтобы было легче представить этот набор вариантов, поместим их в табличку, где в ячейках через запятую укажем количество баллов для каждого заключенного в зависимости от сделанного выбора:
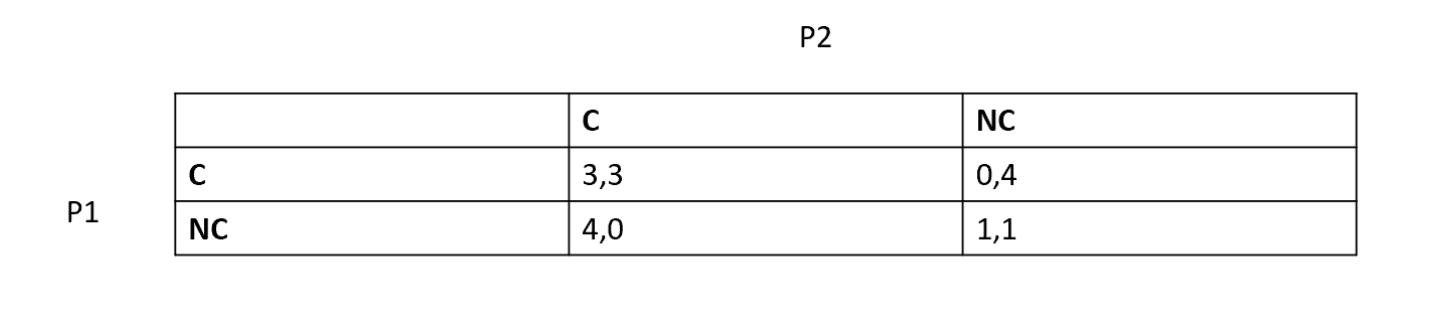
P1 — игрок 1, Р2 — игрок 2, С — сотрудничество, NC — один игрок сдал другого
В итоге оптимальным вариантом для обоих будет сдать друг друга.
Почему заключенные не станут сотрудничать? Рассмотрим стратегию игрока 1 (Р1):
- если игрок 2 (Р2) принимает решение сотрудничать с Р1, лучшая стратегия для Р1 сдать игрока Р2, так как 4>3
- если Р2 принимает решение сдать Р1, то Р1 выгоднее тоже сдать играть Р2, так как 1>0
Итак, выигрышная стратегия для Р1 — (NC; NC), что также справедливо и для Р2. Таким образом, равновесием Нэша будет являться стратегия (NC; NC), когда игроки Р1 и Р2 сдадут друг друга полиции.
Переносим теорию на Python
Для начала нужно установить модуль. Это можно сделать командой pip install nashpy через консоль Jupyter. По окончании установки можно приступить к заданию условий игры. Для двух игроков с ненулевым результатом (что является дефолтным значением в Nashpy) нужно создать две матрицы, отражающие игровые ситуации для каждого игрока. Например, для игрока 1 матрица будет выглядеть следующим образом:
| C | NC | |
| C | 3 | 0 |
| NC | 4 | 1 |
Для игрока 2 вот так:
| C | NC | |
| C | 3 | 4 |
| NC | 0 | 1 |
Воспроизведем это на Python:
import nashpy as nash
import numpy as ns
P1=np.array([[3,0],[4,1]])
P2=np.array([[3,4],[0,1]])
prisoner_dilemma=nash.Game(P1,P2)
prisoner_dilemma
Глядя на эти таблички, мы можем получить оценку полезности взаимодействия игроков. То есть если Р1 не сдает Р2, а Р2 сдает Р1, то значения полезности составят (0, 4). То же самое мы можем получить при помощи матричного вычисления в Nashphy. Примем за сигму вектор действий (их у нас два: сотрудничать или сдать другого заключенного), где значение 0 присваивается всем ячейкам за исключением той, где совершается действие. Тогда для игрока 1 полезность действия будет рассчитываться как:
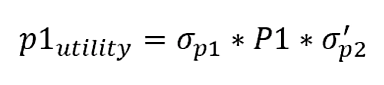
Для игрока 2:
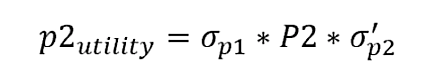
Применив формулу к сценарию, когда игрок 1 выбрал стратегию сотрудничества с другим игроком, а игрок 2 принял решение сдать игрока 1, получим:
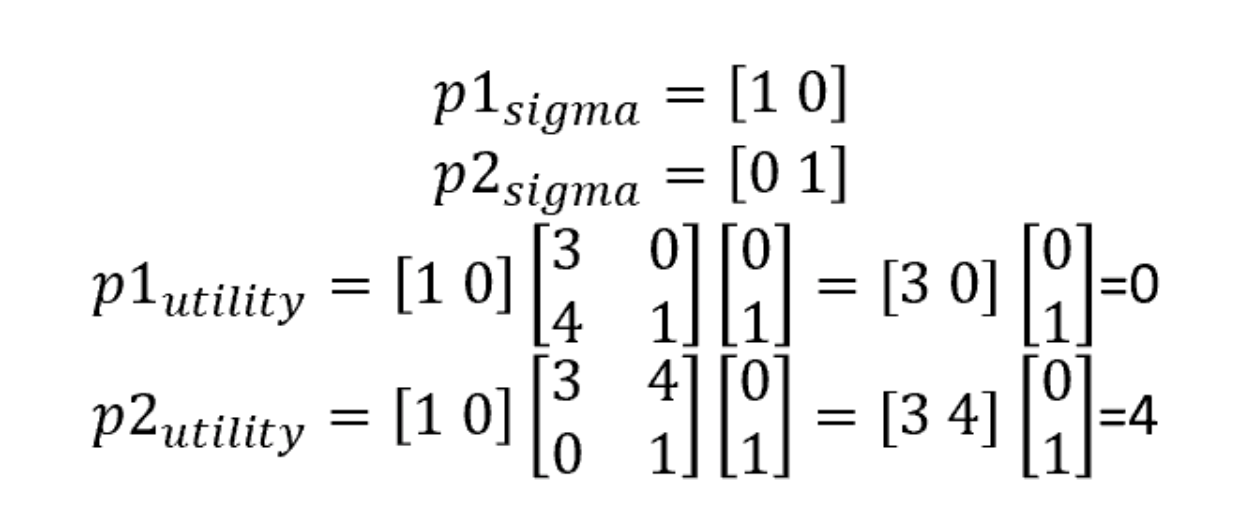
Проверим при помощи Nashpy:

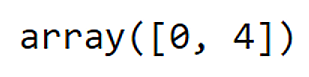
Выясним, найдет ли алгоритм равновесие Нэша, которым, как мы уже выяснили, является (NC; NC):

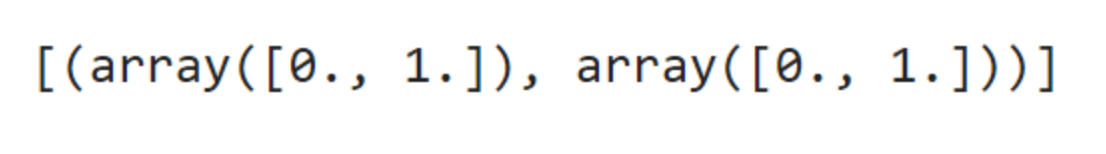
Как можно видеть, равновесие Нэша состоит из двух векторов, каждый из которых отражает действия одного игрока: для игрока 1 это [0; 1], где 1 во втором поле означает, что игрок 1 принял решение сдать игрока 2. Аналогичную картину мы видим и для второго игрока.
P.S. что можно почитать по теме
- Теория игр (Авинаш Диксит и Барри Нейлбафф) — достаточно свежее издание от ИД МИФ. В книге на примерах из кино, спорта, политики и истории авторы показывают, как почти все компании и люди вовлечены во взаимодействия, которые описываются теорией игр.
- Стратегия конфликта (Томас Шеллинг). Книга посвящена исследованию общей логики поведения участников конфликтных ситуаций — теории игр. Вышедшая в 1960 году, она стала фундаментальным вкладом в эту науку, заложив основы теории стратегического поведения.
- Rock, Paper, Scissors: Game Theory in Everyday Life (Len Fisher) — еще одна книга про науку о сотрудничестве. Фишер показывает, как теория игр помогла биологам понять эволюцию сотрудничества в природе, и как мы могли бы применить это в нашем обществе.
Автор: Ekdr





