Туториал по Uplift моделированию. Часть 2

в 12:23, , рубрики: causal effect, causal Inference, causal tree, causality, causalml, data mining, data science, net lift, uplift, аплифт, Блог компании МТС, искусственный интеллект, математика, машинное обучение

Туториал по Uplift моделированию. Часть 2 - 1

В первой части мы познакомились с uplift моделированием и узнали, что метод позволяет выбирать оптимальную стратегию коммуникации с клиентом, а также разобрали особенности сбора данных для обучения модели и несколько базовых алгоритмов. Однако эти подходы не позволяли оптимизировать uplift напрямую. Поэтому в этой части разберем более сложные, но не менее интересные подходы.

Содержание статьи
Трансформация классов
Трансформация классов (регрессия)
Многоклассовая модель
Методы, основанные на деревьях
Заключение
Источники

Трансформация классов

Class Transformation approaсh, Class Variable Transformation approach, Revert Label approach

Достаточно интересный и математически подтвержденный подход к построению модели, представленный еще в 2012 году на ICML [1], который заключается в прогнозировании немного измененной целевой переменной.

$Z_i=Y_i cdot W_i + (1 - Y_i) cdot (1 - W_i)$

где $Z_i$ — новая целевая переменная $i$-ого клиента
$Y_i$ — целевая переменная $i$-ого клиента
$W_i={0, 1}$ — бинарный флаг коммуникации: при $W_i=1$ — $i$-й клиент попал в целевую (treatment) группу, где была коммуникация; при $W_i=0$ — $i$-й клиент попал в контрольную (control) группу, где не было коммуникации.

Другими словами, новый класс равен 1, если мы знаем, что на конкретном наблюдении результат при взаимодействии был бы таким же хорошим, как и в контрольной группе, если бы мы могли знать результат в обеих группах:

Туториал по Uplift моделированию. Часть 2 - 12

Туториал по Uplift моделированию. Часть 2 - 13

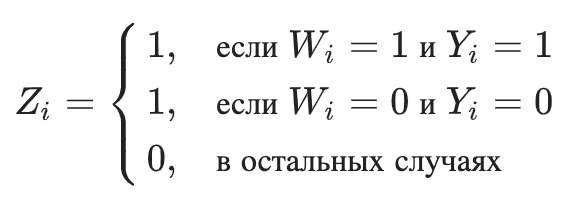
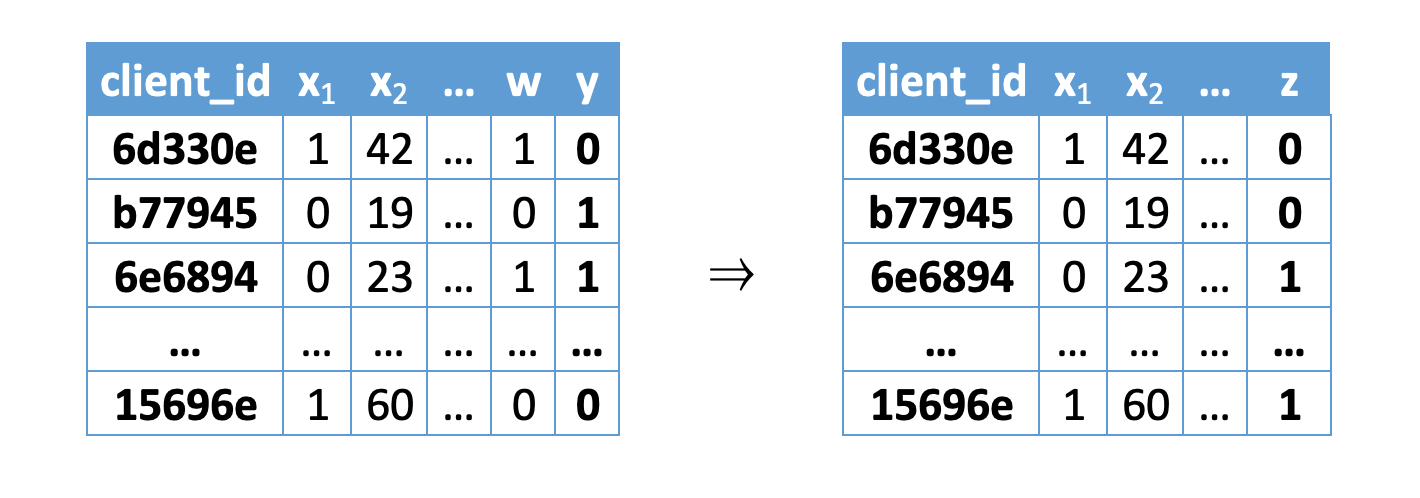
Распишем подробнее, чему равна вероятность новой целевой переменной:

Туториал по Uplift моделированию. Часть 2 - 14

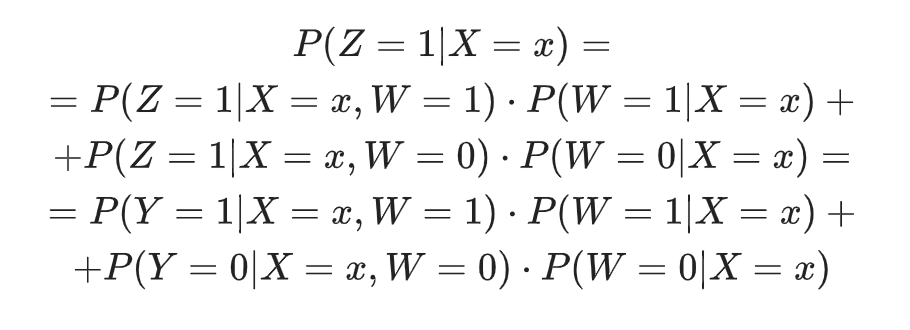
В первой части статьи мы обсуждали, что обучающая выборка для моделирования uplift собирается на основе рандомизированного разбиения части клиентской базы на целевую и контрольную группы. Поэтому коммуникация $W$ не может зависеть от признаков клиента $X=x$. Принимая это, мы имеем:

$P(W | X=x)=P(W) $

Получим:

Туториал по Uplift моделированию. Часть 2 - 18

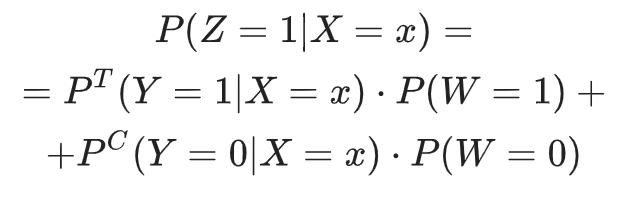
Также допустим, что $P(W=1)=P(W=0)=frac{1}{2}$, т.е. во время эксперимента контрольные и целевые группы были разделены в равных пропорциях. Тогда получим следующее:

Туториал по Uplift моделированию. Часть 2 - 20

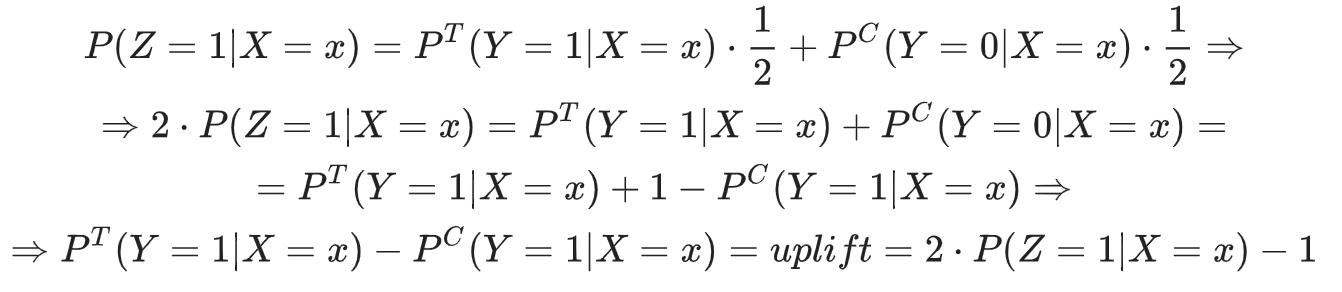
Таким образом, увеличив вдвое прогноз нового таргета и вычтя из него единицу, мы получим значение самого uplift, т.е.

$ uplift=2 cdot P(Z=1) - 1 $

Исходя из допущения, описанного выше: $P(W=1)=P(W=0)=frac{1}{2}$, данный подход следует использовать только в случаях, когда количество клиентов, с которыми мы прокоммуницировали, равно количеству клиентов, с которыми коммуникации не было.

Трансформация классов (регрессия)

Transformed outcome

На предыдущий тип трансформации классов накладываются серьезные ограничения: целевая переменная $Y_i$ может быть только бинарной, а контрольная и целевая группы должны быть распределены в равных пропорциях. Давайте рассмотрим более общий подход из [2], не имеющий таких ограничений.

Трансформируем исходную целевую переменную $Y_i$ по следующей формуле:

$ Z_i=Y_i frac{W_i - p}{p(1 - p)} $

Где $ Z_i $ — новая целевая переменная для $ i $-ого клиента
$ W_i $ — флаг коммуникации для $ i $-ого клиента
$ p $ — propensity score или вероятность отнесения к целевой группе: $ p=P(W_i=1 | X_i=x) $

Здесь важно отметить, что можно оценить $ p $ как долю объектов с $ W=1 $ в выборке. Или воспользоваться способом из [3], в котором предлагается оценить $ p $ как функцию от $ X $, обучив классификатор на имеющихся данных $ X=x $, а в качестве целевой переменной взяв вектор флага коммуникации $ W $.

Туториал по Uplift моделированию. Часть 2 - 38

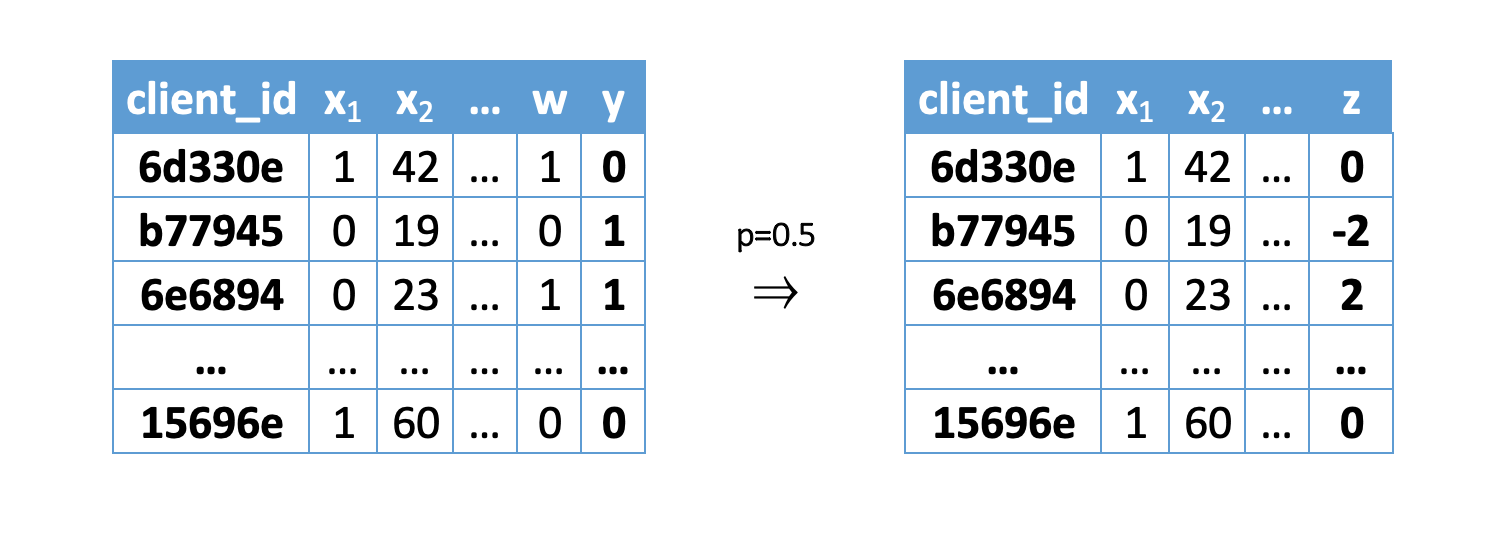
После применении формулы получаем новую целевую переменную $ Z_i $ и можем обучить модель регрессии с функционалом ошибки $ MSE=frac{1}{n}sum_{i=0}^{n} (Z_i - hat{Z_i})^2 $. Так как именно при применении MSE предсказания модели являются условным математическим ожиданием целевой переменной.

Покажем, что условное матожидание трансформированного таргета $ Z_i $ и есть желаемый causal effect из первой части статьи:

$ E[Z_i | X_i=x]=tau_i $

Напомним также, что наблюдаемую целевую переменную можно представить в виде:

Туториал по Uplift моделированию. Часть 2 - 43

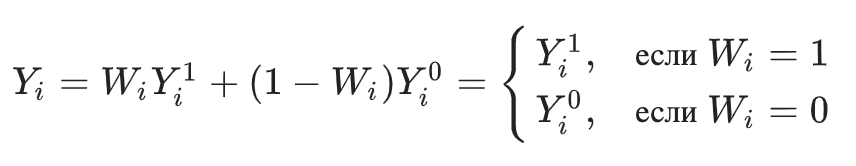
Где $ {Y_i^1, Y_i^0} $ — потенциальные реакции для каждого $ i $-го объекта в зависимости от значения $ W_i $, которые мы хотели бы (но не можем) наблюдать одновременно.

Перепишем формулу трансформации с учетом этого:

$ Z_i=frac{W_i}{p} Y_i^1 - frac{1 - W_i}{1 - p} Y_i^0 $

Тогда:

Туториал по Uplift моделированию. Часть 2 - 48

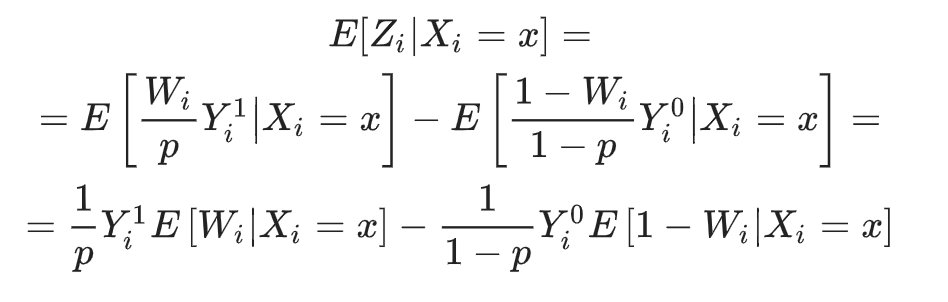
Так как при случайном разбиении на целевую и контрольную группы $ W_i $ не должно зависить от $ X_i $, то:

$ p=P(W_i=1 | X_i=x)=P(W_i=1)=E[W_i] $

Получим, что преобразованная целевая переменная позволяет оценивать uplift:

Туториал по Uplift моделированию. Часть 2 - 52

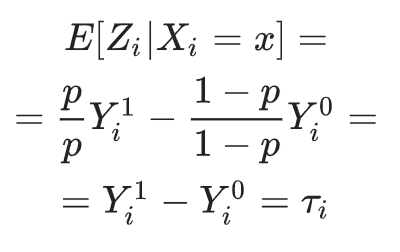
Многоклассовая модель

Generalized Lai Method

Так как мы можем взаимодействовать с клиентами $ W_i={0, 1} $ и наблюдать их реакцию $ Y_i={0, 1} $, то разделим их на 4 непересекающихся класса:

  1. Клиент выполнил целевое действие и мы с ним не коммуницировали (Control Responder — CR): $Y_i=1, W_i=0$
  2. Клиент не выполнил целевое действие и мы с ним не коммуницировали (Control Non-Responder — CN): $Y_i=0, W_i=0 $
  3. Клиент выполнил целевое действие и мы с ним коммуницировали (Treated Responder — TR): $Y_i=1, W_i=1$
  4. Клиент не выполнил целевое действие и мы с ним коммуницировали (Treated Non-Responder — TN): $Y_i=0, W_i=1$

Туториал по Uplift моделированию. Часть 2 - 59
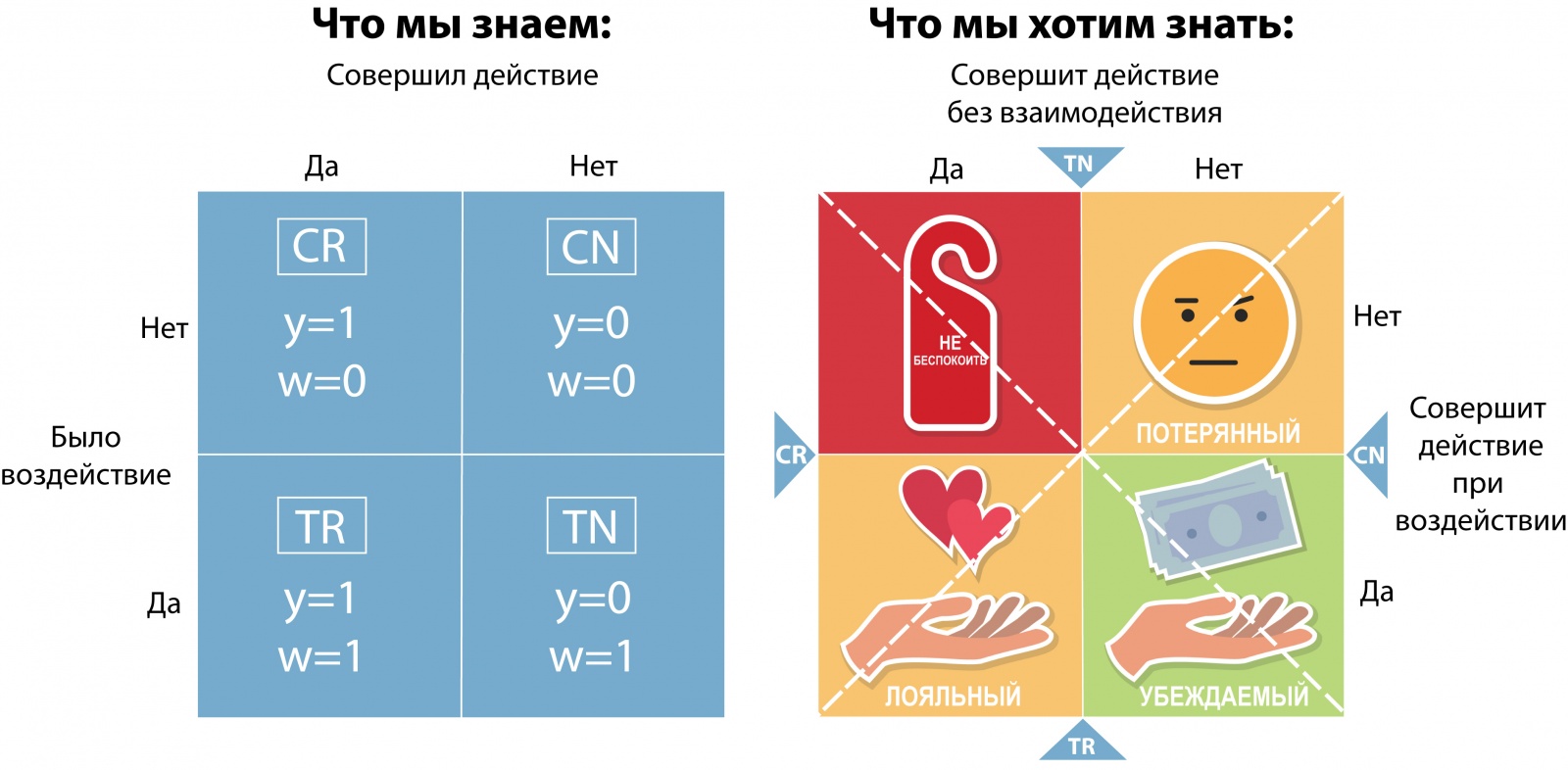
Картинка взята и адаптирована из [4]

Попробуем разобраться, как соотносятся между собой обозначенные выше 4 класса и типы клиентов из первой части, которых мы хотим найти (не беспокоить, потерянный, лояльный, убеждаемый). Их главное различие в том, что классы CR, CN, TR, TN мы можем наблюдать непосредственно по их реакции на коммуникацию, в то время как типы клиентов мы наблюдать не можем. При этом они связаны между собой: каждый из четырех классов может содержат по 2 типа клиента одновременно.

  1. Так как мы не знаем, выполнил бы CR клиент целевое действие при нашем воздействии, то он относится либо к не беспокоить , либо к лояльным клиентам. Проводя аналогичные рассуждения, рассмотрим остальные классы:
  2. среди CN клиентов могут быть как потерянные, так и убеждаемые типы клиентов
  3. Среди TR клиентов могут быть как убеждаемые, так и лояльные типы клиентов
  4. Среди ТN клиентов могут быть как не беспокоить, так и потерянные типы клиентов

В этом подходе [4] предлагается прогнозировать вероятности отнесения клиента к каждому из этих 4 классов и обучить модель многоклассовой классификации:

Туториал по Uplift моделированию. Часть 2 - 60

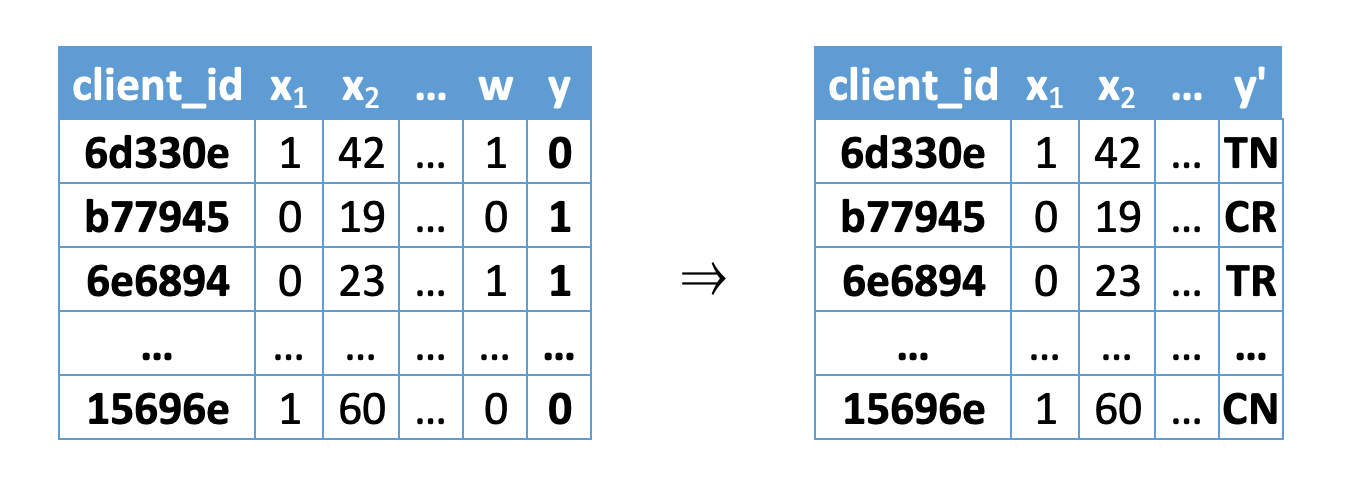
Тогда uplift можно будет рассчитать следующим образом:

$uplift=[P(TR|X=x) + P(CN|X=x)] - [P(TN|X=x) + P(CR|X=x)]$

Мы суммируем вероятности принадлежности к классам $TR$ и $CN$, так как они содержат тип убеждаемый, который мы хотим найти, и вычитаем вероятности принадлежности к классам $TN$ и $CR$, так как они содержат тип не беспокоить, которого наоборот хотелось бы избежать.

Когда выборки по своему объему сильно не сбалансированы, предлагается рассчитывать uplift так:

$ uplift=left[ frac{P(TR|X=x)}{r(T)} +frac{P(CN|X=x)}{r(C)} right] - left[ frac{P(TN|X=x)}{r(T)} + frac{P(CR|X=x)]}{r(C)} right] $

Где $r(T)$ — доля клиентов в тестовой группе, $r(C)$ — доля клиентов в контрольной группе, $r(T)=1 - r(C)$.

Нормировка необходима тогда, когда целевая группа мала по сравнению с контрольной группой, так как в этом случае доля TR и TN клиентов также будет небольшой.

Методы, основанные на деревьях

Decision trees for uplift modeling, Causal trees

Стоит отметить, что предыдущие методы имеют следующие недостатки:

  • В методах с двумя моделями при расчете финального предсказания учитываются результаты двух моделей, а значит их ошибки суммируются;
  • Если для обучения будут использоваться принципиально разные модели или природа данных целевой и контрольной групп будут сильно отличаться, то может потребоваться калибровка предсказаний моделей;
  • Так как во многих методах uplift прогнозируется косвенно, модели могут пропускать слабые различия между целевой и контрольной группах.

Хочется взять хорошо зарекомендовавший себя метод и изменить его так, чтобы непосредственно оптимизировать аплифт. Например, авторы статьи [5] предлагают использовать деревья решений с другим критерием разбиения. Дерево строится так, чтобы максимизировать расстояние (дивергенцию) между распределениями целевой переменной у контрольной и целевой групп. Формально для каждого разбиения это можно записать так:

$ Gain_{D}=D_{afterspace split}(P^T, P^C) - D_{beforespace split}(P^T, P^C) $

Где $ P^C, P^T $ — распределения целевой переменной в контрольной и целевой группах
$ D $ — дивергенция (расхождение) между двумя распределениями

Есть несколько видов дивергенции D, которые используют для решения этой задачи:

  • Дивергенция Кульбака—Лейблера (Kullback–Leibler divergence):

    $ KL(P, Q)=sum_i p_i log frac{p_i}{q_i} $

  • Евклидово расстояние (Euclidean distance):

    $ E(P, Q)=sum_i (p_i - q_i) ^ 2 $

  • Дивергенция хи-квадрат (Сhi-squared divergence):

    $ chi^2(P, Q)=sum_i frac{(p_i - q_i)^2}{q_i} $

Где распределения представлены как $ Q=(q_1, ..., q_n) и P=(p_1, ..., p_n) $

Если получается так, что в вершине при разбиении остаются объекты одной группы (контрольной или целевой), то дивергенция сводится к стандартному для деревьев критерию (KL-дивергенция — к энтропийному критерию, Евклидово расстояние и хи-квадрат — к критерию Джини).

Также важное условие разбиения — это сведение к минимуму разницы между количеством объектов, попавших в левую и правую дочернюю вершину. Слева на картинке изображен пример плохого разбиения, когда высокое значение величины uplift в левой дочерней вершине достигается за счет того, что в него попало всего 30 объектов из 1000.

Туториал по Uplift моделированию. Часть 2 - 77
Картинка взята и адаптирована из [7]

Чтобы контролировать количество объектов в разбиении, можно воспользоваться формулой взвешенной дивергенции (после разбиения):

$ D_{weighted}(P^T, P^C)=frac{n_L cdot D(P_L^T, P_L^C) + n_R cdot D(P_R^T, P_R^C)}{n_L + n_R} $

Где $ n_L $ и $ n_R $ — количество объектов, попавших в левую и правую дочернюю вершину соответственно
$ P_L^T, P_L^C, P_R^T, P_R^C $ — распределения целевой переменной в целевой и контрольной группе для левой и правой дочерних вершин

После реализации дерева с новым критерием разбиения можно использовать этот алгоритм в качестве базового алгоритма в ансамблях, например, в случайном лесе или градиентном бустинге, а также применять стандартные для деревьев методы борьбы с переобучением, такие как стрижка (pruning) или ранняя остановка (early stopping).

Заключение

Цикл обзорных статей не раскрывает всех подходов к прогнозированию uplift, однако охватывает наиболее популярные и интересные для нас. На сегодняшний день не существует идеального метода, который на разных данных и на протяжении долгого времени выигрывал бы по качеству у других. Этот факт мотивирует исследователей разрабатывать новые подходы (например, любопытная статья 2019 года о применении бандитов к решению данной задачи [8]). В дальнейшем мы планируем рассмотреть метрики качества для оценки прогнозируемого uplift.

Uplift моделирование используется не только для задач маркетинга, но и в медицине, политике, экономике и в других сферах. То есть, когда поведение объектов может изменяться под некоторым контролируемым воздействием, такой подход может быть более предпочтительным, чем другие.

Статья написана в соавторстве с Максимом Шевченко (maks-sh)

Источники

  • [1] Maciej Jaskowski and Szymon Jaroszewicz. Uplift modeling for clinical trial data. ICML Workshop on Clinical Data Analysis, 2012.
  • [2] Susan Athey and Guido W Imbens. Machine learning methods for estimating heterogeneouscausal effects. stat, 1050:5, 2015.
  • [3] P. Richard Hahn, Jared S. Murray, and Carlos Carvalho. Bayesian regression tree models for causal inference: regularization, confounding, and heterogeneous effects. 2019.
  • [4] Kane, K., V. S. Y. Lo, and J. Zheng. Mining for the Truly Responsive Customers and Prospects Using True-Lift Modeling: Comparison of New and Existing Methods. Journal of Marketing Analytics 2 (4): 218–238. 2014.
  • [5] Piotr Rzepakowski and Szymon Jaroszewicz. Decision trees for uplift modeling with single
    and multiple treatments. Knowledge and Information Systems, 32(2):303–327, 2012.
  • [6] Yan Zhao, Xiao Fang, and David Simchi-Levi. Uplift modeling with multiple treatments and general response types. In Proceedings of the 2017 SIAM International Conference on Data Mining, 588–596. SIAM, 2017.
  • [7] Wouter Verbeke, Bart Baesens, Cristian Bravo. Profit Driven Business Analytics: A Practitioner's Guide to Transforming Big Data into Added Value.
  • [8] Jeroen Berrevoets, Sam Verboven, Wouter Verbeke. Optimising Individual-Treatment-Effect Using Bandits, 2019.

Автор: iraelisova

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js