Моделирование бега под дождем
Вступление
Все началось с чрезвычайно провокационного, граничащего с дерзостью заявления, которое категорически не соответствует моим представлением об окружающем мире: «Можно меньше промокнуть, если бежать под дождем – это миф». Другими словами, из этого утверждения следует, что общеизвестным и общепринятым является тот факт, что бегущий под дождем человек промокнет сильнее, чем такой же человек прошедший пешком такое же расстояние, под тем же дождем. Но, какие-то, непроверенные не заслуживающие доверия источники утверждают обратное, что если вы побыстрее уберетесь из под дождя то промокните меньше.
Это заявление прозвучало в телепрограмме Mythbusters (эпизод 001). Я несколько раз перепроверял — формулировка мифа именно такая: «A person will end up drier by running in the rain rather than walking».
Более того, результатом проверки оказалось разрушение этого мифа, то есть, ведущий, который бежал, промок сильнее ведущего, который шел!? То есть эти непроверенные и не заслуживающие доверия источники, со своими глупостями были поставлены на место. До того момента, в моем мире все было наоборот, и, чтобы меньше промокнуть, я старался бегом добраться до укрытия.
Далее, пару сезонов спустя, этот миф был перепроверен и опровергнут (эпизод 38). Но результаты и в первом и во втором случае оказались не очень показательными: разница собранной воды была небольшой, и вряд ли сильно отличалась от статистической погрешности, и от погрешности измерений на весах. В первом эксперименте дождь создавался путем подачи воды на разбрызгиватели, которые были подвешены под потолок высокого ангара. Во втором эксперименте работали с тем, что упадет с неба. После второго эксперимента ясности стало еще меньше.
Первый эксперимент мне понравился больше, так как там были контролируемые условия, причем эти условия можно было поддерживать необходимое время. В случае с обычным дождем условия постоянно меняются – дождь может прекратиться, измениться его интенсивность или подует ветер. На мой взгляд, нужно было продолжить первое исследование: можно было увеличить дистанцию, можно было поиграть с параметрами дождя чтобы сократить статистическую погрешность и сделать результаты более убедительными. Mythbusters — отличная телепрограмма, но в этом конкретном случае хотелось взять и все переделать. Особенно заинтересовала тема влияния характера дождя, на итоговое промокание, ведь обычно в таких экспериментах идет усредненный дождь, а ведь дождь бывает разный.
Как это обычно бывает, я мужественно преодолел это бессмысленное, навязанное желание переделать эксперимент и забыл о нем. Но лето в этом году в московском регионе как то слишком часто располагало к размышлениям на тему «так все-таки убегать ли мне от этого дождя, или идти спокойно». В результате решил написать небольшой проект и поисследовать, то, что было интересно, с помощью компьютерного моделирования. Как оказалось, в Московском регионе тема остается актуальной и сейчас в декабре.
Со следующего раздела приводится описание того, что получилось, но здесь нужно сказать несколько слов, про историю вопроса. При подготовке статьи выяснилось, что вопрос «идти или бежать под дождем» не дает покоя множеству гиков по всему свету уже довольно давно. Видимо, первым поднял волну, известный популяризатор науки Яков Исидович Перельман, в его книге «Занимательная механика» (видел только 4е издание 1937г., но возможна задача была и в более ранних начиная с 1930 г.) В девятой главе «Треняе и сопротивление среды» (да тренЯе, начало двадцатого век все — таки) последний раздел называется «Когда дождь промочит сильнее?», но фактически задача звучит так «В каком случае вы больше промочите свою шляпу?». Тут есть разница — в книге речь идет только о той составляющей дождя, которую шляпа воспринимает сверху, о столкновении с дождем в вертикальной плоскости речи не идет. К тому же в задаче эксперимент проводится при одинаковом времени, пребывания под дождем, в то время как нас интересует одинаковое расстояние. Нет никаких сомнений в справедливости, приведенного в книге решения, но само название раздела, и самостоятельные выводы читателей могли привести к неправильным выводам и появлению стереотипа.
После Перельмана были статьи в научно-популярных журналах древних и не очень, потом видосы вот, и вот перевод даже есть на хабре вот здесь. Еще одна статья, мимо которой трудно пройти – это статья 2012 года итальянского физика Франко Боччи в European Journal of Physics, саму статью, вряд ли читало большое количество людей, но про нее очень много писали в СМИ, например вот интересно написано, на мой взгляд. Есть и другие исследования разной степени серьезности. Оказалось, что история этой проблемы, возможно не менее интересна, чем сама проблема, и, возможно может быть предметом отдельной статьи.
Моделирование
Ограничения и допущения
Суть моделирования – это целенаправленное упрощение и абстрагирование восприятия реальности. Представленная в статье модель — не исключение. Далее в тексте могут быть указания, на то, что та или иная особенность, обусловленная спецификой задачи, физическими, когнитивными ограничениями, а также ограничениями связанные религиозными, расовыми, политическими, сексуальными и прочими предпочтениями автора, является допущением или ограничением (другими словами те вещи, которые было не только лень делать, но еще и лень объяснять, почему я их не сделал).
Примеры ограничений и допущений: Количество капель в ячейке одна (ограничение на максимальную интенсивность), все капли имеют одинаковый размер, предполагается что человек во время ходьбы и бега не машет руками и ногами (площадь фронтальной и горизонтальной проекции всегда одинакова), вода поднятая с ботинок на спину не учитывается, ветра в эксперименте нет и пр.
Пространство и человек

Пространство
Модель представлена двумя объектами пространство и человек.
Пространство – это прямоугольный параллелепипед, разбитый на кубики размером 1х1х1 см.
Ширина пространства равна ширине человека: в проведенном эксперименте не рассматриваются случаи с ветром, и с боковым ветром, поэтому обсчитывать пространство за пределами ширины человека нет никакого смысла.
Высота пространства больше высоты человека на один горизонтальный слой кубиков – то есть на один сантиметр, в этом слое начинают регистрироваться капли, которые в следующий момент времени упадут на человека, или дальше в пространство не занятое человеком.
Длина (протяженность) пространства – должна быть равна длине дистанции, но это очень неэкономично, так как для эксперимента нужно знать только о состоянии пространства над человеком, и о нескольких слоях перед ним. Поэтому в проекте пространство используется циклично, а его длина выбирается такой, чтобы к моменту, когда человек полностью его пройдет в первом вертикальном слое обновились все ячейки. Другими словами капля, которая появилась в слое, находящимся сразу за спиной человека должна иметь достаточно времени, чтобы упасть на землю, к тому моменту, когда человек вновь приблизится к этому слою лицом. Таким образом, при правильном подборе длины пространства на человека всегда будут капать свежие капли.
Нужно отметить, что при проведении эксперимента длина пространства устанавливается единожды, и далее не меняется, поэтому для начальной установки значения длинны, выбиралось такое соотношение параметров, чтобы во всех случаях длина была достаточная (максимальная скорость человека и минимальная скорость падения капель).
Пространство для эксперимента можно вообразить по разному, например как замкнутый коридор, но мне больше нравится представлять его прямоугольным пятном света, от фонаря, который светит с боку на человека, и которое движется вместе с человеком. Каждая капля, которая попадает в свет внутри пятна, регистрируется. Такой подход позволяет отделить понятие физического, бесконечного пространства, в котором под дождем бегает человек, от пространства эксперимента — воображаемой трехмерной сетки, состояние каждой ячейки которой проверяется в каждый момент времени эксперимента. В статье слово «пространство» используется во втором значении.
В программе пространство представлено трехмерным байтовым массивом. Индексы элемента в массиве соответствуют координатам ячейки в пространстве (протяженность, высота, ширина), сам элемент описывает состояние. Состояния может быть только два – в ячейке есть капля дождя или ячейка пустая.
Пространство также можно представить как набор горизонтальных слоев, сквозь которые падает дождь, и как набор вертикальных слоев с которыми, двигаясь, сталкивается человек. В программе, есть классы – обертки, отвечающие за эти представления.
Человек
Человек в проекте – это просто прямоугольный параллелепипед. Для эксперимента в первую очередь нам интересны его проекция на горизонтальную плоскость для подсчета капель, падающих сверху, и проекция на вертикальную плоскость, перпендикулярную направлению движения, для подсчета капель с которыми человек сталкивается, двигаясь вперед. Также используется координата, отвечающая за его положение в пространстве, и счетчики собранной воды спереди и сверху.
Для того, чтобы оценить площадь горизонтальной проекции погуглил, одна из первых ссылок была на какой-то нормативный акт, который использует МЧС. Там горизонтальная проекция человека представлена эллипсом с размерами осей 0,5 м (ширина человека в плечах) и 0,25 м (толщина человека). Похоже на правду, поэтому взял прямоугольник почти такой же площади (S эллипса=pi*a*b S = 3.14*(50/2)*(25/2) ~ 982 кв. см, прямоугольник 48 на 20 = 960 кв. см). Как было показано выше, эти данные используются, в том числе для определения ширины и протяженности пространства. Определения вертикальной проекции человека не нашел, поэтому для роста взял величину чуть меньше среднего - 160 см. Размерность человека легко меняется в проекте, но эксперимент проводился только на одном наборе параметров. Так как, этот вопрос показался мне не очень интересным – во первых во время дождя вряд ли на эти параметры можно как-то повлиять, а во вторых выяснение того, какое телосложение оптимально для промокания под дождем может показаться кому-то обидным. Отношу это к ограничениям и допущениям.
Скорость человека: за нижний предел взята скорость 2,196 км/ч взята вот отсюда видимо эти данные используются для целей протезирования, верхний предел — 43.9 км/ч — самая быстрая на данный момент зафиксированная скорость бега.
Про дождь
Дождь в проекте это процесс, который происходит в пространстве, и который имеет свои характеристики: размер капли, скорость падения, интенсивность.
По данным Википедии диаметр дождевой капли не может быть меньше 0.5 мм, так как это будет уже не дождь, а морось, и не больше 6-7 мм, при таких условиях капли распадаются на более мелкие.
В соответствии с той же статьей скорость падения капель варьируется от 2 до 6 м/с для мелких капель и от 9 до 30 м/с для капель с диаметром 5 мм. При размере от 5мм до 7мм скорость падения снижается из-за того, что такие крупные капли приобретают форму парашюта, и сопротивление воздуха растет. Скорость падения капель зависит не только от размера самой капли, но и от условий в которых она падает – предполагаю, что от плотности воздуха, наличия восходящих или нисходящих потоков, и пр.
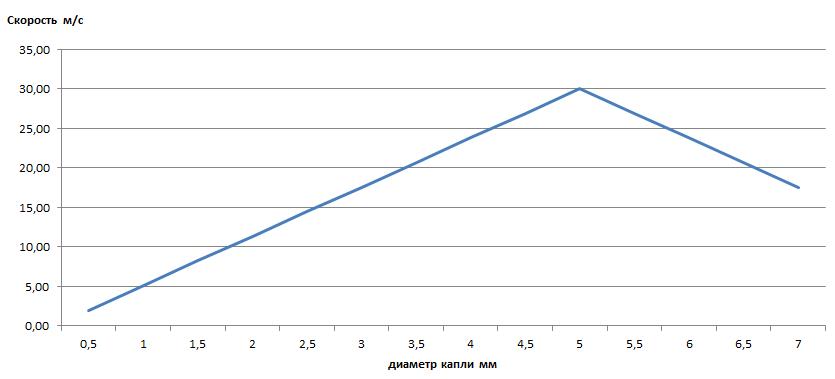
В проекте установлена линейная зависимость скорости падения от длины диаметра: в диапазоне диаметров от 0.5 до 5 мм скорость линейно возрастает от 2м/с до 30 м/с (DropSize*6.22 – 1.11), в диапазоне от 5 мм до 7 мм скорость снижается с той же интенсивностью ((10 — DropSize)*6.22 – 1.11), за пределами диапазона 0.5 – 7 мм эксперимент не проводится.
Линейная зависимость, используемая в эксперименте, не противоречит существующей картине мира, но она ограничена, и поэтому является допущением. К примеру, размеру капли 5мм в проекте соответствует скорость 30 м/с – в реальном мире такое вполне может быть (если верить Википедии), но в реальном мире также возможно, что капля диаметром 5мм будет падать гораздо медленнее — со скоростью 9 м/с. Если кто-то заинтересуется и решит сам поэкспериментировать, то можно изменить зависимость на любую другую, или даже поэкспериментировать с несколькими. В данном проекте эта фича будет использована в очень ограниченном объеме (из – за нехватки времени).
Интенсивность – еще одна интересная, и важная характеристика дождя. Интенсивность обычно указывается в миллиметрах в час. Один миллиметр в час означает, что за один час на горизонтальную поверхность площадью один квадратный метр выпадет слой воды толщиной один миллиметр. Не трудно посчитать, что объем этого слоя воды – один литр. То есть один мм/ч это то же самое что один литр на один квадратный метр за один час. Иногда в прогнозах погоды, когда хотят описать масштаб бедствия, указывают просто миллиметры — это уже посчитанная высота слоя воды, выпавшей за всю продолжительность дождя. В проекте, и далее в статье будет использоваться единица измерения — миллиметры в час.
В соответствии с Википедией интенсивность дождя обычно составляет от 0,25 мм/ч (моросящий дождь) до 100 мм/ч (ливень) – эксперимент проводился в границах этих значений.
Про распределение капель в пространстве:
Есть один интересный момент, на котором хотелось бы ненадолго остановиться. На стадии проектирования планировалось, что верхний горизонтальный слой, будет заполняться каплями следующим образом: один раз вычисляется вероятность появления капли в ячейке, а затем, перебирая все ячейки слоя, рандомайзер, исходя из этой вероятности, будет помещать в ячейку каплю, или не помещать. Вероятность вычислялась как отношение необходимого количества капель в слое к общему количеству ячеек в слое. С учетом того, что пространство и так сокращенно до минимума такой подход представлялся вполне разумным. Однако перед началом эксперимента решил оценить количество капель на единицу пространства (ту самую веросятность появления) и вот что получилось: Ниже представлены графики количества капель в слое площадью один квадратный метр и толщиной один сантиметр, в зависимости от размера капли, каждый график соответствует своей интенсивности:
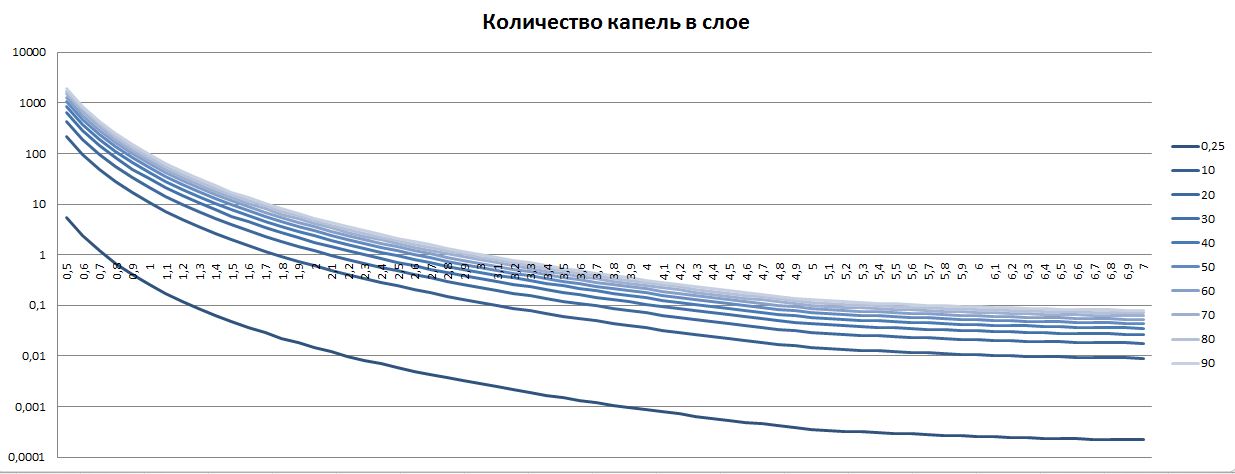
По горизонтальной оси – размер капли, по вертикальной оси – количество капель. Вертикальная ось – логарифмическая, так как разброс количества капель очень большой. Такой большой разброс объясняется тем, что объем капли пропорционален третьей степени от ее линейных размеров (диаметра), плюс с увеличением размера капли увеличивается скорость ее падения. Соответственно при небольшом изменении диаметра капли количество капель в объеме меняется очень сильно (например, для интенсивности дождя 80 мм/ч, при диаметре капли 0.8 мм требуется около 215 капель на слой, а при увеличении диаметра капли в два раза – до 1.6 мм, всего 12 капель на слой).
Теперь, что касается оптимизации: как видно из графиков даже при минимальном объеме капли и максимальной интенсивности количество капель на 10 тысяч ячеек – не превышает 2 х тысяч, в большинстве случаев количество капель менее 100, а при размере диаметра капли более 3мм количество капель на слой меньше одной. Соответственно перебирать каждую ячейку слоя, чтобы в конечном итоге в нем оказалась только одна капля не экономично. Более экономичный вариант – вычислить количество капель в слое, а затем случайным образом разбросать их по слою. Единственное усложнение — это случай, когда выбранная ячейка оказывается уже заполненной (в этой ситуации красиво смотрится рекурсия). Если к этому всему добавить запоминание заполненных ячеек, для последующей очистки слоев, то можно получить значительную экономию по CPU, при незначительном увеличении использования RAM.
Процесс эмулирования дождя
Процесс моделирование происходит в одном главном цикле. Каждая итерация этого цикла соответствует минимальному интервалу времени (тик). Каждый тик состояние системы обновляется и фиксируется. Продолжительность тика соответствует продолжительности пролета капли дождя через один слой пространства (в нашем случае 1см), поэтому один тик в программе может соответствовать различным интервалам времени в реальной жизни, в зависимости от входных параметров (а точнее от скорости падения капель). Ниже описаны действия, происходящие внутри каждой итерации:
Процесс дождя в проекте выглядит следующим образом: сначала верхний слой случайным образом заполняется каплями (см. раздел выше), пусть это будет слой номер n. В следующей итерации капли из n-го слоя проваливаются в ячейки слоя, расположенного прямо под ними — в слой номер n-1, верхний слой снова заполняется. Далее все происходит аналогично: в слой номер n-2 проваливаются капли слоя n-1, в слой n-1 капли n-ного, а n-ный снова заполняется случайным образом, и так далее. Когда капли, достигнут самого нижнего слоя, они никуда не проваливаются, а просто исчезают (скажем, падают на землю, и впитываются), и далее, после очистки, этот слой поднимается наверх и переиспользуется.
Перебор каждой ячейки пространства для того чтобы скопировать (опустить ниже) все капли, выполняющийся в каждой итерации довольно затратная операция. Для того чтобы оптимизировать этот процесс, в классе пространства есть указатель, этот указатель циклически перемещается по номерам горизонтальных слоев (каждую итерацию он инкрементируется на единицу). Номер слоя соответствующий указателю на данной итерации считается верхним. Технически изменяется указатель, но, как известно, движение относительно, и если привязать систему отсчета к указателю, то данный процесс можно представить себе как движение (вертикальное падение) стопки горизонтальных слоев мимо неподвижного указателя, на котором отражается номер того слоя, который в данный момент пролетает мимо него.
Процесс эмулирования движения человека
В классе человека есть указатель, который циклически перемещается по вертикальным слоям, перпендикулярным направлению движения (фронтальные слои), этот указатель указывает на слой, расположенный перед самым его носом, и используется для определения пятна на верхнем слое, капли из которого падают на человека сверху.
В программе также есть переменная (число с плавающей точкой), которая отражает точное текущее положение человека (пройденное расстояние). Зная скорость падения капель, можно вычислить время соответствующее одному тику. Умножив продолжительность тика на скорость человека, получаем расстояние, проходимое человеком за один тик. Каждую итерацию пройденное расстояние инкрементируется на расстояние, проходимое за один тик. Если человек остается в том же слое — указатель на вертикальный слой не инкрементируется, счетчик воды собранной спереди никак не изменяется. Если человек переходит в следующий слой, указатель на вертикальный слой инкрементируется на единицу, а счетчик воды собранной спереди увеличивается на количество капель, находящихся в данный момент в вертикальном слое, на который указывает указатель. Если человек за один тик проходит несколько слоев, то счетчик увеличивается на количество капель находящихся во всех пройденных слоях, а указатель инкрементируется на число пройденных слоев.
Счетчик капель, упавших сверху обновляется каждый тик, без исключения. Как было указанно выше, расположение пятна, из которого капли попадут на человека, определяется указателем на фронтальный слой.
Собственно про модель, и про то, как она работает все сказано, далее предлагаю перейти к экспериментам.
Эксперименты и выводы
Цели и задачи
Перед экспериментом предлагаю определить и формализовать вопросы, ради которых все затевалось.
Первый, и самый главный вопрос – «Правда ли, что можно меньше промокнуть под дождем, если идти, а не бежать до укрытия?» Более формально – «Как влияет скорость человека на итоговый объем собранной воды при прочих равных условиях?»
Второй. Если на первый вопрос будет дан ответ «нет», но мы то знаем, что разрушителям легенд удалось воспроизвести ситуацию, когда бегущий человек промок сильнее пешехода, то возникает вопрос: Возможна ли ситуация, когда бегущий человек промокнет сильнее идущего и при каких условиях это возможно?
Третий. «Как влияет размер капель на итоговый объем собранной воды при прочих равных условиях?»
Четвертый. «С какой стороны человек соберет больше воды – сверху, или спереди? От чего зависит это соотношение?»
Определение понятий
Для удобства описания необходимо определить несколько понятий, иначе будет легко запутаться. Итак: далее человека буду называть Катя, это немного сократит объем текста, и добавит в рассказ еще больше веселья, угара и легкомыслия. В эксперименте Кате нужно будет проходить или пробегать расстояние в 1 километр, одно прохождение дистанции от начала до конца будет называться забег.
Далее, для того, чтобы оценить влияние скорости на объем собранной воды Кате нужно при одних и тех же условиях сделать несколько забегов с разными скоростями. В нашем случае это будут скорость медленного прогулочного шага 2,2 км/ч, скорость быстрого бега 23,04 км/ч, и скорость самого быстрого бега, которую только способен развить человек 43,88 км/ч. Все три забега вместе буду называть сетом. То есть один сет – это три забега с разными скоростями, но при совершенно одинаковых параметрах дождя.
Далее, так как нас интересует влияние характера дождя, нужно попросить Катю пробежать несколько сетов при разных условиях. Модель предоставляет возможность влиять на две характеристики дождя – размер капли и интенсивность, для удобства их можно организовать иерархически, например, размер капли будет более низким звеном по отношению к интенсивности. Тогда Кате нужно будет пробежать несколько сетов с разным размером капель, но постоянной интенсивностью. Так как сет сетов не самое благозвучное название буду называть его суперсетом, хотя тоже не огонь. Ну и на самом верхнем уровне иерархии у нас будет интенсивность, которая включает несколько мегасетов при разной интенсивностью, этот сет суперсетов буду называть серией. Всего размеров капель будет четыре: почти минимальная (0.6 мм), максимальная (7 мм), соответствующая максимальной скорости 5 (мм) и «средняя» (1.4 мм). Последний размер примерно соответствует распределению капель 10 штук на один квадратный метр почти во всем диапазоне интенсивностей (10 – 100 мм/ч). Интенсивностей будет три 1, 50 и 100 миллиметров в час (минимальная, средняя, и максимальная). Для наглядности иерархия приведена в таблице ниже. Но, так как каждому забегу соответствует одна запись в базе, то в дальнейшем нам ничего не будет стоить перегруппировать и изменить иерархию по своему усмотрению.
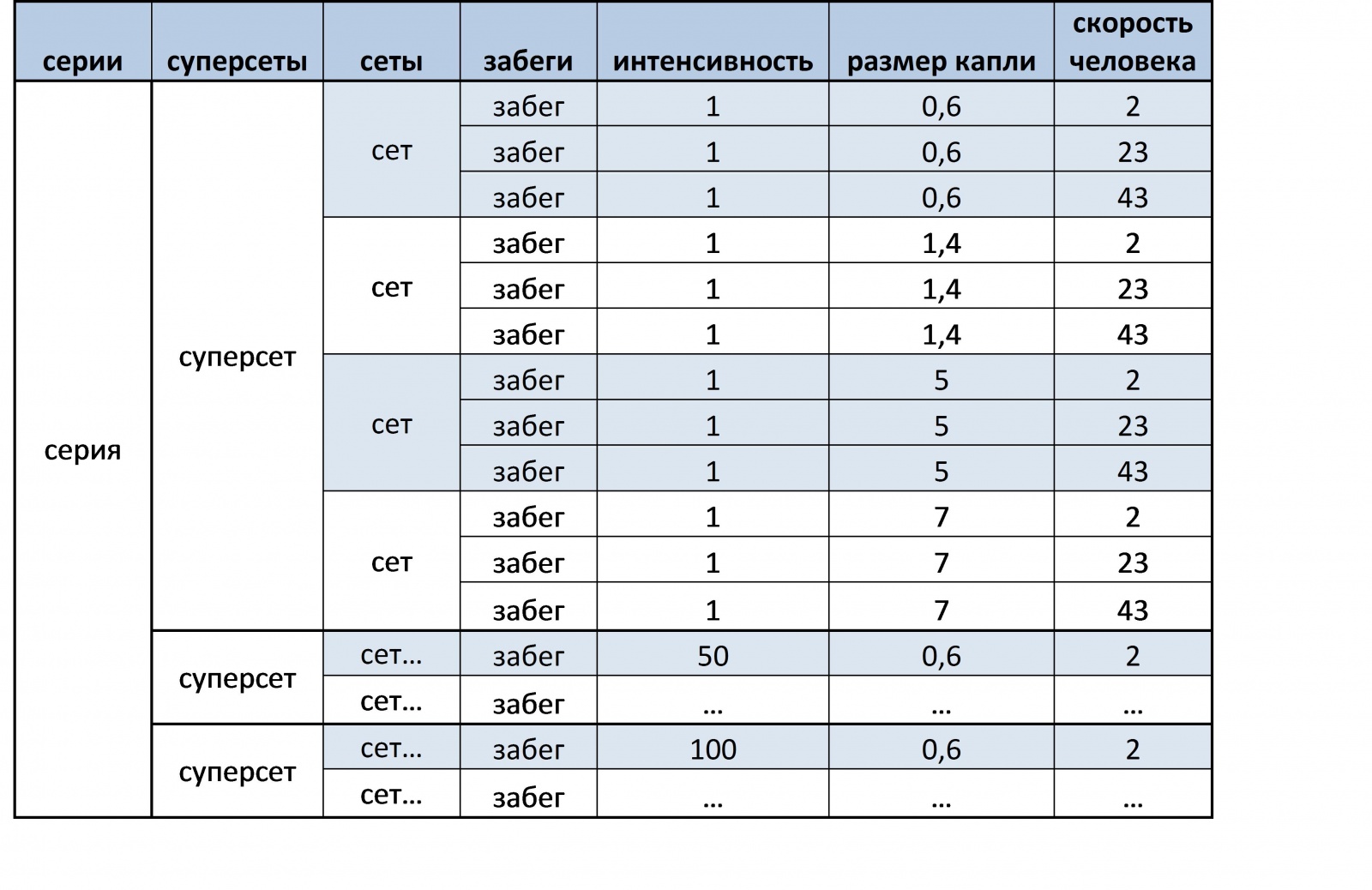
Во время проведения эксперимента будут сниматься следующие показатели:
для каждого забега:
— объем полученной воды;
— количество капель всего;
— количество (объем) капель сверху;
— количество (объем) капель спереди;
— средний прирост за один тик;
— средний прирост сверху за один тик;
— средний прирост за одно горизонтальное смещение (всего / только горизонтальные/ только фронтальные)
для каждого сета
— разница полученного объема на разных скоростях.
— другие показатели, которые придут в голову.
Результаты и выводы
Итак, первый эксперимент прошел. Он состоял из одной серии, трех суперсетов, 12 сетов, и 36 забегов на дистанцию 1 км. Всего в базу было сделано 32 529 927 записей, время выполнения на моей чахлой машине чуть больше 2 часов. Ниже сводная таблица, уже после обработки результатов, в которой приведен общий объем полученной воды в каждом забеге, и параметры забегов.

В последнем столбце приведена разница собранной воды от забега к забегу в каждом сете. Напомню, что в одном сете забеги отличаются только скоростью прохождения дистанции. Как видно в последнем столбце нет ни одного отрицательного числа, соответственно ответ на первый вопрос: «Как влияет скорость человека на итоговый объем собранной воды при прочих равных условиях?» Ответ: Итоговый объем собранной воды всегда меньше при большей скорости движения человека. Проведенный эксперимент наглядно это демонстрирует.
Тут, казалось бы, должен быть очевидный ответ на второй вопрос «Возможна ли ситуация, когда бегущий человек промокнет сильнее идущего и при каких условиях это возможно?» — нет, не возможно, и разрушители что-то накосячили. Но давайте посмотрим на третий сет:

Разница собранной воды при быстром беге и очень быстром беге (отличие 20 км/ч) на дистанции 1 километр, дало очень небольшое преимущество 3.2 мл в абсолютном выражении и ~ 26% в относительном. Для справки, распределение капель в пространстве при такой интенсивности и при таком диаметре очень небольшая: вероятность появления капли в слое равна 0,0005841873 или 1 капля на 1712 слоев, или 1 капля на 7,06 кубических метров. Так как появление капли в том или ином месте – это случайный процесс, и если сократить разницу в скоростях, и дистанцию, то результаты станут более случайными, в этом случае возможно всякое, в том числе более сильное промокание на более низкой скорости см. таблицу ниже.
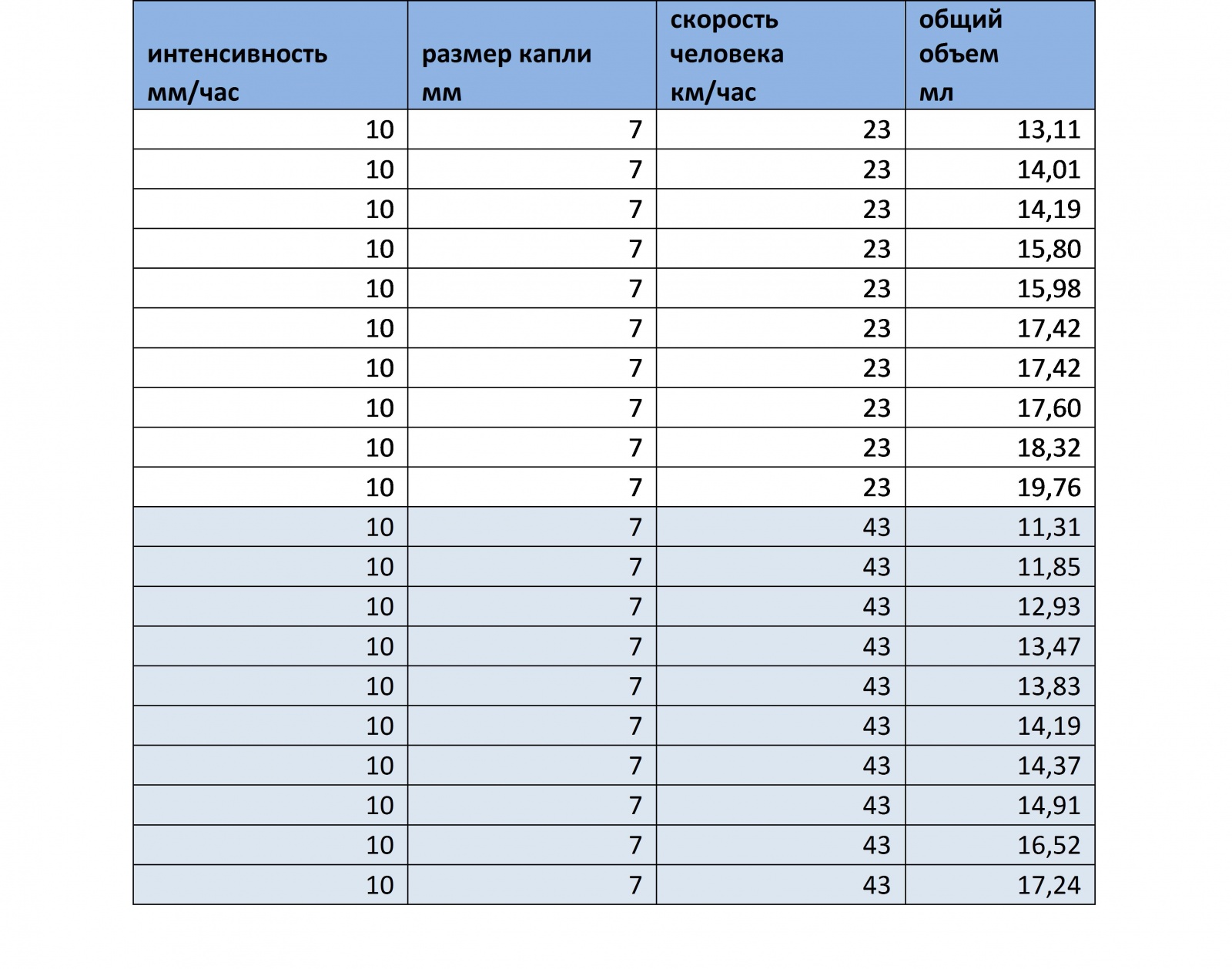
Эта таблица отражает результат дополнительных 20 забегов на короткую дистанцию 100 м, с небольшой интенсивностью и крупными каплями дождя. Как видно диапазон значений собранной воды на скорости 23 км/ч частично пересекается с диапазоном значений собранной воды на скорости 43 км/ч. Это означает, что ответ на вопрос о том, можно ли собрать больше воды на большей скорости будет звучать так «Да возможно, при небольшой разнице скоростей и маленькой выборке». Если перефразировать на нормальный язык: если идет несильный дождь с крупными и редкими каплями, и идти до укрытия не очень далеко, то итоговое промокание скорее будет зависеть от вашей удачи, нежели от вашей скорости.
Третий вопрос, «Как влияет размер капель на итоговый объем собранной воды при прочих равных условиях?».
Давайте перегруппируем таблицу, чтобы в третьем столбе были размеры капель, а во втором Катина скорость:
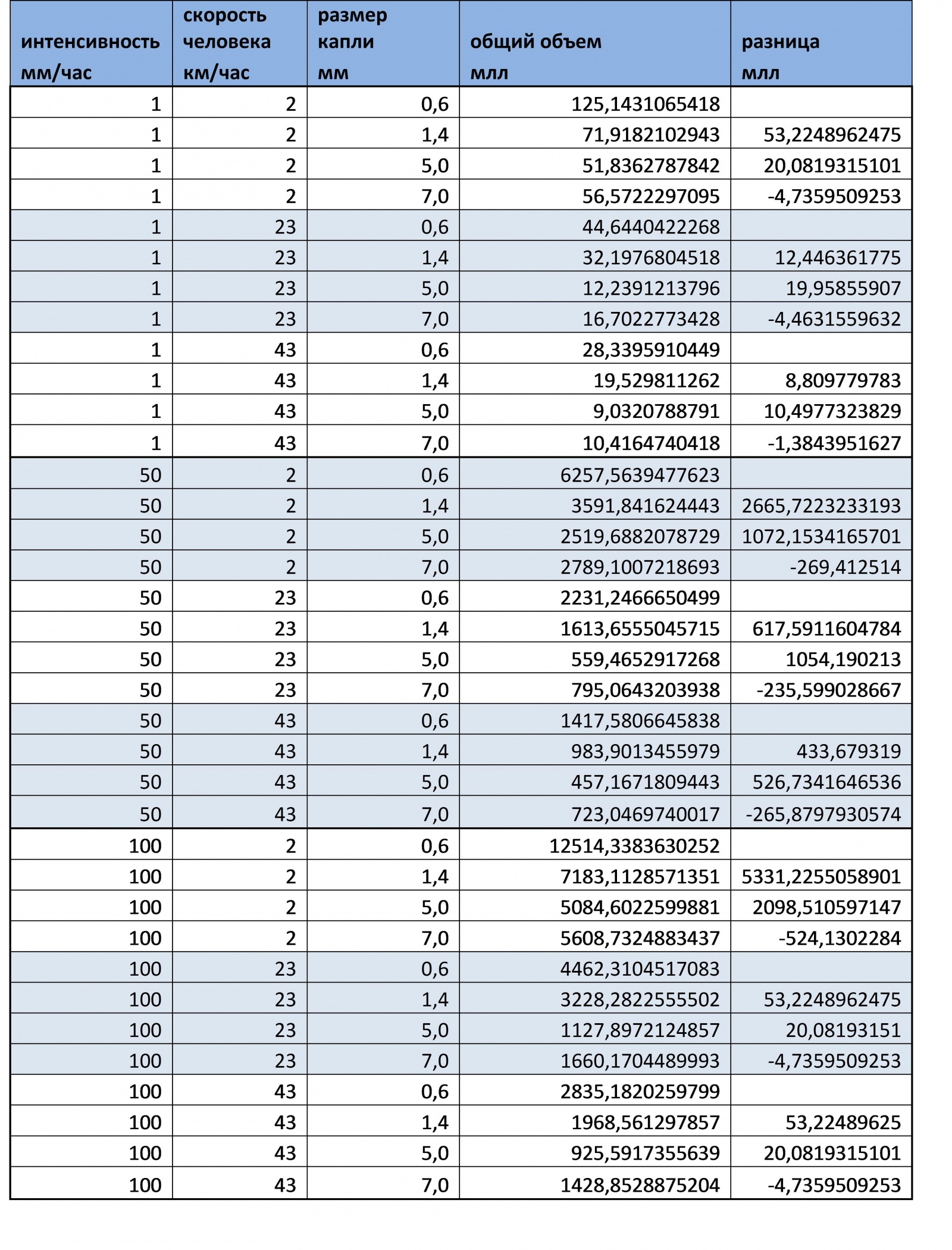
Как видно в диапазоне от 0.6 до 5 мм чем меньше объем капли, тем больше общий полученный объем воды, но в диапазоне 5 – 7 мм наоборот (с каплей размером 7 мм воды собирается больше, чем с каплей 5мм). Для поиска зависимостей в таблицу ниже добавлены столбцы с количеством капель в слое, скоростью падения капель, и количеством собранных капель всего за забег.
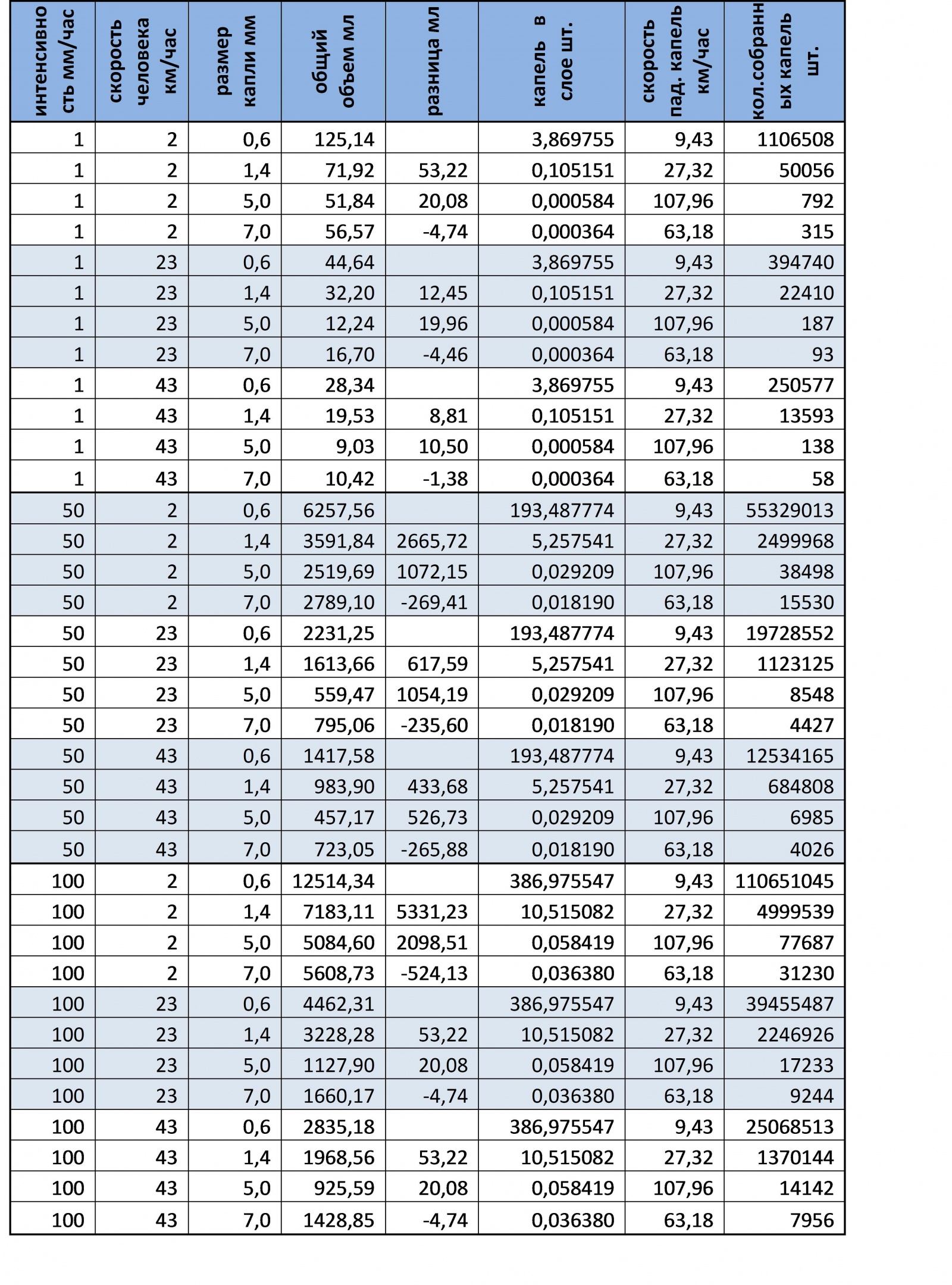
Как видно, объем собранной воды напрямую коррелирует только со скоростью падения капель – чем меньше скорость, тем больше объем собранной воды. Поскольку скорость является производной величиной, зависящей только от размера капли (в нашей модели), то ответ на третий вопрос может звучать так: При размере капель соответствующих минимальной скорости падения объем собранной воды будет максимальным, и наоборот, при размере капель соответствующих максимальной скорости общий собранный объем будет минимальным.
Однако здесь требуется уточнение – что будет, если одной и той же скорости соответствует несколько размеров капель.
Чтобы это проверить, пришлось провести дополнительную серию экспериментов на интенсивности 50мм/ч с изменением зависимости скорости от размера капли (а точнее трижды прибить гвоздями скорость падения). Вот, что получилось:
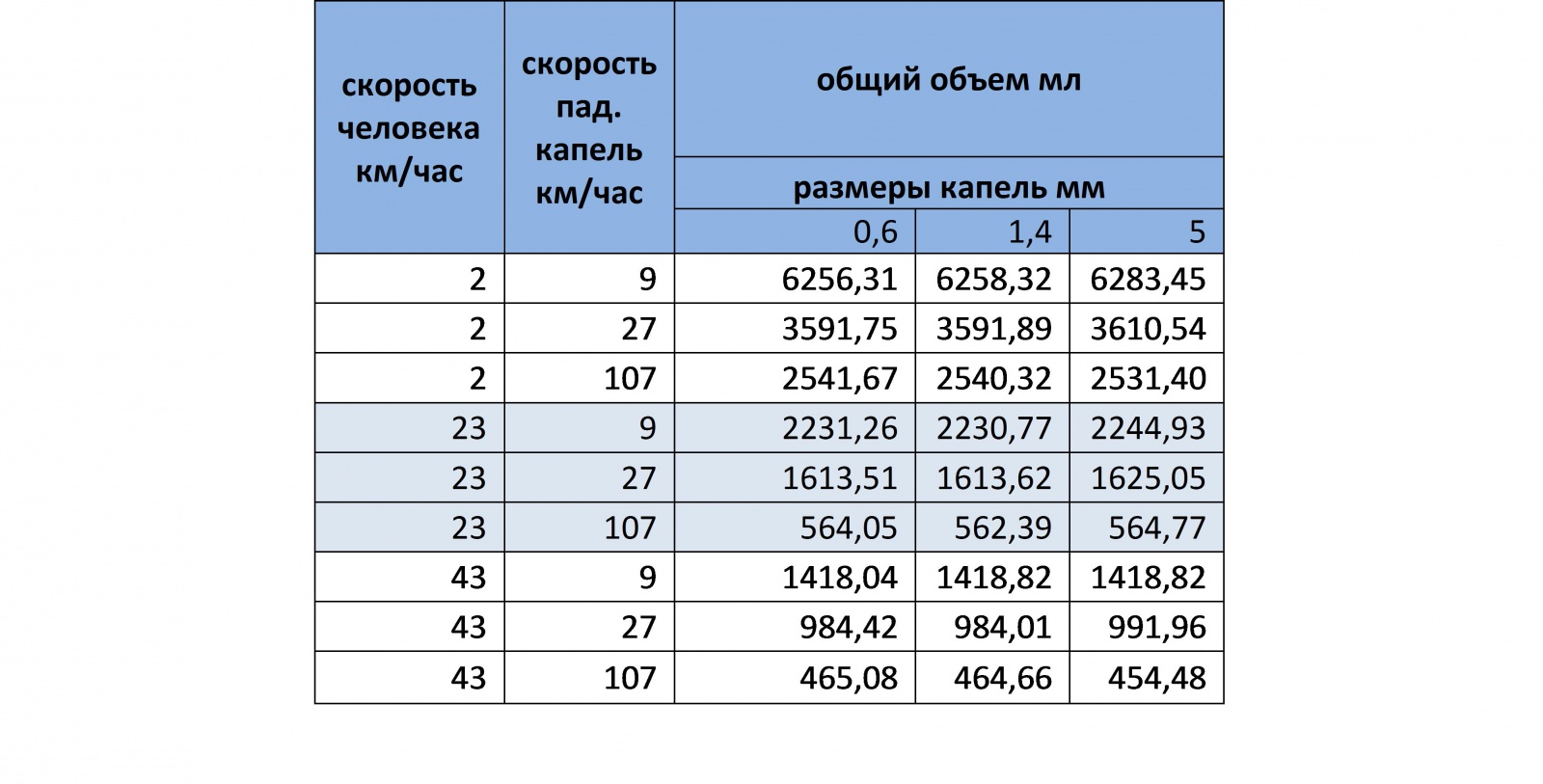
Как видно из таблицы, при прочих равных условиях, итоговый объем воды, собранной человеком зависит только от соотношения скорости человека и скорости падения капель, и не зависит от размера капли.
Выводы из этого наблюдения вряд ли имеют какую-либо практическую ценность, потому что здесь результаты сравниваются для строго определенных интенсивностей. В реальной мире, обычно увеличение размера капель и скорости их падения говорит об увеличении интенсивности. Другими словами, несмотря на эту красивую таблицу, если вас во время прогулки застанет ливень с крупными и быстрыми каплями, очень вероятно, что он промочит вас гораздо сильнее, чем обычный затяжной дождь с мелкими и медленными каплями потому, что интенсивность ливня будет гораздо сильнее.
Четвертый вопрос: «С какой стороны человек соберет больше воды – сверху, или спереди? От чего зависит это соотношение?».
В таблице ниже приведена наша изначальная группировка, опущен общий объем, но добавлены количества капель сверху, спереди, их соотношение и их общее количество.
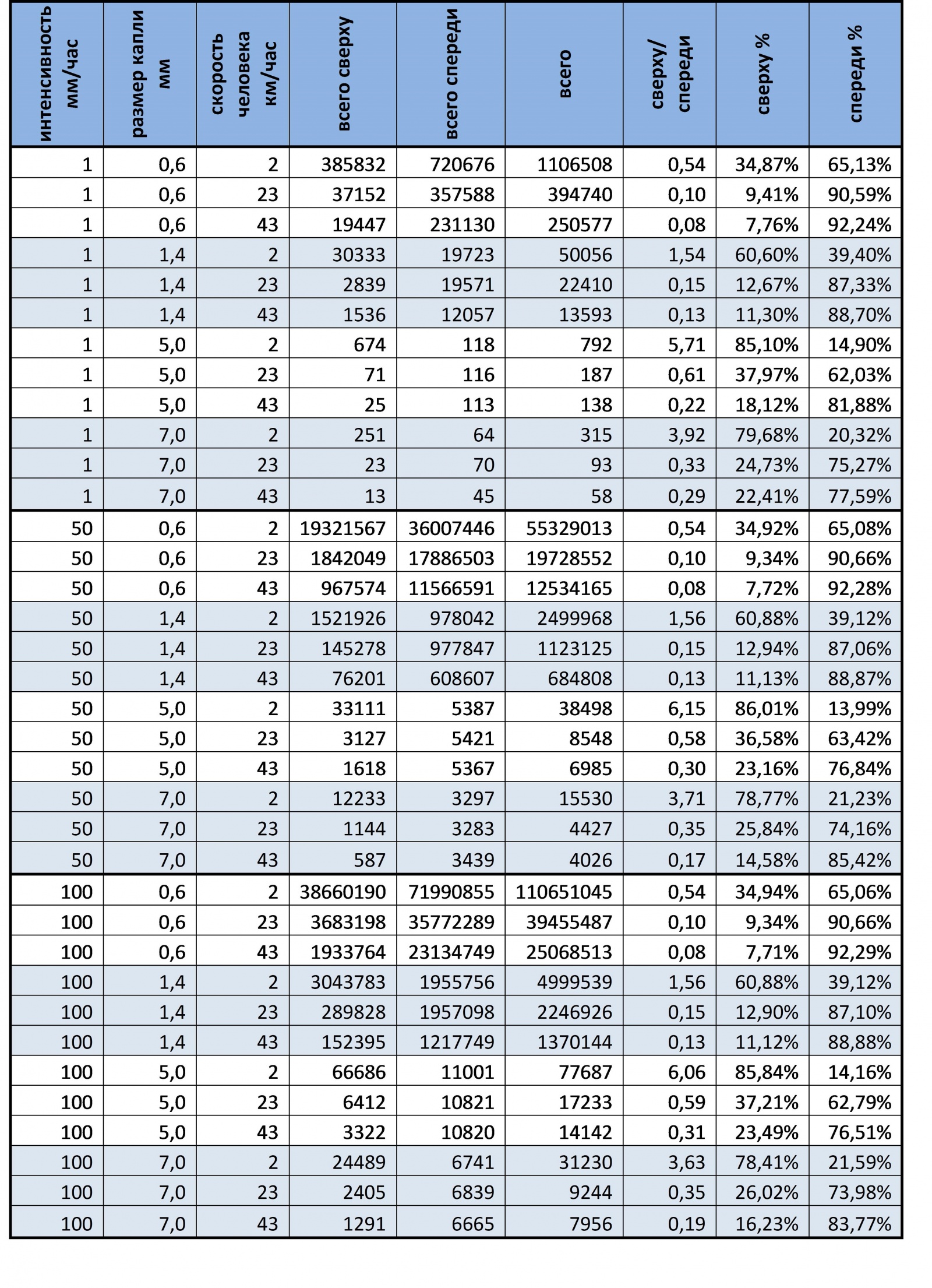
При анализе таблицы можно сделать несколько выводов, начну с наиболее очевидных:
1) Соотношение сильно зависит от скорости человека – чем медленнее движется человек, тем больше капель падает сверху (в каждом сете чем выше скорость тем меньше капель собранных сверху).
2) Если идти очень медленно, то независимо от того, какой идет дождь больше половины капель будет собранно сверху (абсолютно во всех сетах при скорости 2 км/ч количество капель полученных сверху больше 50 %).
3) Соотношение практически не зависит от интенсивности дождя, если сравнить соответствующие соотношения в суперсетах, то видно, что они отличаются совсем незначительно, или не отличаются вообще (таблица ниже).
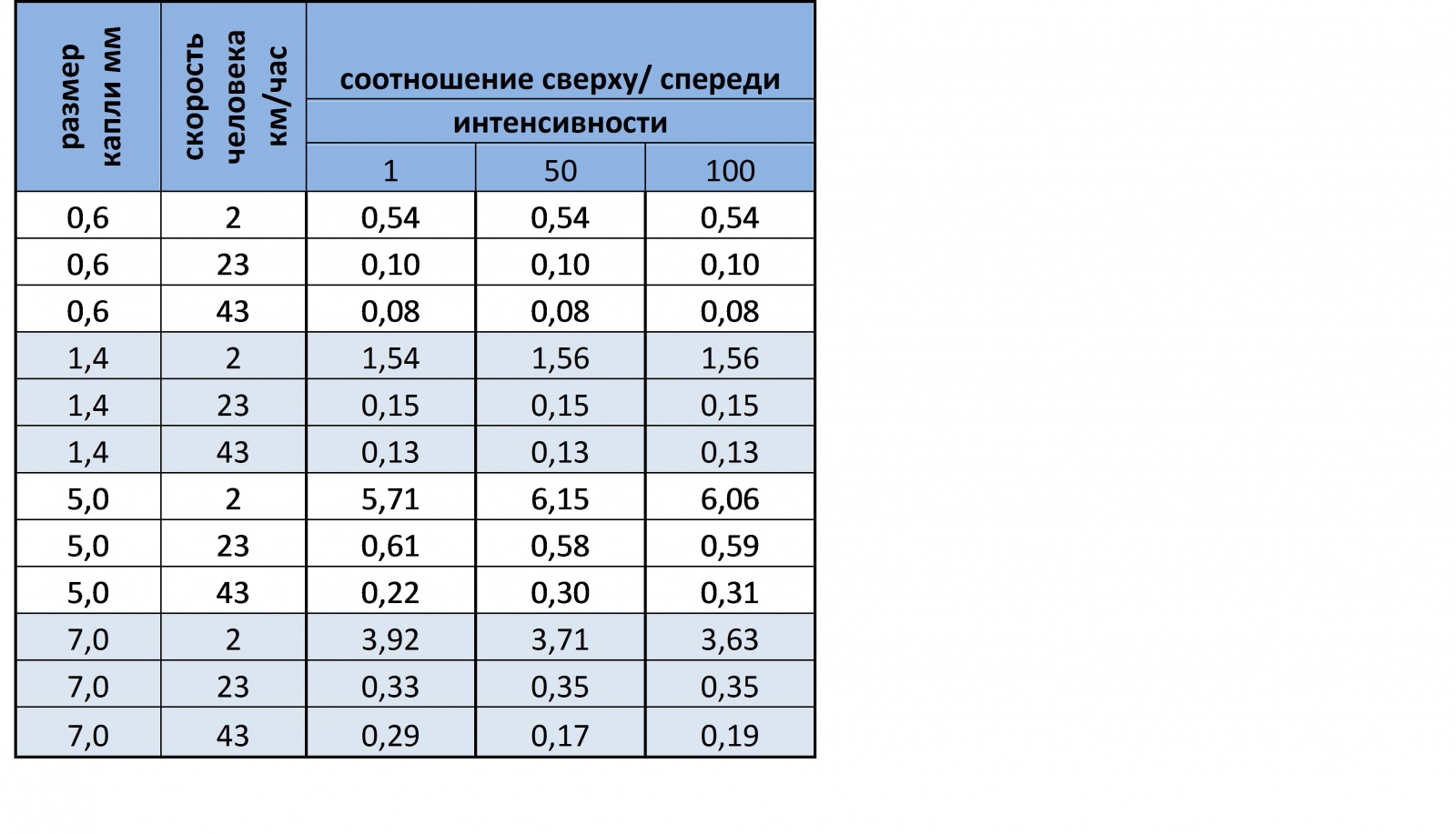
4) Соотношение сильно зависит не только от скорости Кати, но и от скорости падения капель. Если посмотреть на дельты значений соотношений с максимальной и минимальной скоростью Кати, то получиться что максимальный разброс соответствует размеру капли с максимальной скоростью падения (таблица ниже):
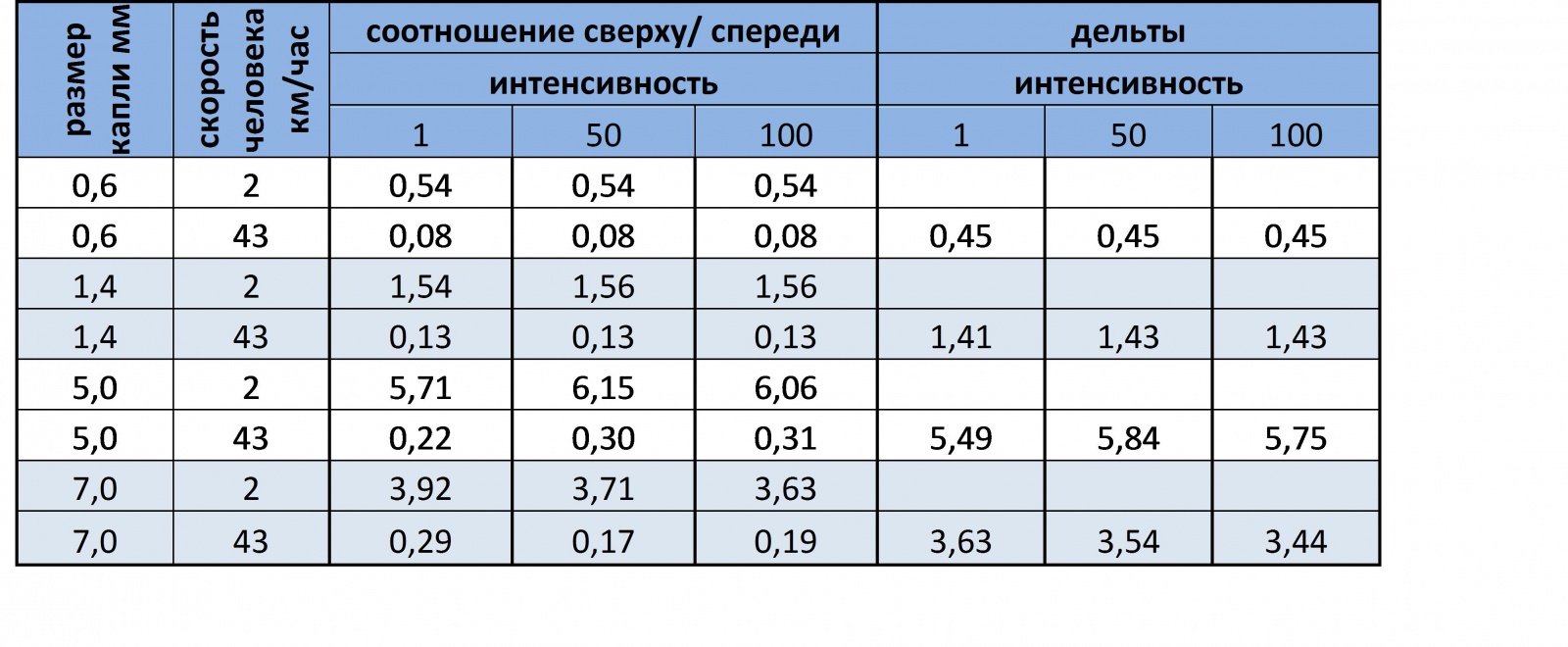
Это означает, что чем больше скорость падения капель, тем сильнее Катя может повлиять на итоговый объем собранной воды. Другими словами если вас застал ливень, который хлещет крупными каплями, то чем быстрее вы добежите до укрытия, тем меньше промокните. И наоборот, если на улице морось, множество мелких, висящих в воздухе капель, то бежать особого смысла нет, это не сильно повлияет на итоговый результат.
Таким образом, ответ на четвертый вопрос «С какой стороны человек соберет больше воды – сверху, или спереди? От чего зависит это соотношение?» звучит так: Человек, идя под дождем, может собрать больше воды как сверху, так и спереди, это соотношение, прежде всего, зависит от его скорости, но также большое влияние имеет скорость падения капель. Чем больше скорость человека, тем меньше капель упадет на него сверху.
На этом пожалуй, все. Как говорит доктор Скотт, палеонтолог, изучайте природу и делайте собственные открытия, ребята. :)
P.S. В тексте, в модели, в результатах, в поставленных вопросах и ответах на них, и в любых других местах могут быть ошибки, поэтому выкладываю проект в открытый доступ, если кто-то захочет проверить, перепроверить, повторить, дополнить, опровергнуть, ткнуть носом, и пр. – милости прошу github.com/sv-kopylov/raindrops-pub.git.
P.P.S Эта статья, является продолжением, теперь уже цикла статей про занимательное компьютерное моделирование, первая статья вот.
Автор: SergeyImber


